一种新型SIW传输线结构设计*

田伟成，汪晓光

0 引 言

基片集成波导（Substrate Integrated Waveguide，SIW）是一种可集成于介质基片中的传输线结构。通常，SIW是在介质基板上打两排金属通孔，再在基板两面覆以金属得到的。在满足一定条件下，将通孔阵列等效为金属壁，传输特性则可近似矩形波导分析。SIW结构具有低辐射、低插损、较高Q值、高功率容量、小型化和易于连接等优点。当电磁波在导波结构中传播时，会形成表面电流。目前，一般使用全波分析法和有限元法来对基片集成波导进行场分析，得出SIW各项参数和传统波导的等效公式。

1 传输线仿真与计算

SIW结构可以看作是一系列特殊的两边墙壁上细薄的插槽的矩形波导。横向切割这些电流的槽，将会带来大量的电流辐射。因为横向磁性场会产生纵向表面电流，所以存在纵向电流的TM模和存在横向磁场的TEmn(n≠0)是不能存在SIW结构中的。实验发现，如果引脚不焊接在一起的PCB金属板，SIW的参数属性将以非常显着的方式下降。因此，金属柱不仅起到屏蔽电磁波的作用，而且负责连接表面电流以保持导波传播。下面是通用的SIW与传统矩形波导的宽边的转换公式[1]：

其中，d为金属通孔的直径，s为相邻金属通孔孔间距，w为两行金属化通孔之间的距离。

本文通过在金属通孔内侧加入磁性圆柱，合理调节金属通孔和磁性圆柱的直径与间隙，使得SIW传输线的性能得到提高。所述两行磁性介质圆柱设置于两行金属通孔内侧并与其平行，各行磁性介质圆柱的中心线与同侧金属通孔中心线的行距相等，其距离为0.3～1.2 mm；各行磁性介质圆柱由相同的磁性介质圆柱等间距构成，如图1所示。

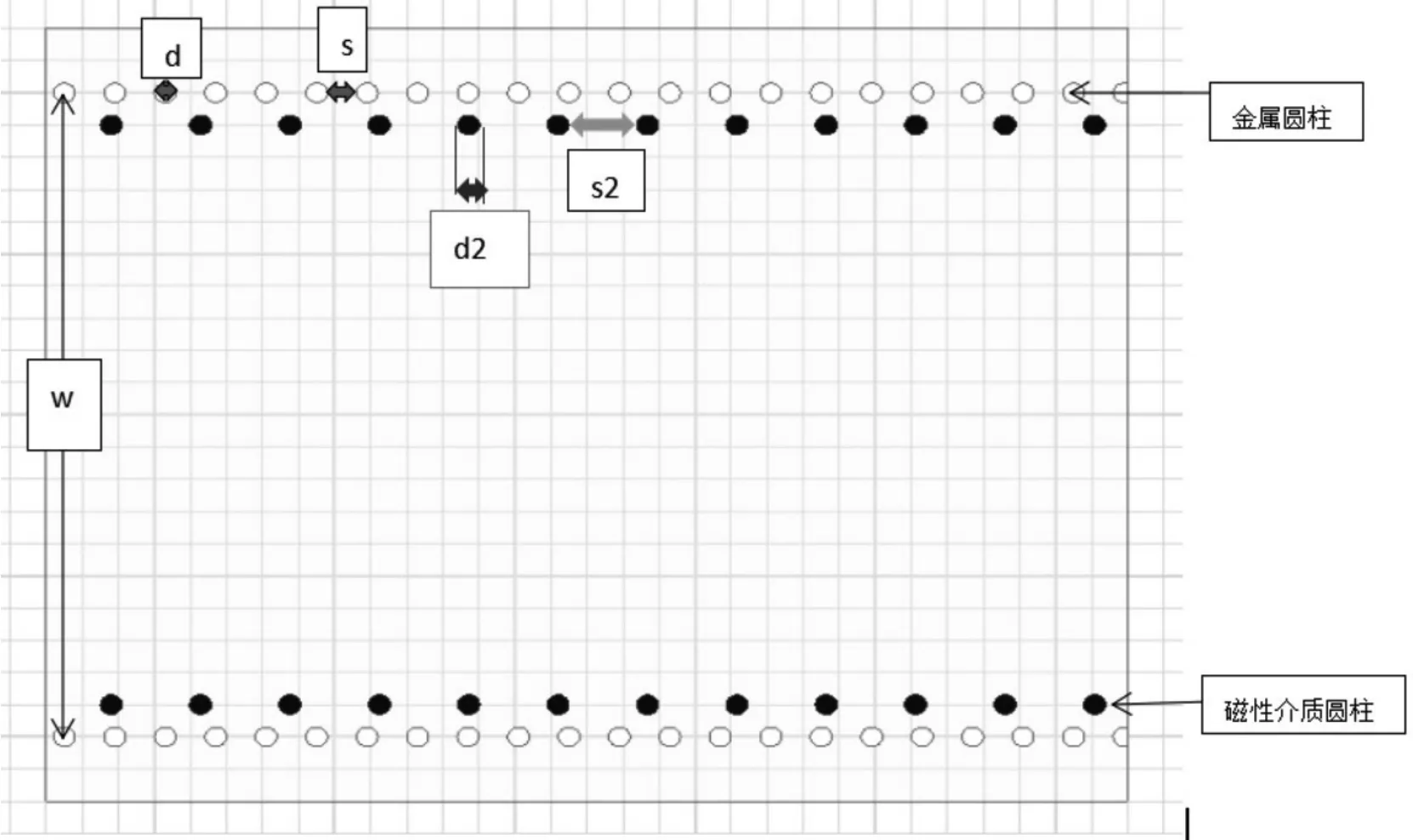
图1 本文SIW传输线结构

设计方法如下SIW经验公式（1）和本结构SIW经验公式s=2.5d-0.360 1，得到对应的中心频率和金属通孔的直径d、相邻金属通孔孔间距s和两行金属化通孔之间的距离w。

将磁性介质圆柱的直径d2、相邻圆柱间隙s2应用经验公式：d=1.133d2+0.04，s2=5.618d2+0.713 6；扫描磁性圆柱行与金属通孔行的最短距离，得到最优化尺寸；固定s、d、s2、d2这4个参数中的一个参数，并扫描其他参数得到最优的尺寸解。

2 入射与性能分析

众所周知，在SIW结构中，金属通孔的直径越小，金属通孔之间的间隙越小，SIW结构的参数性能越好。这不仅有利于散射特性、泄漏损失和带阻特性SIW结构，而且大大简化了设计流程，并使PCB设计更加紧凑。如图2所示[2]，电磁波在SIW结构中的传播方式与在传统矩形波导中的传播方式类似，电磁波通过在两个宽侧壁之间反射而在Z方向上传播。图3为电磁波入射金属通孔。通过几何关系可以得到[1]：

其中θ称为入射角，w为矩形波导的宽边宽度，n为电磁波模式阶数，λ为波长长度。虽然入射角不是直接可以表征的参数，但是衰减系数与入射角成反比例，从而影响SIW结构几乎所有的性能参数，如图4所示。

图2 电磁波在波导中传输

图3 电磁波入射金属通孔

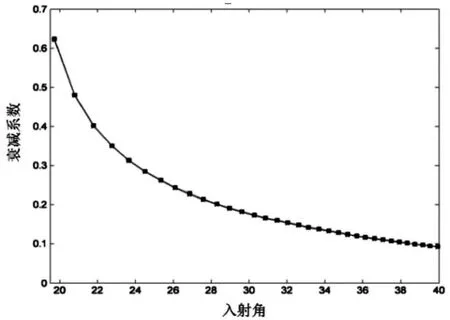
图4 衰减常数与入射角关系

当频率增加[3]时，如果入射角不变，电磁波的穿透性加强，会使得泄漏量增加。同时，入射角度会随着频率的增加升高，衰减系数又会变小。但是，在15°～50°时，该入射角对衰减系数的影响会大于频率对其的影响，特别是低频范围内的频率。模式顺序增加时，入射角度会减小，导致衰减系数增加，使得SIW结构性能变差。所以，对于SIW结构，入射角至关重要，一般选择大于或等于30°。磁性介质圆柱的加入，使得电磁波在传播时先经过磁性介质圆柱再入射到金属通孔，从而增大入射角，使得衰减系数减小。新型传输线的插损如图5所示，现有SIW结构损如图6所示，新型传输线的回波损耗如图7所示，现有SIW结构回波损耗如图8所示。可以看出，新型传输线插损和回波均优于现有SIW结构，提高了SIW结构的性能。

3 结 语

通过在传统SIW结构中紧靠两行金属通孔加入两行与其平行的磁性圆柱，形成新结构SIW传输线，从而实现在相同直径下插入损耗和回波损耗的性能优于现有SIW结构，且驻波比VSWR和传播常数保持不变。所述SIW传输线的设计方法中，SIW的经验公式为s=2.5d-0.360 1，新型传输线经验公式为d=1.133d2+0.04和s2=5.618d2+0.713 6。宽边宽度w则参考式（1）。需要说明的是，此类SIW传输线仅用于了X波段。

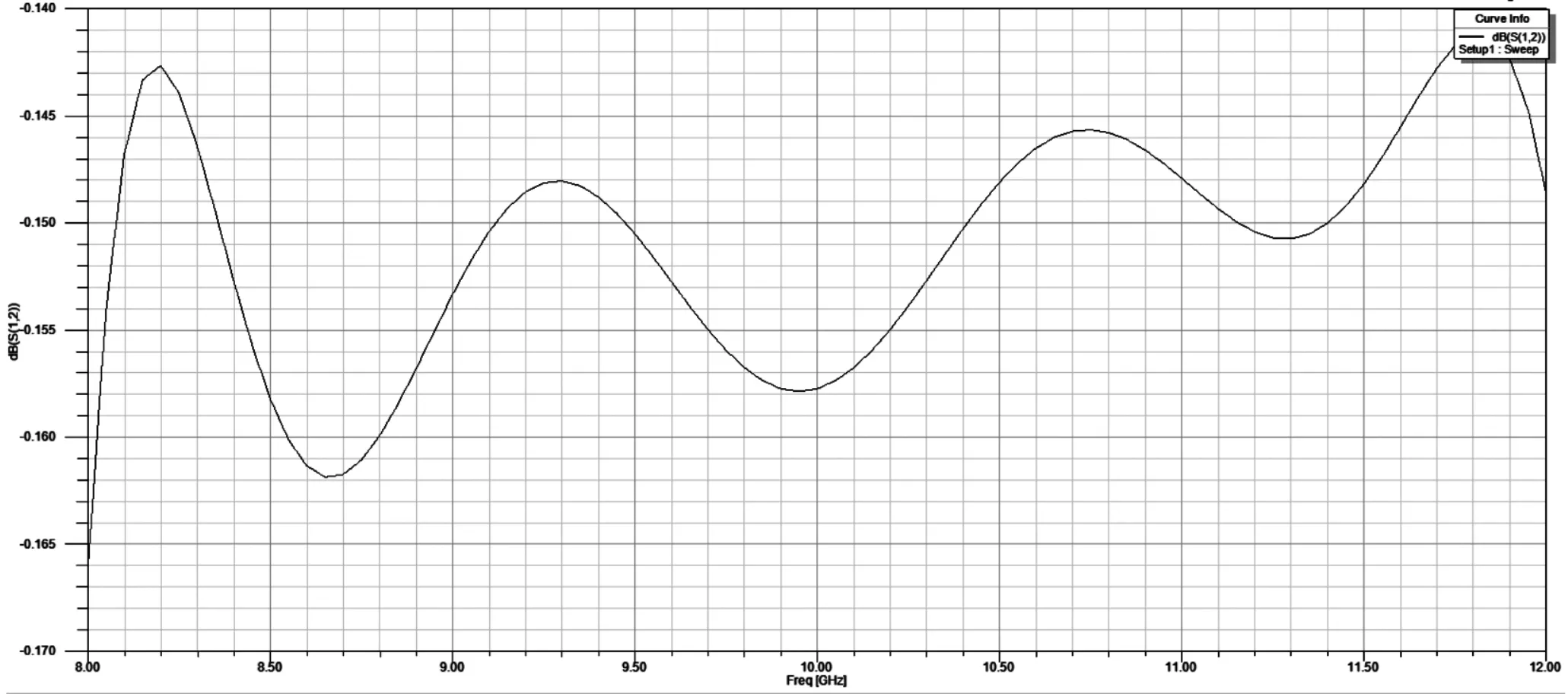
图5 本文S12参数仿真结果

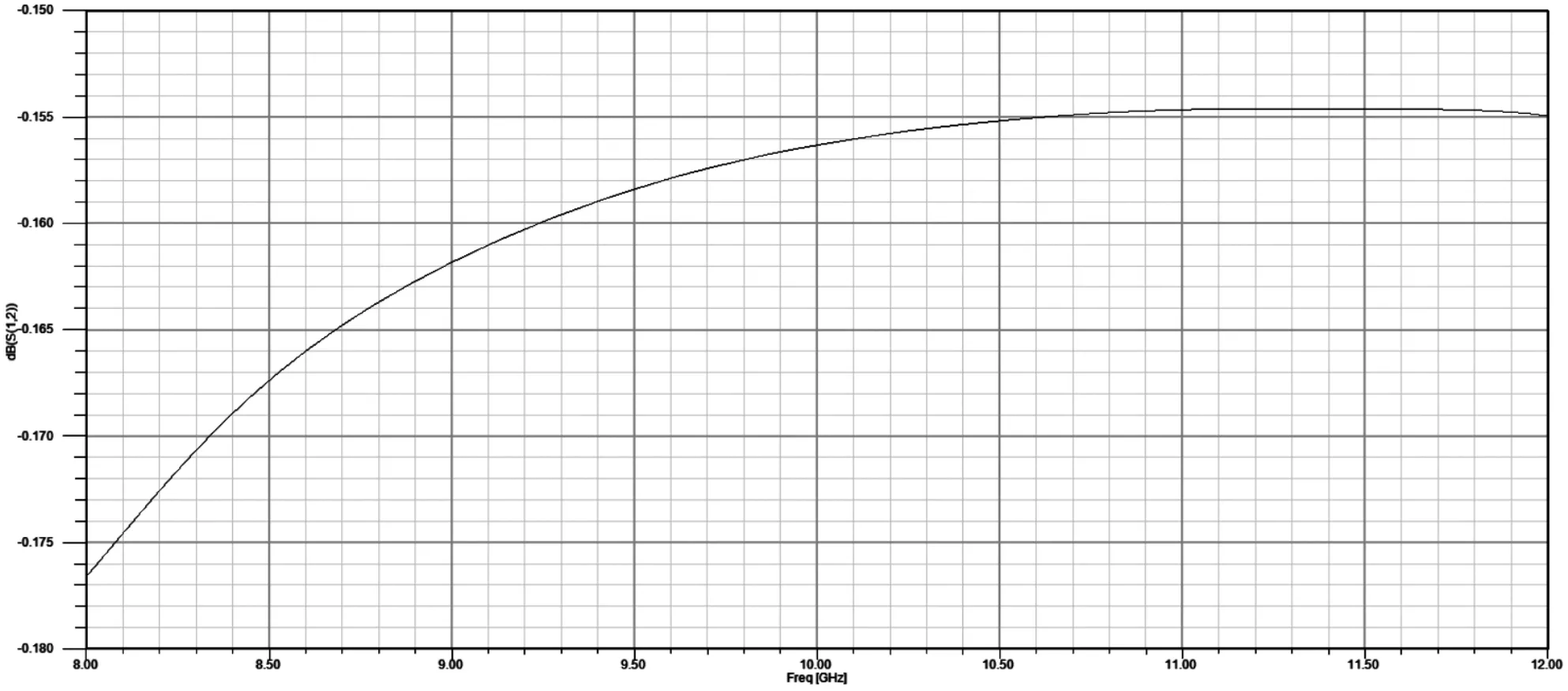
图6 相同条件下现有SIW传输线的S12仿真结果

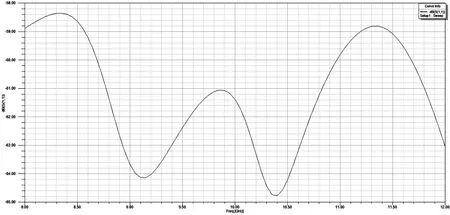
图7 本文S11参数仿真结果

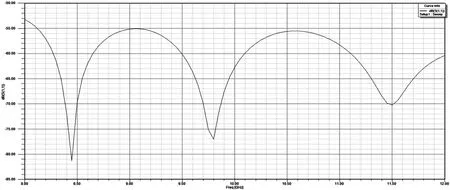
图8 相同条件下现有SIW传输线的S11仿真结果

[1] Xu F,Wu K.Guided-Wave and Leakage Characteristics of Substrate integrated waveguide[J].Microwave and Wireless Components Letters IEEE,2002,53(01):66-73.

[2] R.E.柯林.导波场论[M].上海:科学技术出版社,1966.Colin R E.Waveguide Theory[M].Shanghai:Science and Technology Press,1966.

[3] Zhu L,Wu K.Unified Equivalent-circuit Model of Planar Discontinuities Suitable for Field Theory-based CAD and Optimizationof M(H)MIC’s[J].IEEE Trans. Microw.Theory Tech.,1999,47(09):1589-1602.