加权马尔可夫模型在企业景气指数预测中的应用

王燕茹，王凯凯

（江南大学 商学院，江苏 无锡 214000）

0 引言

企业景气指数越来越受到各领域研究的重视，通过科学分析和预测指数未来波动变化，不仅可以从微观角度指导企业明晰行业趋势，预先提出应对解决策略；而且对于辅助国家统计部门科学准确地进行预测具有重要的宏观现实意义。因此，我国不仅将景气调查作为统计工作的一项重要内容，还将其作为判定整个经济景气状况的重要参数。

现有预测企业景气指数的方法并不丰富，根据目前参考文献，学术研究通常使用的预测算法和数学模型有：人工神经网络（ANN）、BP神经网络、粗糙集（RS）、遗传算法（GA）以及支持向量机（SVM）等。本文选用另外一种预测模型——加权马尔可夫模型对企业景气指数预测，并通过案例论证此模型的可行性和实用性。

1 加权马尔可夫模型

马尔可夫模型作为分析及预测未来趋势发展可能性的一种统计方法具有无后效性的特征。即序列是一个随机过程，且计算得到的各时刻所处的状态与时刻之前所处的状态无关。

马尔可夫链：假设存在概率空间(K，F，P )上的随机序列，其中设时间序列为，状态空间。如果对任意非负整数 1，m，k

并且式（1）左端要有意义，即假定：

不能为零，但在实际的应用过程中，通常情况下会令式（1）的右端：

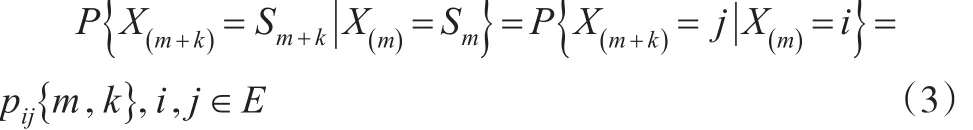
通常只考虑齐次，也就是对任意的m，k∈T，有：

式（4）中，pij(m，k)表示是在时间m时刻处于状态i，然后经过了k步状态转移到了状态 j的概率。同理，当m=1时，即 pij(k)表示为从状态i经过k步状态的转移，到达状态 j的概率，并且与初始的时刻无关。齐次的马氏链仅由初始状态分布以及状态转移概率矩阵决定。

加权马尔可夫模型的建立分以下几个步骤：

（1）确定指数分级标准。即为状态空间S，确定对应的状态值。

（2）计算各阶自相关系数。这里用rk表示相关系数。

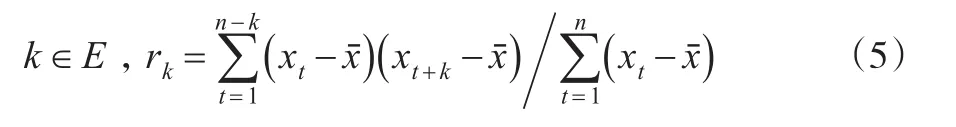
（3）归一化自相关系数。代表各滞时的马氏链权重，其中m是结合实际情况需要的最大阶数，一般取5。然后按照升序排列，建立不同的步长所对应的马氏链的状态转移概率矩阵。

（4）分别按照之前某季度的景气指数作为初始状态，再结合对应的状态转移概率矩阵便可以预测到未来某季度的状态概率值，其中i∈E ，k=1，2，…，m,k为滞时（即步长）。

（5）最后由不同滞时权重wk与每个状态的概率，求得加权和将预测概率归一化，计算状态特征值其中T为调整因子，这里取T为1。然后再将实际值纳入数据列，重复以上步骤，即可预测xi+1的企业景气指数。

（6）根据马氏链平稳分布、遍历性特点，进一步计算极限分布Pi，以及每个状态再现期Ti，其中

2 基于加权马尔可夫模型的企业景气指数预测

以北京市统计局统计年鉴提供的1999—2013年共60个季度的企业景气指数序列为例，分析并进行预测来说明此方法预测在实际具体应用中产生的效果情况。企业景气指数资料如表1所示。

表1 北京市1999—2013年60个季度企业景气指数序列以及对应的状态

下文主要分析此模型在实际应用中产生的效果是否与实际数据处在同一状态内，即是否准确实用以及误差率。首先以1999年第一季度至2013年第二季度共58个季度的景气指数预测2013年第三季度的指数。如果结果一致，再把2013年第三季度的实测数据资料加入以上序列中，然后预测2013年第四季度的指数状态。

（1）“马氏性”检验

在对数据序列进行建模预测前，需要先进行“马氏链”检验。一般采用χ2统计量检验。

设企业景气指数随机序列的分布状态处在m个状态，然后求得边际概率，得到一步状态转移矩阵边际概率。其中，当 n的数值充分大时，统计量χ2计算如式（7）所示。

根据所求得的以上两者所对应边际概率表以及统计量 χ2值，参照表2和表3的结果。

表2 边际概率值

表3 统计量计算值

结果表明，求得的统计量数值 χ2是74.2192，根据给定的显著性水平α取0.05，根据查表可得到分位点的数值。很显然，统计量值远大于分位点数值，因此可认为该企业景气指数序列具有“马氏性”。

（2）状态区间划分方法

在景气指数预测前期，指数状态确定是至关重要的环节。由于社会经济的复杂性，划分区间较为麻烦，其中涉及模糊理论的概念。参考文献中在确定指数状态等级时可以采用的方法主要有经验统计、有序聚类、模糊聚类、数理统计（3σ法）等，本文中运用数理统计法确定状态。

经过计算，该序列（1999年第一季度至2013年第四季度）的企业景气指数均值=130.34。根据国家统计局对企业景气指数具体划分的标准确定序列的级别，通常将序列划分成5个级别，对应马氏链的5个状态（见表4）。

表4 企业景气指数分级

依照表4中已确定的分级标准，将表1中的每个季度的景气指数状态对号入座，然后计算各阶自相关系数rw与不同步长时的马尔可夫链权重wk，结果如表5所示。

表5 各阶自相关系数与各个步长时的马尔可夫链的权重

（3）状态转移概率矩阵的计算

经过计算，可以求得不同步长的马尔可夫链的转移概率矩阵，取最大步长为5，即：

（4）计算预测值

依据1999年第一季度至2013年第二季度的企业景气指数以及对应的各步长的状态转移概率矩阵对2013年第三季度的景气指数所处的状态进行预测，预测步骤及结果如表6所示。

由表6可知，求得的状态特征值S=3.0089，这就可以说明2013年第三季度的企业景气指数处于状态3（较为景气），而实际调查统计的企业景气指数为126，也处于状态3（较为景气）区间，所以可以认为与实际情况基本符合。同理，将第三季度的实际值加入到资料序列中，预测2013年第四季度的企业景气指数所在的状态，预测结果见表7。

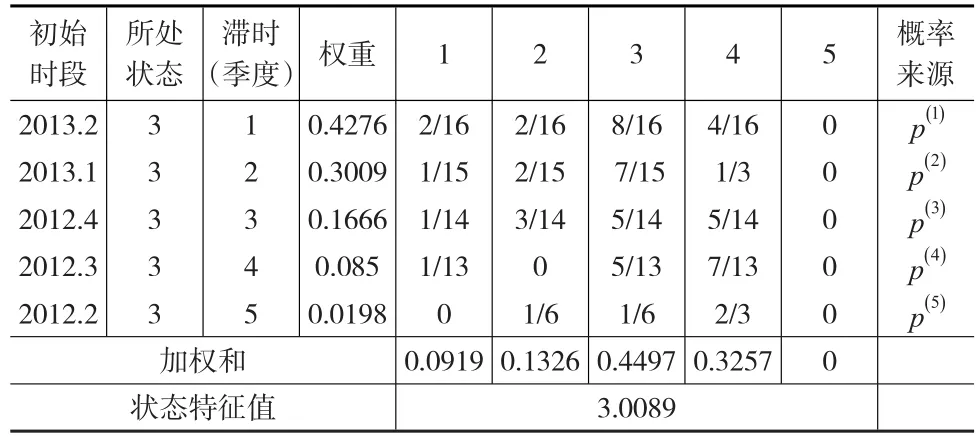
表6 2013年第三季度企业景气指数预测

表7 2013年第四季度企业景气指数预测

由表7求得的状态特征值S=3.0058，即预测的企业景气指数也是状态3（较为景气），并且2013年第四季度的实际景气指数为124.1，所以与实际情况基本上符合。这充分表明将加权马尔可夫这一模型应用于预测企业景气指数还是有效可行的。

（5）马尔可夫链的特征分析

最后根据马氏链具有的自身特征，对其进行分析：因为企业景气指数的5个状态之间是相通的，即i↔j(i≠j，且i，j∈I )，即遍历性；无周期规律，即非周期性的；可以构成完整的封闭集合，即状态空间，所以是不可约链。所有的状态之间在有限状态集合可以正常返，具有遍历性的特点，所以根据其遍历性的定理。在此可以计算极限分布，由以下给出的方程式组求极限分布：

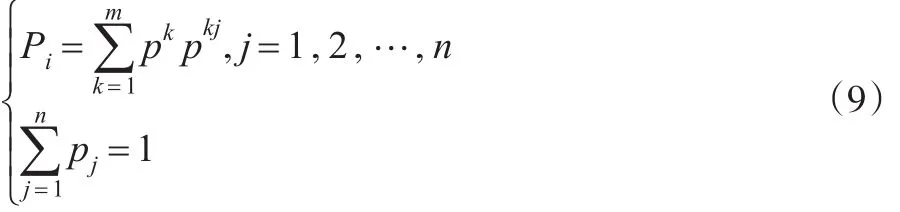
以步长为3（相依性最强）的马尔可夫链进行特征分析，应用式（9）可以求得极限分布值：p1=0.02837，p2=0.08780，p3=0.06134，p4=0.042066以及 p5=0.06730由极限分布便可求出每个状态的再现期；应用公式，每个状态的再现期为：T1=35.246，T2=11.389，

3 结论

本文通过近14年的企业景气指数统计结果可以看出，企业景气指数处在中度景气次数最多，平均2.377个季度出现一次，概率为0.42066，可能性最大；出现最少的是不景气区间，平均35.246个季度出现，概率为0.02837，可能性最小。

加权马尔可夫模型预测与实际结果几乎一致，但因为采用数学模型较为单一，预测结果仍存在不足和缺陷，预测过程不够全面深入，需要进一步完善数学模型。

（1）本文区间分级采用样本均方差法，该方法适合数据信息较大，使用范围广泛，计算简单方便。除此之外，还有有序聚类、模糊聚类等描述数值的变化区间，常用的有序聚类有Fisher算法等，至于哪种方法更优越，还有待深入研究。

（2）在今后的研究中，可以考虑加权马尔可夫模型与其他方法组合混合模型。比如支持向量机（SVM），基于SVM在数据挖掘和分类方面有良好的拟合能力，在时间序列预测被多次采用。还可以结合其他数学模型，比如ARMA模型、ANN模型、SCGM（1,1）模型、灰色模型、粗糙集等。综合各模型优势互补，寻找一种在企业景气指数预测最优的混合模型。

[1]Stock J H,Waston M W.A Procedure for Predicting Recessions With Leading Indicators:Econometric Issues and Recent Experience[J].NBER Working Paper,1993.

[2]Christian K,Karel M.Business Cycle Analysis and VARMA Models[J].Journal of Economic Dynamics and Control,2009,33(2).

[3]吴海民.BP人工神经网络在我国工业企业景气指数预测中的应用[J].兰州商学院学报，2007，23（2）.

[4]帅加琴.中国铜工业景气指数与预警系统研究[D].北京：北方工业大学硕士论文，2015.

[5]彭森.基于粗糙集与支持向量机的工业企业经济景气指数智能预测模型研究[D].武汉：华中科技大学硕士论文，2012.

[6]孙才志,张戈,林学钰.加权马尔可夫链在降水丰枯状况预测中的应用[J].系统工程理论与实践,2003，23（4）.

[7]姜翔程，陈森发.加权马尔可夫SCGM（1,1）c模型在农作物干旱受灾面积预测中的应用[J].系统工程理论与实践，2009，29（9）.