商品不可分割条件下价格变化时的消费者选择及其福利
夏 明
(南开大学 经济学院,天津 300071)
0 引言
消费者的选择和效用(福利)问题在微观经济理论中一直居于核心地位,很多微观经济理论和实证研究都是建立在消费者效用问题上。同时,微观经济理论又是宏观经济理论的基石,对消费者行为的考量在许多宏观经济模型的建立中是必不可少的。在诸多影响消费者行为的因素中,价格是最重要的因素之一,研究价格变化对消费者的行为和福利的影响对于制定各种科学合理的经济政策有着重要的意义。
在价格变化对消费者行为和福利的影响方面,学者们进行了深入的研究[1-4],国内比较有代表性的研究主要集中在粮食和食品上:邵飞等(2010)[5]、徐永金等(2012)[6]和苗珊珊(2014)[7]均运用Minot模型分别分析了我国玉米价格波动的福利效应、粮食价格波动对主产区福利的影响和中国粮食价格波动的农户福利效应;罗知等(2010)[8]研究了进口商品价格波动对城镇居民消费支出的影响;赵昕东等(2013)[9]利用QUAIDS模型和补偿变量法分析了食品价格上涨对不同收入等级城镇家庭消费行为与福利的影响;李光泗等(2014)[10]用供求曲线图以及剩余的概念分析了两种不同粮食价格政策对社会福利的影响;王小叶(2015)[11]从希克斯消费者剩余的角度研究了食品价格上涨对城镇居民福利的影响;赵昕东等(2016)[12]运用EASI需求系统分析了各类食品价格上涨对不同收入等级城镇家庭消费与福利的影响。但这些研究所基于的单个消费者需求曲线和市场需求曲线是以商品在实物上可无限分割(这就使得商品的数量可以是任意的非整数)为假设条件的。而在现实生活中,商品在实物上作为一个完整的个体一般是不可分割的,只能以整数单位被购买,如商品房、汽车、家电产品、服装等;而有些商品,其本身虽可被分割或近乎无限分割,但由于早已被包装成了一份一份的,因此也只能以整数单位(份数)被购买,如矿泉水、各种饮料、食用油、奶粉、麦片、超市里已被分割并包装好的肉类等。因此,需要研究在现实中商品不可分割条件下当商品价格变化时消费者的最优选择是如何确定的,呈现怎样的规律和特征,相应的消费者福利又是怎样的。而对于这些问题,鲜有学者进行过研究,因此,本文将基于柯布-道格拉斯效用函数对这些问题进行研究。
1 模型构建
为了使分析具有最广泛的代表性,本文的分析基于最常用的柯布-道格拉斯效用函数,这一函数形式是最典型的良性且严格凸的偏好形式。在柯布-道格拉斯效用函数形式下,所分析的商品是正常商品,这就排除了低档商品和吉芬商品这些特殊情况。同时,模型中的消费者定义为代表性消费者。
在确定了效用函数形式之后,依照对消费者最优选择问题的经典分析,本文设有两种商品:一种是我们所要关注的商品,而另一种是所有其他商品的复合,称为复合商品,通常视为货币。这样既可以简化分析,又不失结论的一般性,由此可构建一个二维图形模型,如图1所示:
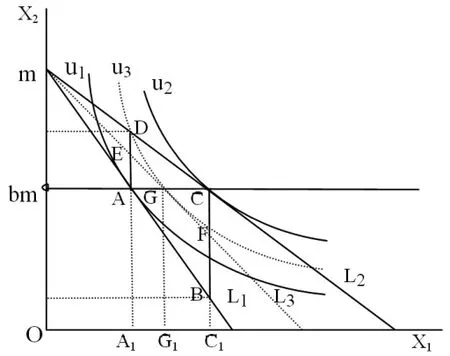
图1
图1中,横轴代表商品1的数量,记为X1,这是我们要关注的商品,其价格记为P1;纵轴代表商品2的数量,记为X2,商品2是除商品1之外的所有商品的复合,称为复合商品,其价格记为P2。由于把复合商品视为货币,因此有P2=1,同时,由于最小单位的货币可以很小,因此可以把商品2近似看成可无限分割。
模型中的柯布-道格拉斯效用函数形式是U=X1a
X2b,其中U代表效用,系数a和b分别是商品1和商品2的消费支出所占的收入份额,且有a+b=1。图1中的两条无差异曲线u1和u2代表不同的效用,且有u2>u1。
图1中的L1和L2分别是当商品1的价格P1为P11和P12(P11>P12)时的预算线,L1的方程是 P11X1+P2X2=m ,L2的方程是 P12X1+P2X2=m 。L1与u1相切于点A,L2与u2相切于点C,点A与C所对应的X1分别是A1和C1,设A1和C1恰为相邻的两个整数,即C1=A1+1。在柯布-道格拉斯效用函数形式下易解出:A1=am/P11,C1=am/P12。
图1中的D点是位于L2上的一点,D点所对应的X1也是A1,连接A、D两点,则线段是与横轴垂直的,上的点所对应的X1均为整数A1;B点是位于L1上的一点,B点所对应的X1也是C1(B点也有可能位于L1在横轴下方的延长线上,即预算线为L1时,全部的收入都不足以购买到C1单位的商品1。但为了分析的方便,本文假设B点位于横轴上方,这样做并不失分析和结论的一般性),连接B、C两点,则线段是与横轴垂直的,上的点所对应的X1均为整数 C1。
2 消费者最优选择分析
当价格变化时,在商品可无限分割的条件下,消费者的最优选择轨迹是一条连续的价格提供曲线。而在商品不可分割,只能以整数单位被选择或购买的实际条件下,消费者的最优选择是怎样的呢?现以图1中区间(A1,C1)即价格区间(P12,P11)为例进行分析。
当P1处于区间(P12,P11)时,相应的预算线就处在L1与L之间,如图1中的虚线L所示。L与线段和分
233别相交于点E和F,与价格提供曲线相交于点G,点G所对应的 X1为 G1,且 A1<G1<C1,G1是一个非整数。在商品可无限分割条件下,G是一个最优选择,消费者会选择购买数量为G1的商品1。但是当商品不可分割时,G1是无法实现的,从而G也是不可实现的,那么此时的最优选择是怎样的呢?当商品不可分割,只能以整数单位被购买时,消费者只能在自己的预算线上所对应的X1为整数的点中去选择使其效用最大的点。那么如何才能最为方便地找到这些点呢?更为重要的,这些点的分布具有怎样的规律和特征呢?
图1中的G点是L3与位于u1和u2之间的某条无差异曲线(如图中的虚线u3)的切点。根据边际替代率递减的原理,从G点出发,沿着预算线L3向左上方移动。即随着X1越来越少时,每减少一单位X1,为保持效用不变,需增加的X2的量应当越来越多,即ΔX2/ΔX1的值应当越来越大于G点处的边际替代率(即预算线L3的斜率P1)。而由于预算线L3的斜率不变,恒等于P1,每减少一单位X1,增加的X2的量也是固定不变的,即固定为P1,因此,从G点出发,沿着预算线L3向左上方,其效用是越来越少的。所以,在L3上,位于G点左边的所有对应的X1为整数的点中,效用最大的一定是G点左边第一个这样的点,即E点。由于L3代表位于L1与L2之间的任一条预算线,则L3与价格提供曲线的交点即G点就是价格提供曲线上位于A点与C点之间的任一点,因此L与线段的交点即E点就是位于线段
3上A点和D点之间的任一点。同时,当P1=P11或P12时,则L3与L1或L2重合,G点就分别与A点或C点重合,则E点就分别与A点或D点重合,因此,E点将取遍线段上所有的点,即E点所对应的X1总是为整数A1。同样根据边际替代率递减的原理,在L3上,位于G点右边的所有对应的X1为整数的点中,效用最大的一定是G点右边第一个这样的点,即F点。同理可知,F点将取遍线段上所有的点,即F点所对应的X1总是为整数C1。
因此,当价格P1在区间[P12,P11]上变化时,相应的预算线就在L1与L2之间变动(包括与L1、L2重合的情况),相应的最优选择点G就在价格提供曲线上,在点A与点C之间变动(包括与点A、C重合的情况);对应的G1将相应的在区间[A1,C1]上变动。在商品不可分割的条件下,最优选择要么是点G左边的线段上的点(包括G点与A点重合的情况),要么是G点右边的线段上的点(包括G点与C点重合的情况);相应的对X1的最优选择要么是小于或等于G1的最大的整数A1,要么是大于或等于G1的最小的整数C1。那么什么时候选择线段上的点(即点E,这时X1=A1),什么时候选择线段上的点(即点F,这时X1=C1)呢?
随着价格P1的变化,每一条相应的预算线L3都将与线段、分别交于E、F点,因此可先求出E、F点的坐标,然后得出点E、F处的效用(分别记为UE、UF)。
先求出E点的坐标。E点是L3与线段的交点,因此可由下列方程组解出E点的坐标:

其中的bm和m-A1P12分别是点A与点D的纵坐标。
解得E点的横、纵坐标分别为X1=A1和X2=m-A1P1,(P12≤P1≤P11)。则P11),可见UE是相对应的价格P1的函数。
同理,根据下列方程组解出F点的坐标:

其中的m-C1P11和bm分别是点B、C的纵坐标。
解得F点的横、纵坐标分别为X1=C1和X2=m-C1P1,则P11),可见UF是相对应的价格P1的函数。
容易证明,UE和UF均是连续可导且在定义域(P12≤P1≤P11)内均是单调递减的,反过来说,当P1从P11逐渐下降到P12的过程中,UE和UF均是逐渐增大的。同时,由于A点的效用大于B点的效用,而D点的效用却又小于C点的效用,也就是说当P1=P11时,UE>UF。而当P1=P12时,UE<UF,那么在P1从P11逐渐变化到P12的过程中,必有某个价格使得UE=UF。求解方程UE=UF,可得:
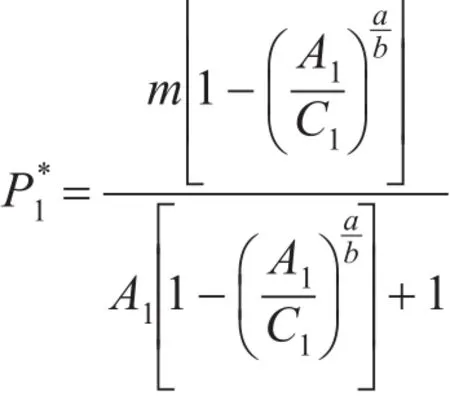
如将A1=am/P11,C1=am/P12代入上式,还可得:

也可以通过图形来看,假设图1中所画出的L3恰好是当P1=时的预算线,那么图中的点E、F处的效用是相等的,UE=UF。即不管选择的X1是A1还是C1,效用都一样,都是最优选择;而当<P1≤P11时,图中线段(除去端点E)上的点的效用均大于线段(除去端点F)上相应点(即处于同一条预算线上的点)的效用。此时应取线段(除去端点E),即选择的X1为A1;同理,当P12≤P1<时,应取线段(除去端点F),即选择的X1为C1。由此可知,在商品不可分割的条件下,消费者的选择具有这样的特征:即消费者会在与非整数最优选择量(在商品可无限分割假设下所得出的,如图1中的G1)最左右相邻的两个整数量(如图1中的A1和C1)之间作出选择。随着价格的下降,消费者最初会一直选择位于该非整数最优选择量最左边的整数量(即小于该非整数最优选择量的最大整数量);当价格下降突破某个临界值(如上述中的)时,消费者的选择会跃升到位于该非整数最优选择量最右边的整数量(即大于该非整数最优选择量的最小整数量)。
以上是以某两个相邻整数量(A1和C1)为端点所构造的区间为例进行分析,而对于所有这样的区间都可以有同样的分析和结论。可见,在商品不可分割的条件下,随着价格的逐渐变化,消费者的最优选择的轨迹不再是一条连续的价格提供曲线,而是由一系列所对应的商品数量恰为整数的垂直线段所组成。
3 消费者福利分析
现从效用的角度来分析消费者的福利,以图1中区间[A1,C1]为例。
本文假设图1中所画出的L3即为P1=时的预算线,则点E、F处的效用相等。L3与价格提供曲线相交于点G,点G所对应的X1为G1,本文先分析区间[A1,G1],再分析区间[G1,C1]。
在区间[A1,G1]上,即价格区间[,P11]上,与每一个价格对应的预算线与线段和各有一个交点,线段上的交点的效用(记为uAG)是大于线段上的交点的效用(记为uAE),在商品不可分割的条件下,只能取线段上的交点,由此就产生了效用损失。而在价格从P11逐渐下降到的过程中,相应的预算线就会逐渐地从L1转向L3,相应的预算线与线段的交点会逐渐地从点A移向点E,与线段----的交点会逐渐地从点A移向点G,因此就会连续产生效用损失,则总效用损失就可用以下数学式来计算:
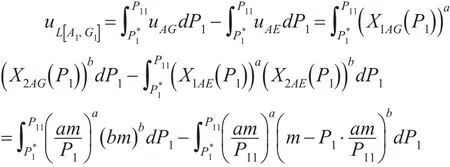
求解上式得:

同理,对于区间[G1,C1],即价格区间[P12,],其总效用损失可用以下数学式来计算:
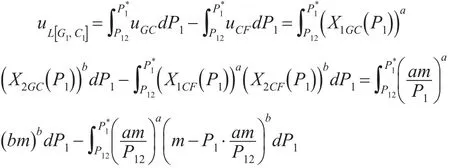
求解上式得:

上面分别求出了区间[A1,G1]和[G1,C1]上的效用损失,则区间[A1,C1]上的效用损失就是和之和,即便是区间[A1,C1]上消费者的福利损失。
以上是以某两个相邻整数量(A1和C1)为端点所构造的区间为例进行分析和计算,而对于所有这样的区间上的福利损失都可以有同样的分析和计算。
4 总结
本文是以柯布-道格拉斯效用函数这一偏好形式为例进行分析。实际上,对于其他良性且严格凸的效用函数形式,只要所涉及的商品(即文中的商品1)是非吉芬商品,哪怕是低档商品,其需求量都会随着价格的下降而增加。本文的分析和结论也是完全适用的,仅仅是所计算出来的效用损失的表达式不同(因为效用函数的具体形式不一样)。
本文基于柯布-道格拉斯效用函数对商品不可分割条件下当价格变化时的消费者最优选择及其福利进行了分析。结果表明,在商品不可分割条件下,由于消费者只能以整数单位去选择或购买商品,因此随着价格的逐渐变化,消费者的最优选择的轨迹不再是一条连续的价格提供曲线,而是由一系列的所对应的商品数量恰为整数的垂直线段所组成。这同时也会导致消费者对商品的选择不是过少就是过多,进而就会导致福利的损失。因此,为了减少消费者的福利损失,可以采取一些措施对商品进行尽可能的分割或者“分割”,这方面的措施可以包括两种情况:一是对于那些在实物上可进行一定程度分割的商品,在综合考虑了各种因素(比如分割商品所导致的成本)的情况下可尽量分割;二是对于那些在实物上不能进行分割的商品,可以采用产品差别化的办法对其进行“分割”。
[1]Ackah C,Appleton S.Food Price Changes and Consumer Welfare in Ghana in the 1990s[R].CREDIT Research Paper,2007.
[2]Leyaro V,Morrissey O,Owens T.Food Prices,Tax Reforms and Consum⁃er Welfare in Tanzania 1991—2007[J].International Tax and Public Finance,2010,17(4).
[3]Azzam A M,Rettab B.A Welfare Measure of Consumer Vulnerability to Rising Prices of Food Imports in the UAE[J].Food Policy,2012,37(5).
[4]Song Z,Li L,Ma C.The EASI Demand System:Evidence From China Household[R].MPRA Paper NO.48435,2013.
[5]邵飞,陆迁.我国玉米价格波动福利效应分析[J].价格理论与实践,2010,(8).
[6]徐永金,陆迁.粮食价格波动对主产区福利影响的实证分析[J].财贸研究,2012,(5).
[7]苗珊珊.中国粮食价格波动的农户福利效应研究[J].资源科学,2014,(2).
[8]罗知,郭熙保.进口商品价格波动对城镇居民消费支出的影响[J].经济研究,2010,(12).
[9]赵昕东,汪勇.食品价格上涨对不同收入等级城镇居民消费行为与福利的影响——基于QUAIDS模型的研究[J].中国软科学,2013,(8).
[10]李光泗,郑毓盛.粮食价格调控、制度成本与社会福利变化——基于两种价格政策的分析[J].农业经济问题,2014,(8).
[11]王小叶.食品价格上涨的成因与对城镇居民福利的影响研究[D].泉州:华侨大学硕士论文,2015.
[12]赵昕东,王小叶.食品价格上涨对城镇家庭消费与福利影响研究——基于EASI模型[J].财经研究,2016,(3).

