广义有序加权指数调和平均算子及其应用

何 霞，刘卫锋

（郑州航空工业管理学院 理学院，郑州 450015）

0 引言

集成算子的研究是多属性决策的一个核心问题，目前，人们提出了许多有效的集成算子用于决策信息集成，诸如WA算子[1]、WG算子[2]、OWA算子[3]、OWG算子[4]、OWH算子[5]、GOWA算子[6]、Bonferroni平均算子[7]、Heronian平均算子[8]等，而且逐渐形成了以研究集成算子的性质、分类、构造等为内容的集成算子理论。

在集成算子的构造方面，Yager[9]和Calvo[10]等首先从理论上探讨了集成算子与罚函数之间的关系，证明了一些常见的集成算子的确可以通过罚函数而得到的,为研究集成算子的构造开辟了一条新途径。随后，Calvo和Beliakov等[11]从一般意义上说明了通过罚函数来构造集成算子的条件，并探讨了罚函数与集成算子之间的联系。Zhou等通过构造不同的罚函数，得到了多种广义集成算子，如GOWLW 算子[12]、GOWEP 算子[13]、GOWLP 算子[14]、GOWM算子[15]、GOWP算子[16]以及GOWLH算子[17]等，这些算子丰富了现有集成算子的类型，也对人们构造更多类型的集成算子发挥着积极地启发作用。

在上述研究基础上，本文继续利用罚函数的思想来构建一个广义集成算子，并研究其决策应用。首先，根据集成数据和集成结果之间的偏差构建并求解一个基于罚函数的最小化优化模型，从而定义了广义有序加权指数调和平均算子(GOWEHA)，并研究了该算子的性质。然后，定义了GOWEHA算子的orness测度，探讨了orness测度的性质，并在给定orness水平下，提出了求解GOWEHA算子权重向量的最小指数平方法。最后，提出了一种结合GOWEHA算子的多属性决策方法，通过实例说明方法的可行性。

1 相关概念

为方便起见,约定 I=[0，1]。

定义1[3]:设 a1，a2，…，an∈I为待集成数据，若函数：

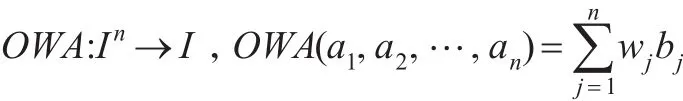
则称OWA为有序加权平均算子，简称为OWA算子，其中 bj为 ai中第 j大的数，权重向量为 w=(w1，w2，…，wn)，且

定义2[3]：OWA算子的orness测度定义为orness(w)

定义3[6]：设 a1，a2，…，an∈I为待集成数据，若函数：

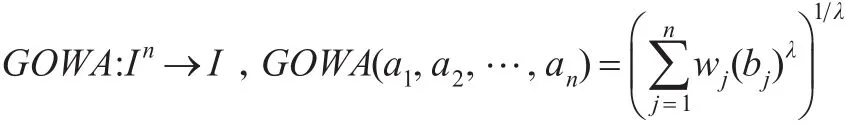
则称GOWA为广义有序加权平均算子，简称为GOWA算子，其中bj为ai中第 j大的数，权重向量为w=(w1，w2，…，wn)，且，参数 λ∈ R-{0}。

定义4[6]：GOWA算子的orness测度定义为

定义5[9-11]：若函数P:In+1→I满足下面三个条件:

（1）任意向量 x∈In和数 y∈I，有 P(x，y)≥0；

（2）若 x=y且 y=(y，y，…，y)∈In，则有 P(x，y)=0；

（3）对每个固定的向量x，使得P(x，y)的最小值构成的集合是单点集或区间；

则称函数P为一个罚函数。

2 GOWEHA算子

2.1GOWEHA算子的定义

设 a1，a2，…，an为待集成数据，w=(w1，w2，…，wn)为数据加权向量，且。若集成结果为n元函数 y=f(a1，a2，…，an)，则希望集成数据aj与集成结果 y之间的偏差越小越好，为此构造罚函数J和最小化问题：

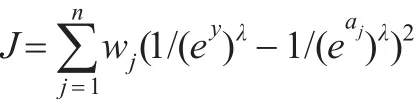
其中，λ为参数，且λ∈R-{0}。

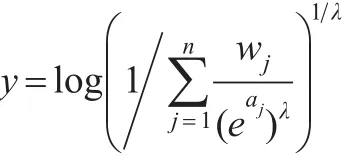
根据上式，可以定义广义加权指数调和平均算子。

定义6：设 a1，a2，…，an∈I为待集成数据，若函数：

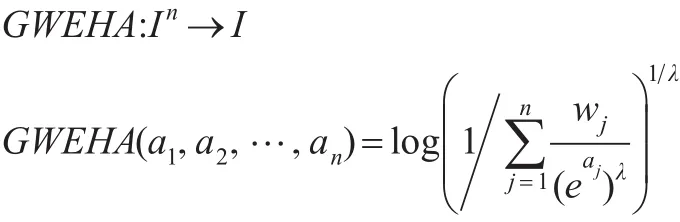
则称GWEHA为广义加权指数调和平均算子，简称GWEHA算子，其中 λ∈R-{0}，权重向量为 w=(w1，w2，…，wn)，且

若将GWEHA算子中的数据按降序排列，则可定义广义有序加权指数调和平均算子。

定义7：设 a1，a2，…，an∈I为待集成数据，若函数：

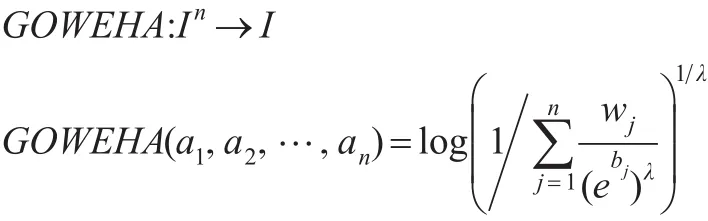
则称GOWEHA为广义有序加权指数调和平均算子，简称GOWEHA算子，其中λ∈R-{0}，bj是ai中第 j大的数，权重向量为

2.2 GOWEHA算子的性质

定理1：设 a1，a2，…，an与 c1，c2，…，cn为待集成数据，则：

（1）幂等性：若 ai=a(i=1，2，…，n)，则 GOWEHA(a1，a2，…，an)=a 。

（2）单调性：若 ai≤ci(i=1，2，…，n)，则 GOWEHA(a1，a2，…，an)≤GOWEHA(c1，c2，…，cn)。

（3）有界性：min{a1，a2，…，an}≤GOWEHA(a1，a2，…，an)≤max{a1，a2，…，an}。

（4）置换不变性：若 ci(i=1，2，…，n)是 ai(i=1，2，…，n) 的 任 意 一 个 置 换 ，则 GOWEHA(c1，c2，…，cn)=GOWEHA(a1，a2，…，an)。

证明：（1）若 ai=a(i=1，2，…，n)，则：

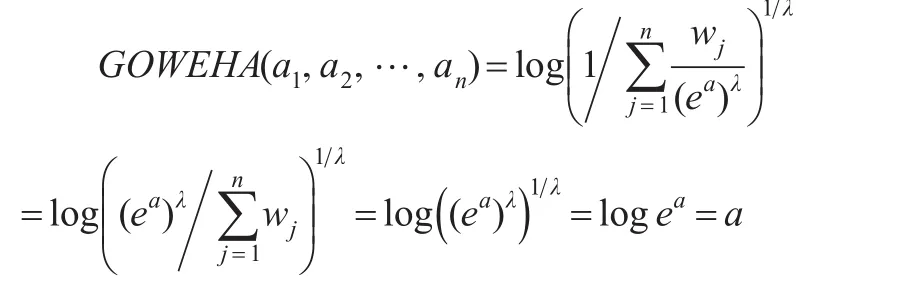
（3）由单调性和幂等性，易证。

（4）显然。

下面证明GOWEHA算子关于参数λ单调递减。

定理2：若 λ1≥λ2，则GOWEHA(λ1)≤GOWEHA(λ2)。

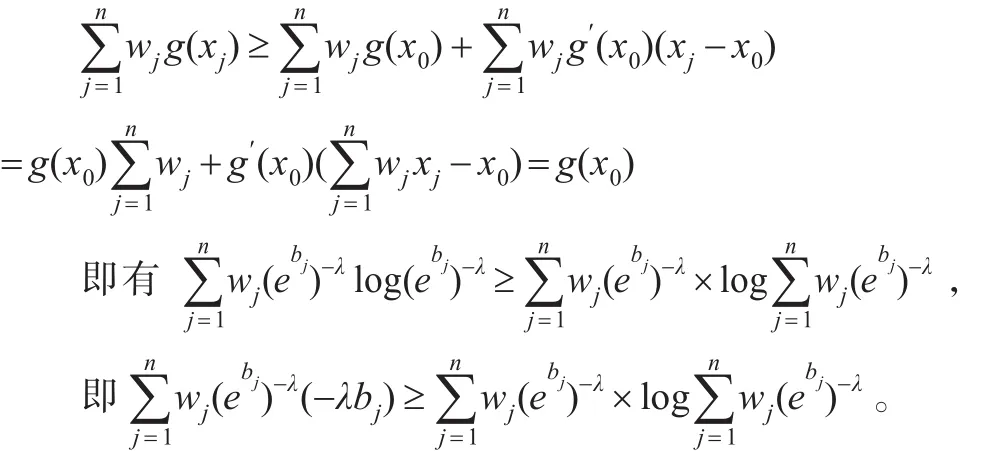
于是：

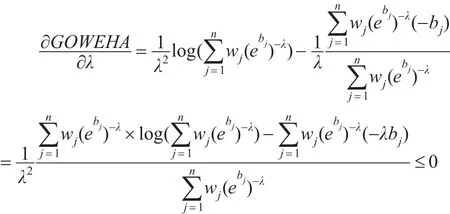
即GOWEHA算子关于参数λ单调递减。

2.3 GOWEHA算子的orness测度

定义8：GOWEHA算子的orness测度定义为：

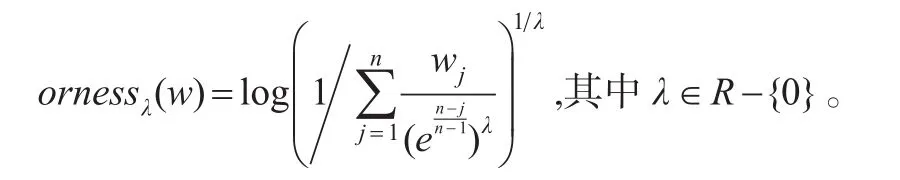
显然，w=(1，0，…，0) 时，ornessλ(w)=1 ；w=(0，0，…，1)时，ornessλ(w)=0。

由GOWEHA算子的幂等性和单调性，可得

定理3：0≤ornessλ(w)≤1。

定理4：若 λ1≥λ2，则 ornessλ1(w)≤ornessλ2(w)。

2.4 GOWEHA算子权重向量确定

当不考虑权重分布情况下，如果要求权重分量越接近越好，则可以在给定的orness水平下，通过构造下面优化模型来确定GOWEHA算子的权重向量：

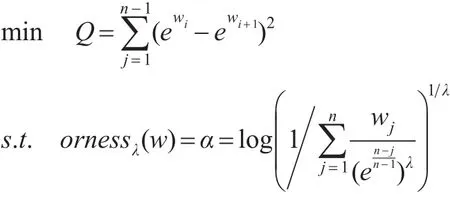
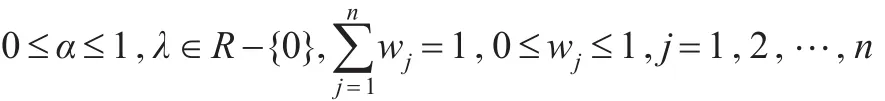
利用该优化模型求解GOWEHA算子权重向量的方法称为最小指数平方法。

例1：设 n=6，λ=1，orness水平分别为：0，0.1，0.2，…，0.9，1时，利用LINGO软件求得GOWEHA算子的权重向量见表1所示。

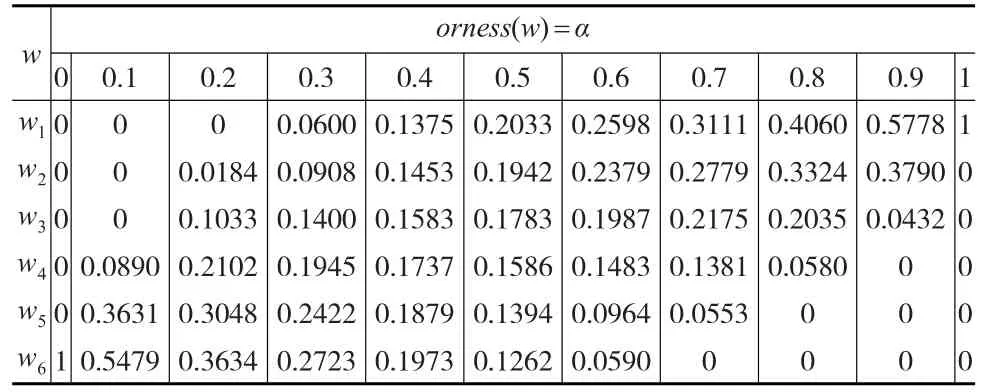
表1 GOWEHA算子的权重向量

由表1可以看出，随着orness水平增加，权重w1单调增加，而 w6单调递减，权重 w2，w3，w4，w5均为先增加后递减，且orness水平为0.5左右时权重相等。

3 决策应用

设 X={x1，x2，…，xm} 为方案集，C={c1，c2，…，cn} 为属性集。假设决策者给出的原始决策矩阵为A=(aij)mn，其中 aij(i=1，2，…，m，j=1，2，…，n)表示决策者给出的方案 xi关于属性 cj的属性值,w=(w1，w2，…，wn)为属性权重向量，且

为了可以直接集成属性值，需要对属性值进行规范化。属性可以分为效益型属性和成本型属性，令I1表示效益型属性，I2表示成本型属性，则由决策矩阵A可以得到规范化决策矩阵R=(rij)mn，其中

下面提出一种基于GOWEHA算子的多属性决策方法，具体步骤如下：

步骤1：专家根据实际情况创建原始决策矩阵A；

步骤2：通过规范化处理，得到规范化决策矩阵R；

步骤3：根据最小指数平方法，求出属性权重向量w=(w1，w2，…，wn)。

步骤4：利用GOWEHA算子，由规范化决策矩阵求出方案xi的综合属性值ri。

步骤5：根据方案xi的综合属性值ri的大小实现方案排序择优。

例2：某投资商准备投资一个公司，经过市场分析，他考虑了5家公司：x1为一家计算机公司，x2为一家汽车公司，x3为一家家具公司，x4为一家食品公司，x5为一家化工公司。为了选出最好的投资对象，该投资商组织了一个专家组对5家公司进行考察.经过仔细分析研究，专家组从6个方面对投资对象进行评价：c1为期望效益，c2为技术能力，c3为市场竞争力，c4为承担风险能力，c5为管理能力，c6为组织文化。专家给出的原始决策矩阵分别为：

根据专家组的原始决策矩阵，利用GOWEHA算子对5家待投资公司进行排序择优。

步骤1：专家根据实际情况给出原始决策矩阵,见表2所示。

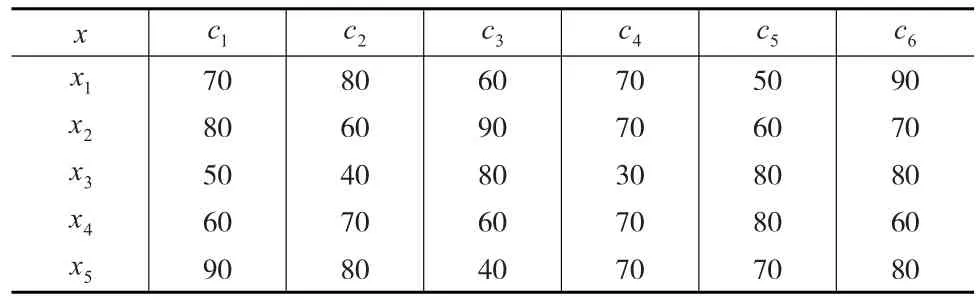
表2 原始决策矩阵A

步骤2：将原始决策矩阵规范化，得到规范化决策矩阵，见表3所示。

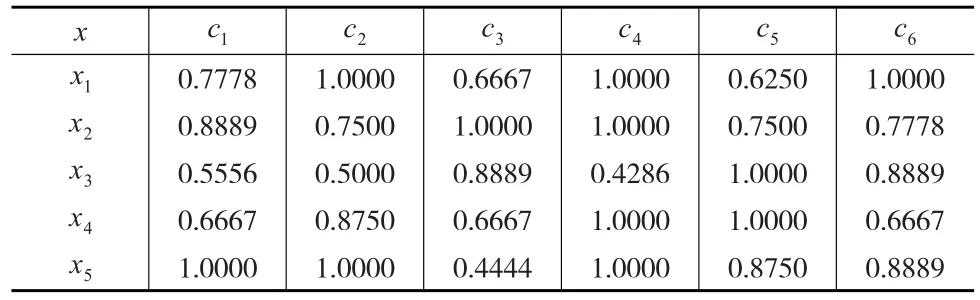
表3 规范化决策矩阵R

步骤3：根据最小指数平方法(λ=1，α=0.5，n=6)，求出 属 性 权 重 向 量 w=(0.2033，0.1942，0.1783，0.1586，0.1394，0.1262)。

步骤4：利用GOWEHA算子(λ=2)，求出方案 xi的综合属性值ri分别为：r1=0.8456，r2=0.8667，r3=0.6982，r4=0.8133，r5=0.8551

步骤5：根据r2>r5>r1>r4>r3可知，方案排序为 x2≻x5≻x1≻x4≻x3。因此，该投资商可以优先考虑向食品公司x2投资。

为了考查GOWEHA算子中参数λ对集成结果的影响，分别选取参数 λ=±1，±2，±5，±8，±10，计算出方案综合属性值，并将综合属性值和排序结果，见表4。同时将根据OWA算子,OWG算子和OWH算子得到的综合属性值和排序也一起列入表4。

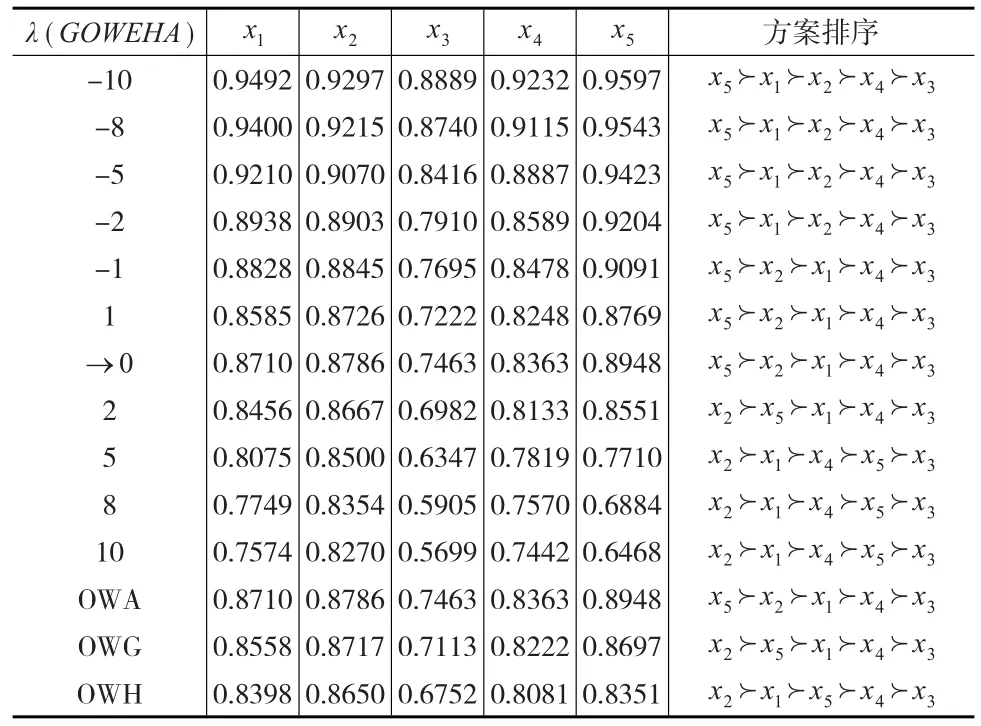
表4 方案综合属性值和方案排序

由表4可知，当 λ=-10，-8，-5，-2，-1，→0，1时，虽然方案排序略有变化，但是最优方案均为x5；而当λ=2，5，8，10时，方案排序稍微有变化，但最优方案为 x2；因此参数λ的变化会对方案排序结果有着重要的影响。由于λ→0时，GOWEHA算子的极限就是OWA算子，因此由二者得到的综合属性值和方案排序完全相同。同时，由OWG算子得到的排序结果与GOWEHA算子参数λ=2时方案排序完全相同。而由OWH算子得到的排序结果与GOWEHA算子参数λ=5，8，10时方案排序基本保持一致。因此从该例可以看出，通过OWA算子、OWG算子和OWH算子得到的方案排序可以归结为，当参数λ取不同值时，由GOWEHA算子得到的方案排序，故而GOWEHA算子更具有一般性。

4 结束语

根据罚函数思想，通过构建偏差函数定义了GOWEHA算子，并研究了其单调性、幂等性、有界性和置换不变性等性质。随后，定义了GOWEHA算子的orness测度，探讨了其orness测度的性质，并在给定orness水平下，提出了求解GOWEHA算子权重向量的最小指数平方法。最后，结合GOWEHA算子提出一种多属性群决策方法，并通过应用实例说明决策方法的可行性。研究结果进一步丰富了广义集成算子决策理论和方法。

[1]Harasnyi J C.Cardinal Welfare,Individualistic Ethics,and Interperson⁃al Comparisons of Utility[J].Journal of Political Economy,1955,(63).

[2]Aczel J,Alsina C.Synthesizing Judgement:A Functional Equation Approach[J].Mathematical Modelling,1987,(9).

[3]Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decision Making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,1(18).

[4]Herrera F,Herrera V E,Chiclana F.Multiperson Decision-Making Based on Multiplicative Preference Relations[J].European Journal of Operational Research,2001,(129).

[5]陈华友,刘春林,盛昭瀚.IOWHA算子及其在组合预测中的应用[J].中国管理科学,2004,12(5).

[6]Yager R R.Generalized OWA Aggregation Operators[J].Fuzzy Opti⁃mization and Decision Making,2004,(3).

[7]Bonferroni C.Sulle Medie Multiple Di Potenze[J].Bolletino Matemati⁃ca Italiana,1950,5(3).

[8]Beliakov G,Pradera A,Calvo T.Aggregation Functions:A Guide for Practitioners[M].Berlin:Springer,2007.

[9]Yager R R,Rybalov A.Understanding the Median as a Fusion Opera⁃tor[J].International Journal of General Systems,1997,(26).

[10]Calvo T,Mesiar R,Yager R R.Quantitative Weights and Aggregation[J].IEEE Transactions on Fuzzy Systems,2004,(12).

[11]Calvo T,Beliakov G.Aggregation Functions Based on Penalities[J].Fuzzy Sets and Systems,2010,(161).

[12]Zhou L G,Chen H Y.Generalized Ordered Weighted Logarithm Ag⁃gregation Operators and Their Applications to Group Decision Mak⁃ing[J].International Journal of Intelligent Systems,2010,(25).

[13]Zhou L G,Chen H Y,Liu J P.Generalized Weighted Exponential Proportional Aggregation Operators and Their Applications to Group Decision Making[J].Applied Mathematical Modelling,2012,(36).

[14]Zhou L G,Chen H Y,Liu J P.Generalized Logarithmic Proportional Averaging Operators and Their Applications to Group Decision Mak⁃ing[J].Knowledge-Based Systems,2012,(26).

[15]Zhou L G,Chen H Y,Liu J P.Generalized Multiple Averaging Oper⁃ators and Their Applications to Group Decision Making[J].Group Decision and Negotiation,2013,(22).

[16]Zhou L G,Chen H Y.Generalized Ordered Weighted Proportional Averaging Operator and Its Application to Group Decision Making[J].Informatica,2014,(25).

[17]Zhou L G,Tao Z F,Chen H Y,Liu J P.Generalized Ordered Weight⁃ed Logarithmic Harmonic Averaging Operators and Their Applica⁃tions to Group Decision Making[J].Soft Computing,2015,(19).