证据理论视角下区间概率信息风险型决策新方法
闫 英,周中林,袁 明,甘 蜜
(1.西南科技大学 经济管理学院,四川 绵阳 621010;2.西南交通大学 交通运输与物流学院,成都 610031)
0 引言
在现实的决策过程中,由于问题的复杂性、知识经验的限制和预测的不确定性,方案的属性或决策者偏好有可能表现为随机变量,即决策者无法准确预知未来的状态,但可以预估各种可能状态的概率,这类决策问题被称为风险型决策问题。由于风险型决策广泛存在于项目投资分析、风险评估、新产品研发评估等社会经济领域,因此近年来国内外学者开展了较多研究,其中区间概率信息条件下的风险型决策问题受到了较多关注[1-4]。
区间概率信息条件下风险型决策的关键是如何将区间概率合理转化为点概率,从而便于后续决策。文献[1]、文献[2]均采用C-OWA算子将区间概率转化为点概率,具有一定的合理性,但基本单位区间单调函数的确定具有较大的主观随意性,文中也未指出其确定的原则,因此有可能影响到决策的准确性;文献[3]从信息熵的角度出发,提出了一种基于最大熵准则的区间概率估计方法,通过求解最优规划问题可以将区间概率转化为点概率,但该方法存在区间概率改变时最优解可能不变的问题,可能得出有悖于常理的结论(详见实例分析);文献[4]提出了一种基于Monte Carlo模拟法的区间概率转化方法,该方法在其均匀分布假设下抽样求得的点概率实际上逼近于区间概率的中值,且不能保证转化后的点概率之和等于1。
实际上,从证据理论的角度来看,区间概率的下界即为信任测度,它表示对某状态发生为“真”的信任程度,是一种偏保守的估计;区间概率的上界即为似真测度,它表示对某状态不为“假”的信任程度,是一种偏激进的估计;它们与概率真值之间存在某种联系。基于此,本文拟从证据理论的视角出发,考虑所有状态发生可能性的信任测度和似真测度,从已知信息中推测概率真值的最可能估计值,从而较为客观的将区间概率条件下的风险型决策问题转化为点概率下的风险型决策问题。
1 证据理论简介
定义1[5]:设 Θ为辨识框架(The Frame of Discernment),m:2Θ→[0,1]是从幂集到区间数[0,1]的一个映射,即基本概率分配(Basic Probability Assignment,BPA),∀X,Y⊆Θ ,称由定义的函数Bel:2Θ→[0,1]为 Θ 上的信任函数(Belief Function);而由 Pl()X=定义的函数Pl:2Θ→[0,1]为Θ上的似真函数(Plausibility Function);X的信任区间为 P(X)=[Bel(X),Pl(X)]。
定义2[6]:设m是从幂集到区间数[0,1]的一个映射,即m:2Θ→[0,1],对于Θ的 n个子集 Ai(i=1,2,…,n) ,其区间基本概率分配(Interval Basic Probability Assignment,IBPA)为:

其中0≤ci≤di≤1。若IBPA同时满足以下条件:

则称m为有效的IBPA。
定义3[7]:若 m(Ai)=[ci,di]满足式(2),为有效的IBPA,当cj、dj同时满足以下条件时:

称m为归一化的IBPA。
若m为有效的IBPA但未归一化,则为了缩小区间宽度、降低信息冗余,需要按下式进行归一化处理:

2 证据理论视角下的区间概率信息转化方法
设需要在方案 ai(ai∈l,i=1,2,…,n)(l为决策空间)中做出决策,其中l有m个自然状态,第j个状态发生的概率为 Pj=[cj,dj](j=1,2,…,m),方案 ai在状态 j情况下的效用(或收益)为uij。根据EMV准则各方案的期望效用或收益为:

对于一组区间概率信息 Pj=[cj,dj](j=1,2,…,m),从概率论的角度来说有数学期望E(∑ )Pj=1;从决策者的角度来说希望Belj无限逼近Plj,这样区间概率就精确化为点概率,便于决策。然而,∑Belj≤1,因此1-∑Belj反映了已知区间概率信息对真实概率Pj低估的部分,称为下偏离度;∑Plj≤1,因此∑Plj-1反映了已知区间概率信息对真实概率Pj高估的部分,称为上偏离度。记:

则若α>β,即下偏离度大于上偏离度,说明相对似真函数,区间概率信息对信任函数的赋值过于保守,因此其点概率估计值应朝Plj的方向调整;反之,若α<β,则说明相对似真函数,区间概率信息对信任函数的赋值过于冒进,因此其点概率估计值应朝偏向Belj的方向调整。
基于以上思想,提出区间概率信息向点概率转化的公式如下:
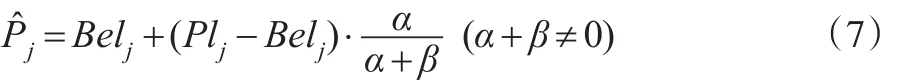
式(7)具有以下性质:

证明:

证明:当α=0时,有∑Belj=1,根据式(3)有 Belj≤Plj,同时根据式(2)有Belj≤Plj,两式联立求解有Belj=Plj。
当β=0时证明过程类似,在此不再赘述。
3 区间概率信息条件下的风险型决策
区间概率信息条件下的风险型决策步骤如下:
步骤1:根据式(2)检验区间概率信息是否为有效的IBPA。若无效,则需组织相关专家、进一步调研和评估后重新给出区间概率的预测值;
步骤2:若区间概率信息为有效的IBPA,则根据式(3)检验区间概率是否为归一化的IBPA,若不是,则按式(4)进行归一化处理;
步骤3:根据式(6)计算上、下偏离度α、β;
步骤4:根据式(7)将区间概率信息转化为点概率信息;
步骤5:根据EMV准则选出期望效用或收益最大的方案:

4 实例分析
例1:为便于比较,引用文献[3]中的例1进行分析。某厂决定生产一种新产品,有以下3个方案供决策:建立新车间大量生产(α1);改造原有车间达到中等产量(α2);利用原有车间设备小批试产()α3。市场对该产品的需求情况存在畅销、需求偏好、需求稍差和滞销4种自然状态,3种方案4种自然状态下的每月利润如下页表1所示。
根据市场调研、专家分析等综合研究,预测产品“畅销”的可能性为10%~25%,“需求偏好”的可能性为30%~60%,“需求稍差”的可能性为15%~35%,“滞销”的可能性为5%~15%。现需根据以上信息确定最优方案。
解:
步骤1:经检验,区间概率信息满足式(2),为有效的IBPA;
步骤2:根据式(3),验证区间概率信息为归一化的IBPA,因此无须再进行归一化处理;

表1 各方案每月利润表
步骤3:根据式(6)计算 α、β,结果为 α =0.4,β=0.55;
步骤4:根据式(7)将区间概率信息转化为点概率,结果如表2所示。表2中同时列出了本文方法和文献[1]、文献[3]法得到的点概率估计值。

表2 不同方法点概率估计值(例2)
步骤5:根据式(8)计算期望收益,结果如表3所示。表3还给出了文献[1]、文献[3]的计算结果,可见本文方法和文献[1]、文献[3]对决策方案的排序相同,即α1>α2>α3,最优方案为α1,表明了本文方法的正确性。

表3 不同方法EVM值计算结果(例1)
例2:若在例1中,通过分析预测产品“需求稍差”的可能性为15%~60%,其他已知条件不变,现需根据以上信息重新确定最优方案。
解:
步骤1:经检验,区间概率信息满足式(2),为有效的IBPA;
步骤2:经检验,区间概率[0.15,0.6]不满足式(3),因此需要按式(4)进行归一化处理,结果为[0.15,0.55];
步骤3:根据式(6)计算 α、β,结果为 α=0.4,β=0.35;
步骤4:根据式(7)将区间概率信息转化为点概率,结果如表4所示。表4中同时列出了本文方法和文献[1]、文献[3]、文献[4]方法得到的点概率估计值。

表4 不同方法点概率估计值(例2)
步骤5:根据EMV准则计算期望收益,结果如表5所示。表5还给出了采用文献[1]、文献[3]、文献[4]方法的计算结果。
从表5可见,本文方法和C-OWA算子法得出的结果极为相近,本文方法、C-OWA算子法、Monte Carlo法得出的决策方案排序均相同,即α1>α2>α3,最优方案为α2;而熵极大化法的排序结果却是α1>α2>α3,和其他3种方法得出的结论相矛盾。仔细对比表2与表4可发现,产品“需求稍差”的可能性由例1中的15%~35%变为例2中的15%~60%,从直观的分析来看,转化后的点概率应有所增加,本文方法和C-OWA算子法、Monte Carlo法获得的点概率估计值均和直观分析相符;而熵极大化法在例1、例2两种不同条件下得到的点概率估计值竟然完全相同,显然和客观信息不符,因此才会最终得到与其他方法相悖的排序结果。从熵极大化法建立的最优化问题来看,当区间概率发生改变时,最优化问题改变的仅仅是解得可行域,实际上,在一个较为宽泛的区间内,最优解是相同的,这就是区间概率信息改变而转化后的点概率不变的根本原因。虽然Monte Carlo法对决策方案的排序与本文方法相同,但从表4可知转化后的点概率不满足,因此对EMV值的评价是不准确的。

表5 不同方法EVM值计算结果(例2)
5 结束语
区间概率信息条件下的风险型决策是决策领域的一类特殊问题,本文从证据理论的视角,充分挖掘已知区间概率中隐含的信息,基于信任测度和似然测度提出了一种新方法。与已有几种方法的对比表明,新方法简单明了,具有较好的概率统计性质,且解释性较好,为区间概率信息条件下的风险型决策问题提供一种新的解决途径,具有较强的实际应用价值。
[1]陈春芳,朱传喜.区间概率信息条件下的风险型决策方法[J].统计与决策,2009,(8).
[2]刘培德,张新,金芳.区间概率条件下属性值为不确定语言变量的风险型多属性决策研究[J].管理评论,2012,24(4).
[3]何大义.区间概率信息条件下的风险型决策问题的解法探讨[J].运筹于管理,2007,16(6).
[4]何大义,周荣喜.区间概率信息条件下的决策方法[J].系统管理学报,2010,19(2).
[5]Dempster A P.Upper and Lower Probabilities Induced by a Multi-Valued Mapping[J].Annals of Mathematical Statistics,1967,38(4).
[6]Denoeux T.Reasoning With Imprecise Belief Structures[J].Interna⁃tional Journal of Approximate Reasoning,1999,20(1).
[7]Wang Y M,Yang J B,Xu D L,et al.On the Combination and Normal⁃ization of Interval-Valued Belief Structures[J].Information Sciences,2007,177(5).

