国际大宗商品与我国股市的极端风险溢出效应研究
赵新泉,孟晓华
(中南财经政法大学统计与数学学院,武汉430073)
0 引言
进入21世纪以来,随着金融市场极端风险发生的频繁性,人们越来越意识到风险控制的重要性,同时一个市场的波动还会波及到另一个市场,从而引发金融危机的传染和扩散。因此,研究不同市场之间极端风险的溢出效应,对于预测和防范极端风险跨市场的传递至关重要。
目前,国内关于大宗商品与我国股市之间溢出效应研究的文章还比较少,特别是针对极端风险的溢出研究也仅限于同一市场。因此,本文从信息溢出的角度,采用Hong等(2009)提出的基于VaR模型的风险-Granger溢出方法对三种主要的大宗商品铜、黄金、原油与股市之间极端风险溢出的方向及强度进行检验,并做了全面的分析和讨论。
1 极端风险溢出检验
研究两个市场之间的极端风险溢出效应,首先要对极端风险进行精确的估计,本文首先采用基于ARMA-GARCH模型的VaR进行极端风险测度,然后在此基础上进行极端风险溢出效应检验。
1.1 极端风险的测度
为了将极端上涨和下跌的风险有效地区分开来研究,本文采用VaR来度量极端风险。
定义1:对于商品上涨的VaR为P(Yt>Vt(up)|It-1)=α,则收益率条件分布的右α分位数对应于商品市场上涨的VaR。
定义2:对于商品下跌的VaR为P(Yt<-Vt(down)|It-1)=α,则收益率条件分布的左α分位对应于-Vt(down),定义Vt(down)为商品市场下跌的VaR。
现有研究表明,金融资产的收益率具有左偏厚尾、序列自相关和波动集聚等特征。因此,为准确估计VaR,本文采用ARMA-GARCH模型对收益率数据进行估计:
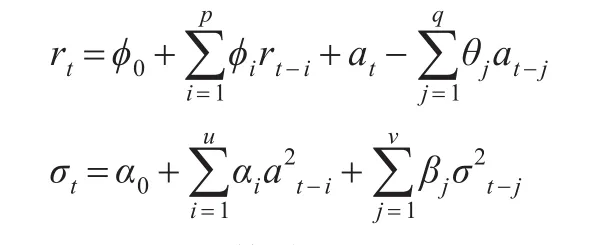
然后,根据估计的ARMA-GARCH模型得到收益率的条件期望和条件方差的一步向前预测:
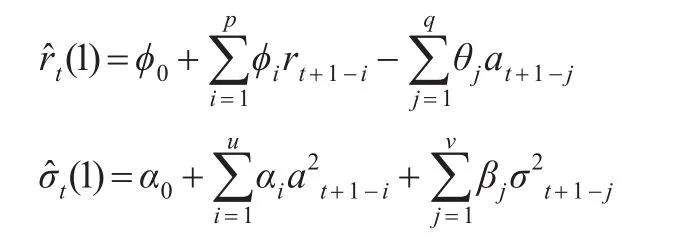
最后,再利用公式:
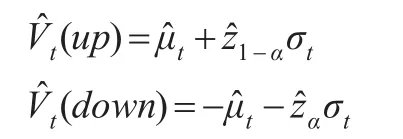
分别得到极端上涨和下跌风险的VaR。
1.2 VaR模型的检验
VaR估计的准确与否对后续的风险溢出检验至关重要,因此在进行极端风险溢出检验之前,需要先检验估计的VaR是否充分。本文采用Kupiec(1995)提出的Back-Testing方法进行检验,该方法把收益率超过估计的VaR值的例外情形看作一个二项分布中出现的独立事件。假定VaR的置信水平为1-α,样本容量为T,失效的天数为N,则失效的频率为f=N/T,失效率的期望值为α,然后用似然比率LR来检验零假设α=f是否成立。检验统计量为:
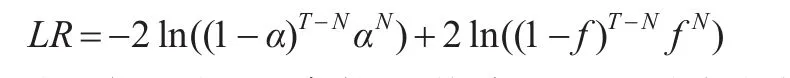
在原假设成立的条件下,统计量LR服从自由度为1的χ2分布。在95%的置信水平下,如果LR>3.84,则拒绝原假设,即估计的VaR模型是不充分的,否则认为是可接受的。
1.3 极端风险溢出检验
Granger因果关系检验主要有三种形式:均值-Granger因果检验、方差-Granger因果检验和风险-Granger因果检验。本文主要采用Hong等(2009)提出的基于VaR的风险-Granger因果检验方法进行极端风险溢出检验。
Hong等(2009)在总结前人研究的基础上,系统提出了信息溢出检验体系的Hong方法。该方法可以全面检验均值、波动率及极端风险VaR意义上的信息溢出,不仅能揭示信息溢出的方向和强度,而且检测效率也比传统的回归方法要高,是考察不同市场间信息溢出效应的一种行之有效的方法。
为检验两个市场之间的极端风险溢出效应,本文首先采用Hong基于VaR定义的风险指标函数。其中,极端上涨风险指标函数为:
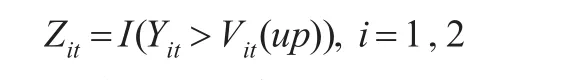
极端下跌风险指标函数为:
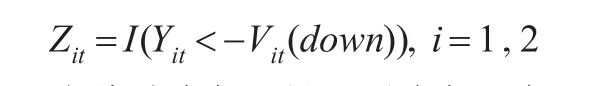
为检验市场2是否对市场1产生了单向的风险溢出,设定原假设时刻市场1和市场2的信息集,则之间的风险-Granger因果关系转化为风险指标序列Zit之间的均值-Granger因果关系,即只需要对Zit之间的交叉相关函数进行检验。
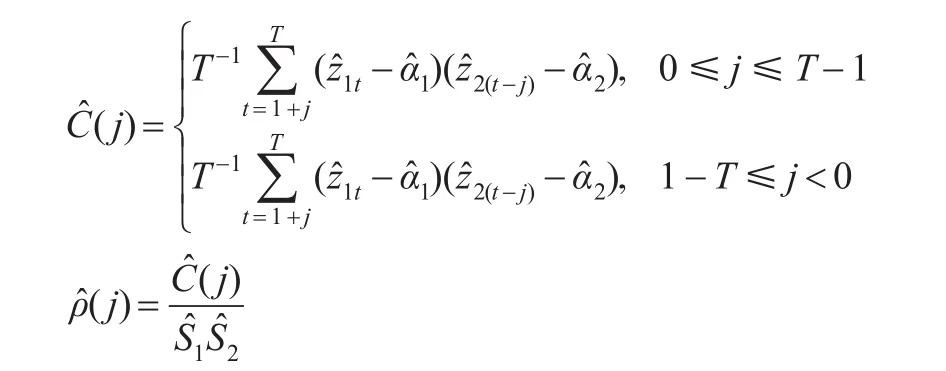
在H0成立的条件下,Q(M)收敛于标准正态分布。在检验中,可以通过比较Q(M)与标准正态分布右侧临界值来检验两市场之间是否存在极端风险溢出效应。
2 实证分析
2.1 数据的统计特征描述
关于大宗商品样本的选择,因为农产品的价格趋势主要与供给有关,与股市相关性较小,所以本文主要考查金属市场、能源市场与国内股市之间的极端风险溢出效应。沪深300指数样本覆盖了沪深市场六成左右的市值,具有良好的市场代表性,因此本文选择沪深300指数作为我国股市的代表。对于国际大宗商品市场,分别选择伦敦国际黄金现货定盘价、伦敦期铜综合指数、WTI原油指数作为国际黄金、铜和石油价格的代表。所有数据的时间段定为2007年1月4日至2016年8月10日,考虑到各国市场节假日等因素,在剔除了交易日不重合的数据后,共匹配得到2228个交易日的数据。数据来源于Choice金融终端和美国能源信息署网站,本文计算结果在R3.1.1下实现。考虑到时差滞后的原因,为了更准确地对比分析,在检验国内市场对国际市场的溢出效应时,采用国内t+1日的数据与国际t日的数据对应。令序列第t日的价格为Pt,则第t日的对数百分收益率为Yt=100ln(Pt/Pt-1)。收益率基本统计特征如表1所示。
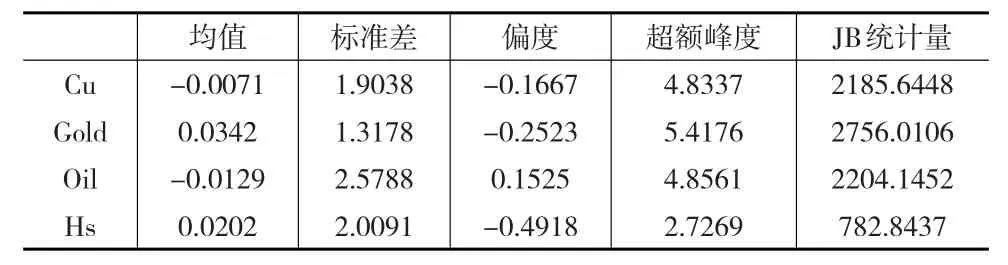
表1 收益率基本统计特征
由表1可以看出,2007年1月到2016年8月时间内所有收益率偏度均不为0,峰度均大于3,说明所有的收益率序列均呈现出明显的尖峰厚尾特点;同时J-B统计量都拒绝了正态分布,说明收益率分布是显著偏离正态分布的。
2.2 GARCH模型的建立
针对收益率尖峰厚尾有偏的特点,对于收益率的残差序列εt,本文假设其服从标准有偏广义误差SGED分布,其密度函数为:
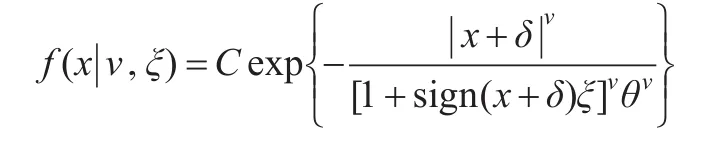
其中:
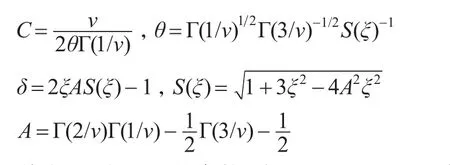
其中,v表示形状参数,当v<2时,相比正态分布具有更厚的尾部,当v>2时,相比正态分布具有更薄的尾部;ξ表示偏斜参数,当ξ<0时,表示分布尾部为左偏的,当ξ>0时,表示分布尾部为右偏的。特别地,当v=2,ξ=0时,SGED退化为正态分布。
对各个收益率序列建立ARMA-GARCH模型,结果见表2。
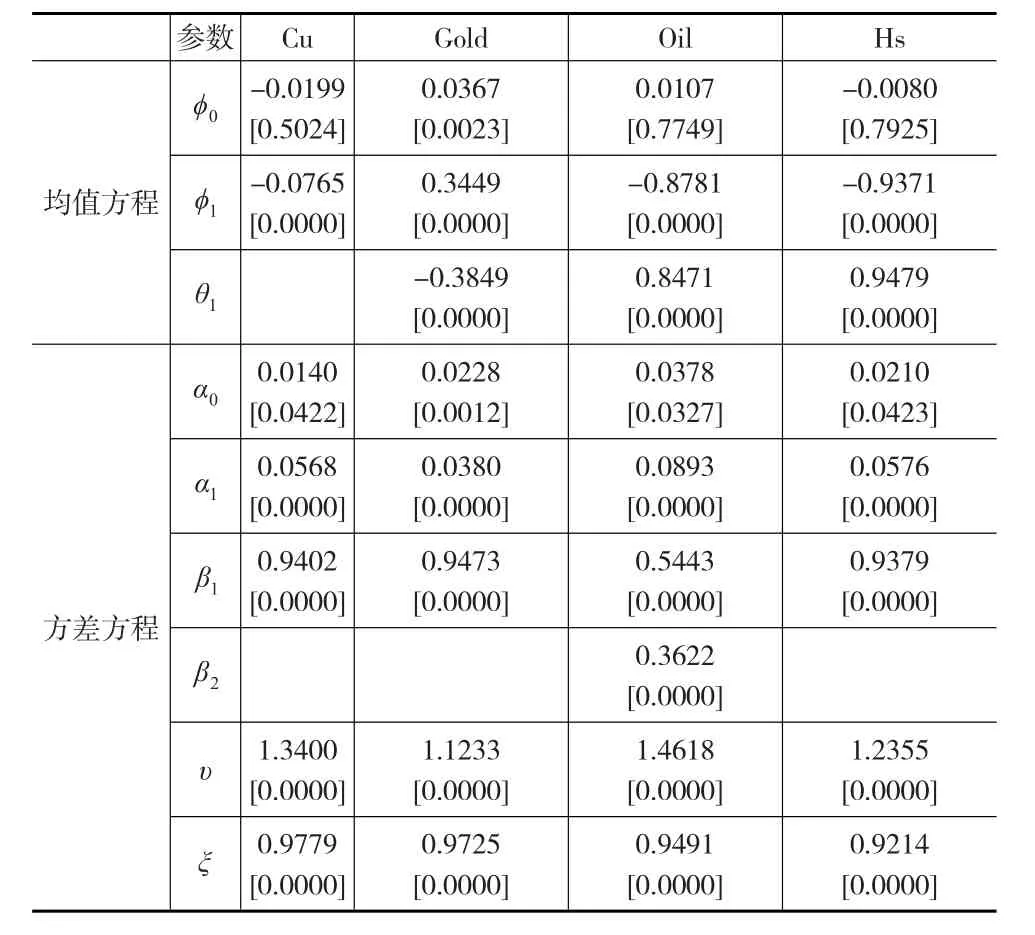
表2 收益率模型估计
根据表2的估计结果,在方差方程中,所有形状参数υ和偏斜参数ξ都是显著的,进一步说明收益率序列是有偏厚尾的。
2.3 VaR的估计和检验
根据估计的GARCH模型,计算出各个收益率序列的上涨和下跌的VaR值;对估计得到的所有VaR序列使用Kupiec提出的Back-Testing方法分别在95%和90%置信水平下进行检验,结果如表3所示。
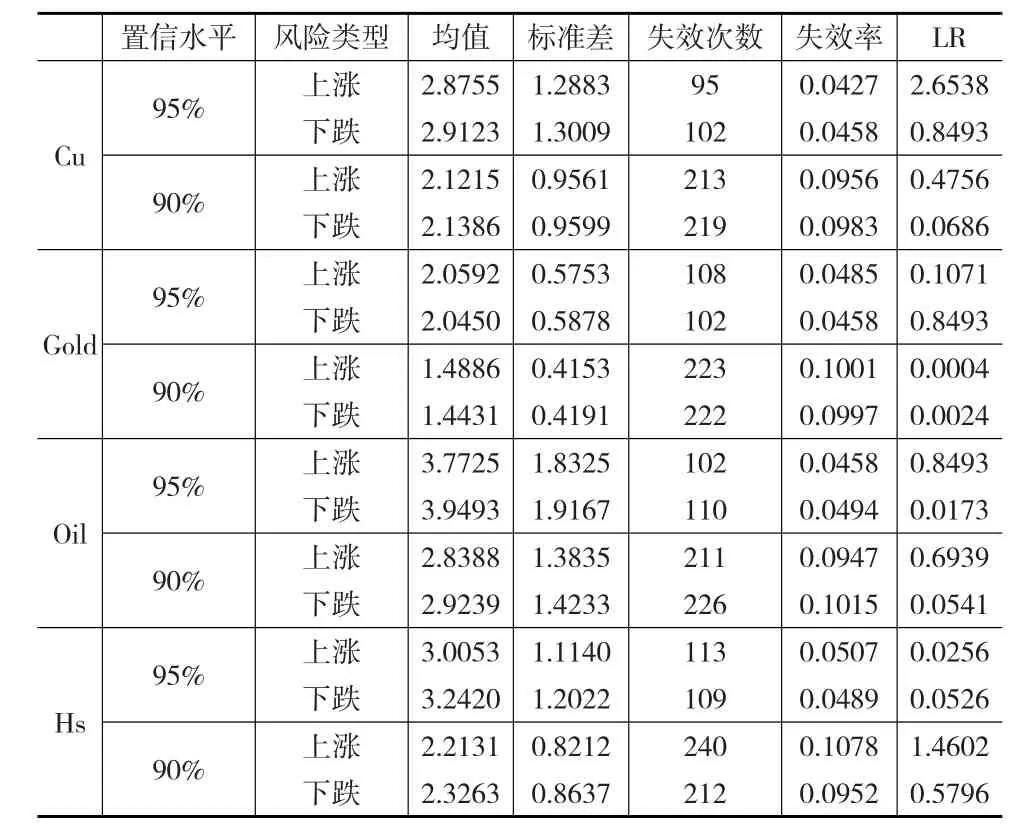
表3 VaR估计结果
由表3可知,所有收益率的LR统计量都小于3.84,由于LR统计量95%和90%置信水平下的临界值分别为3.84和2.71。说明估计得到的VaR模型在95%和90%置信水平下是充分的。同时,对于VaR的平均值,在同一置信水平下,极端上涨和极端下跌对于不同的市场主体造成的风险是不对称的。其中,铜、石油、股市在样本区间内下跌风险略大于上涨风险,说明极端下跌造成的风险损失更大,对多头来说更不利;黄金上涨风险比下跌风险造成的平均损失略大,说明极端上涨带来的风险损失更大,对空头来说更不利,应加大对上涨风险的防范。
接下来,分别在5%上涨风险和5%下跌风险下,运用Hong等(2009)提出的统计量对两个市场之间同方向的极端风险进行检验,其中M为有效滞后截尾阶数,依次取5、10、20,具体检验结果如表4和表5所示,表中数据为单向溢出检验统计量Q的值。
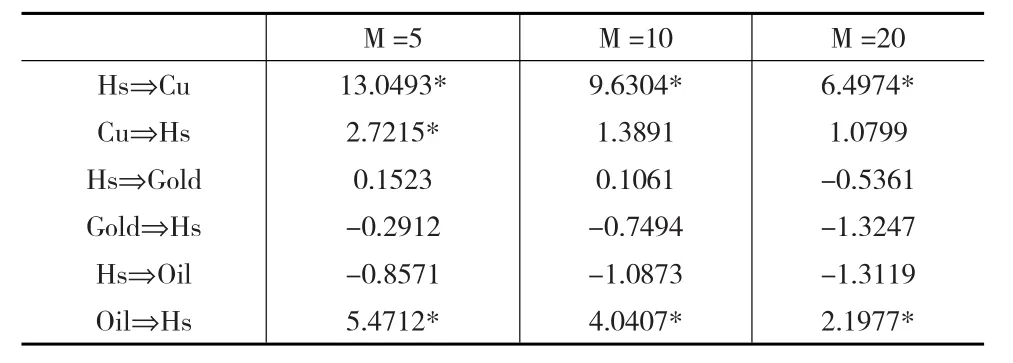
表4 上涨风险溢出
由表4和表5可以看出,在95%的置信水平下,伦敦期铜市场与沪深300指数之间具有显著的上涨和下跌风险溢出效应(不论参数M取值如何,只要有一个M值下Q是显著的即可认为信息溢出已经发生),且两者之间的溢出效应随滞后阶数的增加依次递减,说明两者之间的溢出效应不具有记忆性。同时,残差收益率的交叉相关系数只有一阶是显著的,说明信息传递的速度是比较快的。一般而言,信息大多从信息效率高的市场流向信息效率低的市场,说明伦敦期铜市场与沪深300指数之间信息交换效率比较高,当一个市场发生极端风险时,信息将很快传递到另一个市场。
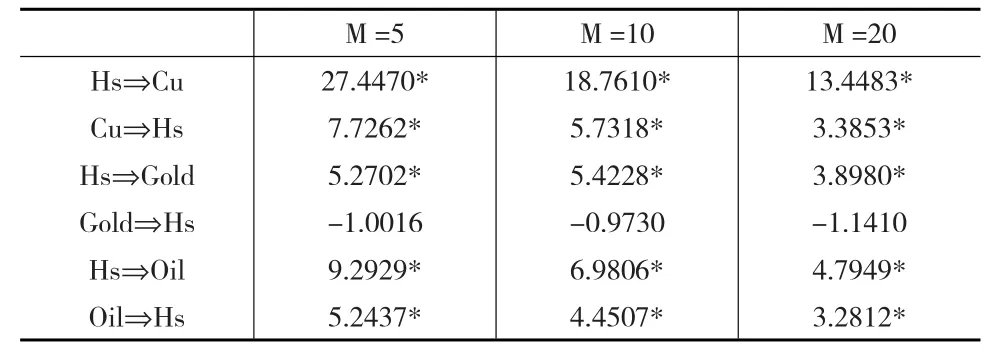
表5 下跌风险溢出
在95%的置信水平下,WTI原油和沪深300指数之间具有显著的下跌风险溢出,说明双方任一市场的下跌都将对另一市场的下跌具有风险溢出效应。同时,溢出效应具有不对称性,沪深股市对石油市场的溢出效应更显著一些。但上涨风险溢出只有单向的,即只有石油的上涨对沪深的上涨具有显著的溢出效应,反向的信息溢出不显著,说明在二者间的信息溢出中石油占绝对优势。沪深股市对石油价格的上涨更敏感一些,而沪深股市的上涨对国际石油市场影响不大。
在黄金和沪深股市的溢出关系中,只有沪深指数的下跌对黄金的下跌具有显著的溢出效应,其他均不显著。对于黄金和股市的联动关系,一般认为两者之间可能存在一定的负相关关系,因为黄金被看作是回避投资风险的避风港,在其他资产价值下跌的情况下,人们会青睐黄金。因此,黄金和股市之间可能存在反方向的极端风险溢出,即一方的上涨(或下跌)将对另一市场的下跌(或上涨)具有溢出效应。因此,接下来分别对黄金上涨和股市下跌、黄金下跌和股市上涨之间的极端风险溢出效应进行检验,结果如表6和表7所示。

表6 黄金上涨和股市下跌之间的溢出检验
由表6和表7可以看出,黄金和股市之间反方向的极端风险溢出效应不是很显著,只有黄金的上涨对股市下跌具有显著的溢出效应。而我国股市对国际黄金没有显著的反向溢出效应,说明国际金价受国内市场影响较小,我国金融市场的风险对其定价影响有限。以上结果说明,黄金与股市之间没有确定的风险传递关系,这与黄金价格的上涨和下跌受到政策等多方面因素的影响有关。对于股市投资者来说,可以选择黄金作为规避风险的投资产品。

表7 黄金下跌和股市上涨之间的溢出检验
3 结束语
根据本文的研究结果,国际铜、石油市场和我国股市之间存在着显著的极端风险溢出效应,且我国股市对国际大宗商品的溢出更强一些,具有信息先导的作用。黄金市场和我国股市的极端风险溢出相对微弱,这说明黄金作为具有一定货币属性的特殊商品,能为投资者提供良好的多元化风险分散作用。
[1] Hong Y,Liu Y,Wang S.Granger Causality in Risk and Detection of Extreme Risk Spillover Between Financial Markets[J].Journal of Econometrics,2009,(150).
[2] 陆凤彬,李艺等.全球原油市场间信息溢出的实证研究——基于CCF方法与ECM模型[J].系统工程理论与实践,2008,(3).
[3] 洪永淼,李艺,陆凤彬等.国内外期货市场间信息溢出效应的实证研究——基于均值、方差和风险Granger因果关系[J].经济学报,2008,3(1).
[4] 潘慧峰,张金水.国内外石油市场的极端风险溢出检验[J].中国管理科学,2007,(6).
[5] 李红权,洪永淼,汪寿阳.我国A股市场与美股、港股的互动关系研究:基于信息溢出视角[J].经济研究,2011,(8).
[6] 周翔,蒋翔林.全球股指现货和期货市场极端风险溢出检验[J].统计与决策,2009,(17).
[7] 吴鑫育,马宗刚,汪寿阳,马超群.基于SV-SGED模型的动态VaR测度研究[J].中国管理科学,2013,21(6).

