中国人口的初婚年龄分布与差异分析

石国平，李汉东

（北京师范大学政府管理学院，北京100875）

0 引言

改革开放以来，中国社会和经济取得了的巨大发展，加之中国实施的计划生育政策，使得中国的初婚模式产生了深刻变化，并成为人口学研究的一个重要领域。但现有的对于中国初婚模式的研究，由于受到人口数据的局限，主要集中在平均初婚年龄及其趋势、夫妻年龄差等方面的分析。已有研究在对初婚模式的分析和测度方面的指标和分析方法也较为简单，无法综合考察初婚模式变动的趋势和不同人口群体之间的差异，特别是对我国城乡差异以及教育程度差异对初婚模式的影响的研究尚处于空白。本文首先基于观察数据建立了初婚年龄分布的一般模型，并提出了一种改进的估计初婚年龄分布的方法，然后进行了实证分析，给出了我国25年来初婚年龄分布的变化趋势，并比较了城镇乡人口群体的初婚年龄分布差异以及不同教育程度人口群体的初婚年龄分布差异情况。

1 研究方法

1.1 初婚模型

自从寇尔（1971）发现人口的初婚模式以来，围绕初婚模式的研究层出不穷。为改进对初婚年龄分布的估计效果，人们先后提出了许多的改进模型（Kostaki，2009）。但是由于实际人口数据存在一定的误差，特别是年龄别初婚率往往存在一定的进度效应和随机干扰现象，所以直接对数据进行拟合并不一定能得到真实的初婚年龄分布。为此，本文提出一个一般的初婚年龄分布模型。

设Y为某一特定人口中观察到的初婚年龄，且满足：

其中X是取非负值的随机变量（可理解为人口的内在初婚年龄），ε是随机项，且满足ε～N(μ0，,即若μ0≠0，则存在一个与内在初婚年龄不同的平均进度或扰动效应。这里我们假设X和ε相互独立。

显然，Y的分布由X和ε的分布共同决定。在给定X的分布的条件下，Y的分布可通过相互独立的连续随机变量和的卷积公式来求出。其一般表达式为：

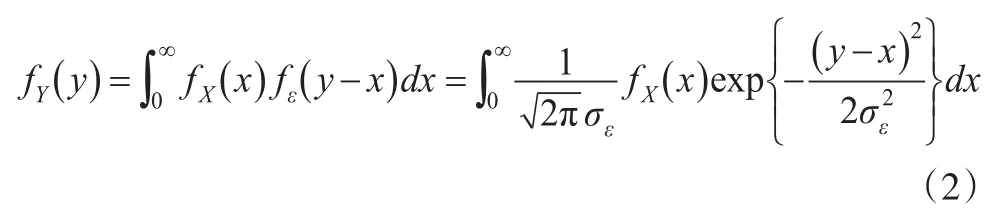
关于fX(x)的形式，前面已经介绍了多种模型，最近的一个模型是由Peristera和Kostak（i2007）提出的，简称之为P-K模型。该模型如下：

其中x代表育龄妇女初婚年龄，c1，μ为参数。当x≤μ，σ（x）=σ11；当x≥μ，σ（x）=σ12。c1描述的是基准初婚水平，它和初婚率有关。μ反应了分布的位置，σ12分别反应了初婚率在峰值前后的分布。

在模型（3）的基础上，Peristera和Kostaki（2007）提出了可供选择的另一个模型，该模型可以很好地描述存在两次初婚高峰的情形，称为P-K扩展模型，该模型如下：

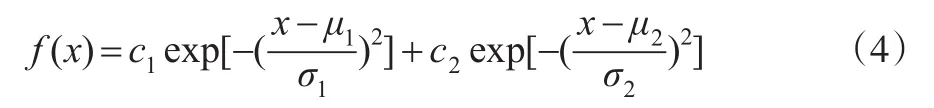
其中参数μ1、μ2反映了两次初婚高峰的平均年龄，σ1、σ2反映了两次初婚高峰的方差，c1、c2反映了两次初婚高峰剧烈程度。

在给定fX(x)的形式下，通过计算可以给出一些一般的结论。

引理2：若X服从P-K扩展模型，即：

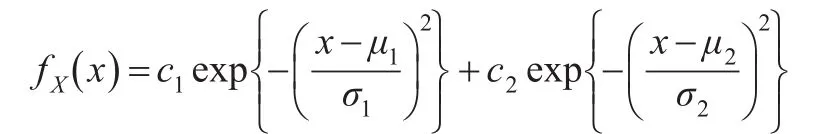
则有：

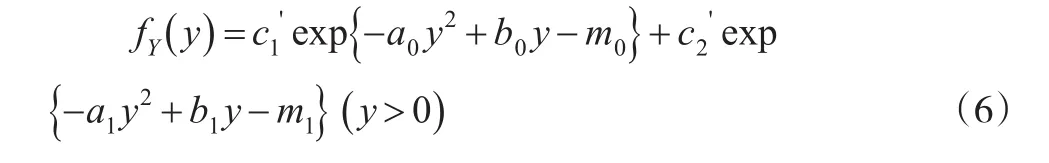
其中：

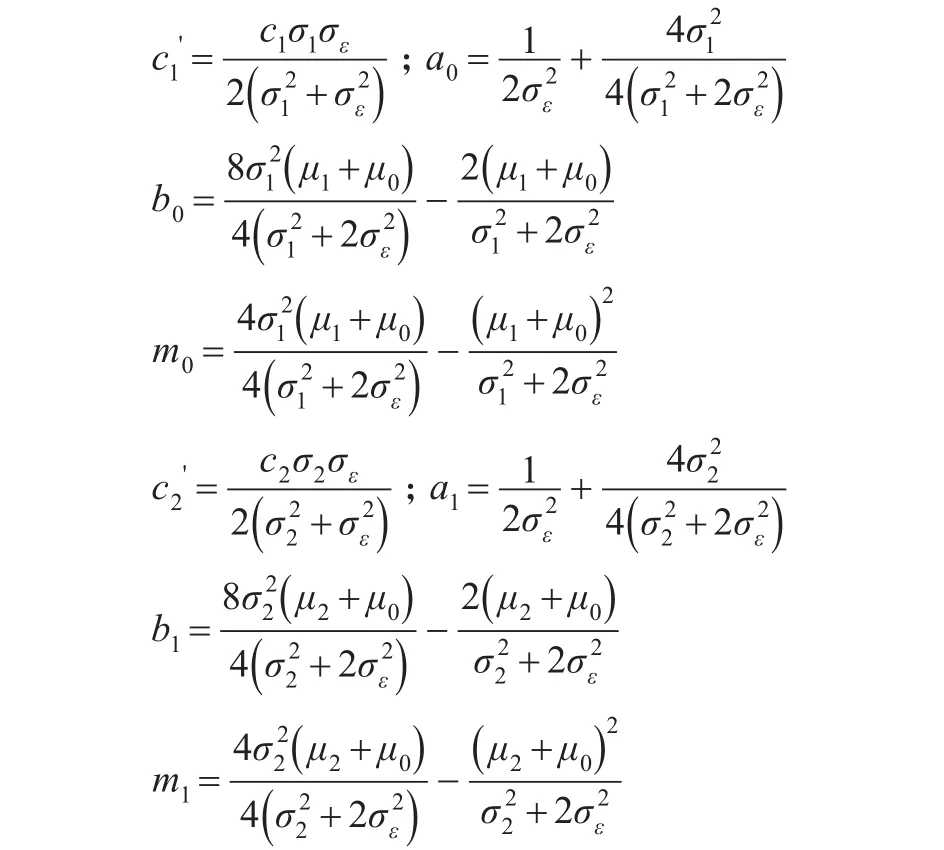
从上述结果看，如果初婚年龄分布受到随机因素的干扰，将使得观察到的初婚年龄分布非常复杂。但由于观察到的初婚年龄是相互独立的内在初婚年龄和随机扰动项的和，所以可以得到最重要的数字特征，如期望和方差：

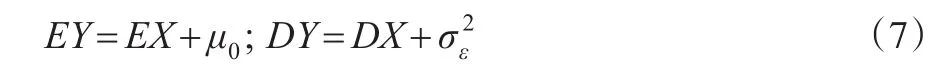
这一关系是简洁的，其中称EY为样本均值，EX为拟合均值，DY为样本方差，DX为拟合方差。因此，在实际中，本文可采用两步法，即首先对数据进行拟合，并将拟合数据与实际观察数据分别计算各自的均值和方差；然后将得到的均值和方差分别进行比较，以判断拟合模型的拟合效果。

1.2 年龄别初婚率的计算

本文所使用的与年龄别初婚率有关的数据来自中国历年的人口统计数据。由于部分普查数据如“六普”数据中仅提供了分年龄的婚姻状况人口数据，没有直接给出年龄别初婚率（更不用说同一队列人口的年龄别初婚率）。因此，本文需要将分年龄的不同婚姻状况的人口数据进行处理，以得到近似的同一队列人口的年龄别初婚率。为此，本文提出了以下方法：

首先，对于某一特定年龄，普查数据给出了该年龄段人口的总数和分婚姻状况的人口数。在该年龄段所有已婚人口中由于包含了再婚的人口比率，因此需要将再婚的人口数量从该年龄队列的人口数量中去掉，剩下的就是该年龄的初婚人口累积人数，除以该年龄总人口数就可得到该年龄的累积初婚率。其次，由于该年龄段的累积初婚率是由该年龄及以前的各年龄的初婚率累加而成的（如在20岁人口中，一个人处在初婚状态，则他或她可能是在20岁完成的初婚，也可能是在19岁或18岁完成的初婚），因此将该年龄之前的各年龄初婚率去除就是该年龄的初婚率，然后将结果归一化就得到分年龄的初婚率。最后，借鉴总和生育率的计算方式，将同一时点不同队列的分年龄人口看作是同一队列经历不同年龄的人口,就得到同一队列人口的近似年龄别初婚率。在此基础上，通过本文给出的一般方法就可以得到某一队列人口的初婚年龄分布。

上述步骤可用数学公式表示如下：

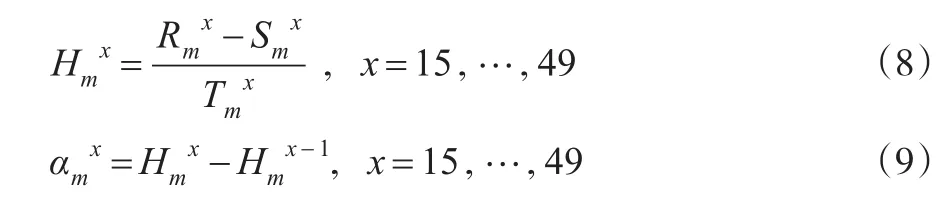
显然有：

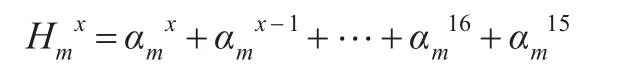
此外需要说明，由于实际数据取自不同年龄队列，每一年龄队列的总人数并不相同，而且可能会存在低年龄队列累积初婚率高于高年龄别累积初婚率的情况，因此，在计算中需要保证高年龄队列的累积初婚率要高于低年龄队列人口的累积初婚率（如出现这种情况则需要通过对两相邻队列人口的累积初婚率进行线性插值计算），这样调整后得到的不同队列人口的年龄别初婚率可近似看作同一队列人口的年龄别初婚率。

2 实证分析

2.1 数据以及处理

本文选取的数据出自1985以来的历年人口统计数据，包括《中国1990年人口抽样调查资料》、《中国2000年人口抽样调查资料》、《中国2005年1%人口抽样调查资料》以及《中国2010年人口抽样调查资料》数据。录入的数据包括“全国男性总人口”、“全国男性初婚”、“全国男性已婚”、“全国女性总人口”、“全国女性初婚”、“全国女性已婚”以及分年龄别男女（15～49岁）人口数,总出生人口数,分城镇乡的初婚人数以及受教育程度的初婚人数。

对得到的同一队列的年龄别初婚率本文使用P-K扩展模型进行拟合。

2.2 中国初婚年龄分布随时间的变化趋势

为研究我国20世纪80年代以来初婚年龄分布的变化趋势，本文选择了1985年、1995年、2000年、2005年和2010年全国男性和女性人口数据，采用上述介绍的方法，得到了中国自1985—2010年的分性别初婚模式变化情况，结果如图1所示。

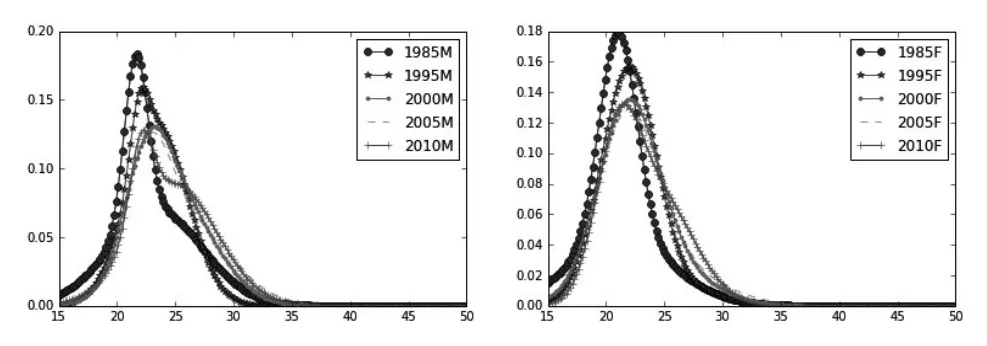
图1 1985年、1995年、2000年、2005年和2010年初婚年龄分布曲线

从图1中可以看出中国男性和女性人口从1985—2010年之间初婚的年龄分布存在一定的差异，且呈现出随时间增加分布的峰值下降和整体分布向后延迟的趋势。无论男性还是女性的初婚年龄分布，1985年和1995年呈现明显尖峰的形状，而2000年后则分布高峰的陡峭程度下降，而且2000年、2005年2010年这三年无论男性还是女性的分布存在明显的相似性。这一性质表明中国的初婚模式从80年代以来经历了一个明显的变化，而到2000年以后初婚模式相对变化较小。

从图1中可观察的另外一个变化是分布曲线随着时间增加存在明显的右拖尾现象，即无论男性还是女性随着时间推移，在高年龄段选择初婚的比例逐渐增加，与八、九十年代的初婚年龄相对集中存在比较明显的差异，这一变化可通过分布的数字特征表现出来。表1分别给出了样本均值、样本方差、拟合均值和拟合方差的计算结果。

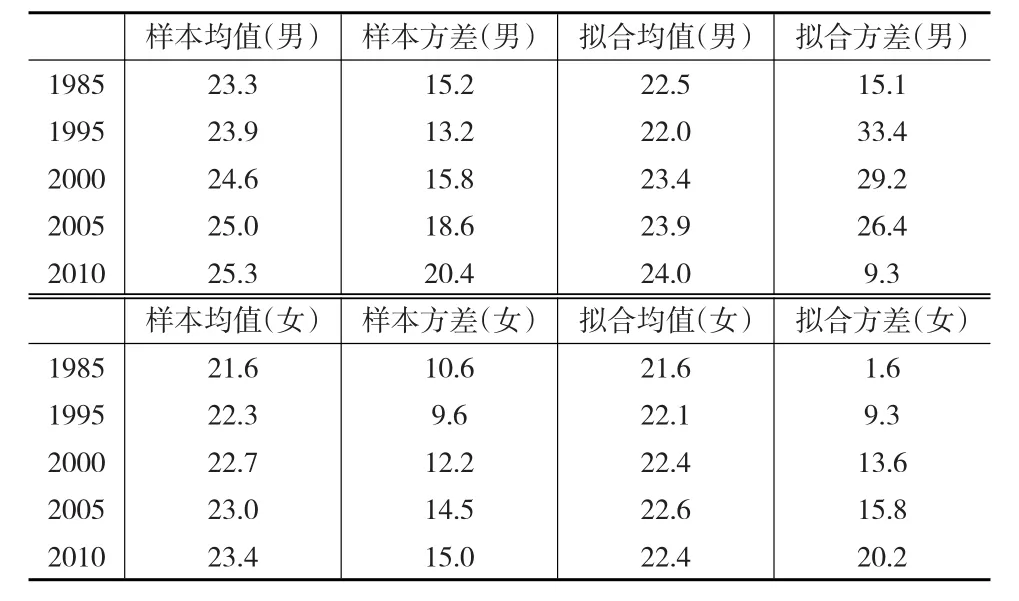
表1 历年样本的均值、样本标准差和拟合均值、拟合标准差

从表1中数据可以看出，我国25年来男性和女性初婚模式都发生了一定的变化，初婚年龄样本均值从1985—2010年有明显的提高，其中男性的样本均值从23.3岁提高到了25.3岁，25年提高了2岁，平均每年提高0.08岁，女性初婚年龄样本均值从21.6岁提升到23.4岁，25年来提高1.8岁，平均每年提高0.072岁。男性初婚平均年龄延迟程度略高于女性。对比实际数据和拟合分布的情况，可以看出男性的拟合均值小于样本均值，这也与图形中男性实际初婚年龄分布出现的剧烈变动有关，也表明男性的初婚年龄数据存在一定的干扰。而女性的拟合均值与样本均值有着高度的相似，拟合方差也小于男性，这表明模型对女性的初婚年龄描述上要好于男性，也可以认为女性的随机扰动相比男性而言更小，她们在初婚年龄上更加稳定。这里不难看出，尽管最近10几年中国初婚年龄分布的形状存在高度的相似，但中国平均初婚年龄在逐年上升，这与图像中所观察的拖尾的结果是相吻合的。

表1中反映出另外一个重要信息是男女平均婚龄差的变化。从历年样本均值来看，1985年男女平均初婚年龄差为1.7岁，而到2010年相差为1.9岁，所以整体来看男女初婚的平均年龄差变化不大，这是由于男性和女性的平均初婚年龄都增加了，且增加的幅度是相近的。

2.3 中国初婚年龄分布的城镇乡差异比较

为分析城镇乡因素对男女初婚年龄分布的影响，本文分别选择1990年和2010年的数据进行了统计分析。由于两组数据结果相近。本文以2010年为例给出分城镇乡的男女性人口的初婚年龄实际分布，如图2所示。

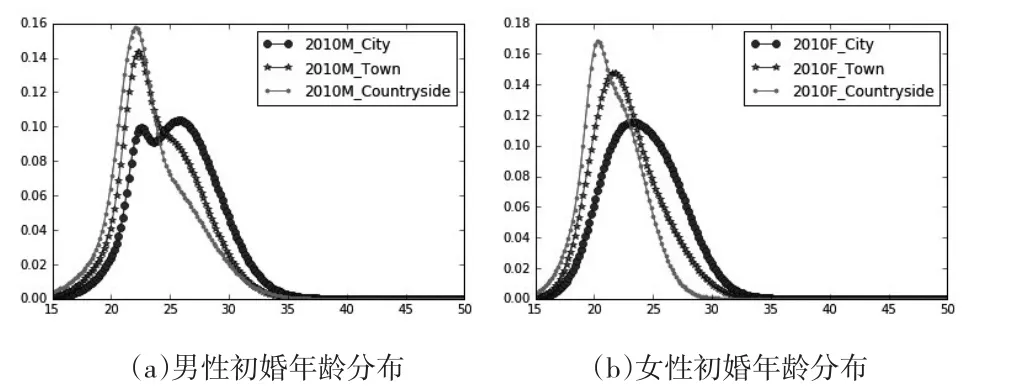
图2 2010年分城镇乡的初婚年龄样本曲线

图2（a）给出了城镇乡的男性初婚年龄分布曲线，可以看出乡村和镇的男性初婚年龄分布呈现明显的相似性，而城市男性的初婚年龄分布曲线呈现出了双峰的分布趋势，且与乡镇的分布呈现明显的差异，表现为更平的峰部和宽和后延的曲线形状。从图2（b）中可看出与男性初婚年龄分布相似的结果，但与男性初婚年龄分布曲线相比，城市女性的初婚年龄分布更平滑，且没有出现双峰分布的情形。

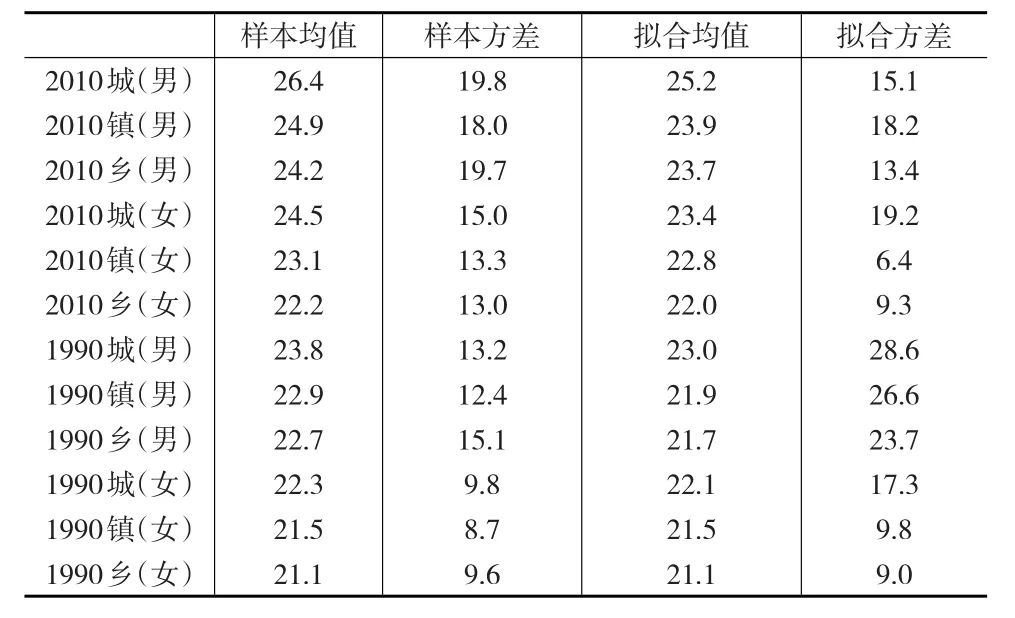
表2 1990年和2010年分城镇乡样本均值、样本方差和拟合均值、拟合方差

从表2中可以观察到，2010年样本均值与1990年样本均值相比，男性城市人口增加了2.6岁，男性城镇人口增加了2岁，男性乡村人口则增加了1.5岁；与此同时，女性城市人口增加2.2岁，女性城镇人口增加了1.6岁，女性乡村人口增加了1.1岁。这与前面分析的平均结婚年龄随时间增加的趋势是一致的，同时也表明无论男性和女性，随着时间的增长，存在着平均初婚年龄从城市到城镇再到乡村的递减效应。

而从同一时间点来看，无论男性还是女性，平均初婚年龄也同样存在着城镇乡的递减效应。如从样本均值看，2010年的男性城市人口比城镇人口平均初婚年龄多出1.5岁，比乡村人口多出2.2岁；女性城市人口比城镇人口平均初婚年龄多出1.4岁，比乡村人口多出2.3岁。与此同时，1990年的男性城市人口比城镇人口平均初婚年龄多出0.9岁，别乡村人口多出1.1岁；女性城市人口比城镇人口平均初婚年龄多出0.8岁，比乡村人口多出1.2岁。可见随着时间的推移，男女人口平均初婚年龄存在的城镇乡差异进一步增大。

而从男女平均初婚年龄差的角度来看，2010年城市人口为1.9岁，城镇人口为1.8，乡村人口为2岁；1990年城市人口为1.5岁，城镇人口为1.4岁，乡村人口为1.6岁。可以看出城镇乡的平均初婚年龄差相差不大，且随着时间增长，平均初婚年龄差有增加的趋势。

另外需要说明，拟合模型的平均初婚年龄和样本初婚年龄相差不大，方差亦稳定，说明本文的模型在描述分城镇乡的男女初婚年龄上效果良好。其中同一年的城市男性和女性的平均初婚年龄要高于乡村男性的平均初婚年龄的2岁左右，可以看到平均初婚年龄随着由乡到镇再到城市的依次后移的趋势，不难推出平均初婚年龄和区域的社会经济发展水平有着密切的联系。

2.4 教育程度对初婚模式的影响

为考察不同教育程度人口群体在婚姻选择上的差异，本文根据2010年男性和女性受教育程度的婚姻状况数据，来给出其初婚年龄分布。其中男女性的教育水平分为未上过学、小学、中学和大学四个程度。图3给出了根据实际数据绘制的初婚年龄分布曲线。

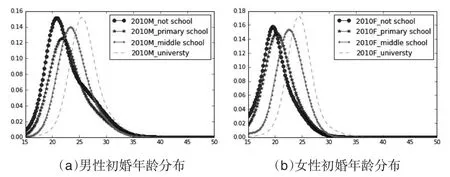
图3 2010年分教育水平的男女初婚年龄分布曲线

从图3中可以看出，无论男性还是女性，受教育水平越高，初婚年龄分布曲线越向右移，且初婚的平均年龄增大。为进一步说明初婚模式和初婚年龄的变化，本文分别计算了不同教育程度下的男女人口初婚年龄分布的样本均值和样本方差以及拟合均值和拟合方差，通过比较来判断生育模式随时间变化情况，如表3和表4所示。

表3 分教育程度男性样本均值和方差以及拟合均值和方差

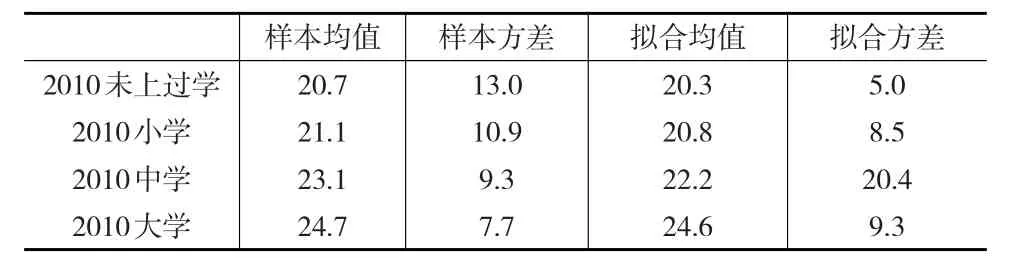
表4 分教育程度的女性样本均值和方差以及拟合均值和方差

根据表3和表4，可看出其有以下特点：

（1）随着受教育程度的升高，其初婚年龄的样本均值有明显的后移，其样本均值变化较大。对男性来说，大学教育程度人口比中学教育程度人口增加1.8岁，比小学教育程度人口增加2.7岁，比未上学人口增加2.8岁；对女性来说，大学教育程度人口比中学教育程度人口增加1.6岁，比小学教育程度人口增加3.6岁，比未上学人口增加4岁。女性人口平衡初婚年龄受教育程度的影响高于男性。

（2）与之前的不同年份的初婚年龄样本均值与拟合均值相比，在分教育程度的初婚年龄拟合均值上虽然都略小于样本均值，但大多数都在1岁的误差范围内，方差除了个别偏离程度较高，大部分都较低，模型整体对样本的描述是稳健的。

已有的研究将人口区分为接受高等教育和未接受高等教育两个群体，并研究高等教育与对人口婚姻选择行为的影响。上述分析也表明接受高等教育的人口群体其初婚平均年龄明显高于其他教育程度群体。因此，本文将教育进一步分为大学与未上过大学两个条件来讨论，并得到如下结果，见表5所示。

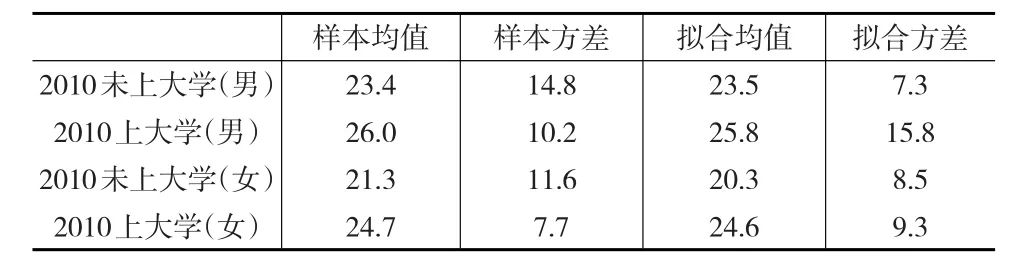
表5 分教育程度的男性与女性样本均值和方差以及拟合均值和方差

从表5可以看出在接受大学教育与不接受大学教育的男女群体中平均初婚年龄都相差较大，其中男性的差值在2～3岁之间，而女性差值更是达到了3～4岁，都大于全国平均初婚年龄差值，说明是否接受大学教育的男性和女性在初婚年龄选择上会产生明显的影响，相比而言这一因素对女性初婚年龄选择上产生的影响比男性更大。

3 结论

本文从男性和女性两个角度,对全国初婚年龄进行了探讨，在时间维度上进行了纵向比较；并选取了受教育程度与城镇化水平这两点，在空间维度上进行了横向比较，综上所述，20世纪80年代以来，中国的初婚年龄分布发生了明显的变化，并且中国的初婚年龄分布呈现出明显的城镇乡差异和教育程度的差异。具体的结论如下:

（1）中国20多年来的人口的平均初婚年龄稳定增长。虽然增长并不高，但总体增长趋势较为平稳。而且早婚现象仍然存在（如15岁，16岁左右），但这一年龄的初婚率却逐年下降，而25～30岁初婚率却在这25年来逐渐增高，这也与我国男女婚姻观念更加开放，对婚姻要求更高相符合。其中男女平均初婚年龄差在1985—2010年都有所增长，也体现我国现在男性生活工作压力越大，对初婚年龄的选择延迟会远高于女性。

（2）中国人口的初婚年龄分布存在明显的城镇乡差异。这种差异表现在三个方面：一方面是随着时间增加，无论男性还是女性其初婚模式都存在延后的趋势；二方面是无论男性和女性，都存在着平均初婚年龄从城市到城镇再到乡村的递减效应；三方面是城镇乡的男女平均初婚年龄差相差不大，但同样存在随时间增加的趋势。

（3）教育程度对中国人口初婚年龄分布存在明显影响。平均初婚年龄在受教育程度不同的情况下呈现男高女低的现象,但是随着受教育程度的升高，二者之间的差距会有所降低。接受高等教育的男女人口其初婚年龄分布没有显著差异，但存在明显的向右延迟现象。

以上分析都是建立在初婚模式模型和经验分布的基础上的。由于初婚模式相对不容易受到出生人口漏报的影响（当人口漏报是均匀分布的时候），因此，本文的分析结果有利于对初婚率的变化进行判断。当然，本文选择的拟合模型隐含了双峰分布的假设，在模型的拟合中可以看出来当初婚率变动剧烈时效果会更加好，也更加接近本文的模型描述。

[1] Hajnal J.European Marriage Patterns in Perspective[M].London:Ed⁃ward Arnold，1965．

[2] Ansley J C.Age Patterns of Marriage[J].Population Studies,1971,25(2).

[3] Peristera P,Kostaki A.Modeling Fertility in Modern Populations[J].Demographic Research,2007,16(6).

[4] 易翠枝.婚姻市场的教育分层与女性人力资本投资[J].华东经济管理，2007,(2).

[5] 陈正伟.中国初婚年龄性别匹配模型及应用[J].统计与决策，2010,(3).

[6] 韦艳，董硕，姜全保.中国初婚模式变迁——基于婚姻表的分析[J].人口与经济，2013,(2).

[7] 中国国家统计局.中国1990年人口抽样调查资料[M].北京：中国统计出版社，1992.

[8] 中国国家统计局.中国2000年人口抽样调查资料[M].北京：中国统计出版社，2002.

[9] 中国国家统计局.中国2005年1%人口抽样调查资料[M].北京：中国统计出版社，2007.

[10] 中国国家统计局.中国2010年人口抽样调查资料[M].北京：中国统计出版社，2012.