未决赔款准备金评估Clark方法及R实现

闫春，刘倩，刘伟

（山东科技大学a.数学与系统科学学院；b.计算机科学与工程学院，山东青岛266590）

0 引言

未决赔款准备金的提存对非寿险保险公司至关重要，其评估的精度将显著影响保险公司的业绩和经营的风险。随着时代的发展，相关研究逐渐的深入，未决赔款准备金评估的重点已从点估计转移到估计波动性与估计区间等其他统计特征。对原有确定性方法进行随机化改进，以便对准备金的损失过程建立随机模型，这种思路已经成为了如今准备金评估模型研究的主流[1-6]。本文研究的随机性方法基于Clark(2003)[7]，文中提出以最终赔付进展因子倒数的变化曲线模拟索赔损失进展趋势，建立随机模型并应用最大似然法求参数估计。该方法是一种能够对流量三角形的索赔进展趋势进行模拟的随机性方法，因此能够合理估计随机模型下的尾部因子，这一点是离散参数的随机模型(如广义线性模型)所不具备的。

本文首先介绍了Clark的建模思路与方法，给出该方法的模型结构与预测误差的计算公式。在保持原模型与结构误差不变的基础上，引入Bootstrap法，对样本与模型拟合值的残差进行重复抽样，从数值模拟的角度来度量模型参数误差的真值，给出Bootstrap法下模型评估未决赔款准备金的预测误差。最后，运用R软件将原方法的预测误差与Bootstrap法下的预测误差进行比较了算例的比较与分析。

1 Clark方法

1.1 Clark方法的基本假设

Clark建立的模型由两部分构成，一个是利用函数曲线对索赔损失的进展趋势做出合理的模拟；一个是假设每个进展期内发生的索赔是随机变量。即假设损失过程满足：

（1）各事故年累计索赔期望损失率的进展趋势均满足函数曲线G的表达式；

（2）增量索赔损失相互独立，同分布。

1.1.1 进展趋势的模拟曲线各事故年的索赔损失进展趋势曲线函数可表示为：

式(1)中LDFj即为同一事故年、不同进展年的最终赔付进展因子，即n为该事故年的最终进展年，且当j=n时，LDFn=1。所以有G(j)∈[0，1] j=1，…，n。不难发现，G(j)即是第j进展年时累计已决赔款占最终赔款的比例。

Clark参考Sherman(1984)[8]中运用反幂函数曲线拟合索赔损失进展趋势的结果，结合常用分布曲线的尾部特征，决定使用Loglogistic分布函数曲线与Weibull分布函数曲线。

采用Loglogistic曲线，有：

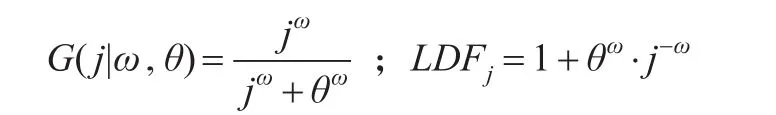
同理，Weibull曲线的表达式为：

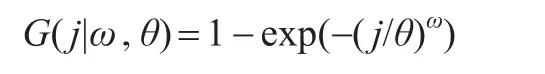
1.1.2 增量索赔损失的分布假设

设事故年i在第j个进展年的增量已决赔款Ci，j(1≤i≤I，1≤j≤J)为随机变量，其相互独立，服从过度分散泊松分布，则有：

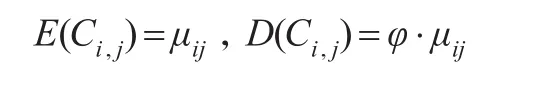
其中μij表示为事故年i在第j进展年间增量索赔损失的期望值，φ为OPD的散度参数，使用经调整的Pearson残差对其进行估计，其估计量为：

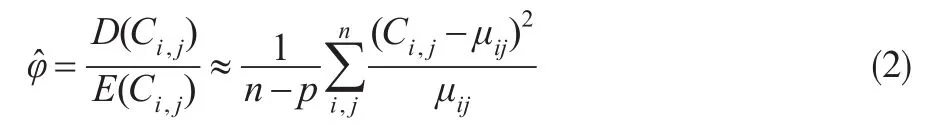
式(2)中p为模型参数个数，n为样本观察值。

做出两个假设后，还需求得各事故年的最终损失期望，才能够得到未来各个进展期索赔额的估计。Clark提出了分别基于LDF法与CapeCod法的思路利用最大似然法估计各事故年的最终损失，并建立了两种不同的评估模型。

1.2 LDF模型

LDF模型假设各事故年索赔的最终损失是相互独立的，增量索赔损失的期望表示为：

模型(3)中共有参数n+2个，其中包括n个事故年最终损失参数ULTi，两个模拟曲线参数ω，θ。

构建该模型的似然函数。由于增量已决赔款Ci，j相互独立，服从ODP分布（同负二项分布），以增量已决赔款流量三角形为数据样本，其对数似然函数为：

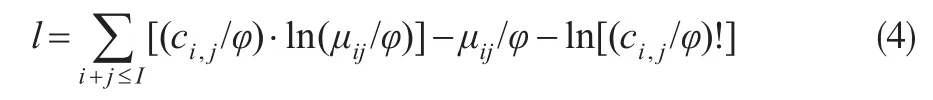
式(4)中的散度参数φ假设为未知常数。

对该模型进行极大似然估计（MLE）等同于对下式求极大：

将式(3)代入式(5)，得到：

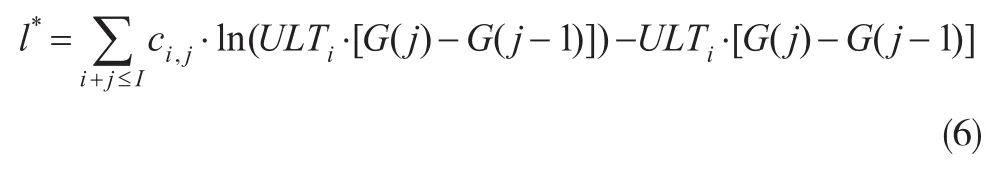
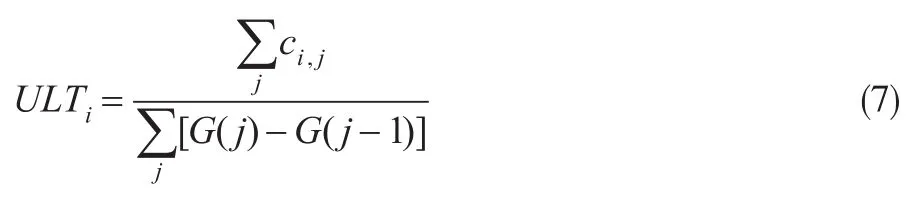
假设的拟合曲线不同，曲线参数ω与θ的MLE估计表达式也不同，这里不再详细给出。

1.3 Cape Cod模型

CapeCod模型假设历史时期内各事故年索赔的最终损失存在一定的联系，不妨认为各事故年的期望赔付率相同，即各事故年的已赚纯保费与最终损失期望的比值相同。其模型为：

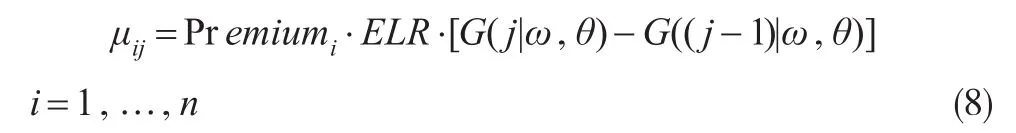
模型(8)中只有3个参数，分别为期望赔付率ELR和两个拟合曲线参数ω，θ。

构建该模型的似然函数。同LDF模型，其对数似然函数为式(4)。因此，对Cape Cod模型进行极大似然估计也等同于对式(5)求极大。

将式(8)代入式(5)，得到：

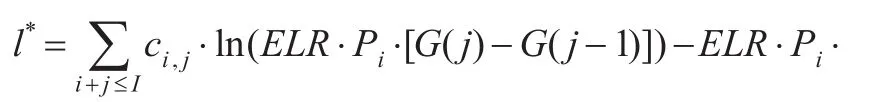
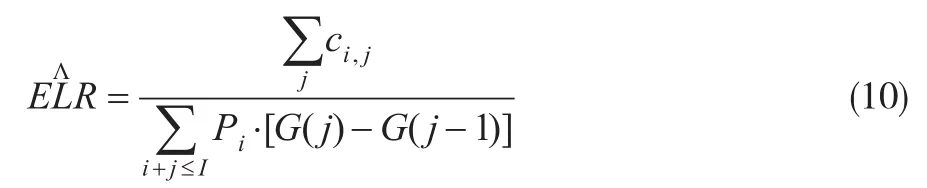
这里，ω与θ的MLE估计也不再详细给出。

求得各参数的MLE估计后，就可以得到增量已决赔款Ci，j的期望μij，总未决赔款准备金即为：

1.4 Clark方法的预测误差

随机模型的预测误差（MSEP）为：

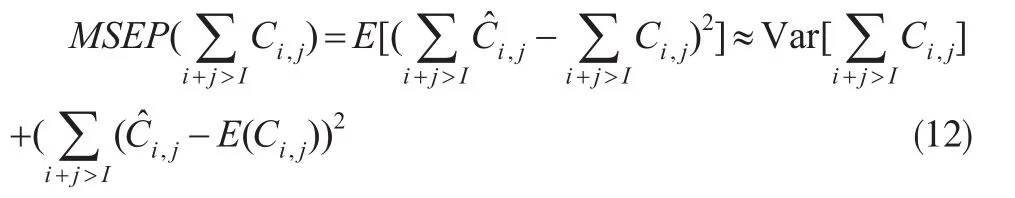
由式(12)可知，预测误差由过程误差与参数误差组成：过程误差是由随机假设部分造成，参数误差由曲线拟合部分造成。

在Clark方法下，考虑增量已决赔款Ci，j相互独立且服从过度分散泊松分布，则各模型的过程误差均为：

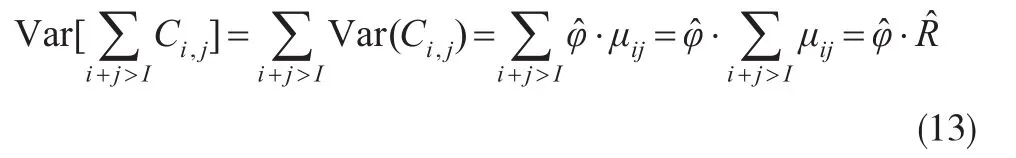
对于参数估计误差的计算，Clark使用Cramer-Rao信息不等式得到参数无偏估计的方差下界。

LDF方法下，Fisher信息矩阵为：

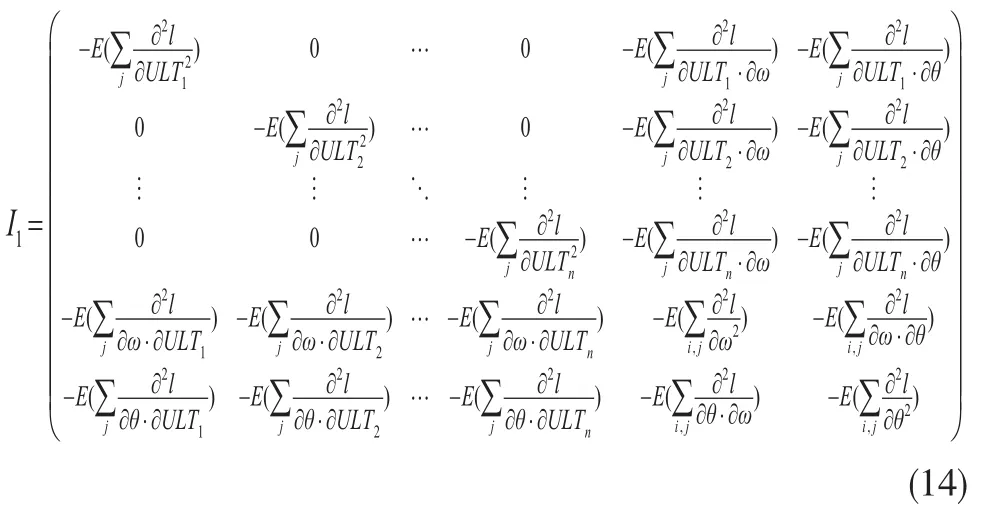
那么，参数估计的协方差矩阵满足：

其中：

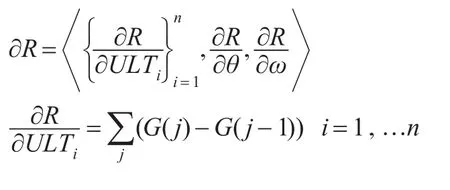
那么，其参数估计的协方差矩阵满足：

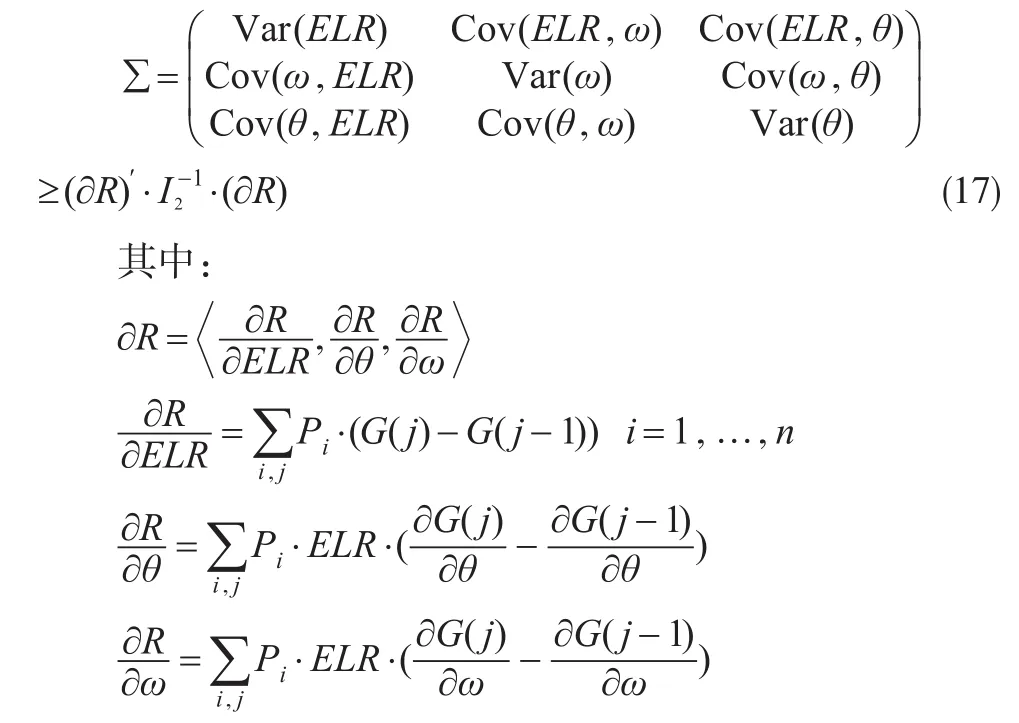
这样就得到了Clark方法下模型参数误差的度量，从而也就得到了预测误差。

这里应该指出，CapeCod模型与LDF模型比，参数误差会比较小。考虑包含10个事故年的流量三角形，运用CapeCod模型只需对3个参数进行估计，而LDF模型需要估计12个参数，因此LDF模型可能存在过度参数化的问题。

此时，本文得到的是参数无偏估计的方差下界，且当参数估计为一致最小方差无偏估计(UMVUE)时，方差就能够达到这个下界。但是这里必须要说明，Clark方法使用的MLE估计只是渐进无偏的，因此在样本容量不大的情况下，该方差下界只能作为一种近似的下界。这个近似的下界就作为Clark方法下模型参数误差的一个度量，最后将过程误差与其相加即得到Clark方法下模型的预测误差。

2 Bootstrap法在Clark方法中的应用

2.1 Bootstrap法模拟预测分布

依据Bjorkwall(2009，2011)[9,10]使用Bootstrap法给出未决赔款准备金预测分布的具体方法，应用参数Bootstrap法模拟Clark方法下准备金预测分布的基本思路为：

（1）在给定的增量已决赔款流量三角形数据样本下，按照Clark方法的建模思路求出模型参数的MLE估计，如LDF模型中的{，，进而得到{Ci，j}的拟合值与预测值，如：

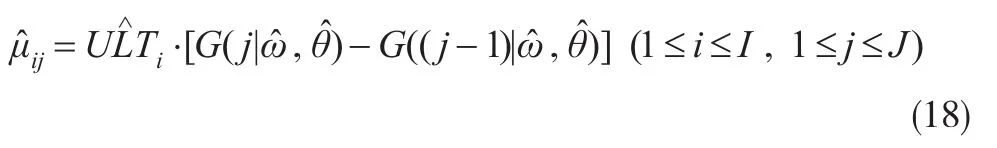
（2）计算分散参数φ，参考Clark方法中φ的估计，具体见（1）式。

（3）Clark方法中假设增量赔款额Ci，j服从ODP分布，因此，将第（1）步中的{Ci，j}的上三角形拟合值视为增量赔款随机变量Ci，j的均值，从均值为、方差为的ODP分布中抽取随机数，作为拟增量已决赔款流量三角形(i+j≤I)，然后在利用模型得到模拟数据下参数的MLE估计的预测值，如：

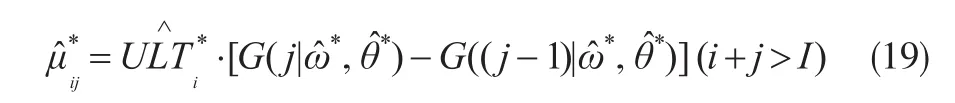
（5）多次Bootstrap再抽样，可得到总未决赔款准备金的预测分布的多次模拟，其样本点分布即为Bootstrap抽样下得到的总未决赔款准备金的预测分布。均值、标准差、分位数等相关分布度量都可以在样本点分布中求得。考虑到一般情况下，抽样10000次即可获得较满意的结果。

2.2 Bootstrap法估计预测误差

应用Bootstrap法求Clark方法的预测误差，实际上是用Bootstrap抽样数值模拟模型的参数误差。由式(13)，随机模型的预测误差为过程误差与参数误差之和，过程误差的计算见式(14)。

对于Bootstrap法求模型的参数误差，直接利用上文中的参数Bootstrap法计算未决赔款准备金预测分布过程中的结果。在多次重复抽样过程中，可以得到一系列未决赔款准备金的均值估计，Bootstrap法数值模拟的参数误差就是多次抽样得到的未决赔款准备金均值估计的方差(张连增(2008)[11])。

因此，Bootstrap法估计Clark方法的预测误差为：

相对于Clark根据信息不等式给出模型预测误差的一个近似下界，Bootstrap法则是利用统计推断对模型进行多次仿真来给出预测误差的数值模拟。应该说，这两种方法是各具优势的。由于Clark方法的参数估计不满足信息不等式的使用条件，原方法给出的预测误差只是一个真值取值的近似下界，因此本文引入Bootstrap法给出参数误差的数值模拟，这样可以从另一个角度给出预测误差真值的度量，使得精算人员对Clark方法下模型的预测误差有更准确的认识。

3 实证分析

本文利用Taylor&Ashe(1983)[12]文中的数据样本进行实证分析。该样本在张连增[3]、Clark[7]等学者的文中均被引用为算例，其每一事故年的索赔进展趋势都比较平稳，利于分析。具体样本数据见表1所示。

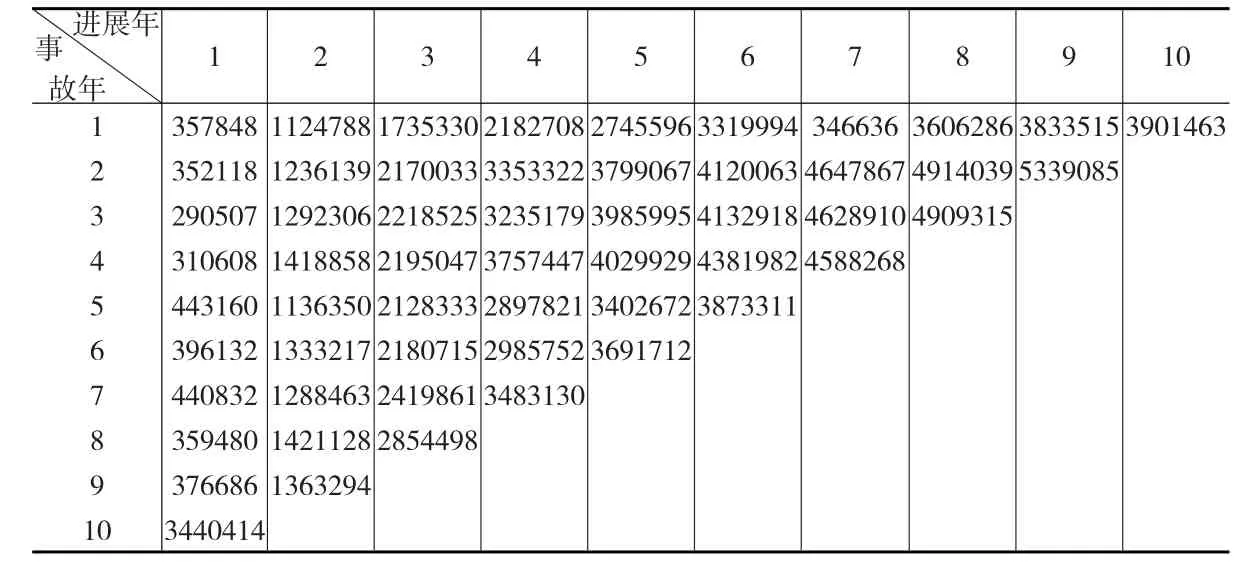
表1 累计已决赔款额流量三角形

使用R软件中ChainLadder程序包，即得到样本下LDF模型与CapeCod模型的相关估计结果。由于CapeCod模型的建立需要各事故年已赚纯保费数据，因此参考Clark的处理方法：在该流量三角形数据样本下，假设各事故年已赚纯保费是线性递增的，满足：Pi=10000000+400000×(i-1) i=1，…，10。Clark方法能够模拟索赔损失的进展趋势，在仅有10年索赔数据的情况下，也可利用曲线外推得到最终赔付损失。考虑未来的不确定性，本文对每个模型都外推10年。各模型估计结果见表2所示。

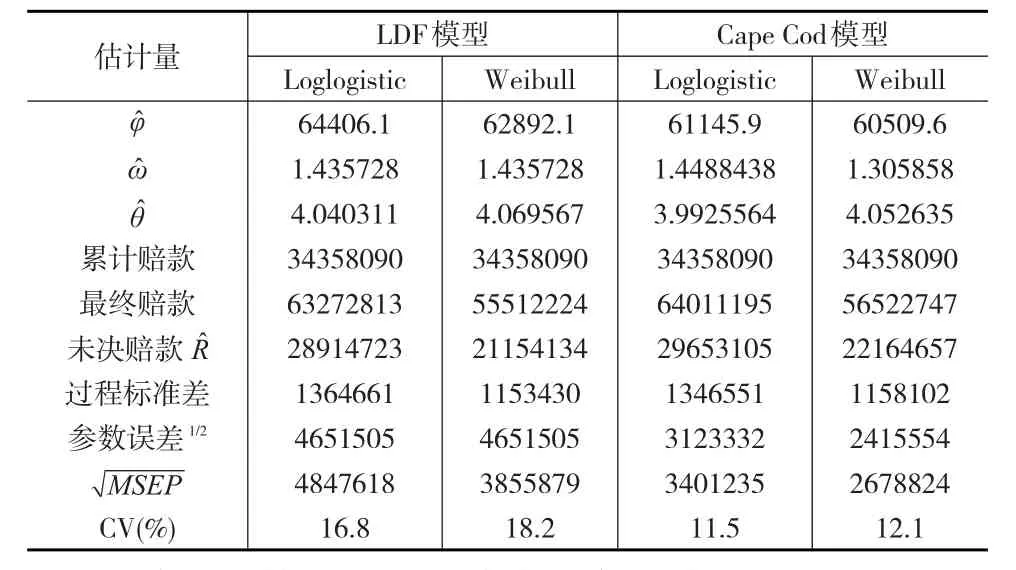
表2 Clark方法下各模型的参数及误差估计

观察同一模型下不同曲线拟合的结果，可以发现Loglogistic曲线下的准备金、预测误差都比Weibull曲线的大。造成这种情况的主要原因是因为Loglogistic分布是重尾分布，而Weibull分布的尾部较Loglogistic分布“薄”。虽然精算人员在评估未决赔款准备金时都比较保守，但是Loglogistic曲线模型也有其研究意义。由于未来的不确定性，任何合理假设建立的评估模型都有其参考价值。精算人员在预感到未来可能会出现大量理赔的情况下，使用Loglogistic这样的重尾分布曲线就非常合理。

观察两个模型的过程误差，可以发现LDF模型与CapeCod模型大致相同。对于参数误差方面，LDF模型则比CapeCod模型大了许多。这可能是因为CapeCod模型建模时使用了更多的索赔信息数据，有效降低了参数误差。因此，尽可能多的将索赔信息考虑进模型中对减少模型的预测误差、提高评估精度是十分有效的，从最后的CV值情况来看也支持这个结果。但是我们同样也不能认定CapeCod模型要优于LDF模型，因为两者建模时利用的信息不对等，CapeCod模型的估计结果优于LDF模型在一定程度上是必然的。而且，相对于CapeCod模型，LDF模型的建立更具有一般意义，该模型是以链梯法思想为基础，可以与其他基于链梯法思想的随机模型进行比较分析，体现Clark方法的特点。

运用Bootstrap抽样，得到的各模型参数Bootstrap法下参数误差及MSEP见表3所示。

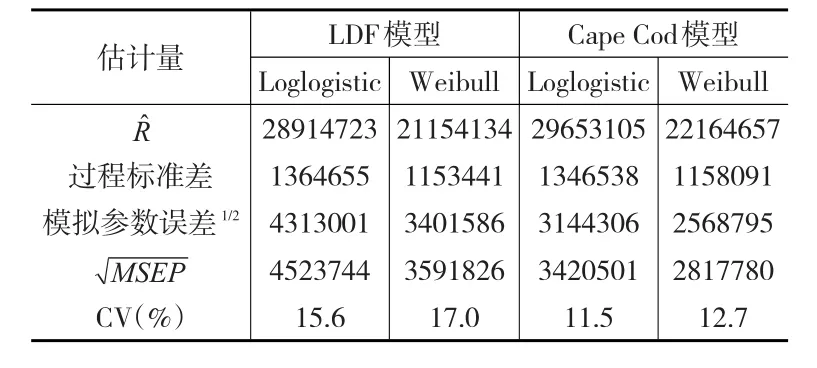
表3 Bootstrap法下各模型的估计误差

从表3可以看出，各模型Bootstrap法下的参数误差与MSEP大小的排序与信息不等式给出的结论是一致的：采用Weibull曲线的模型比Loglogistic曲线模型的误差要小；CapeCod模型的预测误差比LDF模型的要小。

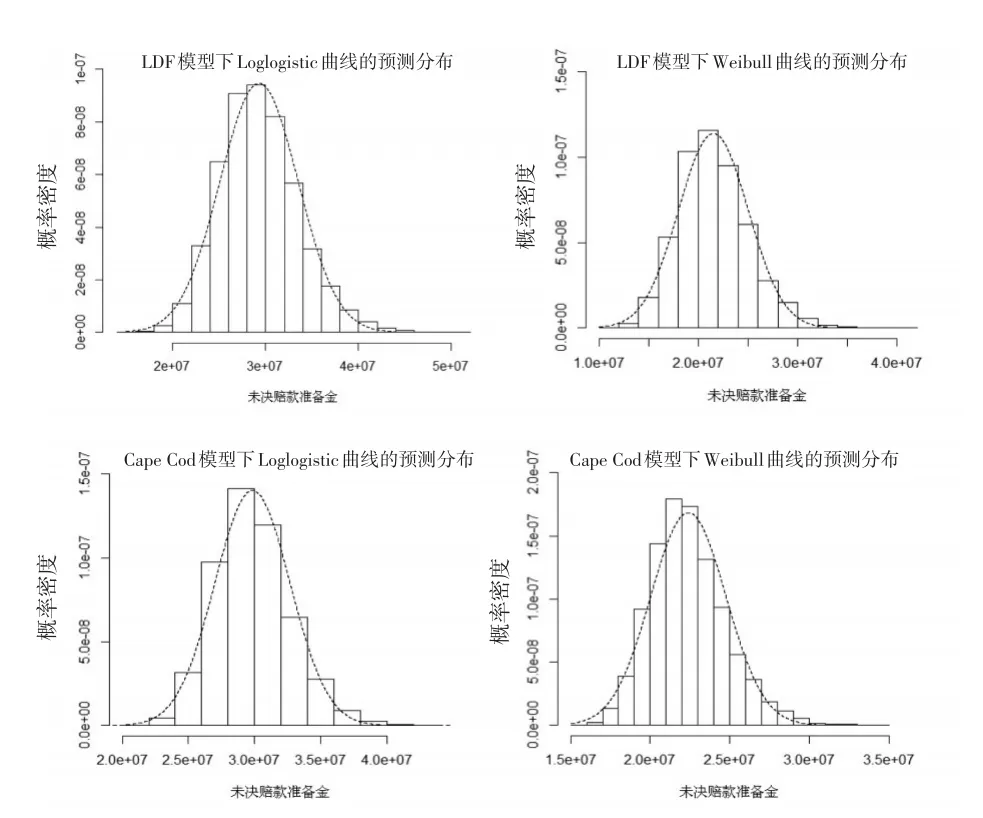
图1 参数Bootstrap法下各模型评估未决赔款准备金的预测分布

图1给出的是利用参数Bootstrap法模拟得到的Clark方法下四个模型评估总未决赔款准备金的完整预测分布，其对应的分布特征见下页表4。在大量重复抽样的情况下，总未决赔款准备金的预测分布呈渐进正态，本文分别给出了对应的正态分布曲线，各模型的预测分布曲线对比见下页图2。

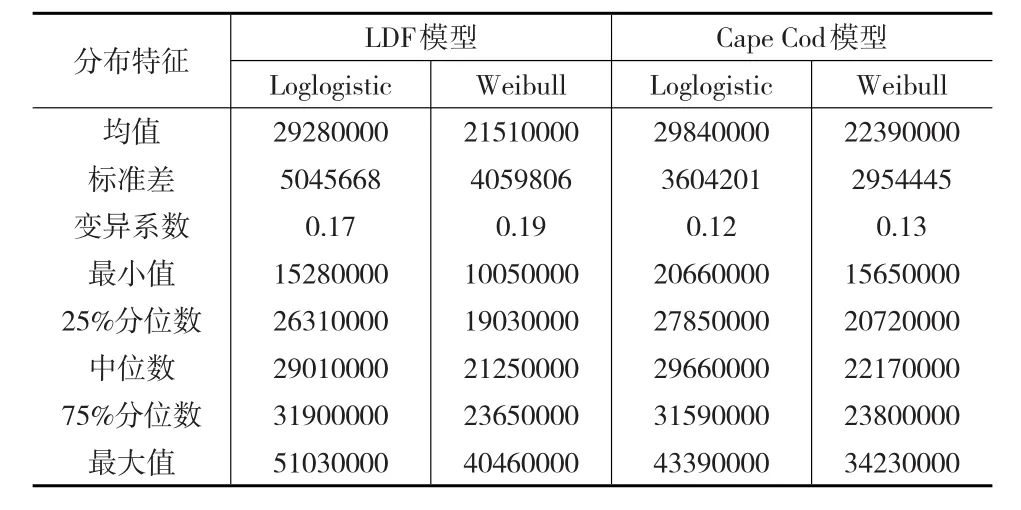
表4 参数Bootstrap法下未决赔款准备金预测分布的分布特征

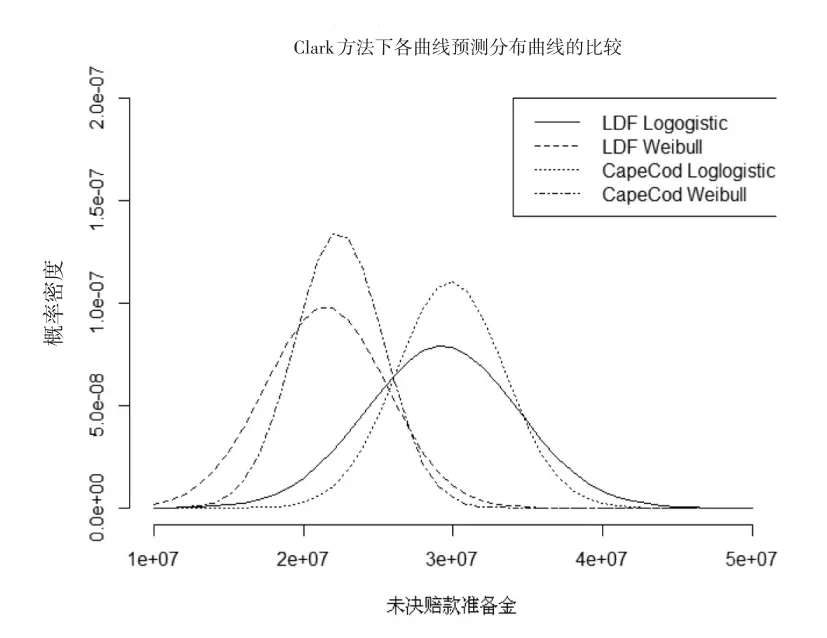
图2 各模型评估未决赔款准备金的预测分布拟合曲线的比较

4 结论

本文研究了未决赔款准备金评估的Clark方法，并在此基础上做了进一步的探讨。Clack方法利用分布函数曲线来模拟索赔损失的进展趋势，在假设增量已决（已报案）赔款服从过度分散泊松分布的情况下，使用最大似然法对各事故年最终损失和分布曲线中的参数进行估计，并利用信息不等式给出预测误差的近似下界。该方法是一种可以对损失进展趋势进行模拟并估计尾部因子的随机性评估方法，这是该方法的独特之处，也是本文研究该方法的主要原因。考虑原方法中计算未决赔款准备金预测误差的方法有条件限制且过于复杂繁琐，本文引入了Bootstrap法相关理论，从数值模拟的角度得到预测误差的一个度量，并给出该方法下未决赔款准备金的预测分布。最后，本文对两种方法做了理论与算例的比较，分析了各自的特点与优势。

[1] 张连增,段白鸽.准备金评估的随机性Munich链梯法及其改进[J].数量经济技术经研究,2011,(11).

[2] 张连增,段白鸽.基于Bootstrap方法的随机性准备金进展法及R实现[J].山西财经大学学报,2011,33(4).

[3] 张连增,段白鸽.基于GLM的未决赔款准备金评估的随机性链梯法[J].财经理论与实践,2012,33(1).

[4] Martinez M D,Nielsen J P,and Verrall R J.Double Chain Ladder[J].ASTIN Bulletin,2012,42(1).

[5] Martinez M D,Nielsen J P,and Verrall R J.Double Chain Ladder and Bornhutter-Ferguson[J].North American Actuarial Journal,2012,16(2).

[6] 钱晗.改进Bootstrap方法在未决赔款准备金估计中的应用[D].吉林：吉林大学硕士论文,2014.

[7] Clark D R.LDF Curve-Fitting and Stochastic Reserving:A Maximum Likelihood Approach[J].CAS Forum,2003,(3).

[8] Sherman R.Extrapolating Smoothing and Interpolating Development Factors[C].Proceedings of the Casualty Actuarial Society,1984.

[9] Bjorkwall S,Hossjer O,Ohlsson E.Non-parametric and Parametric Bootstrap Techniques for Age-to-Age Development Factor Methods in Stochastic Claims Reserving[J].Scandinavian Actuarial Journal,2009,(4).

[10] Bjorkwall S,Hossjer O,Verrall R J.A Generalized Linear Model With Smoothing Effects for Claims[J].Insurance:Mathematics and Economics,2011,49(1).

[11] 张连增.未决赔款准备金评估的随机性模型与方法[M].北京:中国金融出版社,2008.

[12] Taylor G,Ashe F R.Second Moments of Estimates of Outstanding Claims[J].Journal of Econometrics,1983,(23).