双边公平匹配决策方法及其应用

赵焕焕，菅利荣，刘勇

（1.南京航空航天大学经济与管理学院，南京211106；2.无锡职业技术学院管理学院，江苏无锡214121；3.江南大学商学院，江苏无锡214122）

0 引言

现实生活中存在大量的匹配问题，为有效解决此类问题，Gale和Shapley[1]针对婚姻问题提出了匹配理论，随后Roth等[2]提出双边匹配的概念，界定了“双边匹配”和“双边”的概念，并给出一些求解匹配的算法[3]，将其应用到医院与实习生的双边匹配、入学学生与学校的双边匹配、风险投资商与风险企业匹配等领域[4]。

为发展和完善双边匹配理论，专家、学者从不同的角度以不同的研究问题为背景，基于经济学和决策科学等理论与方法构建相应的双边匹配方法和模型。由于本文主要探讨的决策问题，因此，本文重点关注基于决策科学的匹配方法，其主要是利用证据理论、集结算子等方法，行为经济科学等构建杂合匹配模型，进而探究双边匹配满意度[5,6]、匹配主体的心理行为[7,8]、匹配稳定性[9,10]、匹配算法[9]等。通过梳理发现，双边匹配决策的研究大多是从匹配主体的满意度或稳定性角度探讨匹配问题，缺乏从匹配主体的满意度和匹配方案的公平性与稳定性整体探究。考虑到稳定性、公平性和满意性是衡量匹配方案优劣的重要依据，直接影响和决定着匹配决策的质量和效率，本文构建了一种双边公平稳定匹配决策方法。

1 双边匹配决策模型

在双边匹配决策问题中，设A={a1，...，ai，...，am}、B={...，bj，...，bn}分别为有限非空甲、乙方主体集合，其中，m≥2，ai(i=1，2，...，m)为第i个甲方主体，n≥2，bj(j=1，2，...，n)为第j个乙方主体。一般来说，甲方主体ai对乙方主体bj的偏好程度是基于多方面考虑而获得，设评价属性集合为C={...，ck，...，cp}，ck为第k个评价属性，aijk为甲方主体ai对乙方主体bj关于属性ck的属性值；wk(k=1，2，...，p)为属性ck的权重，且方主体bj对甲方主体ai的偏好程度可从属性集合D={...，dt，...，dq}进行测度，dt为第t个评价属性，bijt为匹配对象ai对匹配对象bj关于属性dt的属性值；ηt(t=1，2，...，q)为属性dt的权重，且考虑到客观世界的复杂性、不确定性，匹配评估属性值往往以区间数给出，即aijk∈[]和bijt∈。

定义1[4]：设μ:A∪B→A∪B为一种法则，对于∀ai∈A，∀bj∈B，如果满足μ(ai)=bj或μ(bj)=ai，则分别称μ(ai，bj)为甲、乙方主体的匹配方案和匹配对。

注：μ(ai)=bj表示在μ中甲方主体ai与乙方主体bj形成匹配，而μ(ai)=ai和μ(bj)=bj分别表示在μ中甲方主体ai和乙方主体bj未有乙方主体和甲方主体与其匹配。根据μ确定的所有匹配对的集合称为匹配方案μ。

对于甲方主体ai和乙方主体bj，其能否形成匹配主要依据彼此对对方的满意程度。通常，甲方主体ai和乙方主体bj形成匹配是由于双方对彼此的满意度达到或超过其设定的阈值，满意度越高，两方主体所形成的匹配就越稳定，匹配方案也越好。设αij表示甲方主体ai对乙方主体bj的总体满意度；βij表示乙方主体bj对甲方主体ai的总体满意度。

考虑甲乙主体的不同满意度和双方匹配地位的公平性，可用甲乙双方主体对匹配方案或匹配对象满意度的偏差描述和测度。鉴于此，可定义匹配主体的公平性匹配方案。

定义2[4]：设μ={...，μs，...，μl}表示由匹配主体集合A和B确定的所有匹配方案的集合，对于μs表示μ中的第s个匹配方案，如果匹配对(ai，bj)的匹配主体对彼此的偏好程度偏差为：

则称μs称为双边主体公平匹配方案。

其中，s=1，2，...，l，μs=аrg min{f(μ1)，...，f(μs)，....，f(μl)}。

如果f(μs)=0，则μs为双边主体绝对公平的匹配方案。

甲方主体ai和乙方主体bj能否形成配对在于双方对彼此的满意度。对于甲方主体ai和乙方主体bj，由于满意度最大时，其与各自理想匹配对象的距离为0。鉴于此，可利用各匹配对象与理想匹配关于属性集合的距离测度匹配对象ai和bj对彼此的满意程度。考虑到灰靶决策是根据靶心距离的大小测度对象的优劣[11]，下面定义理想匹配对象，并利用靶心距离定义匹配距离，测度甲乙双方对彼此的满意度。

定义3：对于∀ai∈A，∀bj∈B，如果有则分别称：

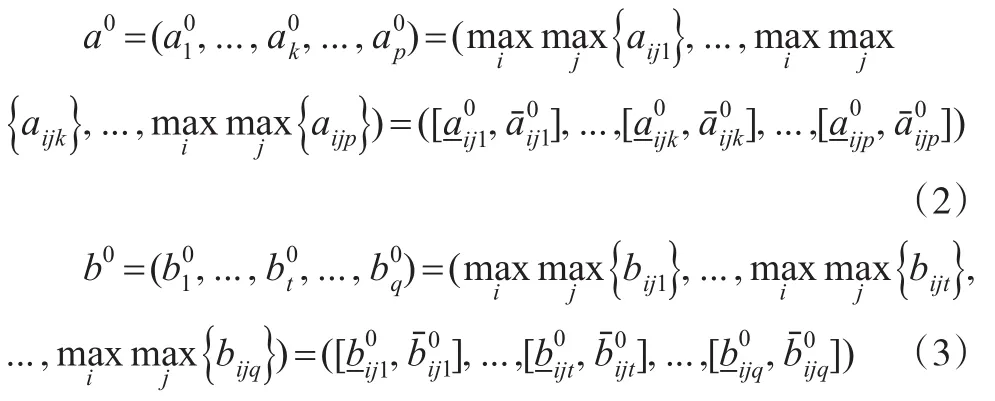
为匹配群体A和B的理想匹配对象。

其中，i=1，2，...，m;j=1，2，...，n;k=1，2，...，p;t=1，2，...，q。

根据上面的定义，对于匹配对象ai和bj，与理想匹配对象a0和b0关于属性集C和D越接近，可知，其分别对匹配bj和ai的满意度就越高；反之，满意度较小。

定义4：对于∀ai∈A，∀bj∈B(i=1，2，...，m;j=1，2，...，n)，如果

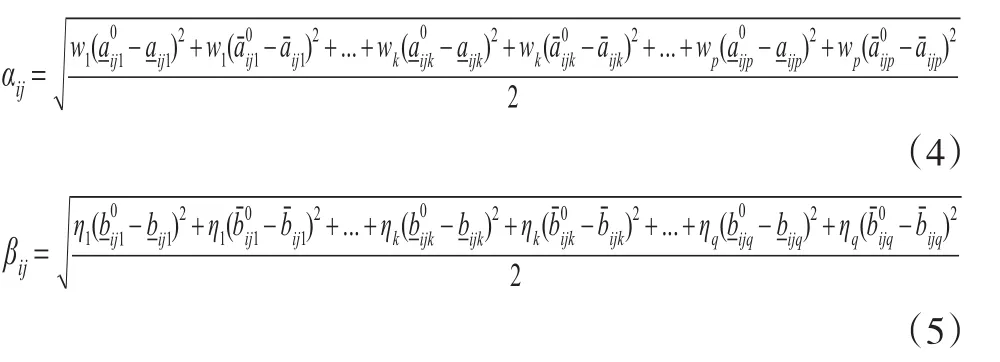
为甲方主体ai和乙方主体bj与其理想匹配对象的匹配距离。

根据定义4可知，对于甲方主体ai，其与他的理想匹配对象的距离越小，其对乙方主体bj越满意；对于乙方主体bj，其与其理想匹配对象的距离越大，表明满意度越低。一般匹配主体或匹配系统均存在一个满意度临界值，即匹配距离阈值，设λ＞0表示匹配系统主体的匹配距离阈值。考虑到本文是用匹配距离刻画匹配主体的满意度，其与满意度呈现反向关系，如果αij＜λ，表示甲方主体ai认为乙方主体bj是可接受的；βij＜λ，表示乙方主体bj认为甲方主体ai是可接受的。在匹配方案中，当μ(ai)=ai，记甲方主体ai的满意度αij≥λ；当μ(bj)=bj，记乙方主体bj的满意度βij≥λ。

设xij决策变量，其中，xij∈{0，1}，如果xij=1，则表明甲方主体ai与乙方主体bj完成匹配；xij=0为未匹配。鉴于各主体与理想匹配对象的距离越小，其对双方主体的满意度越高，并考虑到匹配的稳定性与公平性，依据甲方主体ai对乙方主体bj的匹配距离矩阵和乙方主体bj对甲方主体ai的匹配距离矩阵可建立基于距离最小和距离偏差最小的多目标优化模型，如下所示：

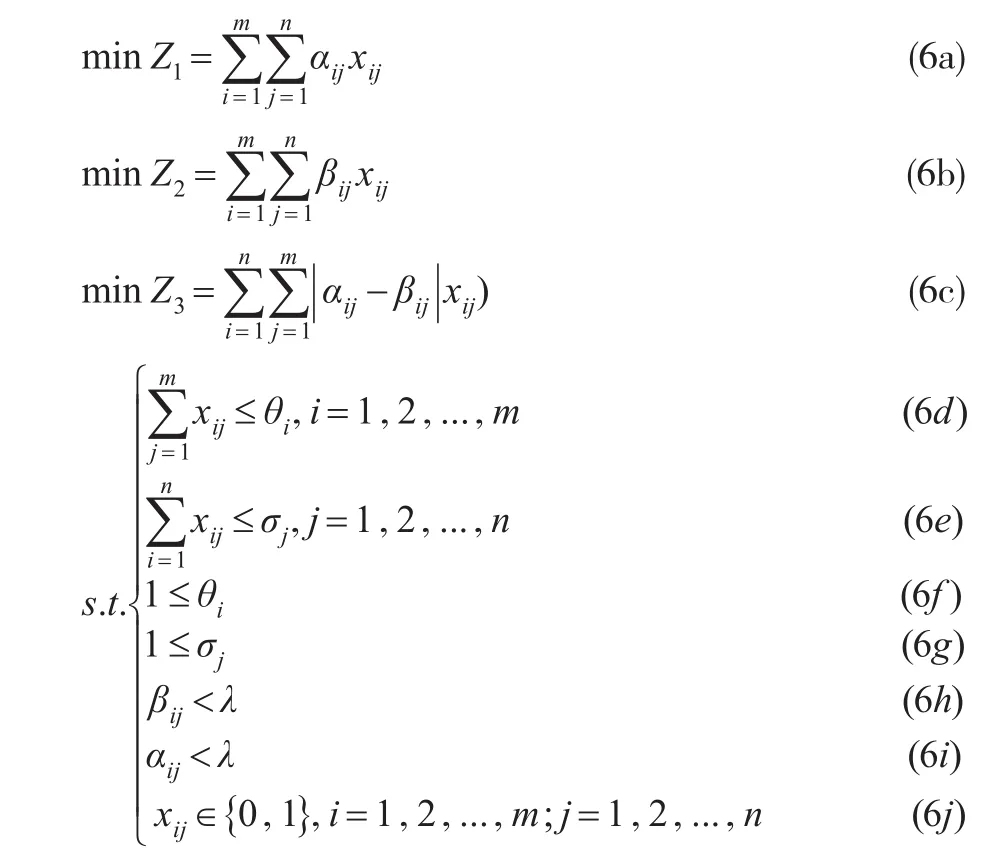
其中，式（6a）至式（6c）为目标函数，式（6a）表示最小化所有甲方匹配主体对乙方的距离之和；式（6b）表示最小化所有乙方匹配对甲方主体的匹配距离之和；式（6c）表示甲方主体ai和乙方主体bj在匹配过程中匹配方案的公平性；式（6f）至式（6g）中ci，dj的含义为甲、乙主体ai和bj最多能匹配的对象个数；式（6h）至式（6i）表示甲方与乙方主体的满意度需要满足阈值。

对于上面的多目标优化模型，利用模拟植物生长算法[12,13]求解多目标最优匹配方案。

2 案例分析

本文用经济因素、保障因素、发展因素、环境因素4项8个指标构成农民工决策评价指标。其中,经济因素主要是指企业提供的薪酬情况；保障因素主要是指福利待遇、参加社会保险情况；环境因素主要是指人际关系、身份认同等方面的情况；发展因素主要是指技能培训、发展空间等方面的情况。用劳动力成本、劳动者素质、发展潜力、个性特征4项8个指标构成企业（岗位）决策评价指标。其中劳动力成本主要指劳动者期望薪金要求；专业技能主要指农民工教育情况、专业技能、工作经验等；个性特征主要劳动者忠诚度、吃苦精神等；发展潜力主要指沟通能力、团队精神等。

为进一步研究农民工和企业岗位的匹配情况，选择江苏省无锡市30家招用农民工较多企业人力资源部的工作人员通过电子邮件、传真等各种方式，向被调查对象发送问卷,请他们根据自身的专业知识和实践经验完成从这8个初始指标中挑选出认为应该保留的指标。同时，在企业和劳动力市场，随机选取80个农民工通过问卷调查的方式，完成从这8个初始指标中挑选出认为应该保留的指标。整个调查历时半个月,共收回企业调查问卷28份,有效问卷26份,回收率和有效率分别达到了93%和86%；收回农民工调查问卷77份，有效问卷75份，回收率和有效率分别达到了96%和93%；收回政府就业管理部门调查问卷12份，有效问卷12份，回收率和有效率均为85.7%。最后，采用隶属度分析方法，删除初设指标与评价目标不相关、重要程度低或不具有可操作性的指标，农民工评价岗位的评价指标薪酬待遇、福利保障、工作环境、发展空间，将其分别记为C={C2，…，C4}；而企业评价农民工主要为期望薪金要求、相关行业工作经验、专业技能、吃苦精神、忠诚度5个评价指标，将其记为D={d1，d2，…，d5}。无锡市某天人才市场收到6个农民工（分别记为a2，a3，a4，a5，a6）和4个企业（分别记为b1，b2，b3，b4）需求申请，经过调研分析和数据整理，可得农民工和企业岗位互评属性值，如表1和表2所示。

综合调查访谈的结果和相关专家的意见，整理可得农民工评价属性权重为wk=(0.3,0.2,0.22,0.28)；企业评价属性权重为ηt=(0.25,0.18,0.15,0.2,0.22)；企业和农民工最低匹配距离不得高于或者等于0.2，即λ=0.2；只要企业2和企业3最多招两名人员，而其他最多招一名人员，即θ1=θ2=...=θ6=1，σ1=σ3=2，σ2=σ4=1。

根据企业岗位与农民工互评的属性值，利用公式（2）和公式（3）计算，可确定各匹配主体关于属性集合的理想匹配对象，其分别为：

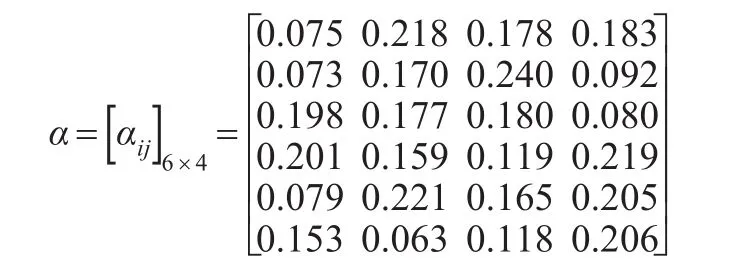
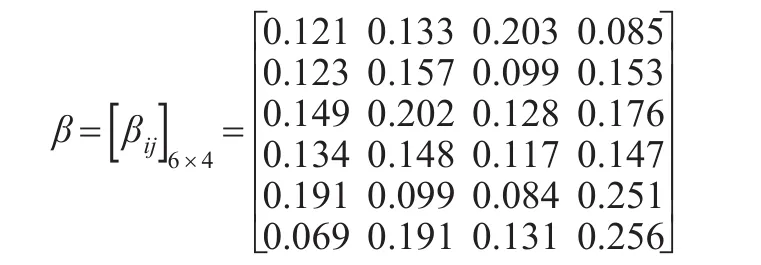
根据企业岗位与农民工的满意系数，企业评价指标权重分别为0.25,0.18,0.15,0.2,0.22，农民工评价指标权重分别为0.3,0.2,0.22,0.28，利用公式（4）和公式（5），可求得企业岗位与农民工关于属性对彼此的匹配距离，可得企业岗位与农民工互评匹配距离，相应地，可确定农民工A对岗位B的匹配矩阵和岗位B对农民工A的匹配距离矩阵，其分别为：

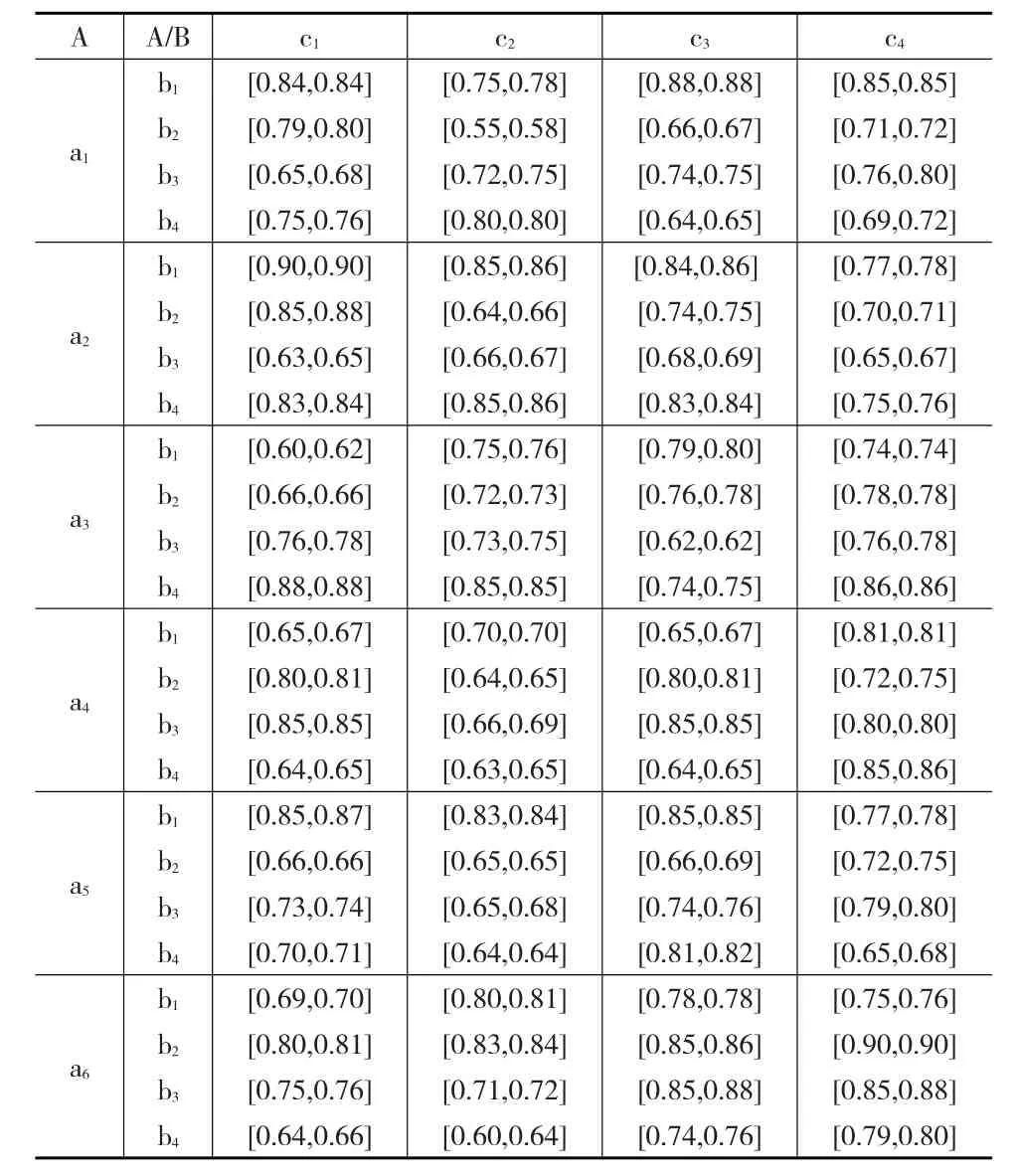
表1 农民工对企业岗位的评价信息

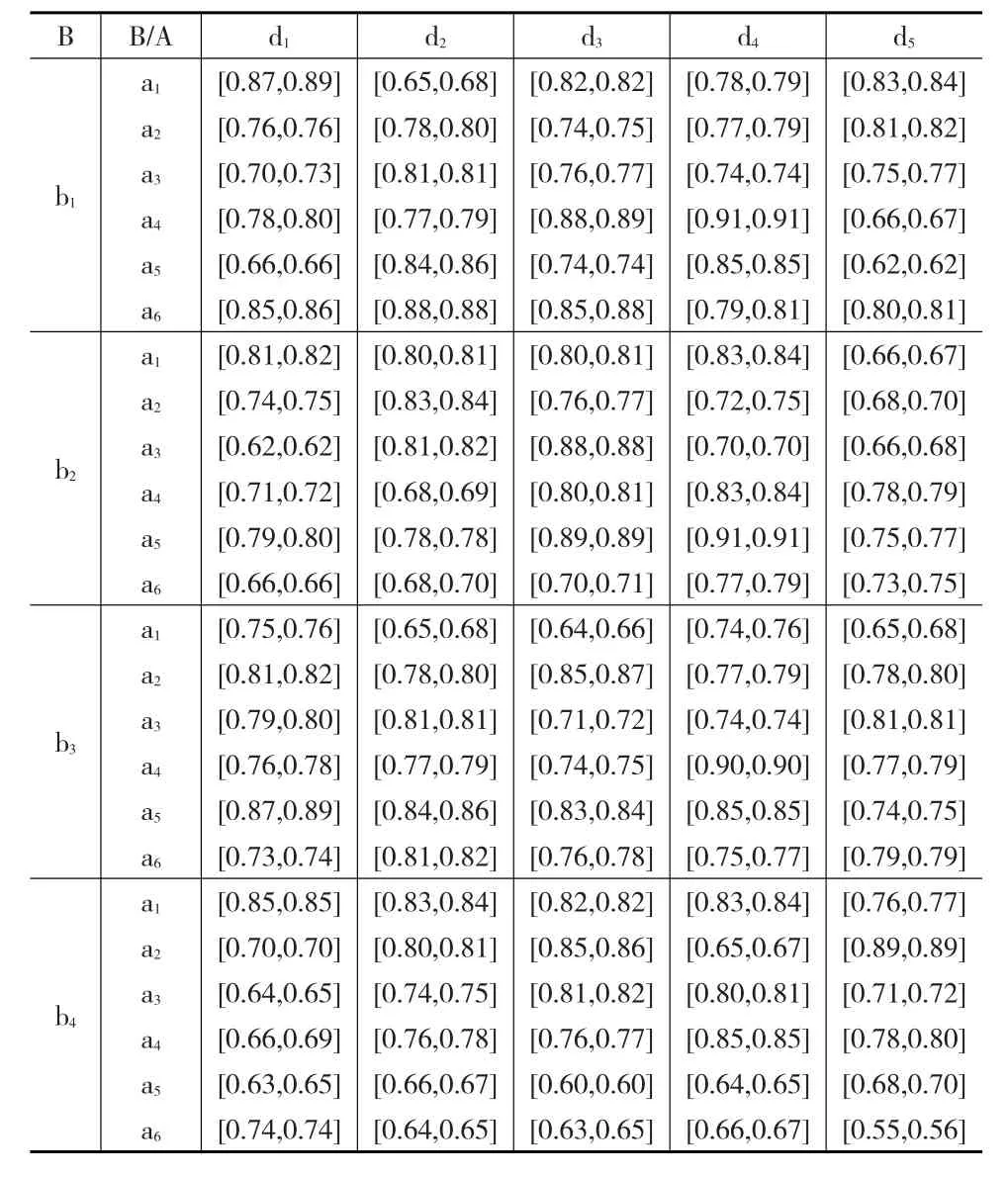
表2 企业对农民工的评价信息

根据农民工和岗位互评的匹配距离矩阵，可构建最优化模型（6），采用植物生长模拟算法利用MATLAB15.0求解上式多目标优化模型，可得最优匹配方案，其匹配结果如下：(a1，b1)，(a2，b1)，(a3，b4)，(a4，b3)，(a5，b3)(a6，b2)。由匹配结果可知，所有农民工均实现了就业，而企业也找到了相对合适企业的人员。基于计算案例可知，所构建的模型充分考虑匹配主体偏好和匹配方案的稳定性与公平性，能够很好地描述和解决农民工就业匹配问题，更符合参与各方的理想选择，因而具有较强的稳定性和可操作性。通过模型求解分析，其经济因素依然是影响农民工就业匹配的重要因素，当双方在工资福利方面的满意度差距不大时，最终实现匹配的可能性较大。从2012年开始我国劳动年龄人口开始出现了绝对数量的下降，根据人口发展规律，未来较长时期我国劳动年龄人口还将继续下降。随着我国“人口红利”逐步消失并由此导致了农民工在劳动力市场上工资议价能力的提升，因此，解决农民工就业匹配问题，首先要解决农民工工资收入过低的问题。同时，也要看到要非经济因素对农民工就业匹配的影响正在加大。从计算结果表明：匹配成功的6对组合在经济因素上不存在一一对应的关系，说明农民工就业选择已从追求工资福利待遇等物质需求为主，转向经济、保障、发展、环境等其他因素的综合考量。

3 结论

为有效描述和解决双边匹配决策问题，构建一种双边公平匹配决策模型。通过模型和案例分析，结果表明所构建的模型能够很好地描述双边匹配决策问题，并且与已有方法相比，模型不仅考虑了匹配方案的稳定性，更关注了匹配的公平性和满意性，能够为解决现实中基于多属性评价信息的双边匹配问题提供借鉴。

[1] Gale D,Shapley L.College Admissions and the Stability of Marriage[J].American Mathematical Monthly,1962,69,(1).

[2] Roth A E.Common and Conflicting Interests in Two-Sided Matching Markets[J].European Economic Review,1985,27,(1).

[3] Roth A E.New Physicians:A Natural Experiment in Market Organiza⁃tion[J].Science,1990,250,(4987).

[4] 刘勇,熊晓璇,全冰婷.基于灰色关联分析的双边公平匹配决策模型及应用[J].管理学报,2017,14(1).

[5] 李铭洋,樊治平,乐琦.考虑稳定匹配条件的一对多双边匹配决策方法[J].系统工程学报,2013,28(4).

[6] 樊治平,乐琦.基于完全偏好序信息的严格双边匹配方法[J].管理科学学报,2014,17(1).

[7] 李铭洋,樊治平.考虑双方主体心理行为的稳定双边匹配方法[J].系统工程理论与实践,2014,34(10).

[8] 陈希,韩菁,张晓.考虑心理期望与感知的多属性匹配决策方法[J].控制与决策,2014,29(11).

[9] 魏立佳.弱偏好序下的最优单边匹配算法设计[J].系统工程理论与实践,2011,31(9).

[10] Afeche P A,Diamant J M.Double-sided Batch Queues With Aban⁃donment:Modeling Crossing Networks[J].Operations Research,2014,62,(5).

[11] Liu S F,Lin Y.Grey Information Theory and Practical Applications[M].London:Springer-Verlag,2011.

[12] 李彤,王春峰,王文波等.求解整数规划的一种仿生类全局优化算法——模拟植物生长算法[J].系统工程理论与实践,2005,25(1).

[13] 李彤,王众托.模拟植物生长算法与知识创新的几点思考[J].管理科学学报,2010,13(3).