具有禁止子图的有向图是超欧拉有向图的条件

郑焕，董畅畅

(新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017)

0 引 言

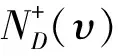
Boesch,Suffel和Tindell[2]在1977年提出了超欧拉问题,他们致力于刻画出包含生成欧拉子图的无向图,同时,他们表示这个问题是非常困难的.Pulleyblank[3]在1979年证明了判定一个无向图(甚至包含平面无向图)是否是超欧拉的是NP-完全的.截至今日,已经有大量关于超欧拉无向图的研究,例如Catlin的研究[4]和他的更新版[5].

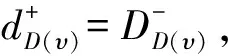
禁止诱导子有向图一直是被广泛研究的话题.给定一个有向图K和一个有向图D,如果对于D的任意一个子图H,若满足H≌K,则|A(D〈V(H)〉)|>|A(H)|+1,则称D不含K子图.一直在被深入研究的是成为哈密顿的充分条件是不含K1,3子图,可以参考[10].

1 主要结论

如果D是非哈密尔顿的,但是强连通的,则在D中存在至少一个S-路或S-圈.A.Kemnitz和 B.Greger给出了定理1中的结论.

定理1[10]如果R是一个至少有3个点的定向图且不含图1中的诱导子图,则称R是哈密尔顿有向图.

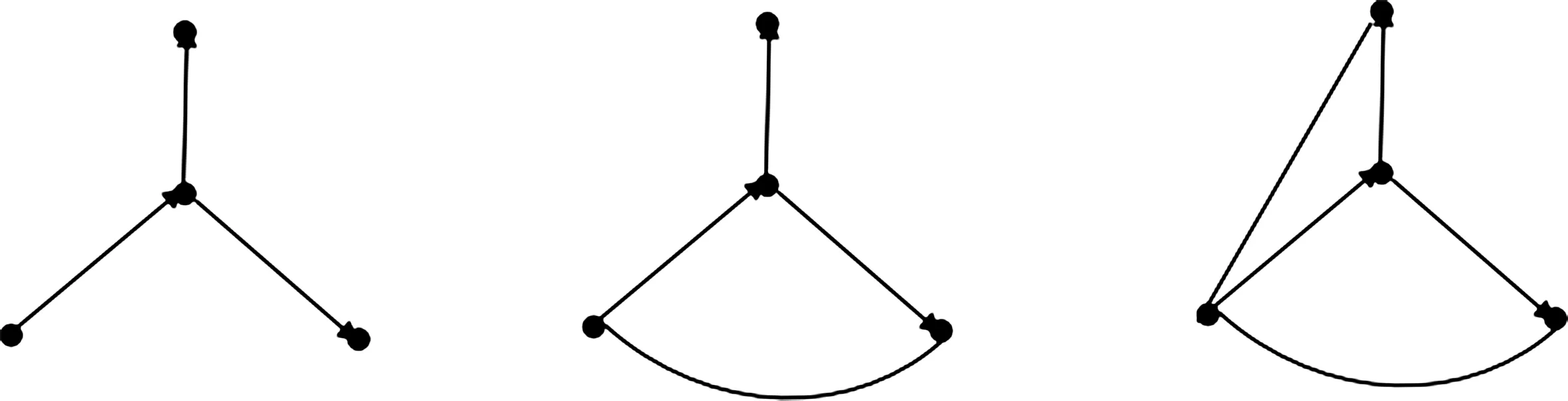
图1 禁止诱导子图注：图1中未标方向的弧可以看作是任意方向

在定理1中,A.Kemnitz和 B.Greger证明了含有禁止诱导子图的定向图是哈密尔顿的其中一种情况,有这个结论我们可以得到推论1.

推论1设R是一个至少有3个点的定向图,如果R不含图2中的诱导子图,则称R是哈密尔顿有向图.

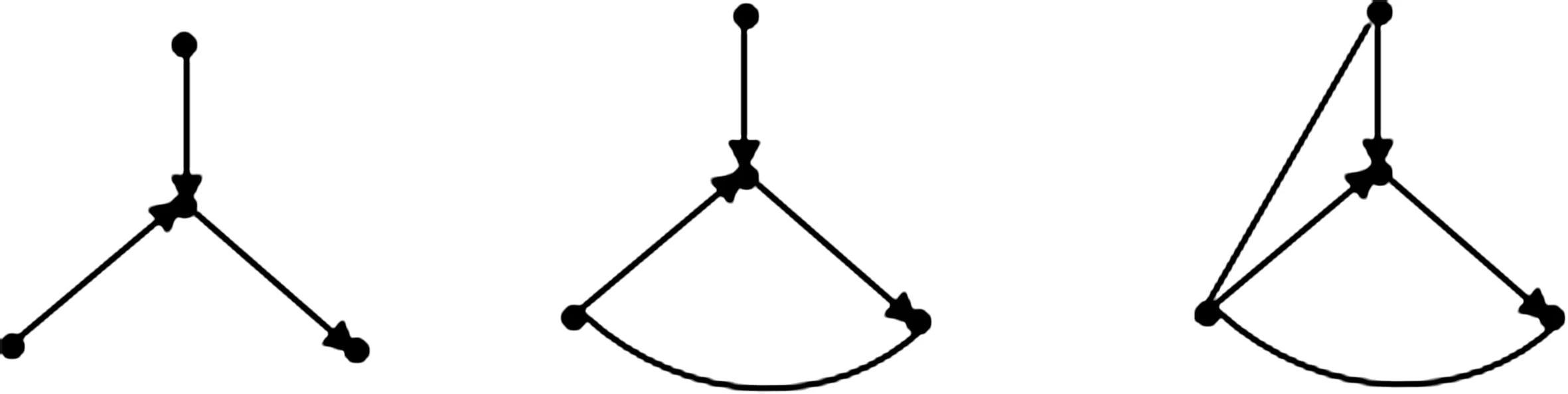
图2 禁止诱导子图注：图2中未标方向的弧可以看作是任意方向

证：假设R满足推论中的条件,但是非哈密尔顿有向图.

令S=(v1,v2,…,vn,v1)是有向图R中长度最大的有向圈.因为R强连通但非哈密尔顿有向图,所以在有向图R中存在一个S-路或S-圈.

情形1. 如果R中没有S-路,则一定存在一个S-圈C.令vk是S和C公共点,ur在C中是vk的上升点(见图3).因为在R中没有S-路,故点vk-1和点vk+1都是与ur不相邻的点.因而,R({vk-1,vk,vk+1,vr})是R的诱导子图也是图2中的第一种或第二种类型.

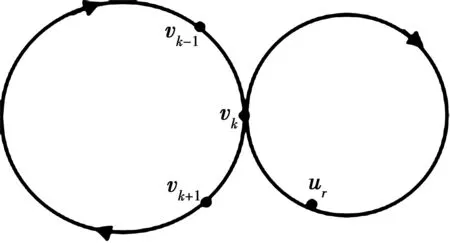
图3 没有S-路存在

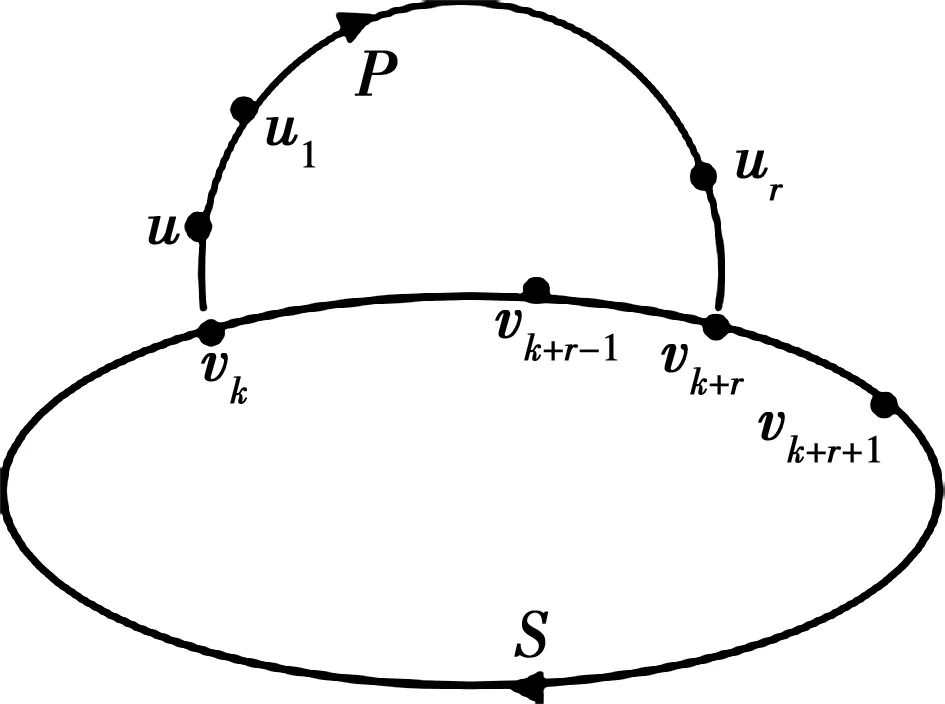
图4 存在S-路

情况2.如果R中有一个S-路P,设P=(vk,u,u1,…,ur,vk+r)，其中k+r对模n同余;P,vk,以及vk+r使得r是所有S-路中的最小值.

由S是R中长度最大的一个有向圈,得到{(vk+r-1,u),(vk+r-1,ur)}∩A(R)=Ø.如果(vk+r-1,u)∈A(R),那么S-(vk+r-1,vk+r)+{(vk+r-1,u),(u,u1),…,(ur,uk+r)}就与S是R中长度最大的有向圈的条件相违背;如果(vk+r-1,ur)∈A(R),那么S-(vk+r-1,vk+r)+{(vk+r-1,ur),(ur,vk+r)}同样与S是R中长度最大的有向圈的条件相违背.因此我们可以得到{(vk+r-1,u),(vk+r-1,ur)}∩A(R)=ø且r>1(见图4).

因为r是所有S-路中的最小值,所以(ur,vk+r-1)∉A(R).这就意味着R({vk+r-1,vk+r,vk+r+1,ur})是R的诱导子图也是图2中的一种存在情况.

我们受到不含图1和图2中禁止诱导子图的定向图是哈密尔顿的性质启发,进而考虑了在超欧拉有向图中,是否能找到不能含有哪些禁止诱导子图能够使得有向图满足超欧拉的性质的情形.首先如果有向图D是强连通的,则在D中一定存在S-路.

定理2设D是一个至少有3个点的强连通有向图,如果D不含图3中的诱导子图,则称D是超欧拉有向图.

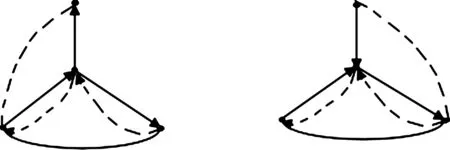
图5 0≤虚线的条数≤1;0≤实线的条数≤2

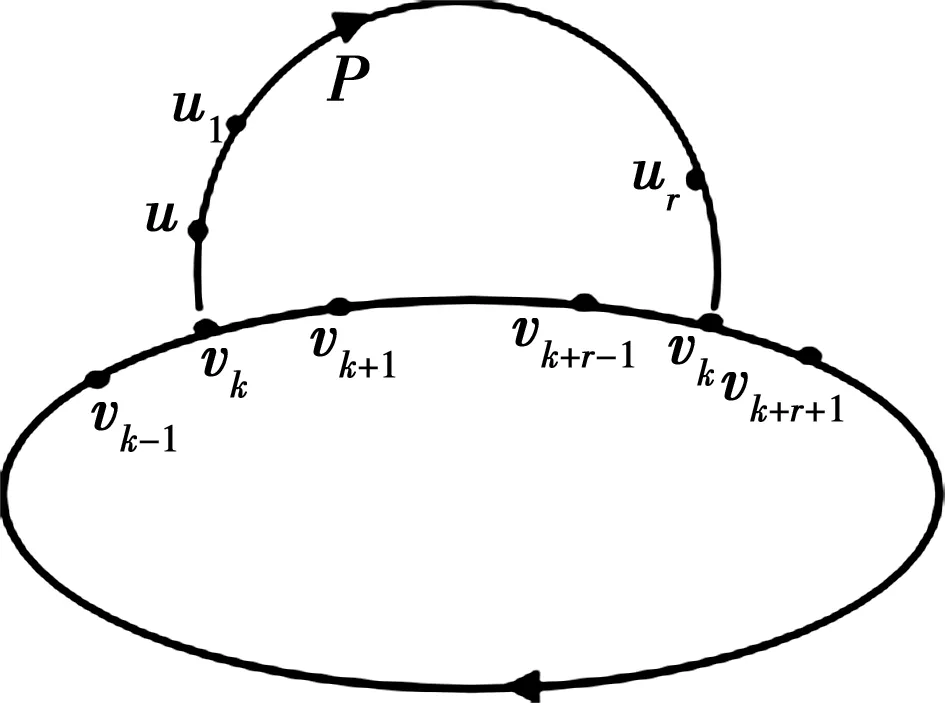
图6 存在S-路

其中未标方向的弧，其方向可任意

证: 设D是一个至少有3个点的强连通有向图,且不含图5中的诱导子图,但D是非超欧拉有向图.

令S=(v1,v2,…,vn,v1)是有向图D中点数最多的一个欧拉子有向图且弧数最多.因为D是强连通有向图但非超欧拉有向图,故D中存在一个S-路P;设P=(vk,u,u1,…,ur,uk+r),其中k+r对模n同余;P,vk以及vk+r使得r是所有S-路中的最小值.

由S是D中点数最多的欧拉子有向图,我们可以得到{(u,vk+1),(ur,vk+1)}∩A(D)=Ø,{(vk+r-1,u),(vk+r-1,ur)}∩A(D)=Ø.

如果(u,vk+1)∈A(D),那么S-(vk,vk+1)+{(vk,u),(u,vk+1)}就违背了S是D中点数最多的欧拉子有向图这一条件;如果(ur,vk+1)∈A(D),那么S-(vk,vk+1)+{(vk,u),(u,u1),…,(ur,vk+1)}同样也是违背了S是D中点数最多的欧拉子有向图这一条件.

综上所述,{(u,vk+1),(ur,vk+1)}∩A(D)=ø且r>1(见图6).另外,0≤|{(vk-1,u)(u,vk-1)}∩A(D)|≤1;如果{(vk-1,u),(u,vk-1)}⊆A(D),那么S+{(vk-1,u),(u,vk-1)}就违背了S是D中点数最多的欧拉子有向图这一条件.又因为r是所有S-路中的最小值,所以(vk+1,u)∉A(D).这就意味着D〈{vk-1,vk,vk+1,u}〉是D的诱导子图也是图3中的一种存在情况.

如果(vk+r-1,u)∈A(D),那么S-(vk+r-1,vk+r)+{(vk+r-1,u),(u,u1)，…,(ur,vk+r)}就与S是D中点数最多的欧拉子有向图的条件相违背;如果(vk+r-1,ur)∈A(D),那么S-(vk+r-1,vk+r)+{(vk+r-1,ur),(ur,vk+r)}同样与S是D中点数最多的欧拉子有向图的条件相违背.因此我们可以得到{(vk+r-1,u),(vk+r-1,ur)}∩A(D)=Ø.另外,0≤|{(vk+r+1,ur),(ur,vk+r+1)}∩A(D)|≤1;如果{(vk+r+1,ur),(ur,vk+r+1)}⊆A(D),那么S+{(vk+r+1,ur),(ur,vk+r+1)}就违背了S是D中点数最多的欧拉子有向图这一条件.又因为r是所有S-路中的最小值,所以(ur,vk+r-1)∉A(D).这就意味着D({vk+r-1,vk+r,vk+r+1,ur})是D的诱导子图也是图5中的一种存在情况.

[1]Bang-Jensen.J,Gutin G. Digraphs: Theory[M].Algorithms and Applications, SecondEdition, Springer, 2010.

[2]Boesch F T,Suffel C,Tindell R.The spanning subgraphs of eulerian graphs[J].Journal of Graph Theory, 1977(1):79-84.

[3]Pulleyblank W R.A note on graphs spanned by Eulerian graphs[J].Journal of GraphTheory, 1979(3):309-310.

[4]Catlin P A.Supereulerian graphs: a survey[J].Journal of Graph Theory,1992(16):177-196.

[5]Lai H J,Shao Y,Yan H.An update on supereulerian Graphs[J].World Scientificand Engineering Academy and Society Transactions on Mathematics, 2013,12(9):926-940.

[6]Alsatami K A,Zhang X D,Liu J,Lai H J.On a class of supereulerian digraphs[J].Applied Mathematics,2016(7):320-326.

[7]Bang-Jensen J,Maddaloni A.Sufficient conditions for a digraph to be supereulerian[J].Journal of Graph Theory,2015,79(1):8-20.

[8]Hong Y, Lai H G,Liu Q.Supereulerian digraphs[J].Discrete Mathematics, 2014,330:87-95.

[9]Faudree R,Flandrin E,Ryjacek Z.Claw-free graphs — A survey[J].Discrete Math.,1997,164:87-147.

[10]Kemnitz A,Greger B.A forbidden subdigraph condition implying an oriented graph to be hamiltonian[J].CiteSeer, 1970.