椭球罩作用下的水下爆炸冲击波反射聚焦模型*

郭 锐，刘 磊

(1.南京理工大学机械工程学院,江苏 南京 210094;2.埃因霍温理工大学机械工程系,荷兰 埃因霍温 5600MB)

由于能带来可观的定向性和压力增益，冲击波聚焦技术被广泛应用于医疗、探测和水声对抗中[1-2]，但相应的工程技术还不完善，对冲击波反射和聚焦机理的研究正日益受到重视[3-4]。

研究人员首先对波聚焦进行了大量实验和数值观察。Müller[5]通过实验研究了反射罩几何参数和材料特性对水下波反射聚焦的影响。陈景秋等[6]、韦春霞等[7]结合双特征法和CCW法模拟了球面反射罩条件下的水下聚焦过程，并指出实际焦点往往不与几何焦点重合，但雷开卓等[8]则通过多次实验结果观察到几何焦点也可能是实际焦点。Taieb等[9]利用带宽优化后的WENO格式模拟了冲击波聚焦过程，并对比实验结果指出了该方法对流动特性细节捕获的有效性，Oshita等[10]则利用高速摄影技术可视化水下聚焦细节，发现聚焦后的气泡破裂引起的压力可与焦区压力比肩。结合实验和数值模拟，张振福[11]进行了更细节性的研究，特别指出金属罩变形会引起实际焦点的轻微后移。

在理论研究方面，Coleman等[12]、Hamilto[13]分别引入一维频域和改进线性频域模型来模拟反射聚焦冲击波的传播过程。王鸿樟等[14]则基于线性声学理论，对空气背景下的内外聚焦声场进行建模分析，并指出焦平面位置的声压可近似为高斯分布。Cates等[15]进一步考虑了冲击波的非线性，将几何动力学应用于聚焦分析过程中，提出了反射壁面附近的三波点形成机理。Zhou等[16]则从等效源角度，将椭球罩等效为一个具有自适应球面波分布的聚焦源，据此研究了空气中的聚焦过程。对于水介质背景，Liu等[17]通过对反射模型的近似化，建立起刚性无损反射条件下的非线性聚焦模型，模拟结果表明理想情况下的动力学焦点出现在几何焦点之前。

综上所述相对于水下情形，当前模型多着眼于空气中的反射聚焦过程，且对于实际焦点的位置，现有结论间存在一些矛盾，故需进一步探究与解释。本文中提出水下冲击波(爆炸源)在椭球罩作用下的反射聚焦压力模型，并对比文献[11]的实验进行初步验证，此模型可在一定程度上解释现有矛盾。

1 聚焦模型

线性声理论表明从F1发出的波在经椭球罩作用后将到达F2，如图1[11]所示。一般而言声与光波符合该规律，但对于冲击波[6,18]，入射角不等于反射角，且反射波束将在到达轴线前发散。

建模假设如下：(1)忽略声源尺寸影响并考虑刚性反射罩；(2)忽略静水压力且并考虑常温环境；(3)内聚焦过程中，各反射波束存在时间差，能够沿着直线独立传播和汇聚；(4)反射波前和边缘衍射波前均为球面；(5)忽略杂质和气泡引起的空化效应，且忽略1次压力波后续的脉动波。将整个过程分为自由传播，壁面反射，定向聚焦阶段，并逐一讨论。

1.1 自由传播

自由传播中只存在直达波。水下冲击波峰值压力和衰减常数(指数衰减形式)与传播距离的经验关系为[19]：

(1)

式中：pm为峰值压力，R为传播距离，Kp和κ为pm对R的相似常数，m为装药质量，r为装药半径，τ为衰减常数，Tp和γ为τ对R的相似常数。引入指数余弦形式描述压力随时间的波动衰减特征[20]：

φ(t)=exp[(t-t0)/τ′]cos[ω(t-t0)]

(2)

式中：t0为冲击波前的到达时间，τ′为采用指数余弦形式代替常规指数形式时的等效衰减常数，ω为压力脉动频率。将两式结合可快速计算自由传播阶段的压力场，及其他阶段的直达波压力场。

1.2 壁面反射

壁面反射为瞬时阶段，且不同来向波束的反射时刻不同。考虑规则反射并结合假设(1)，可写出水中的入射和反射冲击波关系[18]：

(3)

进一步考虑入射波的透射损失，得到的反射波后压力修正为：

(4)

式中：反射系数Z(大小在0～1之间)由材料特性决定。将椭球罩内壁几何离散化，利用式(3)～(4)可计算各入射波束的反射压力和角度，作为后续聚焦过程计算的初值。

1.3 定向聚焦

定向聚焦分为内、外聚焦，分别定义为所有入射波束均完成反射过程之前、后的阶段。在内聚焦中，各反射波束沿直线传播，类似于线性汇聚，故可独立考察各反射波束的传播过程；进入外聚焦过程后，各反射波束将共同移动，因此相互干涉，从而不再能够沿直线传播，并会在焦区的高压作用下发散开。定义几何焦点连线中点为原点，近似描绘反射聚焦过程的波前与波法线几何形状见图4。

在图4中所示：Cw为波前中心，Ew为反射罩边缘点，Uw为反射波法线上的点，Ow为波法线在Uw处的切线与轴线的交点；聚焦边界为反射与边缘衍射波接触面。压力分布的数值计算域可用各反射波束的波法线和波前几何形状确定。将反射罩内壁划分为N个单元后，考虑波前中心位置为参考点并结合假设(5)，可将反射元j对应的反射波前及聚焦边界外的衍射波前几何方程分别表示为：

(5)

式中：“| |”表示两点距离，(xw,yw)为波前上任意一点的坐标；(xo,yo)为Ow的坐标，(xe,ye)为Ew的坐标，(xu,yu)为Uw的坐标，(xc,yc)为Cw的坐标，h为人工边界(压力为零)对应的径向坐标；对于yu的确定，考虑各反射元有且只有一条对应的反射波法线，并在折转点位置引入一段圆弧来粗糙过渡，因此将单元j对应的反射波法线视作两段直线段和一段圆弧段的组合。

1.3.1内聚焦

若不考虑介质吸收效应，则相同冲击波的波前“1”和“2”间功率关系可写作：

(6)

式中：A、p、ρ、和c分别为波前面积、相应的介质压力、密度和声速。根据水的Tait方程，密度和声速关系可表示为[6]:

(7)

考虑B≫p，则式(7)可简化为[17]：

(8)

再将式(8)带入式(6)，并考虑冲击波功率吸收效应，可得完整的压力关系式：

μ1Λ*2=(μ2Λ*+μ3)(μ4Λ*+μ5)

(9)

式中：Λ*=Λ[R1/(R1+ΔR)]η,指数η可通过实验确定；Λ=p2/p1,μ1=A2/A1,μ2=p1/(Bn),μ3=1-μ2,μ4=p1(n+1)/(4Bn),μ5=1-μ4。将假设(3)与式(9)相结合，可得内聚焦过程中的压力分布。

1.3.2外聚焦

将各波前视作一个压力不均匀的整体，则相邻的整体波前间的功率关系可写作为：

(10)

其中对于p(xw,yw)的形式，假设能用一个显式函数充分近似：

(11)

在此假设下，波前压力分布将具有前向递推关系。至此完成了整个反射聚焦压力分布建模。

2 模型验证

基于文献[11]的实验条件，利用所建模型对聚焦过程进行模拟和验证。椭球反射罩的长半轴a为500 mm，短半轴b为250 mm，深度L为300 mm，材料为不锈钢，声阻抗为45.6×106kg/m2·s远大于水介质声阻抗1.48×106kg/m2·s，典型正反射系数0.92；液电声源放电间隙为2 mm，输出电压22.627 kV，电容1×10-6F；采用138A05压力传感器，各轴向传感器与声源距离依次为233、433、643、723、800、866和953 mm。

2.1 材料与介质参数

由于模型中使用爆炸源，因此需要首先按照能量等效理论对液电源进行等效TNT球形装药处理。相应地，等效TNT装药质量m=0.012 1 g，等效TNT装药体积V=7.43 mm3，等效TNT装药半径r=1.2 mm，爆热Q=4 227 J/kg，密度ρ=1 630 kg/m3。

进行反射聚焦模拟前，需要确定材料和介质参数Kp、κ、Tp、γ和η。首先利用直达波压力数据[11]来确定压力随爆距的相似系数Kp和κ，拟合结果如图5所示。

由图5可知，拟合值Kp=27.75 MPa、κ=1.17和R2=0.987 7。尽管拟合结果与经验值有出入，但是能较好地反映该实验真实情况，且不影响模型本身使用，再根据文献[18]可得Tp=0.084 ms，γ=-0.23。图6表明，与直达波相比，聚焦压力脉动周期随着传播距离的增加而明显增大。通过指数拟合可近似描述聚焦压力脉动周期Tf和传播距离R间的关系为：

Tf(R)=0.012 5e1.121RR/r>12

(12)

以初始波前中心压力为参考，利用最小二乘法可估计出参数为0.63。

2.2 波前压力分布函数

(13)

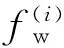
2.3 压力历史

对轴向特定位置的压力历史进行求解，并与文献[11]实验结果对比如图8所示。图中所示的曲线1～7所属轴向传感器距离声源依次为233、433、643、723、800、866和953 mm。可以看出7个位置所计算出的压力波形(忽略后续脉动波)与文献[11]中实验结果相似(文献[11]中的实验值为虚线所示，本文中所建模型得到的计算值为实线)，静水声速设为1 500 m/s。随着反射聚焦波的轴向传播，峰值压力先是增加，在经过动力学焦点后不断减小，拉伸波同样产生聚焦现象，并带来明显的局部负压，但是其变化较为平缓，且峰值相比于正压峰要出现得更早，约提前20 mm；计算所得波前到达时间稍小于测试值，可认为是初始声速设置偏差所引起的；计算所得聚焦正压的极大值小于实验结果约8%，且相应的动力学焦点(几何焦点前约50 mm处)比测量值提前约35 mm出现，究其原因：实际的反射罩在冲击波作用下将产生一定的压缩变形和背向位移(约数十微米[11])，使得反射角轻微减小，反射波的传播轨迹受到影响，因此“折转点”将向F2靠近(见图4)，使得动力学焦点向正轴向方向偏移，且相应的焦斑尺寸也会缩小，从而产生比理想情况更高的聚焦压力。可见该机制为动力学焦点在F2处及其后方出现提供了可能性。综上所述，所建模型能较好地描述各位置上的聚焦压力特性，尤其对于正压峰值，预测误差多在10%以下。

3 全场结果与讨论

为了细致地观察聚焦过程，给出压力分布随时间的变化关系如图9所示。图中可以看出经反射后，波前压力突然增加；在内聚焦中，各反射元对应的反射波束陆续汇聚到同一波前上，使得近轴的局部高压区不断扩展，但由于存在先后关系，故各波束间干涉不明显，从而压力随传播距离的衰减效应占据主导，使得整体波前的压力趋于减小，几乎没有聚焦效果；在外聚焦中的前半阶段，各反射波束均趋于向几何焦点附近移动，由于聚焦区域内较外侧的波束法线与轴线的夹角较大(锐角)，故其除了压缩前进方向上的介质外，还会对较内侧介质产生侧向压缩作用，因此越靠近轴线，介质受到的侧向压缩作用越强，压力增加得越快，换言之，能量趋于向近轴区集中，最终局部高压区的快速收缩将占据主导地位，使得聚焦压力快速增加，但相应的焦区阻抗也不断增大；当到达一极限位置时(动力学焦点附近，不一定重合)，较外侧的波束再也无法对较内侧介质产生侧向压缩作用，相反地，较内侧介质由于具有更高的压力，开始压缩较外侧介质，使得高压区再次不断扩展，能量开始向侧向扩散，相应的聚焦压力快速减小；整个波前的形状不断改变，特别是在动力学焦点附近时，中间部分几乎为平面，这是由于越靠近轴向，介质密度越大，冲击波传播速度越快；拉伸波也发生了明显的聚焦现象，并引起一道持续收缩的拖尾，可以认为是波后水介质存在惯性，难以立即跟上波前运动所引起的。

全场的聚焦压力峰值和增益分布云图分别如图10～11所示。从图中可以看出，由于椭球反射罩的聚焦作用，使得大部分爆炸能量集中于轴向方向，并产生出具有一定几何尺寸和较高的压力增益区(9.5～12.5 dB)，峰值增益约12.5 dB，高压力增益区的轴向跨度约500 mm(a的长度)，侧向跨度约50 mm(0.1a的长度)；从反射位置开始，压力峰值先减小，然后缓慢增加直至在动力学焦点附近达到极大值，之后再次缓慢减小。此外，应当注意波前压力分布近似函数(误差见图7)引起的，内/外聚焦压力场间的轻微不连续现象。综上所述，聚焦效应很好地削弱了波压力随距离的衰减作用，使得近轴方向上的冲击波能够在较长的距离内保持高压力进行传播。

4 结 论

建立水下爆炸冲击波经椭球罩作用下的非线性聚焦模型，并结合实验结果进行模型验证和全场压力变化模拟，主要结论如下：

(1)虽然存在一些粗糙的假设，但所建模型依然能在一定细节上反映聚焦机理，并对聚焦压力提供良好预测，尤其是正压峰值的预测误差多在10%以下，基本满足工程要求；

(2)椭球反射罩能有效地实现水下冲击波聚焦，产生一个具有和长半轴长相当跨度的狭长增益区(9.5～12.5 dB)，使得近轴方向冲击波随距离的衰减效应显著削弱，此外还伴随着拉伸波聚焦和持续拖尾现象，出现了局部负压区，相应峰值要早于正压峰值出现；

(3)理想情况下的动力学焦点将处于另一几何焦点之前，但实际中反射罩在冲击波作用下会发生些微变形和背向位移，使得动力学焦点重合于几何焦点，乃至其后方成为可能。

[1] CLURE S M, WEINBERGER T. Extracorporeal shock wave therapy: Clinical applications and regulation[J]. Clinical Techniques in Equine Practice, 2003,2(4):358-367.

[2] 李宁,雷开卓,黄建国,等.水下冲击波聚焦声场非线性建模与分析[J].系统仿真学报,2011,23(1):61-64.

LI Ning, LEI Kaizhuo, HUANG Jianguo, et al. Nonlinear modeling and analysis of underwater shock wave focusing sound field[J]. Journal of System Simulation, 2011,23(1):61-64.

[3] 陈景秋,韦春霞,邓艇,等.体外冲击波碎石技术的力学机理的研究[J].力学进展,2007,37(4):590-599.

CHEN Jingqiu, WEI Chunxia, DENG Ting, et al. Studies on mechanical mechanism about stone comminution and tissue trauma in extracorporeal shock wave lithotripsy[J]. Advances in Mechanics, 2007,37(4):590-599.

[4] RASSWEILER J J, KNOLL T, KÖHRMANN K U, et al. Shock wave technology and application: an update[J]. European. Urology, 2011,59(5):784-796.

[5] MÜLLER H M. Focusing of shock waves in water by different ellipsoidal reflectors[C]∥Proceedings of the 17th International Symposium on Shock Waves and Shock Tubes, Pennsylvania, USA, 1990:143-148.

[6] 陈景秋.激波聚焦问题的CCW数值解[J].重庆大学学报,1992,15(2):27-31.

CHEN Jingqiu. Numerical solutions of shock wave focusing with CCW method[J]. Journal of Chongqing University, 1992,15(2):27-31.

[7] 韦春霞,张永祥,张晓艳,等.球面压电式ESWL聚焦的实际焦点的数值分析[J].重庆大学学报,2009,32(1):21-26.

WEI Chunxia, ZHANG Yongxiang, ZHANG Xiaoyan, et al. Numerical analysis of the shpehrical surface piezoelectricity ceramics extracorporeal shock wave lithotripsy launch[J]. Journal of Chongqing University, 2009,32(1):21-26.

[8] 雷开卓,李宁,黄建国,等.椭球反射罩聚焦特性实验研究[J].西北工业大学学报,2010,28(2):102-106.

LEI Kaizhuo, LI Ning, HUANG Jianguo, et al. Experimental research on focusing characteristics of the concave ellipsoidal reflectors[J]. Journal of Northwestern Polytechnical University, 2010,28(2):102-106.

[9] TAIEB D, RIBERT G, HADJADJ A. Numerical simulations of shock focusing over concave surfaces[J]. AIAA Journal, 2010,48(8):1739-1747.

[10] OSHITA D, HAMID S, HOSSEINI R, et al. Time-resolved high-speed visualization and analysis of underwater shock wave focusing generated by a magnetic pulse compression unit[J]. IEEE Transactions on Plasma Science, 2012,40(10):2395-2400.

[11] 张振福.水下冲击波聚焦的数值模拟与实验研究[D].长沙:国防科技大学,2012.

ZHANG Zhenfu. Numerical and experimental investigations on underwater shock wave focusing[D]. Changsha: National University of Defense Technology, 2012.

[12] COLEMAN A J, CHOI M J, SAUNDERS J E. Theoretical predictions of the acoustic pressure generated by a shock wave lithotripter[J]. Ultrasound in Medicine & Biology, 1991,17(3):245-255.

[13] HAMlLTON M F. Transient axial solution for the reflection of a spherical wave from a concave ellipsoidal mirror[J]. Journal of the Acoustical Society of America, 1993,93(3):1256-1266.

[14] 王鸿樟,于洪斌,黄平.连续球面波在凹椭球面上反射的聚焦声场[J].上海交通大学学报,1996(1):65-69.

WANG Hongzhang, YU Hongbin, HUANG Ping. Focused sound field due to reflection of spherical continuous wave from concave ellipsoidal surface[J]. Journal of Shanghai Jiaotong University, 1996(1):65-69.

[15] CATES J E, STURTEVANT B. Shock wave focusing using geometrical shock dynamics[J]. Physics of Fluids, 1997,9(10):3058-3068.

[16] ZHOU Y, ZHONG P. The effect of reflector geometry on the acoustic field and bubble dynamics produced by an electrohydraulic shock wave lithotripter[J]. Journal of the Acoustical Society of America, 2006,119(6):3625-3636.

[17] LIU L, GUO R, CHEN L, et al. A prediction model for two-dimensional pressure distribution from underwater shock wave focusing by an ellipsoidal reflector[J]. Journal of the Acoustical Society of America, 2016,140(6):4506-4516.

[18] COURANT R, FRIEDRCHS R. Supersonic flow and shock waves[M]. New York: Interscience Publishers Inc., 1956:327-331.

[19] COLE R H. Underwater explosions[M]. Princeton: Princeton University Press, 1948:110-120.

[20] CHURCH C C. A theoretical study of cavitation generated by an extracorporeal shock wave lithotripter[J]. Journal of the Acoustical Society of America, 1989,86(1):218-227.