抑制风电爬坡事件的双蓄电池组参数优化配置

，(.国网安徽省电力公司调度通信中心，安徽 合肥 3006；.合肥工业大学电气与自动化工程学院, 安徽 合肥 30009)

0 引 言

大规模风电并网引起电网功率波动[1-2]，为了有效平抑波动，在并网系统中加入储能装置以减少弃风及弥补缺额。

风电功率持续波动，单一蓄电池组储能系统(battery energy storage system,BESS)[3-4]存在充放电频率过高和满充满放的问题。这里采用双BESS[5]配置，两组蓄电池采用同步或异步控制策略进行交替充放电，改善了平抑效果。采用同步控制[6]时，两组蓄电池始终分别处于充、放电状态，可以及时响应波动极端的情况，但BESS的容量无法充分利用，造成成本增加；采用异步控制时，蓄电池可同时处于充电或放电状态来充分利用BESS的容量，但蓄电池组都处于充电状态时无法响应风电缺额。

风电爬坡事件是一种短时间尺度下的大幅波动，往往发生在切入风速至额定风速段和切出风速段，对蓄电池充放电过程有很大的冲击。风-储系统弃风对电网无冲击，而缺额只能依靠电网中其他发电设备弥补。合理规划弃风和缺额，充分利用风能资源实现经济最大化。

文献[7]研究了风电爬坡率与储能结合的优化控制，采用最佳荷电状态的方式进行优化，但未考虑精确的风电爬坡模型。文献[8-9]分别提出风-储系统的联合调度模型和基于正态分布的容量估算法，但未考虑储能系统的经济效益。

上述文献中，未结合风电爬坡事件、BESS控制策略和弃风经济性研究。下面综合考虑BESS运行条件，蓄电池采用同步与异步控制策略，以蓄电池的装置费用和使用寿命以及弃风缺额惩罚费用为目标函数，以风电场和BESS安全运行为约束条件，同时以功率波动越限概率和幅值为评价指标，采用IPSO算法优化配置BESS的额定容量及功率，降低风电场功率波动对电网的冲击，降低系统成本。算例对比不同爬坡事件定义的适用性、同步与异步控制策略的优劣性，分析弃风因素的经济性。

1 风-储并网系统模型

风电场侧装设两组蓄电池，风-储并网系统结构如图1，并网的输出功率满足：

Psys(t)=Pwt(t)-ΔPloss(t)+PB(t)

(1)

式中：Psys(t)为t时刻并网点的输出功率；Pwt(t)为t时刻风电场的输出功率；△Ploss(t)为t时刻风电系统的损耗功率；PB(t)为t时刻BESS的总输出功率，PB(t)≥0时，蓄电池放电；当PB(t)<0时，蓄电池充电。PB1(t)、PB2(t)为BESS1、BESS2t时刻的输出功率。

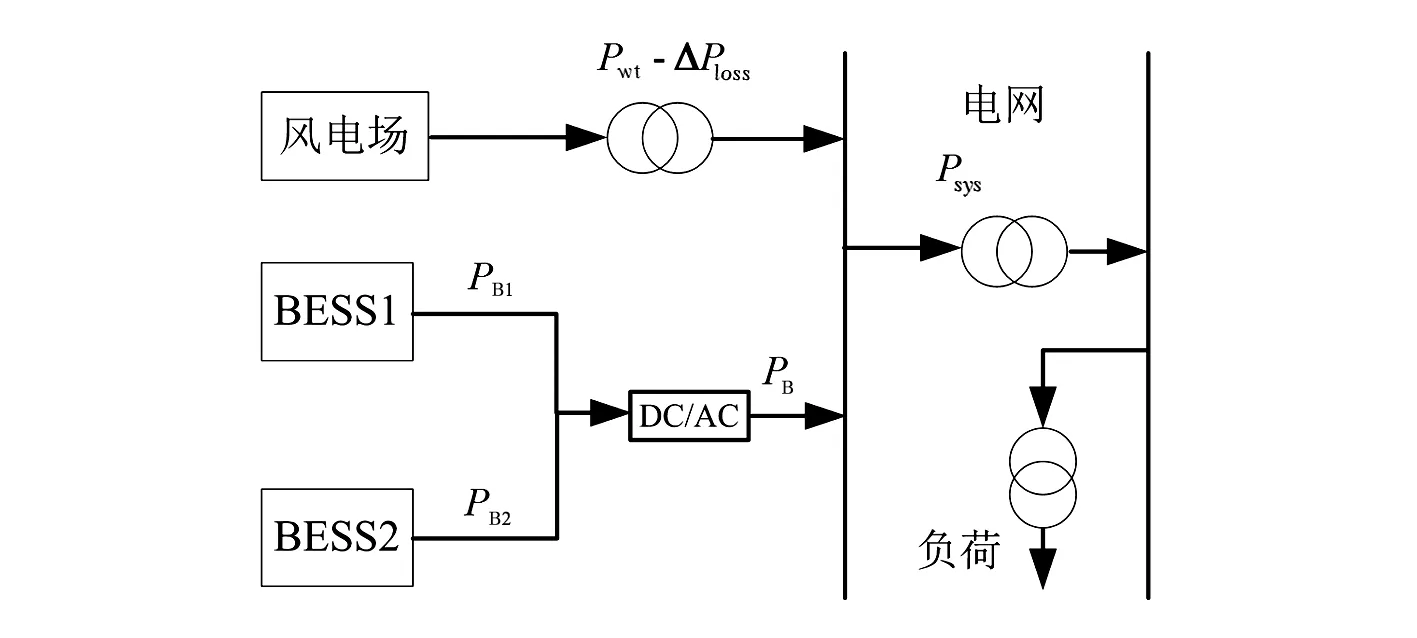
图1 风-储并网系统结构

BESS的平抑效果不要求输出为一条平稳的直线，只要满足国家风电并网标准[10-11]要求即可。

ΔPS(t)=|Psys(t)-Psys(t-Δt)|≤Pval

(2)

式中：ΔPS(t)为t时刻与相邻(t-Δt)时刻的功率差；Δt为采样时间间隔；Pval为并网功率波动限幅。

2 风电爬坡事件

当输出功率波动幅值大于波动限幅Pval时，认为发生爬坡事件，定义爬坡幅值：

1)t时刻和(t-Δt)时刻

ΔPwt(t)=Pwt(t)-Pwt(t-Δt)

(3)

2)时间段(t-Δt,t)内

ΔPwt(t)=max[Pwt(i)]-min[Pwt(i)]

(4)

3)引入t时刻的并网功率[12]

(5)

式中：i∈(t-Δt,t)；△Pwt(t)为爬坡幅值；△Pmax+(t)为t时刻与时间段(t-Δt,t)内的最小值之差；ΔPmax-(t)为t时刻与时间段(t-Δt,t)内的最大值之差。

式(3)、式(4)多用于静态优化控制计算，而式(5)为动态定义，可有效避免遗漏越限情况。所研究的BESS运行情况，爬坡事件数值特征越接近实际越理想。

3 双蓄电池组控制策略

t时刻风-储系统的输出功率波动幅值为

ΔPS(t)=ηwtΔPwt(t)-PB(t-Δt)+PB(t)

=ΔP(t)+PB(t)

(6)

式中：ηwt为风电系统效率(含损耗ΔPloss)；ΔP(t)为过渡变量。

BESS需要平抑的功率为ΔPB(t)。

(7)

式中,λ为安全裕度，保障电网安全。

蓄电池组储能过程满足：

(8)

式中：EB(t)为t时刻蓄电池组的剩余容量；ηch、ηdis为蓄电池组充、放电效率。

为了得到更好的平抑效果，对比同步与异步控制策略。

3.1 两组蓄电池处于不同状态

蓄电池组的最大充、放电功率为

(9)

式中:Pch(t)为蓄电池最大可充电功率；Pdis(t)为蓄电池最大可放电功率；PBmax为蓄电池额定功率(最大充放电爬坡率)；SOCmax为蓄电池最大荷电量；SOC(t)为蓄电池t时刻荷电状态；EBESS为蓄电池额定容量。

假设BESS1为充电状态，BESS2为放电状态。

1)充电时，BESS2的状态不变，PB2(t)=0；BESS1充电功率PB1ch(t)为

PB1ch(t)=-min{|ΔPB(t)|,|Pch(t)|}

(10)

2)放电时，BESS1的状态不变，PB1(t)=0；BESS2的放电功率PB2dis(t)为

PB2dis(t)=min{|ΔPB(t)|,|Pdis(t)|}

(11)

同步控制时，BESS1或BESS2任意一组达到满充或满放状态，下一刻BESS1和BESS2的状态都改变。

异步控制时，任意一组BESS达到满充或满放状态，下一时刻该组BESS改变状态，另一组保持不变。

3.2 两组蓄电池处于同一状态

只在异步控制时发生。

1)都处于充电状态：若|ΔPB(t)|可以被SOC(t-Δt)更接近SOCmax的蓄电池(假设为BESS1)全部吸收时，则根据式(10)计算；否则|△PB(t)|过大，两个蓄电池组同时工作，BESS1充电电功率为PB1(t)，BESS2的充电功率为

(12)

PB(t)=PB1(t)+PB2(t)

(13)

2)都处于放电状态：若|△PB(t)|可以被SOC(t-△t)更接近SOCmin的蓄电池(假设为BESS2)全部补足时，则根据式(11)计算；否则|△PB(t)|过大，两个蓄电池组同时工作，BESS2放电功率为PB2(t)，BESS1的放电功率为

(14)

3.3 弃风与缺额

弃风发生在蓄电池充电状态PB(t)<0:

(15)

缺额发生在蓄电池放电状态PB(t)>0:

(16)

系统并网功率重新定义为

ΔPS(t)=ηwtΔPwt(t)+ΔPB(t)-ΔPcur(t)

=ΔP(t)+PB(t)-Pcur(t)

(17)

式中,ΔPwt(t)、ΔPB(t)、ΔPcur(t)分别为t时刻与(t-Δt)时刻的风电、蓄电池和弃风功率差。

4 优化模型

4.1 目标函数

1)储能系统装置费用Fequip

Fequip=wEEBESS+wpPBmax

(18)

式中：wE为BESS的单位容量费用；wP为BESS的单位功率费用。

2)蓄电池寿命费用Fcount

蓄电池的充放电次数有限，完整交替充放电记一次充放电次数[13]。

(19)

式中：nch、ndis分别为充、放电次数；ntotal为寿命周期；Minv为蓄电池投资成本。

3)弃风缺额惩罚费用Fpunish

(20)

式中,wcur、wlack分别为单位弃风和缺额费用。

4)总使用支出费用Fcost

(21)

式中，w1、w2为各目标函数所占的比例。

4.2 约束条件

蓄电池的充放电功率需满足：

-PBmax≤PB(t)≤PBmax

(22)

为了避免过充过放，蓄电池组受到其荷电状态的限制。

SOC(t)=EB(t)/EBESS

(23)

SOCmin≤SOC(t)≤SOCmax

(24)

4.3 评价指标

功率波动越限概率和幅值越小，平抑波动的效果越好，控制策略越有效。

1)波动越限次数U

(25)

(26)

式中,S为二进制数，取0或1。

2)波动越限概率ΔU

(27)

式中，T为总时间。

3)波动越限幅值之和ΔW

(28)

4.4 改进粒子群优化算法(IPSO)

为避免PSO陷入局部最优，引入惯性权重wk，较大的wk有利于提高收敛速度，较小的wk有利于提高收敛精度[14]。

(29)

式中：Dt为当前粒子的迭代次数；Dtmax为算法开始设置的最大迭代次数；wmax、wmin为设置的最大和最小惯性权重。

随着迭代次数增加，希望粒子的搜索能力由局部寻优转为全局寻优，因此，加速常数c1逐渐减小，c2逐渐增大[15]。

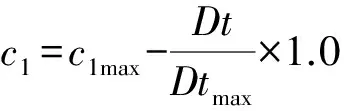
(30)

式中，c1max、c2min分别为最大和最小加速常数。

因此，粒子群速度和位置公式为

vDt+1=wkvDt+c1r1(pbest-pDt)+

c2r2(gbest-pDt)

(31)

pDt+1=pDt+vDt+1

(32)

式中：r1、r2为随机数；pbest为单个粒子最优位置；gbest为全局粒子最优位置；pDt为粒子第Dt次迭代时的位置。

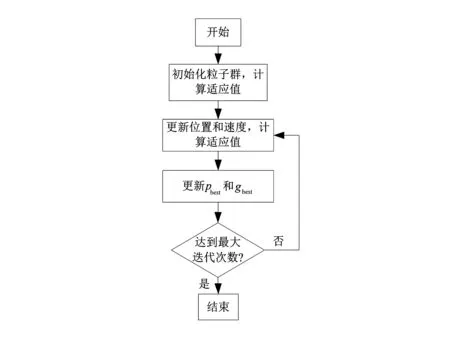
图2 IPSO算法流程

5 算例分析

算例中的风电场额定功率为50 MW，选取该风电场某典型日的风电功率实测数据，采样周期为1 min。风电功率10 min内输出的波动不超过额定功率的10%，安全裕度取0.9。表1给出BESS的装置参数和经济系数。

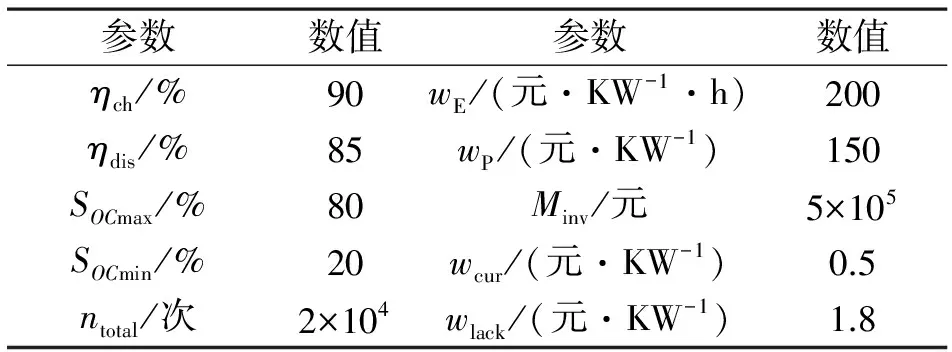
表1 BESS装置参数和经济系数

5.1 爬坡事件定义对比

分析不同定义下的风电爬坡事件。

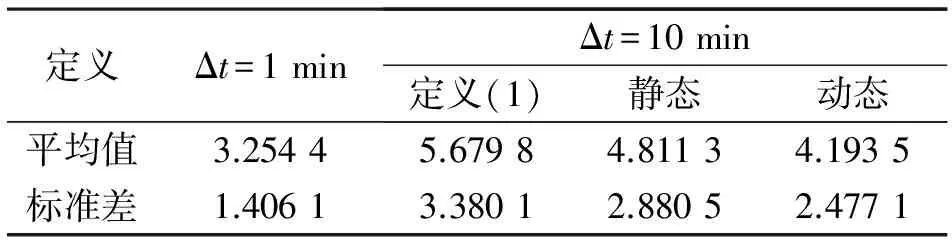
表2 风电爬坡事件数据特征

由表2可以看出，对比短时间的波动情况，可知动态定义下的数据平均值和标准差更能反映风功率的变化。

由图3可以看出，动态定义能采集到更完整的波动情况，因此选择动态定义进行研究更为合理。

蓄电池的充放电功率不仅受自身额定容量和功率的约束，而且受到并网条件的约束。因此，配置合适的蓄电池参数时需综合考虑。

5.2 对比异步、同步控制策略

选取两组额定容量均为10 MWh、额定功率均为5 MW的蓄电池，对比同步和异步控制策略的优劣性，见表3、表4。

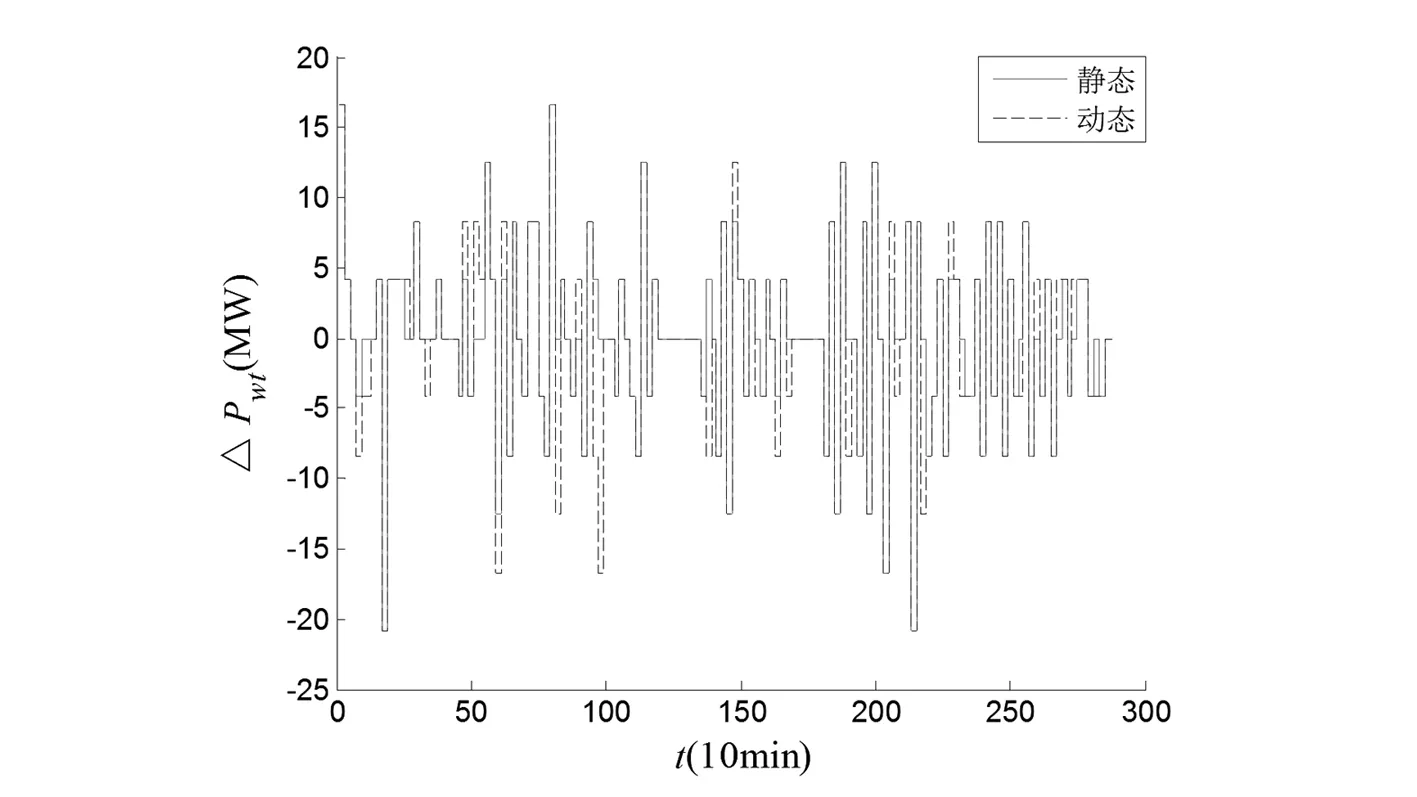
图3 不同风电爬坡事件对比

表3 BESS平抑前的指标

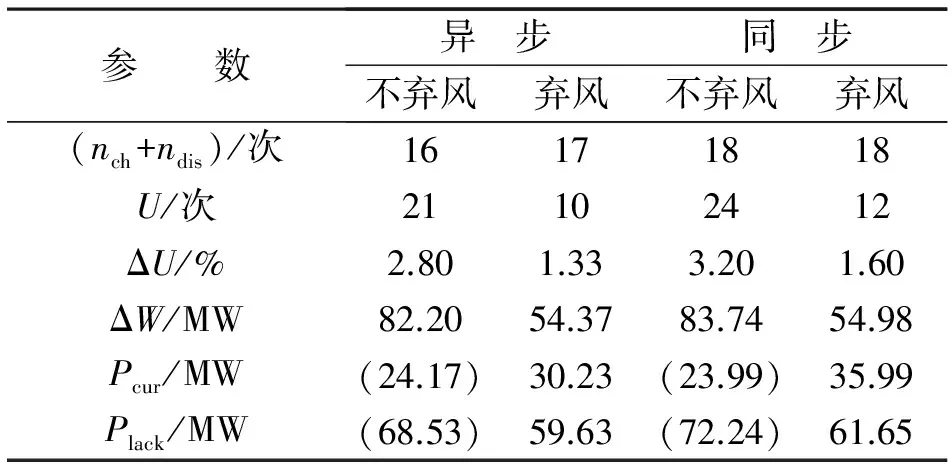
表4 异步与同步配置对比

由表3、表4可以看出，加入BESS后，波动越限概率和越限幅值大幅下降。舍弃多余的风电功率，明显地改善了平抑效果。对比两种控制策略下的指标可知，异步控制策略的波动越限概率及幅值都优于同步控制策略的。由分析可知，不同的额定容量和功率的BESS，容量和功率越大，输出波动越小，平抑效果越好，但会增加额外的系统装置费用。弃风和缺额总量与系统的额定功率及容量有关，综合考虑装置费用等因素，进行优化计算。

5.3 IPSO优化

IPSO中的各项参数：wmax=0.9，wmin=0.4，c1max=1.1，c2min=0.8。配置优化对比见表5，效果对比如图4所示。

由表5可以看出，异步控制策略的BESS额定容量及额定功率要求相差不多，且其平抑效果更好，因此计及越限及弃风缺额惩罚费用，其总体费用比同步控制的小。

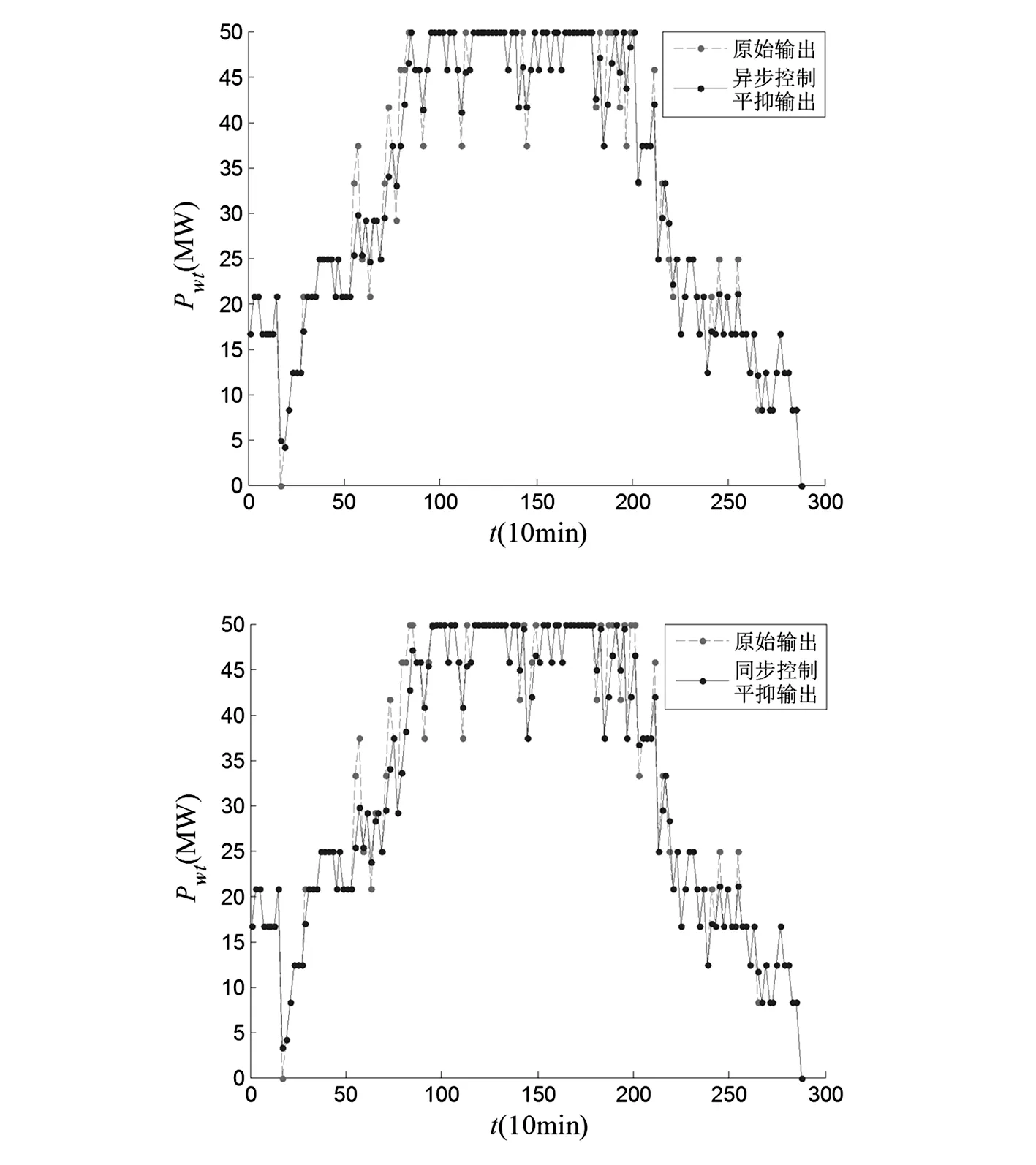
图4 同步与异步控制的平抑效果对比

由图4可以看出，在波动幅度较大时，异步控制更能充分利用蓄电池容量，最大限度利用风能，在不越限的情况下达到经济最优化。

6 结 语

前面提出了一种基于抑制风电爬坡事件的优化配置双蓄电池储能并网系统参数的方法。首先分析了风电爬坡事件的不同定义的适用性，动态定义的风电爬坡事件更能体现实测数据的特征。详细介绍了同步和异步控制策略，分析了两种控制策略的优劣性，可知异步控制策略能有效地利用蓄电池容量，且平抑波动的效果更好，经济性高。最后利用改进粒子群算法优化配置蓄电池组的参数。

[1] 汪海蛟, 江全元. 应用于平抑风电功率波动的储能系统控制与配置综述[J]. 电力系统自动化, 2014, 38(19): 126-135.

[2] 黎静华, 左俊军, 汪赛. 大规模风电并网电力系统运行风险评估与分析[J]. 电网技术, 2016, 40(11): 3503-3510.

[3] 邵丽华, 章竹耀, 张春龙, 等. 储能电池荷电状态与平抑风电出力波动协调运行策略[J]. 电力建设, 2017，38(1): 84-88.

[4] 娄素华, 吴耀武, 崔艳昭,等. 电池储能平抑短期风电功率波动运行策略[J]. 电力系统自动化, 2014, 38(2): 17-22.

[5] Cong-Long Nguyen, Hong-Hee Lee. A Novel Dual-battery Energy Storage System for Wind Power Applications[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10)：6136-6147.

[6] 章竹耀, 郭晓丽, 张新松，等. 储能电池平抑风功率波动策略[J]. 电力系统保护与控制, 2017, 45(3): 62-68.

[7] 何川, 刘天琪, 胡晓通, 等. 基于超短期风电预测和混合储能的风电爬坡优化控制[J]. 电网技术, 2017, 41(3): 782-790.

[8] 吴雄, 王秀丽, 李骏,等. 风电储能混合系统的联合调度模型及求解[J]. 中国电机工程学报, 2013, 33(13): 10-17.

[9] 程世军. 风电场储能系统的优化配置及运行研究[D]. 北京：华北电力大学, 2014.

[10] 侯婷婷.含大规模风电的电力系统储能电源优化配置研究[D]. 武汉: 华中科技大学, 2014.

[11] 谢应昭, 卢继平, 翁宗林, 等. 改善风电输出功率特性的复合储能系统优化配置[J]. 电网技术, 2016, 40(7): 2052-2058.

[12] 王颖, 张凯锋, 付嘉渝, 等. 抑制风电爬坡率的风储联合优化控制方法[J]. 电力系统自动化, 2013, 37(13): 17-23.

[13] Zhang X, Yuan Y, Hua L, et al. On Generation Schedule Tracking of Wind Farms with Battery Energy Storage Systems[J]. IEEE Transactions on Sustainable Energy, 2016, 8(1):341-353.

[14] 杨珺, 张建成, 黄磊磊,等. 基于改进粒子群算法的独立光伏发电系统储能容量优化配置研究[J]. 华东电力, 2012，40(8):1370-1374.

[15] Wang Yi, Jiang Hanhong, Xing Penxiang. Improved PSO-based energy management of Stand-alone Micro-grid under Two-time Scale[C]// IEEE International Conference on Mechatronics and Automation, 2016: 2128-2133.