基于重要节点的复杂产品设计变更控制

单炳冉，陶凤鸣

重庆大学现代管理与企业发展研究中心，重庆400044

基于重要节点的复杂产品设计变更控制

单炳冉，陶凤鸣

重庆大学现代管理与企业发展研究中心，重庆400044

CNKI网络出版：2017-04-01,http://kns.cnki.net/kcms/detail/11.2127.TP.20170401.0859.038.html

1 引言

随着全球经济增速放缓，美国、德国政府分别制定了“先进制造业国家战略计划”和“高技术战略2020”的国家发展战略，我国政府在此基础上结合自身经济特征，也提出了“制造业2025”发展战略。在“先进制造业国家战略计划”、“工业4.0制造”以及“制造业2025”中均提到：影响制造业水平的关键是制造业的设计能力[1-3]。

在制造业产品中，绝大部分是复杂产品（Complex Product，CP）。而在产品定制的需求多样化时代，复杂产品设计过程不可避免地面临设计变更这一根本性问题。设计变更是企业产品为满足客户的新需求谋求创新的源动力[4]。但在复杂产品设计过程中，因零部件间的关联关系，产品局部零件的变更会导致其他零件的更改，而与此对应的设计任务同样会因此变更引起连锁反应，加之任务之间复杂的关联关系，变更的影响可能传播至更远，甚至会发生雪崩式传播，最终使得复杂产品设计更加困难。如果控制不当，可能会导致设计任务拖期、成本增加，甚至降低产品设计质量[5]。目前，工业界和学术界大都基于复杂产品开发（Complex Product Development，CPD）网络中的重要节点来实施对复杂产品设计变更的控制[6]。因此，如何有效识别重要节点，给出相应的控制措施，对于控制复杂产品设计变更，防止发生雪崩传播[7]、最小化市场响应时间及开发成本等具有很高的实用价值。

传统评价节点重要性的主要方法是用度、介数以及紧密度中心性来衡量。宫中伟[8]等人利用图论等方法，通过对单个节点的向心指数C、密集指数S、连通指数E、中介指数M，4个重要性指标进行静态性分析，提出了识别Hub节点的算法，为设计变更提供了指导性建议。只考虑了节点在CPD网络中的局部属性，并未考虑节点在网络的全局属性与位置属性，并且识别Hub节点时的算法较复杂，计算量大。郭于明[9]等人对CPD网络进行了很大程度抽象，建立了小世界网络模型，结合变更传播强度，采用蚁群算法求解了变更传播路径。剔除了如设计节点状态及其节点之间的动态关联性等影响变更传播其他很多因素，而且只考虑了节点在CPD网络的全局属性，并未关注节点在CPD网络的局部属性与位置属性，未能实现对现实CPD网络的精确反映。

学术界普遍认为基于网络的全局和局部两大属性，能够很精确地识别网络中的重要节点，直到Kitsak[10]等人系统论证了节点的重要性是由网络中节点的位置决定的，认为传统的介数最大或节点度最大的Hub节点并非网络传播动力学中最重要的节点，而是具有最大K-核值的节点，并给出了K-核分解法的详细衡量方法。但无法有效区分同一K-核包含两个以上多个节点的重要程度；Bae[11]等人为了有效区分同一K-核两个以上的多个节点的重要程度，提出基于邻居核数的节点重要性排序算法，用邻居核数（Neighborhood Coreness）来识别它们的重要程度，并将所有邻居节点的K-核值之和定义为邻居核数，但是没有指出如何确定邻居节点的范围；温凯[12]等人以节点对网络的作用为导向，提出基于距离的影响力网络节点重要性评估法，指出一个节点到达网络中其他节点的距离越短，该节点的影响力范围增长速度越快，重要程度越强，反之则越弱。

综上所述，本文根据前人在复杂产品设计变更中重要节点识别研究中的不足，结合节点在CPD网络中的全局、局部、位置三重属性及对CPD网络进行加权，提出基于特征路径以内邻居核数的节点重要性排序算法，从而有效识别出CPD网络中的重要节点。该算法是一个考虑因素全面且更加科学、合理、简单、高效的节点重要性排序算法，具有很强的实用性。并在此基础上提出对重要节点的控制策略，为企业分析、控制复杂产品设计变更提供有效支持。

2 重要节点对设计变更的影响

类似于马太效应，客户总是花费更多的精力关注那些更重要的零部件上。所以，在产品设计过程中，针对这些关键零部件的需求变更概率相对更高[13]。

由于复杂产品设计过程中设计任务复杂交错的联系，把复杂产品的设计任务拓扑成CPD网络模型来研究。在CPD网络中有这样一些重要性巨大的关键节点，它们成为CPD网络的中心，统治着整个网络[14]。它们的节点度（与某节点相连接的其他节点的数目）极高，对应的传播路径多，扩散范围大，控制着CPD网络中的信息流动，很大程度上控制着变更的走向及传播的影响范围，其影响主要体现在下面三个方面：

（1）当设计变更传播经过一些重要节点时，有些重要节点会相应地吸收经过它们的设计变更，使变更传播的影响范围得到了有效的限制，从而减少了变更的时间及变更的成本；而另一些连接有大量边的重要节点，不仅会扩大设计变更的传播范围，同时也使得对设计变更的控制变得相对复杂。

（2）一些重要节点如果吸收了某些设计变更，并且传递给其他节点，有可能会引起这些节点在设计、工艺等方面的冲突。

（3）重要节点之间的相互影响及冲突是引起复杂产品设计变更的雪崩式传播的根本原因。

3 复杂产品设计网络

3.1 设计结构矩阵

在复杂产品的设计过程中，各个任务之间存在着大量相互影响的复杂关系，表现为任务之间的信息交互，这种信息交互可以通过DSM一一映射[15]。DonaldSteward在1981年引入设计结构矩阵（Design Structure Matrix，DSM），它能表示一对系统元素间的关系存在与否，与图形表示相比，它对整个系统元素提供整体的紧凑描绘，并为各项活动的信息需求、活动的顺序决策及活动迭代的控制提供有效的使用方法。

设计结构矩阵是一个二元的方阵（矩阵中的元素仅为0或1），若产品由n个零件ai()i=1,2,…,n组成，将各零件间的关联关系映射为矩阵，矩阵的行和列与产品零件相对应，零件均以相同的顺序放在矩阵的最左边和最上边，这样就构成一个n×n阶矩阵，目的是有利于对复杂产品进行可视化分析。如果元素ai和元素aj之间存在联系，则矩阵中的aij（i行j列）元素用数字1表示，表示零件ai的变更会引起零件aj的变更；否则空格或用数字0表示。其中主对角线元素标志着零件本身。

如表1，是一个简单的DSM，包含4个任务。容易发现，若a3发生变更，则直接被影响的任务有a1、a2和a4；a1发生变更，直接被影响的任务是a3、a4，间接被影响的任务是a2（a2是由a3影响直接影响的a2）。

3.2 构建加权CPD网络模型

把复杂产品结构拓扑成一个复杂网络，产品的每个零部件即为网络节点，零件之间的关联关系为网络边。由于零件之间的关联关系紧密性存在差异，相应每条网络边的权值也不尽相同，零件之间的关联关系越紧密说明网络边的权重越大[13]，可见复杂产品结构网络是一个加权CPD网络。

由于加权CPD网络通常用来对现实中具有层次结构、复杂内部关联的对象进行抽象建模。并且在设计变更的研究中，图论方法由于其表达的优良性质而被广泛应用[14]。用图G=()V,E,W来表示CPD网络，假设网络有N个节点，则V={v1,v2,…,vn}表示节点的集合，E={e1,e2,…,en}表示网络中节点之间边的集合，W=(w1,w2,…,wn)表示边权重集合。

对于加权CPD网络，边权(wij)可表示网络中节点间的关联程度，权值越大，两节点之间的距离越小，关系越亲密。由关联重要度优先原则，当某一零件配置参数发生变更时，与变更零件关联程度越高的零件受到的影响程度越大，越容易发生变更，且对节点边eij，有[16]：

其中，ki表示节点vi的节点度。

由根据公式（2），计算表1中各节点的节点度，并绘制表2。

表1 设计结构矩阵

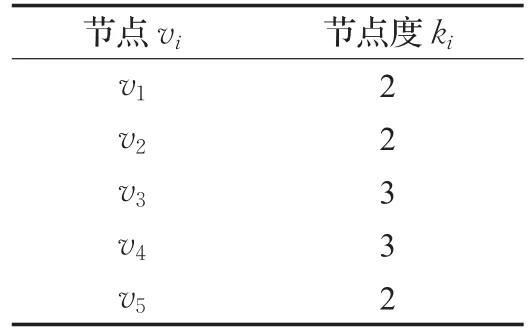
表2 节点vi的节点度ki

根据公式（1）算出每条边的权重，映射的加权CPD网络，如图1所示。

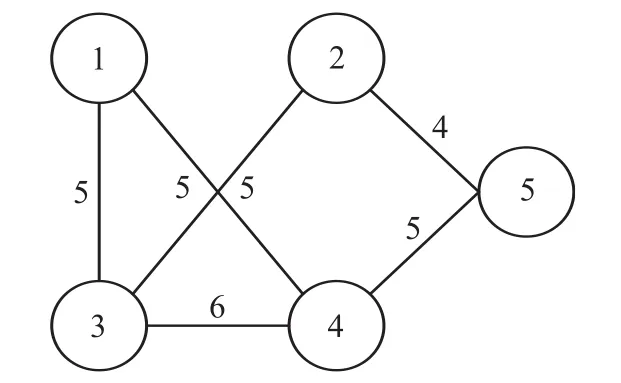
图1 加权CPD网络模型

4 节点重要性识别及控制

4.1 网络特征路径

特征路径长度是指网络中所有节点对之间的特征最短距离，是衡量复杂网络的一个极为重要的特征数量值，是衡量网络拓扑结构健壮的三个重要指标之一，是网络的紧凑性和相互通信的效率与性能。特征路径长度越小则说明网络越集中紧凑，相互通信的效率也越大[17]。

研究发现，如果一个网络具有较短的路径长度，那么对设计变更的传播有着很大的促进作用，对于加权CPD网络也是如此。一般的，最短路径是研究复杂网络的一个重要参数，长度代表着变更传播的深度，所以在传播强度相同的情况下，其传播速度和影响范围大大高于非最短路径。

由加权网络的意义可知：本文加权CPD网络的边权属于相似权。由于距离是权重的某种函数，两节点间权重越大，说明两点之间距离越短。定义每条边的长度为[13]：

用Dijkstra算法求出任意两个节点之间的最短路径dij。

Bae[11]等人认为节点的重要性受其邻居节点的影响；温凯[12]等人指出一个节点到达网络中其他节点的距离越短，该节点的影响力范围增长速度越快，它的重要程度越强，反之则越弱。为了使邻居节点更全面地参与对某节点重要性的衡量，在基于前人研究的基础上，本文运用网络特征路径L这一概念，以确保节点全局信息的准确性，这样节点重要性的衡量依据也就越全面。网络的平均直径L的公式如下：

其中，dij表示节点vi和vj之间的最短路径；N表示CPD网络中节点总数。

由公式（4）可知，最短距离会影响特征路径的大小，继而影响K-核分解之后的邻居核数值。在特征路径长度相同的情况下，最短路径越小，节点的邻居节点越多，邻居核数值也就越大，重要性也越强，反之越小。

4.2 K-核分解方法

Kitsak[10]等人系统论证了网络传播动力学中重要的节点，即K-核值越大，节点越重要，并给出K-核分解法的详细衡量方法。

K-核分解的方法[18]：CPD网络中含有大量节点，从节点度的中心性来看，节点度最小（度为1）的节点是设计变更传播过程中最不重要的节点，在设计变更传播中扮演只接收变更信息而不传送变更信息的角色，将这些节点度为1的节点删除并断开与其他节点的连边。如果删除那些节点度为1的节点之后，新形成的CPD网络中还有节点度为1的节点，则继续将新形成的节点度为1的节点删除并断开与其他节点的连边，直到新形成的CPD网络中所剩余的节点的度都大于1，则所有被删除的节点都属于1-核；接下来，删除节点度为2的所有节点并断开与其他节点的连边，直到新形成的CPD网络中所剩余的节点的度都大于2，则在新一轮中删除的节点都属于2-核；以此类推，直到最后一轮CPD网络中所剩余的节点度都为K时，则这些都是属于K-核的节点。

4.3 节点重要性的衡量指标

Bae[11]等人用邻居核数（Neighborhood Coreness）有效区分同一K-核两个以上的多个节点的重要程度，指出节点邻居核数的大小受节点的邻居节点的影响，离节点越远的节点对影响越小，甚至可以忽略不计，反之影响越大。

本文提出的基于特征路径以内邻居核数的节点重要性排序算法不仅能有效区分同一K-核包含上的多个节点的重要程度，还能兼顾节点的全局、局部、位置三重属性来识别CPD网络中的重要节点。其中节点vi重要性的衡量指标是基于特征路径以内的邻居核数（Neighborhood Coreness）值，值越大表示节点越重要。NC()viL′表示距离节点vi在特征路径以内(0≤L′≤L)的所有邻居节点的K-核数之和，定义如下：

定义1邻居核数公式：

其中，L′指距离节点vi的距离；N()vi表示节点vi的邻居节点集合；表示节点vi的邻居节点vj的K-核值。

定义2当L′=0时，有NC()vi0表示节点vi自身的K-核值。

定义3当0≺L″≤L时，有

定义4节点重要性的衡量指标：

根据公式（5）、（6）算出每个节点的邻居核数值，然后依次由大到小排序，就可以识别出CPD网络中所有节点的重要性程度。

4.4 节点重要性识别的排序算法步骤

根据定义1～4，可以给出CPD网络中节点重要性识别的排序算法，具体步骤如下：

步骤1根据公式（2），算出每个节点的度。

步骤2根据公式（1），算出每条边的权重。

步骤3根据公式（3），算出每条边的长度。

步骤4用Dijkstra算法求出任意两个节点之间的最短路径dij。

步骤5根据公式（4），算出CPD网络的特征路径L。

步骤6用K-核分解思想对CPD网络进行分解，计算出每个节点的K-核属性，即L′=0时，ND()vi0的值。

步骤7当L′＞L时，退出计算，否则继续执行。

步骤8根据公式（5）算出每个节点的衡量指标

最终，节点vi的衡量指标值越高，说明该节点在复杂产品设计变更传播中的重要程度越高。

4.5 基于重要节点的复杂产品设计变更控制策略

在复杂产品设计变更过程中，由于重要节点成为CPD网络的中心，被影响的概率非常大。因此为准确做出变更响应决策，有效降低变更影响，从重要节点出发，提出以下三个设计变更控制策略：

（1）扩大CPD网络中重要节点的设计参数阈值

在进行产品设计时，CPD网络中任务节点会有一定的设计参数阈值作为变更缓冲区。当发生某种变更时，对节点的影响程度超过自身变更缓冲区范围时，该变更就会被放大，反之变更就会被吸收。因此，在设计时，扩大CPD网络中重要节点设计参数阈值能有效减小变更影响范围。

（2）在满足产品市场交货期和保证产品性能的情况下，断开某些重要节点间的连接

一方面，对于一个设计变更，断开某些重要节点间的连接，能减少重要节点之间的相互影响，有效改变变更传播链，减小变更传播的范围；另一方面，如果出现多个设计变更，断开某些重要节点间的连接可以有效避免任务节点之间的反复设计冲突，有效防止设计变更发生雪崩传播。

（3）增加CPD网络中重要节点与其他节点之间的链路

在节点设计参数公差范围确定的情况下，通过重要节点与其他节点之间的链路，对设计变更进行“分流”，减少节点间的信息传递量，缓解重要节点的变更压力，在一定程度上减小变更传播的范围，有效防止设计变更发生雪崩传播。

5 工程实例验证

本文以某拥有32个零部件的摩托车发动机为例[8]，对所提的基于特征路径以内邻居核数排序算法进行验证。某摩托车发动机的DSM如图2所示。

由图2摩托车发动机结构的设计结构矩阵映射成的节点关联关系图，如图3所示。

根据公式（3）算出每个节点的节点度，如表3所示。

根据公式（2）算出每条边的权重，并绘制成的某摩托车发动机结构的加权CPD网络如图4所示。

根据图4发动机结构的加权CPD网络，先用公式（4）算出任意节点之间的最短路径lij，再用Dijkstra算法求出任意两个节点之间的最短路径dij并代入公式（5），求出加权CPD网络的特征路径L值为：

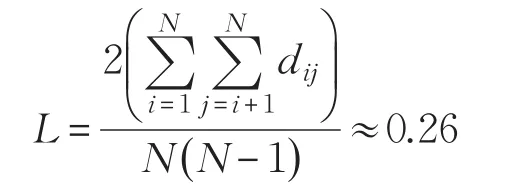
由分析可知0≤L′≤0.26。

用K-核分解方法对CPD网络进行分解，计算出每个节点的K-核属性，如表4所示。

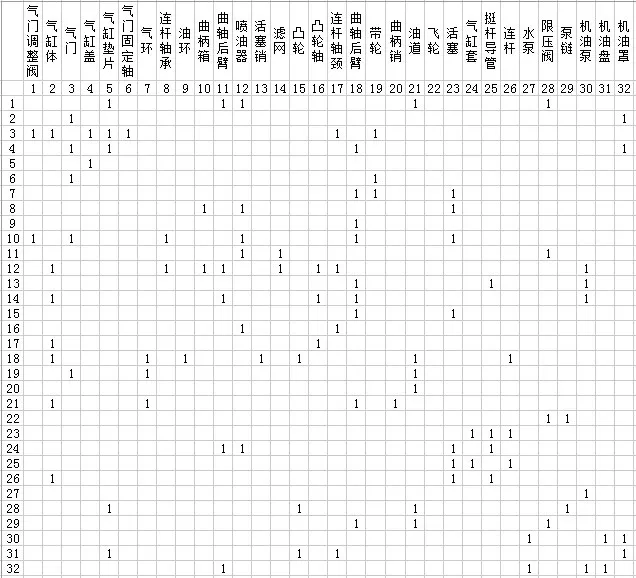
图2 某摩托车发动机结构的设计结构矩阵

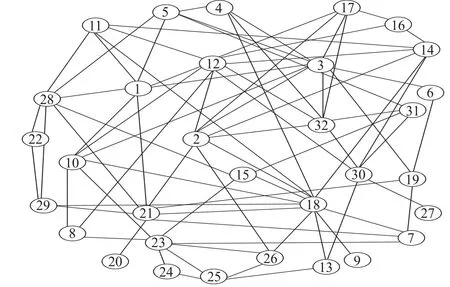
图3 某摩托车发动机结构的关联关系图

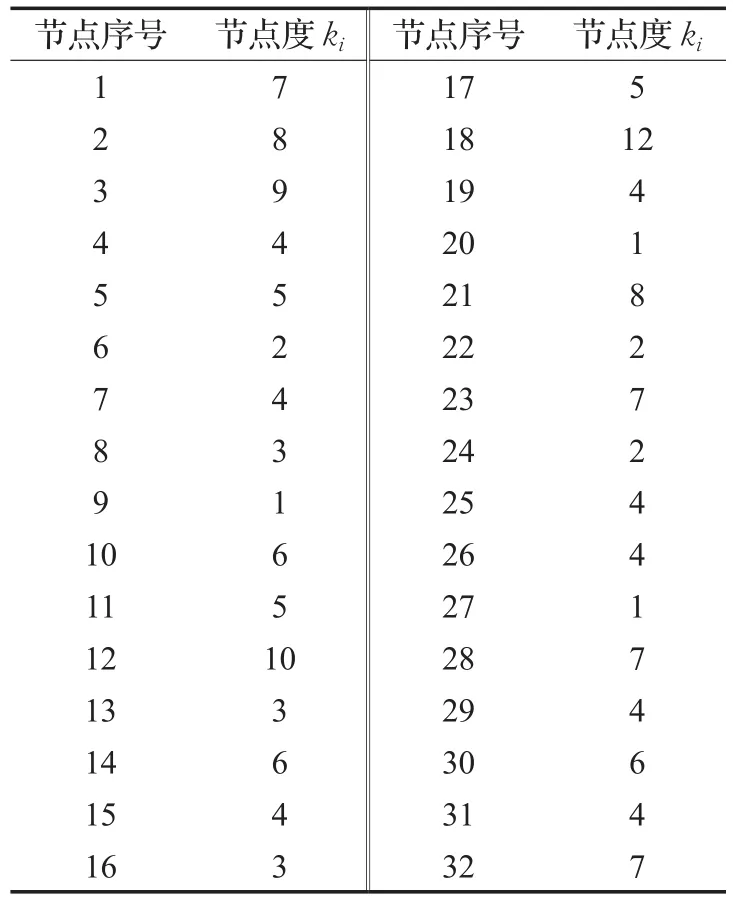
表3 每个节点的节点度ki

图4 某摩托车发动机结构的加权CPD网络图

根据公式（5）、（6）算出每个节点的邻居核数值，为了更具体地查看对摩托车发动机设计变更传播起重要作用的节点，本文给出节点重要性排序前7个节点和其对应值，并与文献[8]生成的结果进行比对，如表5所示。

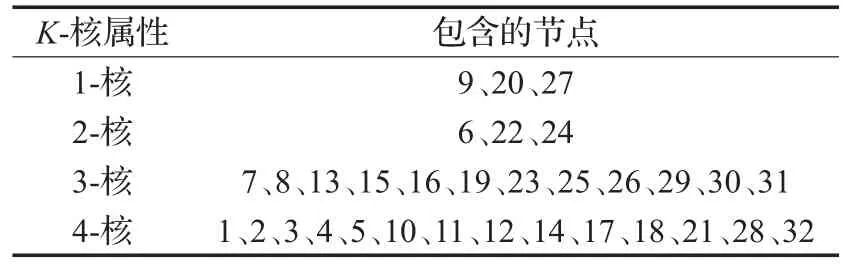
表4 每个节点的K-核属性

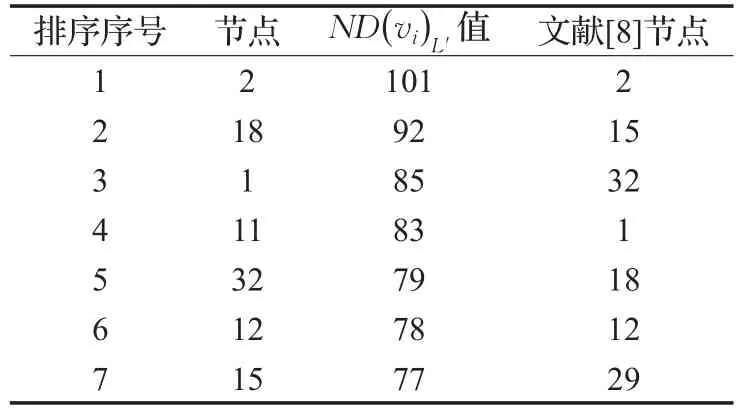
表5 序列中节点重要性排名前10的节点

实验结果与分析：由表5可知，用基于特征路径以内邻居核数的节点重要性排序算法得出的排序前7的重要节点是2、18、1、11、32、12、15。结果与文献[8]生成最重要的节点是相同的，都是节点2。生成的排序前7的重要节点集合是相同的，也即是需要控制的节点是相同的，但在排序上存在差异。这也客观地反映了在节点重要性排序问题上，因考虑因素及使用算法的不同，在生成相同重要节点集合的同时，得到的排序结果也有所不同。例如本文生成的排第2的节点18，在文献[8]中却排第5。从摩托车发动机结构的加权CPD网络图中可以看出，无论是从核属性，还是从节点度出发，节点18的重要性高于节点15的重要性。节点18的度比节点15大得多，也即是节点18连接了许多叶子节点，在设计发生变更时，节点18的传播能力要远强于节点15，而且渗透力更强。另一方面，文献[8]是从局部来看节点重要性，节点15在模块M1的传染能力很强，可以说是局部的重要节点。但从整个网络来看，节点18的重要性高于节点15。

实验的分析结果证明了基于特征路径以内邻居核数的节点重要性排序算法的科学性、准确性与有效性。相对于其他算法，该算法具有考虑影响因素更加全面、算法简单、易于理解、计算量小等优点。

6 结束语

目前，复杂产品设计变更控制是一个研究热点。本文从重要节点对复杂产品设计变更的影响出发，运用设计结构矩阵（DSM）及图论的相关知识，构建了加权CPD网络。在此基础上，结合节点的全局、局部和位置三重属性，提出基于特征路径以内邻居核数的节点重要性排序算法，并识别出CPD网络中的重要节点。该算法是一个考虑因素全面且更加科学、合理、简单、高效的节点重要性排序算法，具有很强的实用性，能准确地识别出复杂产品设计变更传播的“推波助澜”者，帮助设计者们尽快地找到网络中对设计变更信息流起传播作用的重要节点，并在此基础上提出基于重要节点的复杂产品设计变更控制策略，为企业分析、控制复杂产品设计变更提供有效支持。

[1] 王福君，沈颂东.美、日、韩三国装备制造业的比较及其启示[J].华中师范大学学报：人文社会科学版，2012，51（3）：38-46.

[2] Akgun A E，Keskin H，Byrne J C.Complex adaptive systems theory and firm product innovativeness[J].Journal of Engineeringand Technology Management，2014，31（1）：21-42.

[3] Fernandes J，Henriques E，Silva A，et al.A method for imprecision management in complex product development[J].Res Eng Des，2014，25（4）：309-324.

[4] 宫中伟，莫蓉，杨海成，等.基于矩阵的工程变更雪崩传播预测方法[J].计算机集成制造系统，2012，18（12）：2619-2627.

[5] 胡东方，郑亚飞，雷若楠.基于QFD和AIS的复杂产品定制设计[J].计算机集成制造系统，2016，22（9）：2053-2062.

[6] Jarratt T，Eckert C，Caldwell N，et al.Engineering change：An overview and perspective on the literature[J].Research in Engineering Design，2011，22（2）：103-124.

[7] Ouertani M Z.Supporting conflict management in collaborative design：An approach to assess engineering change impacts[J].Computers Industry，2008，59（9）：882-893.

[8] 宫中伟，莫蓉，杨海成，等.基于产品开发网络Hub节点的工程变更[J].计算机集成制造系统，2012，18（1）：40-46.

[9] 郭于明，王坚，凌卫青.基于小世界网络模型的复杂产品设计变更传播研究[J].制造业自动化，2011，33（1）：85-90.

[10] Kitsak M，Gallos L K，Havlin S，et al.Identification of influentialspreadersincomplexnetworks[J].Nature Physics，2010，6（11）：888-893.

[11] Bae J，Kim S.Identifying and ranking influential spreaders in complex networks by neighborhood coreness[J].Physical A：Statistical Mechanics and its Applications，2014，395（4）：549-559.

[12] 温凯，吴晔.一种基于距离的节点重要性评估方法[J].中国科技论文在线，2014.

[13] 于国栋.定制复杂产品设计中客户需求变更响应及其关键技术[D].重庆：重庆大学，2015.

[14] 张翼.复杂网络节点重要性评估及其应用研究[D].武汉：华中师范大学，2011.

[15] 闰喜强，李彦十，李文强，等.基于祸合强度和模糊设计结构矩阵的多学科解祸规划方法[J].计算机集成制造系统，2013，19（7）：1447-1455.

[16] Wei B，Liu J，Wei D，et al.Weighted k-shell decompositionforcomplexnetworksbasedonpotentialedge weights[J].Physica A：Statistical Mechanics and its Applications，2015，420：277-283.

[17] 谢斐，张昊，陈超.无标度网络中边权重对传播的影响[J].计算机应用研究，2013，30（1）：238-240.

[18] 任卓明，刘建国，邵凤，等.复杂网络中最小K-核节点的传播能力分析[J].物理学报，2013，62（10）：466-471.

SHAN Bingran,TAO Fengming.Design change control of complex products based on important nodes.Computer Engineering andApplications,2018,54（6）：222-227.

SHAN Bingran,TAO Fengming

Enterprise Development Research Center,Chongqing University,Chongqing 400044,China

To control complex products design change effectively,the influence of important nodes on complex product design changes is revealed in Complex Product Development（CPD）network.To identify important nodes,a weighted CPD network model is constructed,node importance ranking algorithm based on neighborhood coreness within the average path is proposed,in order to solve the non-comprehensive consideration of the process of ranking and the complexity of the algorithm process.The algorithm can consider the factors that affect the nodes importance comprehensively,more scientific,reasonable,simple and efficient to sort the nodes importance.On these basis,the control strategy of complex product design change from the important nodes is expounded.The effectiveness and rationality of the proposed method is verified through empirical study.

design change;weighted product development network;nodes importance;neighborhood coreness;control strategy

为了有效控制复杂产品设计变更，在复杂产品开发（Complex Product Development，CPD）网络中揭示了重要节点对复杂产品设计变更的影响。为了识别重要节点，构建出加权CPD网络模型，提出基于平均路径以内邻居核数的节点重要性排序算法，以解决排序过程中考虑因素的不全面性及算法过程的复杂性。该算法能够全面考虑影响节点重要性的因素，更加科学、合理、简单、高效地对节点重要性进行排序。并在此基础上阐述了从重要节点出发的复杂产品设计变更控制策略。通过实证研究，验证了所提方法的有效性和合理性。

设计变更；加权产品开发网络；节点重要性；邻居核数；控制策略

2016-10-08

2017-01-05

1002-8331（2018）06-0222-06

A

TP391

10.3778/j.issn.1002-8331.1610-0035

国家自然科学基金（No.71571023）；中央高校基本科研业务费资助（No.CDJZR13110072）。

单炳冉（1990—），男，硕士研究生，主要研究方向为复杂网络，复杂产品设计，E-mail：1549976201@qq.com；陶凤鸣（1976—），女，副教授，硕士生导师，主要研究方向为企业管理，供应链管理。