基于区域分解的并行动态LOD构建算法

魏子衿，肖丽

1.中国工程物理研究院研究生部，北京100088

2.北京应用物理与计算数学研究所，北京100094

3.中国工程物理研究院高性能数值模拟软件中心，北京100088

基于区域分解的并行动态LOD构建算法

魏子衿1，2，3，肖丽2，3

1.中国工程物理研究院研究生部，北京100088

2.北京应用物理与计算数学研究所，北京100094

3.中国工程物理研究院高性能数值模拟软件中心，北京100088

CNKI网络出版：2017-04-01,http://kns.cnki.net/kcms/detail/11.2127.TP.20170401.0914.054.html

1 引言

在可视化领域，大规模数据的高速乃至实时绘制问题一直是学者们关注的热点。近年来，高性能计算机性能不断攀升、使用日益广泛，导致应用领域产生的可视数据规模越来越大。例如在一个基于数千上万核上的数值模拟问题中，单时步产生的模拟结果数据量已可达GB量级，完整模拟过程产生的结果数据更是可达TB量级[1]。如何快速有效地绘制如此规模的可视数据，已成为可视化领域的一项重大挑战。

在众多绘制加速技术中，层次细节模型（Level-Of-Detail，LOD）技术是其中较为有效的一种，其相关的理论基础早在科学可视化以串行计算为主的时期便已提出。LOD技术处理的对象是网格模型，其基本思想是在满足观察者对分辨率要求的前提下，构建网格模型的简化模型替代原始模型予以显示，从而降低图形硬件处理的可视数据量，提高模型的绘制速率。常见的LOD技术分为静态与动态两种[2]。静态LOD技术预先生成模型的多级层次细节表示，仅在绘制阶段调用所需显示的模型，该策略往往在绘制阶段效率较高，但多级模型的存储导致了较高的存储开销。动态LOD技术则在绘制中根据视点需求实时生成简化模型，避免了多级模型存储导致的高存储空间占用，但实时的模型生成带来了较大的时间开销，导致动态LOD技术在实际场景中的绘制效率较低，甚至难以满足应用需求。

可视化技术发展至今，已逐步迈入并行可视化的时代，这为提高动态LOD技术的时间性能提供了机遇，即，将动态LOD构建算法并行化，从而大幅提高实时模型生成的速率，使之可满足实际应用场景下的交互帧率绘制需求。为此，本文提出并实现了一种基于区域分解技术的并行动态LOD构建算法，本文将系统地介绍该算法的设计与实现原理，并在最后对算法的应用效果及性能做分析与评测。实验结果表明，相比串行动态LOD构建算法，该算法在保证LOD模型及其图像的质量的前提下，大幅度地提高了动态LOD构建的时间性能，且具备较为理想的并行加速比及可扩放性，能满足动态LOD构建环境下的应用需求。

2 相关工作

近年来诞生了许多有关LOD技术性能优化的研究成果，大致可分为两类，一类是非并行的直接性能优化方法，另一类则是将串行过程并行化的并行优化方法。

直接性能优化法面向LOD构建与调度过程中的不同阶段，或特定的数据类型及应用场景，设计了各种不同的非并行优化算法。一些学者研究了LOD构建中关键技术的优化，即网格简化技术的优化。Nan等设计了以顶点聚类为元操作的简化算法[3]，相比基于几何元素删除的简化算法，有效地提高了算法中元操作的执行速率。Boubekeur等则在顶点聚类算法的基础上引入了基于随机采样的预处理策略[4]，进一步提升了算法的时间性能。Li等在顶点聚类算法的基础上引入了八叉树结构[5]，在提升算法性能的同时克服了顶点聚类算法保拓扑能力差的缺点。Zhao等[6]在研究点云数据快速处理与绘制时，设计了一种基于Retinex理论的点采样算法，用于加速点云数据网格的简化过程。还有一些学者研究了面向特定数据类型与应用场景的优化技术。Zinsmaier等研究了构建点线图的LOD表示的相关算法[7]，提出了基于点聚类与边聚类的LOD构建算法及相应的模型调度准则，有效地提高了点线图LOD构建与调度的速率。Filip等[8]研究了数字高程模型的连续LOD构建与表示。Biljecki等[9]则研究了LOD技术在城市三维场景绘制中的应用问题。

并行优化法同样面向LOD构建与调度中的不同阶段，以及特定的数据类型及应用场景，挖掘算法中可并行化的点并转化为有效的并行程序。与非并行化优化研究的关注点相类似，面向LOD构建中网格简化技术的并行化研究是其中一个重要的研究方向。Lu等研究了基于分布式集群的并行网格简化技术，提出了面向分布式集群的核外并行网格简化框架[10-11]，并成功应用到了多个实际模型中。Lee等面向GPU级并行优化，提出了一种基于嵌入式树的并行网格简化算法[12]，有效提高了多核GPU的利用率。Ozaki等改进了基于QEM的点对合并式网格简化法，实现了一种核外并行简化算法[13]，Odaker等则改进了基于半边折叠的网格简化法，成功实现了算法在GPU上的并行化[14]，上述这些算法均成功实现了网格简化速率的大幅提升。此外还有一些面向LOD构建全阶段的研究，Hu[15]和Derzapf[16]均研究了视相关渐进网格方法在LOD模型预处理、构建、调度全部三个主要阶段的相关并行技术，Peng等[17]则研究了核外动态LOD模型三个阶段中的并行技术。除以上两方面，还存在一些面向特定数据类型与应用的研究。Rizzi等研究了面向粒子模拟数据的并行LOD可视化技术[18]，Goswami等则研究了面向地形数据的并行LOD可视化技术[19]。

3 算法概述

在静态LOD构建中，较为常用且发展较为成熟的技术是网格简化技术，该技术之所以只用于静态LOD构建中，是因为该技术为保持模型的拓扑结构，需完成大量复杂的计算过程，以确定模型在当次迭代步中最适合删除的几何元素（点、边、面）。然而这一计算过程却是算法时间开销的主要组成部分。将网格简化算法直接用于动态LOD构建中，则由于算法本身的时间开销过大，导致模型切换所需的时间过长，从而出现画面停滞或空白间断的问题，无法满足应用需求。

1996年，Hoppe在网格简化技术的基础上提出了渐进网格（Progressive Mesh，PM）方法，克服了传统网格简化方法的困难，将动态LOD技术推入了实用化。该方法包含两个主要过程：（1）基于网格简化的预处理：对原始模型执行一次极大程度的网格简化，并记录简化算法每一次迭代中的有效信息，以及最终得到的最简化网格。（2）网格重建：根据记录的操作信息，在最简化网格基础上重构所需精度的网格。所谓极大程度的网格简化，是指将网格简化至能保持人类可识别出该模型的最低精度，即得到了最终的最简化网格。而有效信息则是指网格简化算法经过大量计算而最终得到的对模型几何元素做出修改的信息，如某次迭代中要删除或修改的点、线、面等。

在动态LOD技术中，渐进网格法采用网格重建的手段实时生成LOD模型，避免了直接使用网格简化算法所需完成的大量计算，有效地降低了算法的时间开销。在串行计算环境下，渐进网格法使得一些较小规模（包含105以下量级三角面单元）的网格模型的在交互帧率下的动态LOD模型构建成为可能。然而在面对大规模网格模型（包含105及以上量级三角面单元）时，却仍无法满足交互帧率绘制需求。

为改善渐进网格法在面向大规模数据时的时间性能，本文基于渐进网格动态LOD构建算法，结合三维模型区域分解技术，提出了一种有效的并行动态LOD构建算法。算法主要包含以下三个步骤：（1）原始模型的区域分解；（2）基于网格简化的并行预处理；（3）并行网格重建。算法主要具备如下优势：（1）可取得理想的次线性加速比，具备一定的实用性；（2）适用于较大的问题规模，具备良好的可扩放性；（3）不受视点变换的影响，适用于动态LOD环境。关于这三点优势的分析将在第6章中给出。此外，本文并没有采用传统的基于能量评估函数的渐进网格方法，而是实现了基于二次误差测度（Quadric Error Metric，QEM）网格简化算法[20]的渐进网格方法。

4 渐进网格方法

如第3章所述，渐进网格方法实质上是网格简化算法应用于LOD构建中的一种优化策略。它包含两个主要的过程：（1）基于网格简化的预处理；（2）网格重构。在预处理过程中，采用不同的网格简化方法将导致不同的渐进网格表示，本文实现了基于QEM网格简化算法的渐进网格方法，从而改变了传统的渐进网格法基于能量函数优化法的实现。本章将依次介绍渐进网格法的基本流程、表示及两个主要过程。

4.1 基本流程

渐进网格法的基本执行流程如图1所示，算法首先通过基于网格简化的预处理过程提取出原始模型的渐进网格表示，然后在动态LOD调度过程中利用渐进网格表示完成实时的网格重建。

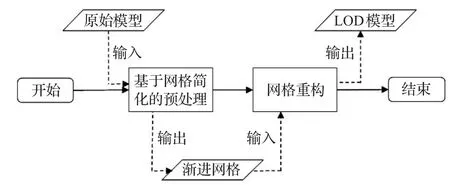
图1 渐进网格方法的基本执行流程图

4.2 改进的渐进网格表示

渐进网格PM表示为由一个极大程度简化的基准网格M0和一个用于重建网格的记录R={r1,r2,…,rn}所构成的整体，其中每条记录ri由具体采用的网格简化算法来决定。例如采用的简化算法是点删除与三角化结合的方法[21]，则ri={vri,T}，T={t1,t2,…,tm}，其中vri表示第i次迭代操作删除的点，即在网格重建中需恢复的点。集合T则表示本次迭代中对产生的多边形洞孔三角化产生的三角面单元集合，即在网格重建中需删除的三角形面单元构成的集合。

Hoppe在提出渐进网格时使用基于能量函数的边折叠算法[22]作为网格简化算法，因此采用边折叠算子描述渐进网格表示。而渐进网格则是基于QEM算法实现，该算法用于改变模型拓扑的基本操作是名为点对收缩的操作，因此本章采用点对收缩算子来给出渐进网格表示的具体描述。

首先给出点对收缩操作的定义。如图2所示，点对收缩即一对顶点收缩为一个顶点的过程，可简洁地表示为公式(v1,v2)→vˉ，该公式包含了以下步骤：（1）将顶点v1与v2合并为一个新的顶点vˉ，并为vˉ选择合适的位置；（2）将所有原本以v1、v2为顶点的三角面的相应顶点指向vˉ；（3）删除全部退化的三角面。在QEM算法中，点对收缩可人为允许距离限定范围下的无边点对收缩，此时将获得较高的时间性能，而模型的拓扑改变会较为严重。

图2 点对收缩的示意图

每条记录ri用于记录点对收缩操作中的有效信息，可形式化表示为ri={v1,v2,vˉ,T1,T2}，Ti={ti1,ti2,…,tin}，i=1,2。其中v1、v2为收缩前的点，vˉ为收缩后的点，T1为需更改顶点指向的三角面集合，T2为退化三角面的集合。

4.3 预处理与重构过程

渐进网格法的预处理过程即利用某种网格简化算法对原始模型执行一个极大程度简化，并记录每一个迭代步对网格拓扑修改所需执行的操作。记原始模型为M，点对收缩算子为vconi，同时沿用4.2节的记号，则预处理过程如图3所示。

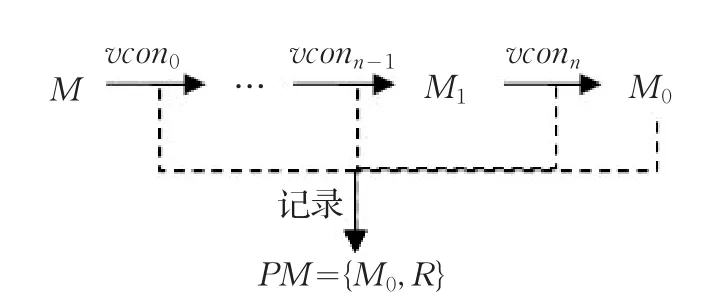
图3 渐进网格方法的预处理过程

重构过程则是一个相反的过程，它相当于对基准网格M0执行一系列点分裂操作。且重构过程往往根据需求执行有限步操作以获取所需精度下的简化模型，记执行了k次点分裂操作所得到的简化模型为Mk，并记点分裂算子为vspliti，同时沿用上文已给出的记号，则重构过程如图4所示。

图4 渐进网格方法的重构过程

此外，在预处理过程中，保持人类可识别出模型的最低精度通常与模型本身的数据规模、形状等因素有关，而这些因素的分析是拓扑学中的一项难题。因此用于描述极大程度的因子在实际应用中往往根据经验人为指定。

4.4 简化率计算

在动态构建LOD模型时，需根据当前视点信息确定模型重构所需达到的精度。简化率便是用于间接描述该精度的一个小数。简化率ε用于描述LOD模型较原始模型的简化程度，其定义为LOD模型中的单元总数除以原始模型中的单元总数，ε的计算结果是一个小数，其取值在闭区间[0，1]中。

简化率需根据当前视点的信息完成计算，本文沿用了文献[15]中给出的计算方法，即利用视锥、表面法向与屏幕空间几何误差三重评判标准的计算方法。具体可查阅该文献，本文不再赘述。

5 自适应区域分解算法

在计算机辅助设计与图形学领域，区域分解是指将二维或三维模型采用一种或多种分割技术切分为多个相互独立且边界闭合的子模型的过程[23]。其中较为常用的一种分割技术是基于几何曲面的切割技术，几何曲面可为隐式或显式的各种自定义曲面，较为实用的曲面则是简单的球面或平面。

本文的工作是利用区域分解技术将原始模型分割为多个互不依赖的子区域，使得算法可在这些子区域上并行执行。为切合并行算法，本文采用了基于平面切割的区域分解方法。本章将简要介绍区域分解的概念，并介绍一种基于模型包围盒的自适应区域分解算法。

5.1 基于平面分割的区域分解

基于平面分割的区域分解技术是利用一系列切割平面，将原始模型分割为多块子区域的技术[20]。该技术主要包括两个过程：（1）分割面计算；（2）平面剪裁。

过程（1）采用手动或自动的算法选取一系列由方程Ax+By+Cz+D=0确定的平面。过程（2）则依次利用每个分割面对当前模型执行平面剪裁操作。需要注意的是，平面剪裁操作除完成单元与分割面求交、单元分割、边界缝合等基本操作外，还需完成正确识别并划分切割所得各个子区域的过程。这一过程也是保证并行算法得以正确执行的关键。

5.2 模型包围盒

在介绍自适应区域分解算法之前，首先介绍模型包围盒（bounding box）的概念，它是自适应区域分解算法计算分割面的依据。

包围盒是一个能包罗整个模型的最小长方体。在三维欧式空间中，取模型中Ox,Oy,Oz方向上最大的三个值xmax、ymax、zmax，及最小的三个值xmin、ymin、zmin，根据这些值建立两个点vmax=(xmax,ymax,zmax)、vmin=(xmin,ymin,zmin)。由这两个点所构造的长方体即包围该模型的最小长方体，也即模型的包围盒。图5给出了一个飞机模型的包围盒（bounding box）示意图，图中包罗整个飞机模型的长方体即包围盒。

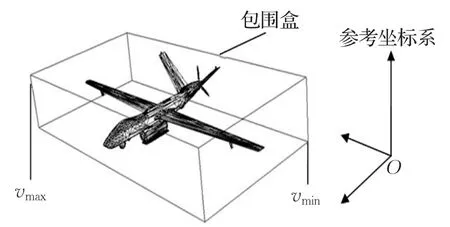
图5 飞机模型的包围盒示意图

在本文的区域分解算法中，利用包围盒可精确确定模型所处的有效范围，从而能够快速确定所需分割面的法向量。

5.3 自适应区域分解算法

本文设计的区域分解算法可根据模型的包围盒信息与相关输入参数自动计算分割面，并产生所需的分解结果。在分割面计算中，将求出三个分割面集合S1、S2、S3，这三个集合实际上分别对应了法向量与坐标轴Ox,Oy,Oz相平行的所有分割面，因此在同一集合中，全部平面的法向量是相同的，而在不同集合中，平面之间的法向量则是相互垂直的。

记Ox,Oy,Oz方向上的分割参数分别为m,n,p，沿用5.2节给出的记号，描述具体的分割面计算方法如下：

算法自适应分割面计算算法

输入：分割参数m,n,p、原始模型。

输出：分割面集合S1、S2、S3。

算法描述：

（1）求出原始模型的包围盒最大最小点vmax、vmin。

（2）作向量vminvmax，求出其分别在Ox,Oy,Oz上的分量，记为nx、ny、nz。

（3）求解集合S1。先求出线段xminxmax的m-1个m等分点v11、v12、…、v1(m-1)，分别用这m-1个点与法向量nx结合，求得m-1个分割面s11、s12、…、s1(m-1)，加入集合S1中。

（4）用同样的方法，求出线段yminymax的n-1个n等分点、线段zminzmax的p-1个p等分点，并分别结合法向量ny、nz，求得n-1个分割面加入集合S2，及p-1个分割面加入集合S3。

求得了所需的分割面，算法将逐一利用每个分割面对原始模型做平面剪裁。根据不同分割面集合中的平面相互正交的性质不难看出，原始模型被剖分为m×n×p个子区域。图6给出了一个对航母模型做简单区域分解的结果示意图，在该图中m、n、p取值均为2。

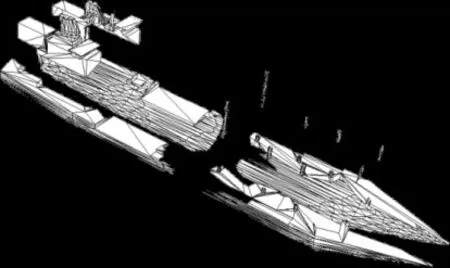
图6 航母模型区域分解结果示意图

6 并行动态LOD构建算法

前文已经分别描述了动态LOD构建的核心算法——渐进网格法，以及形成有效并行计算区域划分的自适应区域分解算法。本章将给出由上述两种方法结合所形成的并行动态LOD构建算法的完整描述。

6.1 并行动态LOD构建算法

本节给出完整的并行动态LOD构建算法的描述，该算法由两个算法组成。其中算法1是预处理过程的并行化算法，即利用网格简化算法并行地生成原始模型的渐进网格表示，该算法为每个子模型生成一个独立的渐进网格表示；算法2是重构过程的并行化算法，即在实际LOD应用场景中，基于原始模型的渐进网格表示的并行LOD模型重构过程。

下面给出算法1及算法2的具体描述，其中沿用了第4章、第5章所给出的记号。

算法1并行预处理算法

输入：并行参数m,n,p、并行核数k、原始模型M。

输出：m×n×p个子渐进网格PMi,i=1,2,…,m×n×p。

算法描述：

（1）根据并行参数，求出3个分割面集合S1、S2、S3。

（2）根据集合S1、S2、S3，将M划分成m×n×p个子模型Mi。

（3）采用6.2节中描述的负载分配算法，将m×n×p个子模型分配至k个CPU核上，并行生成子模型的渐进网格表示PMi。

（4）并行保存每个PMi。

算法2并行LOD模型重构算法

输入：并行核数k、视点信息、m×n×p个渐进网格表示PMi。

输出：原始模型的LOD模型。

算法描述：

（1）在0号CPU核上，根据视点信息，计算出简化率ε。

（2）在k个CPU核上，采用6.2节中描述的负载分配算法，根据简化率ε，并行为每个PMi生成LOD模型。

6.2 负载分配

在并行程序中，子数据块个数与CPU核数往往是不相等的。因此并行算法需解决将m块数据分配给n个CPU核的问题。

本文采用了一种均匀负载分配的策略，该策略描述如下：（1）当m=n时，为每个CPU分配一个基准网格；（2）当m＜n时，为前m个CPU各分配一个基准网格，后n-m个CPU不分配基准网格；（3）当m＞n时，设i=m/n,p=m mod n，首先为每个CPU分配i个基准网格，余下的p个基准网格分配给前p个CPU。在实际应用中很少出现m＜n的情形。此时一种更为有效的做法是将数据继续划分为n块。

6.3 算法优势

本文提出的并行动态LOD控制算法实质上是一种数据级并行算法，相比功能级并行与流水线式并行算法[24]，数据级并行算法在实际应用中具有较强的优势。

面对特定的应用领域，只要能找出一种有效划分原始数据的算法，并充分顾及子数据块之间的相互影响，便能设计出有效的并行程序，这导致了数据级并行算法是较为容易设计与实现的。此外，并行程序旨在应用于数据规模较大的情形，而对于实际应用中的许多数据，在数据规模较大时，往往能划分为较高数目的子数据块，从而使得数据级并行算法能利用较高数目的CPU核实现并行计算。相比之下，功能级并行算法往往只能将串行算法流程中有限的程序块并行化，如果该程序块本身只占据算法执行时间的一小部分，亦或该程序块只能取得较小的并行度，则直接导致了该并行算法的性能低下。而流水线式并行更是取决于算法步骤的划分及步骤之间的依赖关系，在所有并行算法中设计难度最高。此外，上述两种并行算法因设计难度高，往往不具备高稳定性，导致难以适用于CPU核数较多的情形。

7 实验结果

本章将从LOD模型的绘制效果和算法的并行性能分析两个角度对算法作出评价。实验中使用的环境为浪潮TS10K集群，该机包含16个计算节点，每个节点包含2颗E5-2600系列处理器，每个处理器包含12颗Intel Xeon E5-2692v2（2.20 GHz）/8.0GT/30ML3/1866 CPU核，节点内存为8 GB。

7.1 模型效果

本章将依次展示模型的基准网格及动态LOD构建生成模型的绘制效果，并做相应的统计分析。将看到区域分解给模型带来的影响。

7.1.1 基准网格绘制效果

由前文可知，区域分解技术在分割模型时会做一系列边界缝合操作，使得分割获得的子模型相互之间不存在数据依赖关系的同时保持了边界闭合性质，从而保证了模型整体的几何构型不发生变化。然而对原始模型做不同程度的区域分解，除产生不同的分解结果之外，还导致了子区域的边界发生变化。这种分割结果及子区域边界的变化，却直接导致了为子模型生成的基准网格的变化。

图7给出了将一个包含96 537个三角面单元的航母模型，做不同程度的区域分解所产生的基准网格的绘制效果图。其中图7（a）是未简化的原始网格模型，图7（b）是对未做区域分解的模型直接生成基准网格的结果，图7（c）～（i）则是在人为指定区域分解参数m、n、p的情况下，将原始模型做不同程度区域分解并生成基准网格的结果。生成所有基准网格预设的简化率均为0.002。

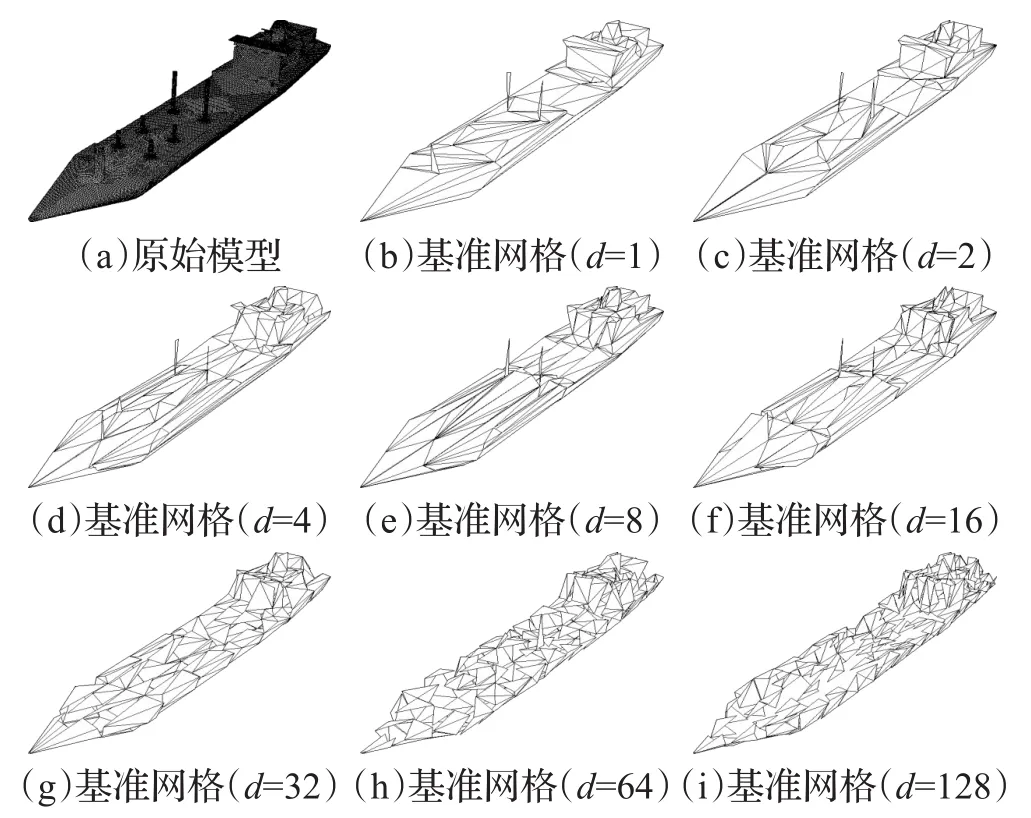
图7 航母模型在不同程度区域分解下的基准网格

对比图7（b）～（i）可以看出，在不同的区域分解结果所生成的基准网格的拓扑结构之间存在明显的差异，且这一差异的分布恰好与区域分解所形成的子区域分布相对应。事实上，在子区域数d固定时，选取不同的分割面也会产生不同的效果。然而实际应用中为尽可能确保分配给每个区域的网格单元数目的接近，往往会根据对原始模型的直观观察人为选取适合的分割面，即人为指定参数m、n、p的值，而图7中展示的结果便是人为选定较优的参数所形成的结果。

表1中给出了对这些参数取值的一个统计。从m、n、p值的统计中可以看出，随着子区域数的增长，m、n、p参数的取值具备一定的变化规律，即首先增加n的值，然后增加m的取值，而p的取值则始终为1。如前文所述，选取这些参数值是根据对该模型的直观观察，选取确保能产生较均衡负载分配的分割平面。根据人的直观观察往往是快速而有效的，例如可以很容易发现，在子区域数d=2时，沿航母模型的对称线一分为二是最合理的分割方法。随着所需分割区域数的增长，总是会人为确定参数m、n、p的取值，这是一种较为便捷的方式，同时也避免了随意选取参数导致较差的计算结果带来的计算资源的浪费。此外，从三角单元数一栏可发现，随着子区域数d的增加，基准网格模型的单元数出现小幅度的增加。这是因为所做的分割操作越多，缝合边界所形成的新单元就越多。随着简化率逐渐减小，这一差距会逐渐加大，但这一影响在LOD模型重构过程中是几乎可忽略的，将在7.1.2小节给出相应的分析。

7.1.2 动态LOD模型绘制效果

分别对飞机模型和航母模型做了动态LOD模型构建生成实验，对每个模型，将模型分别分解为1、2、4、8、16、32、64、128个子区域，并为每种划分分别生成4组具有较高展示度的结果模型。这里所说的高展示度，是指能让用户通过对比明显地看出模型之间具有不同的精度的一组结果，因此这里ε的取值只是为了形成具有一定对比度的绘制结果。此外，原始的飞机模型包含252 725个三角面单元，原始的航母模型包含96 537个三角面单元。

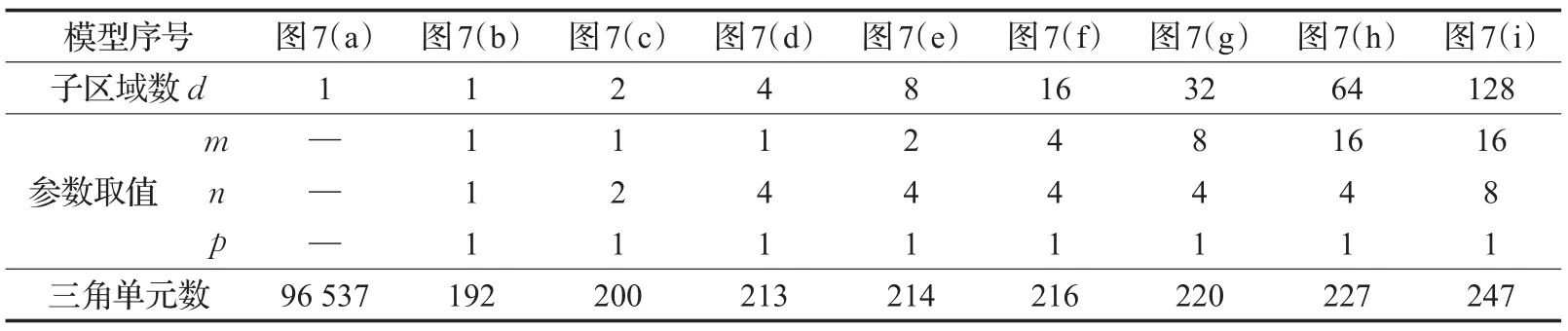
表1 航母模型在不同程度区域分解下的统计信息

因篇幅限制，图8、9仅给出了两种模型分解为64个子区域时的绘制效果图。其中图（a）展示原始模型，图（b）～（e）展示不同简化率下的LOD模型，图（f）展示模型在图（e）中LOD模型的面填充绘制结果。在图8（b）～（e）及图9（b）～（e）这8幅子图中存在区域分解对网格模型产生的剖分线，较为容易识别的是图8（e）中飞机两翼上的剖分线，而航母模型的剖分线则难以同模型本身简化产生的网格线相区分。对比图（b）～（e）可以看出，随着简化率ε的增长，LOD模型的网格越来越简洁，但模型的基本结构依然保持较好，这是因为预处理过程中采用网格简化算法最大限度地保持了模型的拓扑结构。当两种模型简化到图（e）所对应的简化率时，模型的填充图依然可以提供较好的绘制效果。

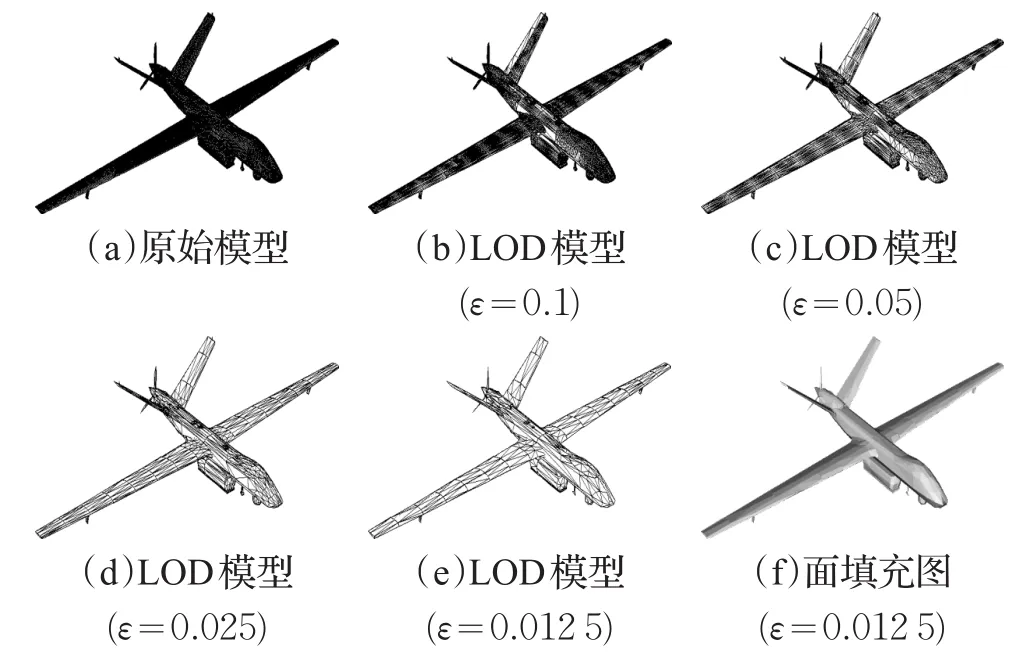
图8 飞机模型在d=64时ε取不同值的效果图

图9 航母模型在d=64时ε取不同值的效果图

表2、表3则给出了分别对两个模型所做的8组完整实验的统计，统计的是在子区域数d取不同值时，生成的LOD模型所包含的三角单元数。横向观察表格的每一行，可发现模型的单元数具有随d的增加而增长的规律，但增长幅度非常小。图10中直观地展示了三角单元数随d增加的变化趋势，随着d的增大，单元数始终呈增长的趋势，但增长幅度极小，几乎可忽略不计。导致这一现象的原因是模型都是表面型网格模型，因而区域分解中边界缝合操作增加了模型的单元数目，但并没有增加太多的单元，与7.1.1小节中分析的结论一致。

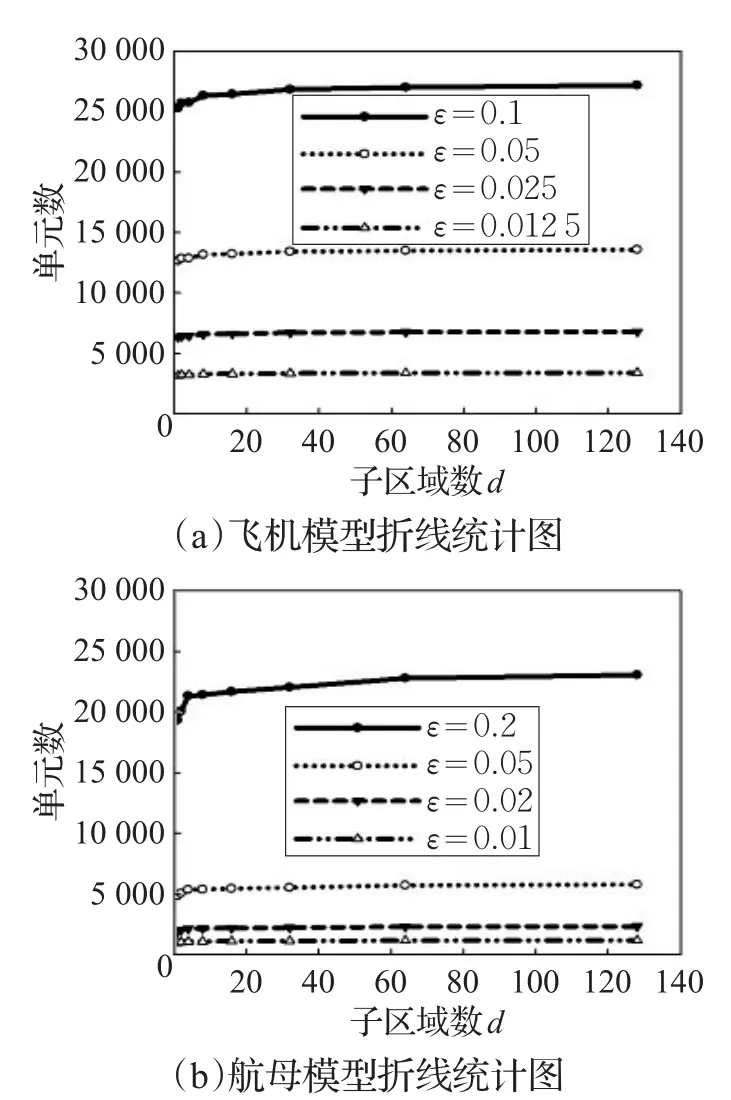
图10 两种模型网格单元数的折线统计图

7.2 并行性能测试

本节将测试算法的时间性能，包括并行加速比a和并行效率E。并行加速比和效率的定义如下：

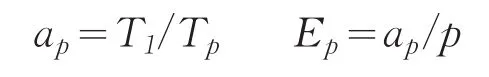
其中ap为并行加速比、Ep为并行效率、p为并行计算使用的CPU核数、T1为串行算法执行时间、Tp为使用p个CPU核的并行算法执行时间。

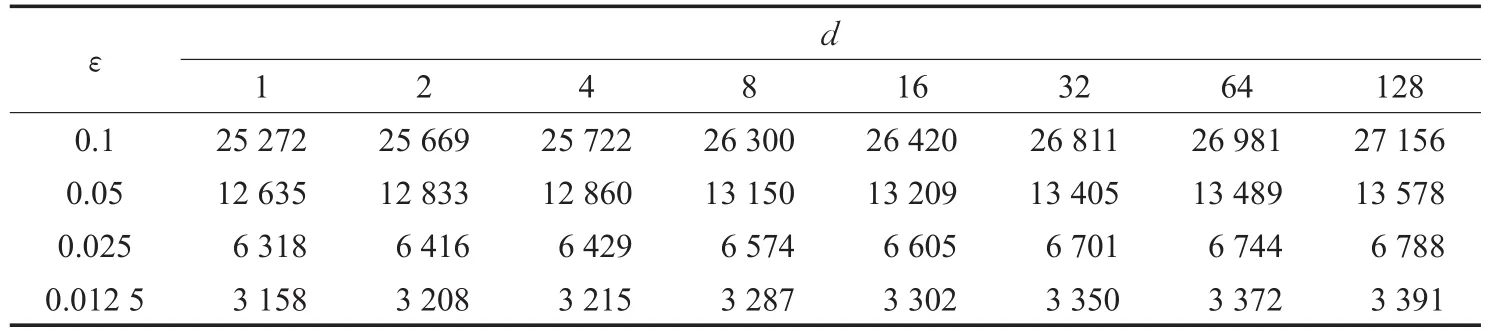
表2 飞机模型的动态LOD模型网格单元数统计结果

表3 航母模型的动态LOD模型网格单元数统计结果

分析渐进网格方法不难发现，算法执行的最坏情形是ε=1的情形，即直接由基准网格M0重构出原始模型网格M的情形，此时算法做了最多次点分裂操作，为证明算法具有较高的时间性能，需完成该情形下的测试。此外选择ε=0.5、ε=0.25的两个情形做了测试。

实验中选取了分别包含三角单元数为252 725、1 263 625、6 318 125的三个真实航母模型做测试算例，分别基于8个指数级增长的CPU数在上述3个简化率下执行了算法，其区域分解参数设置与表1中设置的相同。算法的执行时间统计在表4中。其中，n代表模型包含的三角单元数，p代表并行算法使用的CPU核数，ε仍表示简化率。

从表4中可以发现，随着CPU核数p的增加，算法的执行时间明显降低。该规律表明本文的并行算法是有效的。根据表4，计算了算法的加速比及并行效率，并做了相应的统计图。图11、12分别给出了算法的加速比及并行效率的折线统计图。

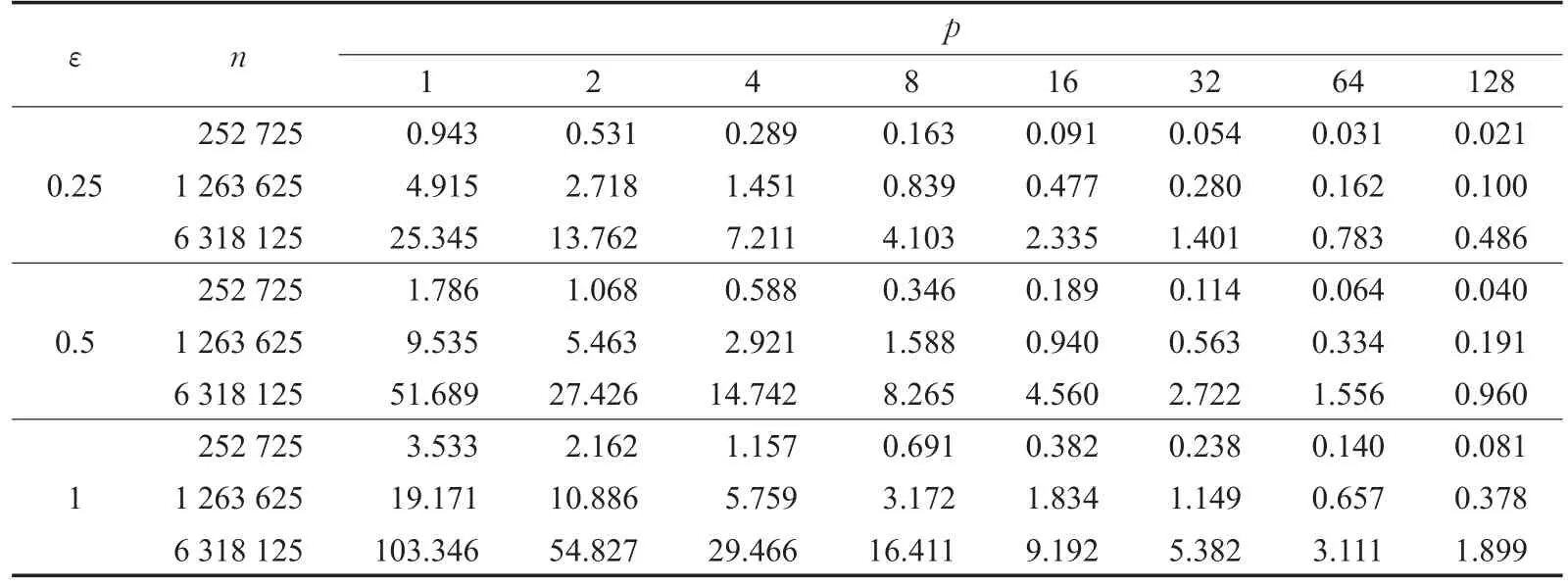
表4 算法并行执行时间统计表s

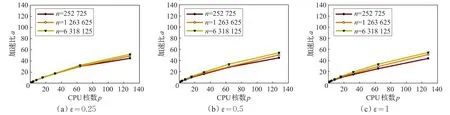
图11 ε取不同值时算法的加速比

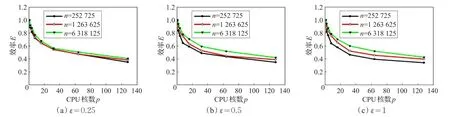
图12 ε取不同值时算法的效率

单独观察图11中的每幅子图可以看出，在简化率ε取不同值的情况下，随着CPU核数p的增加，算法的加速比也得到了适当增大，但加速比增长趋势逐渐变缓。然而规模n较大的算例的加速比总是大于规模较小的算例，说明算法适用于问题规模较大的情形。对比图11中的三幅子图则发现，随着简化率ε的增加，加速比并无发生明显的变化，也即视点变换不会对算法性能造成影响，说明算法适用于任意精度的两个LOD模型之间的转换。实际上ε取不同的值仅仅影响算法执行的元操作的个数，因此ε不应影响算法的性能。

单独观察图12中的每幅子图可以看出，在每种简化率取值下，随着CPU核数p的增加，算法的并行效率逐渐降低，这与算法加速比随着p的增加而增长逐渐变缓相符合。同时对于规模n较大的算法，并行效率近似总是大于规模较小的算例，同样说明了算法适用于问题规模较大的情形。对比图12中的三幅子图则发现，简化率ε的增加对并行效率并无明显的影响，与加速比中的相关分析也相吻合。

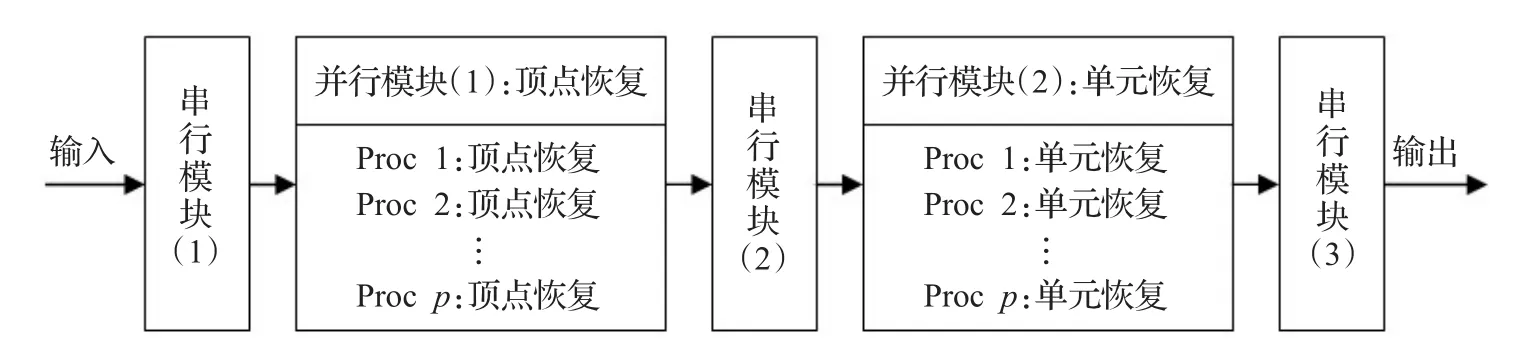
图13 功能级并行算法框架图

7.3 并行算法性能对比

本节将给出本文算法与功能级并行算法及流水线式并行算法性能的分析对比。首先给出功能级并行算法与流水线式并行算法的概述。顾名思义，两种算法均是通过改进算法的执行流程来达到并行效果。功能级并行算法框架大致如图13所示。

该方法改变了传统重构过程的思路，将元操作中的两个主要子操作（顶点恢复、单元恢复）分离出来，在相应串行模块中消除操作之间的依赖，从而可将这两个子操作分别并行化执行。两个并行模块所能达到的最高并行度由传统算法中的元操作数目决定。流水线式并行算法架构大致如图14所示。

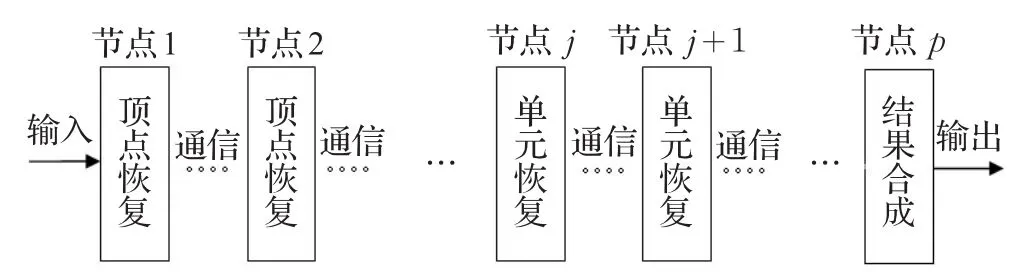
图14 流水线式并行算法框架图

该方法同样分解了传统的重构过程，并将顶点恢复与单元恢复操作进一步分解为多个相同的子过程，从而增加了流水线的节点数。同时该方法需要模型的区域分解结果作为支撑，使得p个节点能同时工作。

先给出理论上的对比分析。在输入数据及使用CPU核数目相同的前提下，本文提出的数据级并行算法可对p个CPU核上的数据实现算法全阶段的并行化处理，相比之下，功能级并行算法只是对算法的部分阶段实现了并行处理，其余阶段继续保持串行执行。而流水线式并行算法虽是全阶段并行化算法，但却因节点间的通信而引入了许多通信开销。因此可认为本文提出的数据级并行算法结合了另两种算法的优点，具备最好的时间性能。下面将通过一组实验进行验证。

实验中依然选取了分别包含三角单元数为252 725、1 263 625、6 318 125的三个真实航母模型做测试算例，分别基于8个指数级增长的CPU核数在简化率为0.5的条件下执行了三种不同的并行算法，且区域分解参数设置仍与表1相同。三种算法的执行时间统计如表5所示。

直接观察表5可以看出，在相同规模n与CPU核数p下，几乎总是本文算法的执行时间最快，而流水线式并行算法的执行时间最慢。在图15中，对三种算法在不同问题规模下的执行时间做出了柱状统计图。从图中可以看到，在不同问题规模及CPU核数下，本文算法的执行时间总是优于另外两种算法，和上述理论分析的结果相一致。

此外，从图中可发现功能级并行算法的执行时间又比流水线式并行算法的执行时间快一些，即功能级并行算法中串行模块的时间开销小于流水线式并行算法中的节点通信开销。导致这一现象的原因是在动态LOD算法中，顶点恢复与单元恢复两个子操作占据了算法的相当大部分的时间开销，从而使得功能级并行算法中串行模块的执行时间占比小于流水线式并行算法中的通信时间占比。事实上，在其他一些问题的并行化算法中，流水线式并行算法的时间开销也会高于功能级并行算法的时间开销，这与所面对的问题及算法的设计等因素有关。

表5 三种并行算法执行时间统计表s

图15 三种算法执行时间柱状统计图

8 总结与展望

本文面向大规模科学数据的高速绘制问题，改进传统的基于渐进网格的动态LOD构建算法，研究并实现了一种基于区域分解技术的并行动态LOD构建算法。

本文主要做了如下贡献：

（1）实现了一种基于QEM网格简化法的渐进网格方法。

（2）提出了一种自适应区域分解算法。

（3）设计并实现了一种基于区域分解的并行动态LOD构建算法。

实验结果表明，本文提出的算法主要具备如下几点优势：

（1）可取得理想的次线性加速比，具备一定的实用性。

（2）适用于较大的问题规模，具备良好的可扩放性。

（3）相比功能级并行算法和流水线式并行算法，本文算法具备更好的时间性能。

（4）不受视点变换的影响，适用于动态LOD环境。

在未来的工作中，还可展开两点研究：

（1）现阶段的重构算法所重构的模型是视独立的模型，即模型全局基于相同的精度。未来可研究视相关的重构算法，即重构所得的模型在距离视点越近，精度越高。在实际应用中，单一模型往往生成视独立LOD模型较多，而视相关LOD模型往往面向复杂场景或地形数据而构建。

（2）进一步挖掘渐进网格生成与重构算法中的功能并行性，研究数据与功能两级混合并行算法。

[1] 王弘堃，肖丽，邵京云，等.面向大规模科学计算的可视分析模式[J].计算机工程与科学，2012，34（8）：142-146.

[2] Luebke D，Reddy M，Cohen J D，et al.Level of detail for 3D graphics[M].[S.l.]：Elsevier Science Inc，2002.

[3] Nan L，Gao P，Lu Y，et al.A new adaptive mesh simplification method using vertex clustering with topologyand-detail preserving[C]//International Symposium on Information Science and Engineering，2008：150-153.

[4] Boubekeur T，Alexa M.Mesh simplification by stochastic sampling and topological clustering[J].Computers&Graphics，2009，33（3）：241-249.

[5] Li J，Chen Y.A fast mesh simplification algorithm based on octree with quadratic approximation[C]//International Conference for Young Computer Scientists（ICYCS 2008），2008：775-780.

[6] Zhao Y，Liu Y，Song R，et al.A retinex theory based points sampling method for mesh simplification[J].IEEE Signal Processing Society，2011：230-235.

[7] Zinsmaier M，Brandes U，Deussen O，et al.Interactive levelof-detail rendering of large graphs[J].IEEE Transactions on Visualization&Computer Graphics，2012，18（12）：2486-2495.

[8] Strugar F.Continuous distance-dependent level of detail for rendering heightmaps[J].Journal of Graphics GPU&Game Tools，2011，14（14）：57-74.

[9] Biljecki F，Ledoux H，Stoter J，et al.Formalisation of the level of detail in 3D city modelling[J].Computers Environment&Urban Systems，2014，48（16）：1-15.

[10] Lu Y，Gao P，Chu Q，et al.Parallel implementation of mesh simplification on a beowulf cluster[C]//International Symposium on Distributed Computing and Applications to Business，Engineering and Science，2010：160-164.

[11] Lu Y，Li N，Gao P，et al.A parallel memory efficient framework for out-of-core mesh simplification[C]//IEEE International Conference on High Performance Computing and Communications（HPCC 2009），Seoul，Korea，2009：666-671.

[12] Lee H，Kyung M H.Parallel mesh simplification using embedded tree collapsing[J].Visual Computer，2016：1-10.

[13] Ozaki H，Kyota F，Kanai T.Out-of-core framework for QEM-based mesh simplification[C]//Eurographics Symposium on Parallel Graphics and Visualization，Eurographics Association，2015.

[14] Odaker T.GPU-accelerated real-time mesh simplification using parallel half edge collapses[M]//Mathematical and Engineering Methods in Computer Science.[S.l.]：Springer International Publishing，2015.

[15] Hu L，Sander P V，Hoppe H.Parallel view-dependent level-of-detail control[J].IEEE Transactions on Visualization&Computer Graphics，2010，16（5）：718-728.

[16] Derzapf E，Menzel N，Guthe M，et al.Parallel viewdependent out-of-core progressive meshes[C]//Vision，Modeling，and Visualization Workshop 2010，Siegen，Germany，2010：25-32.

[17] Peng C，Mi P，Cao Y.Load balanced parallel GPU outof-core for continuous LOD model visualization[C]//Proceedings of the 2012 SC Companion：High Performance Computing，Networking Storage and Analysis，2012：215-223.

[18] Rizzi S，Hereld M，Insley J，et al.Large-scale parallel visualization of particle-based simulations using point sprites and level-of-detail[C]//Eurographics Symposium on Parallel Graphics&Visualization，2015：1-10.

[19] Goswami P，Makhinya M，Bösch J，et al.Scalable parallel out-of-core terrain rendering[C]//Proceedings of the EurographicsConferenceonParallelGraphicsand Visualization，2010：63-71.

[20] Garland M.Surface simplification using quadric error metrics[J].ACM Siggraph Computer Graphics，2015，1997：209-216.

[21] Schroeder W J.Decimation of triangle meshes[J].ACM Siggraph Computer Graphics，1992，26（2）：65-70.

[22] Hoppe H.Mesh optimization[J].ACM Siggraph Computer Graphics，1993，27：19-26.

[23] 徐权，崔涛，刘青凯，等.基于区域分解技术的并行四面体网格生成算法[J].计算机工程与设计，2014，35（1）：153-157.

[24] 奎因，陈文光，武永卫.MPI与OpenMP并行程序设计：C语言版——世界著名计算机教材精选[M].北京：清华大学出版社，2004.

WEI Zijin,XIAO Li.Parallel dynamic level-of-detail construct algorithm based on domain decomposition.Computer Engineering andApplications,2018,54（6）：168-177.

WEI Zijin1，2，3,XIAO Li2，3

1.Graduate School of ChinaAcademy of Engineering Physics,Beijing 100088,China
2.Institute ofApplied Physics and Computational Mathematics,Beijing 100094,China
3.CAEP Software Center for High Performance Numerical Simulation,Beijing 100088,China

To solve the problem of fast rendering large-scale visual data,a parallel dynamic level-of-detail construct algorithm based on domain decomposition is presented.The main contributions of this article are presented as follows.Firstly,the traditional progressive mesh algorithm is improved by using quadric error metric method,to provide faster implementation.Then,a self-adaptive domain decomposition algorithm based on model’s bounding box is put forward for cutting the original model into several blocks for parallel computing.Finally,a parallel dynamic level-of-detail construct algorithm by executing progressive mesh algorithm on the blocks in parallel is presented.As a result,this algorithm can generate high-qualified level-of-detail models,and has ideal speed-up ratio and expansibility.Compared to serial algorithms,this algorithm greatly reduces the execution time.

visualization;Level-Of-Detail（LOD）;progressive mesh;domain decomposition;parallel computing

面向大规模可视数据的高速绘制问题，提出了一种基于区域分解的并行动态LOD（level-of-detail，层次细节模型）构建算法。算法首先改进了传统的渐进网格方法，实现了基于二次误差测度网格简化算法的渐进网格方法；接着提出了一种基于模型包围盒的区域分解算法，实现了原始模型的自适应区域分解；在每个子区域上，并行地执行渐进网格方法，实现了模型的并行动态LOD构建。实验结果表明，该算法可生成高质量的LOD模型，具备理想的加速比和可扩放性；与串行算法相比，该算法有效地提高了算法的执行效率。

可视化；层次细节模型（LOD）；渐进网格；区域分解；并行计算

2016-10-24

2017-01-05

1002-8331（2018）06-0168-10

A

TP391.41

10.3778/j.issn.1002-8331.1610-0260

国家重点研发计划项目（No.2016YFB0201302）；计算物理重点实验室基金（No.9140C690504150C69001）。

魏子衿（1991—），男，硕士研究生，研究方向为科学计算可视化，E-mail：18618316878@163.com；肖丽（1971—），通讯作者，女，研究员，研究方向为科学计算可视化。