构造样本k近邻数据的多标签分类算法

乔亚琴，马盈仓，陈红，杨小飞

西安工程大学理学院，西安710048

构造样本k近邻数据的多标签分类算法

乔亚琴，马盈仓，陈红，杨小飞

西安工程大学理学院，西安710048

1 引言

传统的监督学习在单个标签下学习，即每个对象只与单个标签相关联，并且已经提出了多种算法并取得良好的效果[1]。然而，现实世界的对象通常是与多个标签同时关联。例如，在图像分类中，一幅图像可能同时包含树木、山地、日落等多个标签，一首乐曲可能属于“钢琴曲”，也可能属于“古典音乐”，蛋白质可能同时具有多种功能，如“运输功能”、“免疫功能”等。因此，给一个对象或示例赋予一个标签子集，并且在这个基础上进行建模和学习，这就构成了多标签的学习框架，多标签学习的意义在于使得每个示例不仅仅对应于单个标签，而是与多个标签建立对应。多标签学习最初主要是在文本分类[2]领域进行研究，随后将其应用到一些新的领域。比如音乐分类[3]、蛋白质功能分类[4]等。经过近几年的发展，在数据挖掘[5]、多媒体内容自动标注[6]、生物信息学[7]、信息检索[8]、个性化推荐[9]等应用得到广泛的应用。

在算法研究上，已经提出了大量的多标签学习算法。文献[10]将这些算法分为三类：一是“问题转换”方法，其主要思想是将多标签训练样本进行处理，将多标签学习问题转化为已知的学习问题进行求解。比如有一阶方法Binary Relevance[11]、二阶方法Calibrated Label Ranking[12]和高阶方法Random k-labelsets[13]等。二是“算法适应”方法，其主要思想是通过常用监督学习算法进行改进，用于多标签数据学习。比如有ML-KNN[14]、IMLLA[15]、IBLR-ML[16]、Rank-SVM[17]等。三是通过“集成”方法进行多标签学习的算法，比如有ECC[18]、随机森林的预测聚类树[19]等。

在以上学习算法中，ML-KNN算法是目前常用的一种多标签学习算法。该算法通过统计k近邻样本的类别标签信息，根据最大化后验概率来对测试样本的标签进行预测，具有操作简单，运算速度快，结果稳定等优点。本文在对ML-KNN分析的基础上，指出其主要思想是将原始多标签数据集通过统计邻近样本标签得出新的数据集，在此数据集上通过朴素贝叶斯进行分类。在此基础上，由于ML-KNN统计样本未考虑近邻距离对标签的影响，本文在考虑k近邻样本关于测试样本距离的基础上，建立新的数据集。新的数据集特征属性为样本关于k近邻的距离与特定标签的加权和，这样不仅考虑k近邻中包含标签的样本个数，而且考虑了距离的影响，可以更多地获取原始数据集的信息，而特征属性维数大大降低。在新数据集上，建立回归模型，本文主要采用线性回归和Logistic回归，从而对测试样本进行预测。本质上，新数据集是原始多标签数据通过k近邻的信息提取，会漏掉一些信息，因此，为了更好地进行预测，在原始数据集上提取每个标签关于特征属性的Markov边界，连同新数据集的特征属性一起构造回归模型进行多标签学习。这样会包含更多的信息，实验结果也在一定程度上验证了这一点。

2 ML-KNN算法

给定多标签训练集D={(x1,Y1),(x2,Y2),…,(xm,Ym)},其中m表示样本个数，xi∈Rn为n维的属性向量xi=(xi1,xi2,…,xin)T,Yi∈Rq为与xi对应的标签向量Yi=(yi1,yi2,…,yiq)T,q表示标签个数，yij∈{+1,-1},i=1,2,…,m,j=1,2,…,q。若yij=+1，则表示样本xi的具有第j个标签，反之则不具有j标签。下面用yj表示第j个标签。一般的，对于样本x∈Rn，为了方便，用Y(x)=(y1(x),y2(x),…,yq(x))T表示x的标签向量，若yj(x)=+1，则表示样本x的具有yj标签。用N(x)表示样本x在D中k个近邻构成的集合，其中

样本间的相似度采用n维空间两点间的Euclidean距离的倒数来刻画。对于第j(1≤j≤q)个标签yj而言，ML-KNN算法统计如下的值：

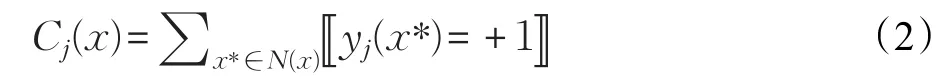
ML-KNN算法是通过k近邻统计每个样本的Cj(1≤j≤q)，得到新的特征属性，建立每个样本的Cj与标签集的对应关系。

设有如表1的多标签数据集，对每一个样本计算其5近邻，比如对样本x1，可以计算其5近邻N(x1)={x6,x7,x3,x9,x8}，统计其具有标签y1的个数有4个，包含标签y2的个数有1个，包含标签y3的个数有3个，从而C1(x1)=4,C2(x1)=1,C3(x1)=3。对于其他样本，类似的也可以计算出。由此可以得到如表2的新数据集，其在统计k近邻的角度提取了原始数据集的信息。

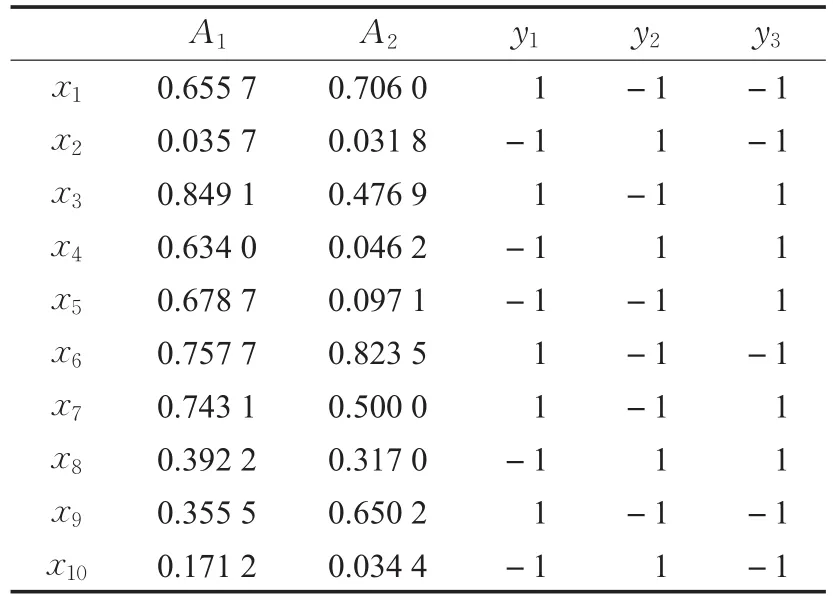
表1 一个2属性3标签的数据集

表2 统计5近邻标签个数的新数据集

在新数据集上，ML-KNN是如何进行多标签学习的呢，从以上分析可以看出，Cj所刻画的信息对于预测标签yj来说具有强相关的作用，因此通过Cj与yj建立朴素贝叶斯模型进行分类，就可以得到ML-KNN的多标签学习算法。

由以上分析可以看出，通过k近邻构造新的数据集，新数据集本质上进行了特征提取。ML-KNN即通过Cj的信息估计yj，取得很好的效果。但是，从另一方面，ML-KNN仅通过Cj的信息估计yj，没有考虑新数据集中其他属性对分类结果的影响，因此一定程度上有信息的丢失。文献[15]基于这种情况进行改进，综合考虑新数据集的全部属性特征，提出IMLLA算法。它是对k近邻构造的新数据集利用线性回归模型来进行多标签分类，在学习效果上有了显著的提高。由于原始数据集一般属性的个数都远远大于标签的个数，而新数据集属性的个数与标签个数相同，属性的维度有了大幅的降低，因此，在新的数据集上进行多标签回归学习可以得出比原始数据集更好的结果。

3 考虑k近邻样本距离的多标签学习算法

由上一章可以看出，ML-KNN通过统计k近邻的标签个数来进行分类。实际上，对测试样本x，其k近邻中样本与x的距离远近对于x的标签也具有很大影响。考虑仅有1个标签的情形，如图1所示，给出x的10近邻，实心点表示具有标签，空心点不具有标签。可以看出，10近邻中不具有标签的个数为6个，具有标签个数为4个。如果仅考虑个数，x应该不具有标签。但可以看出具有标签的样本距离x较近。从直观上，x应该具有标签。因此，距离的远近影响分类的结果。在数据转化过程中，不仅要考虑k近邻中包含标签的个数，同样要考虑样本间的距离。

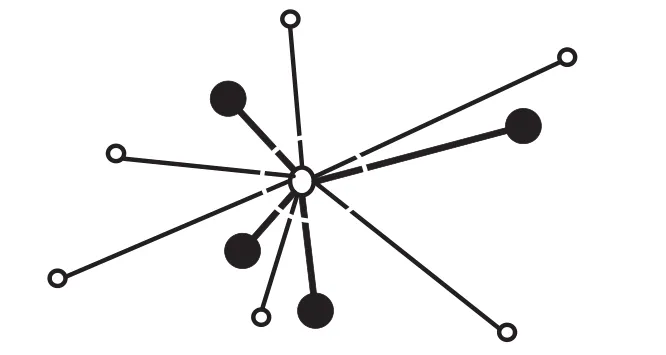
图1 x近邻点到x点的距离

设样本x的k近邻为N(x)。对任一x*∈N(x),D(x,x*)表示x*到x的距离（本文取Euclidean距离）。对标签yj来说，用Cj表示N(x)中样本对标签yj的加权值：

其中，若yj(x*)=1,x*具有yj标签；否则yj(x*)=-1。从式（3）可以看出，若x的k近邻中样本具有yj标签越多或者与x距离越近，则Cj(x)值就越大；反之，Cj(x)值就越小。与式（2）相比较，若D(x,x*)=1且标签取值为0，1时，即统计k近邻中样本的类别标签信息。由此，式（3）不仅考虑了具有标签类别的个数，而且考虑了样本间的距离，包含了原始数据集更多的信息。类似的，对表1的数据集，应用式（3）得到如表3的新数据集（保留小数点后4位），用C(x)=(C1(x),C2(x),…,Cq(x))表示样本x的新数据集下的属性特征向量，它是对原始数据集一种新的特征提取。同样的，在此数据集上建立回归模型，就可以进行多标签学习。

对于形如表3的回归模型，本文采取两种回归方法。第一种应用线性回归模型。通过属性的线性组合来进行分类的预测，对于yj标签的预测，通过yj上的输出：来确定，其中wj为与yj标签对应的q维列向量，bj为常数项。在此回归模型中新数据集的所有属性特征均考虑。对于测试样本x，若f(x,yj)＞0，则样本x具有yj标签，即yj(x)=+1；否则不具有yj标签，即yj(x)=-1。

为了获取权重wj和bj，针对每一标签yj，采用最小化误差平方和函数来得到，即对训练集：

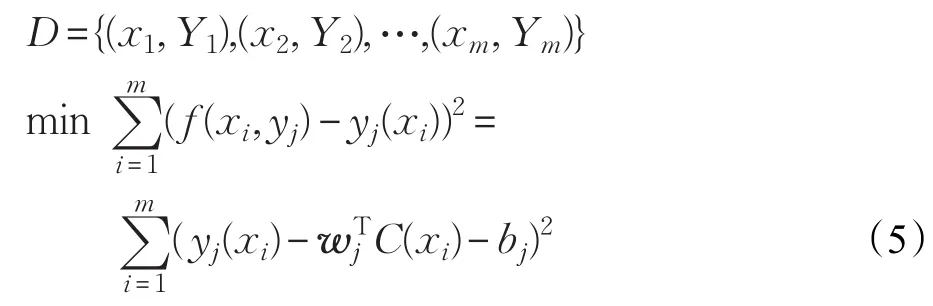
求解式（8），可得到线性回归系数ŵj，代入式（6），就可对测试样本进行分类。

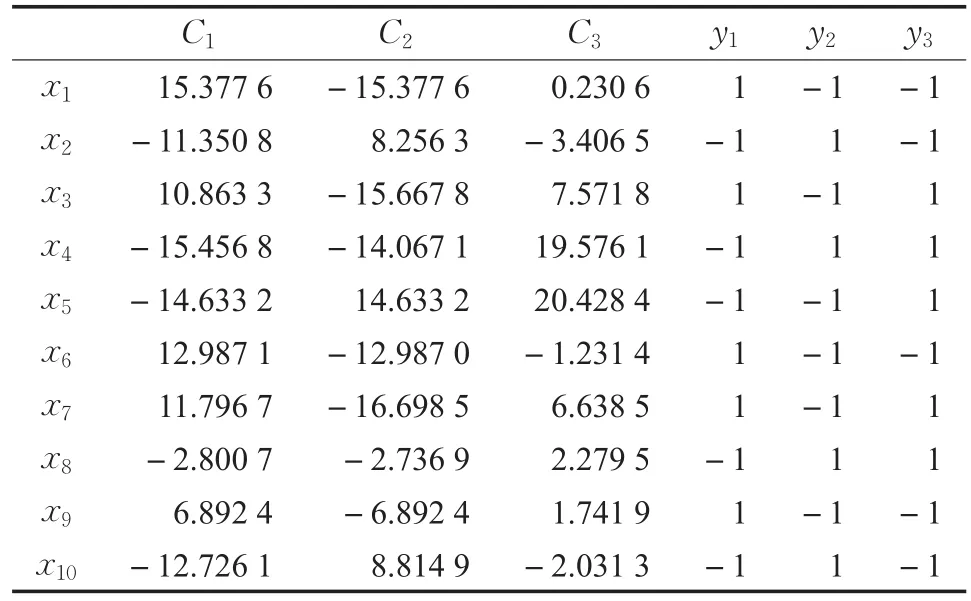
表3 考虑5近邻样本距离的新数据集

第二种方法采取Logistic回归。在线性回归中，选取新数据集的全部属性特征进行回归。在Logistic回归中，对yj标签，由于与Cj具有强相关性，仅取属性特征Cj对yj标签进行回归建模。由线性回归可以看出，对yj标签，仅考虑属性特征Cj，通过线性回归时产生实值。为了分类，需要将实值f转化为两个值，最理想的是单位阶跃函数。但其不连续，一般采用对数几率函数y=1/(1+e-f)来代替。对于yj标签的预测，通过yj上的输出

来确定，对于测试样本x，若f(x,yj)＞1/2，则x具有标签yj，即yj(x)=+1；若f(x,yj)≤1/2，则x不具有标签yj，即yj(x)=-1。

为了获取权重ŵj，一般采用极大似然法来估计ŵj。通过最小化

来得到。为了求解上式，可以通过牛顿法得到，其第t+1轮更新公式为：

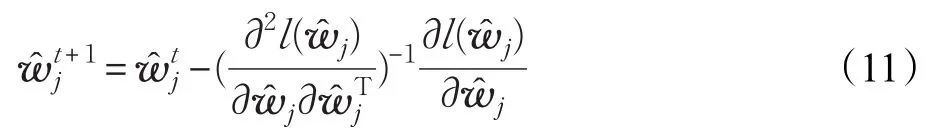
关于wj'的一阶、二阶导数分别为：

为此得到考虑k近邻样本距离的多标签学习算法，称之为回归多标签KNN算法（RML-KNN），用Lin-RML-KNN表示线性回归多标签KNN算法，用Log-RML-KNN表示Logistic回归多标签KNN算法。具体算法如下：

输入：数据集D={(x1,Y1),(x2,Y2),…,(xm,Ym)}；近邻个数k；测试样本x；

构造新的数据集

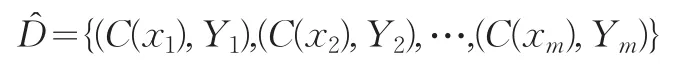
其中C(xi)=(C1(xi),C2(xi),…,Cq(xi))

通过式（1）计算样本x的k近邻N(x)；

计算输出f(x,yj)：线性回归通过式（6）计算；Logistic回归通过式（9）计算；

计算标签：对线性回归，若输出f(x,yj)＞0,则yj(x)=+1,否则yj(x)=-1；对Logistic回归，若输出f(x,yj)＞1/2,则yj(x)=+1,否则yj(x)=-1。

输出：测试样本的标签向量yj(x),f(x,yj),j=1,2,…,q。

在RML-KNN算法中，对于yj标签，通过新数据集Cj进行Logistic回归。为了更好地利用原始数据集的信息，可以添加原始数据x的属性特征进行回归。但由于属性特征个数一般较大，回归的维数过高，并不一定有好的效果。应用贝叶斯网理论，一个节点的Markov边界包括其父节点、子节点和子节点的父节点，节点的Markov边界与此节点具有强相关性，因此可以更好地包含原始数据集的信息。由此对于yj标签，除Cj外，添加yj标签关于原始数据集属性特征的Markov边界，在此基础上进行Logistic回归，称之为基于Markov边界的回归多标签KNN算法，记为MB-RML-KNN算法。对于Markov边界的计算，采取软件包来得到。其算法过程与RML-KNN类似，在此不再列出。

4 实验

本文实验的操作系统是Windows 7，Matlab 2015b。选取7个常用多标签数据集（见表4），取常用多标签学习算法BR[11]、Rank-SVM[16]、ECC[18]、ML-KNN[14]、IMLLA[15]，与本文提出的Lin-RML-KNN、Log-RML-KNN、MBRML-KNN算法进行比较，其中BR、ECC基分类器为SVM。各数据集每个标签的Markov边界通过Causal Explorer[20]软件包计算得到。

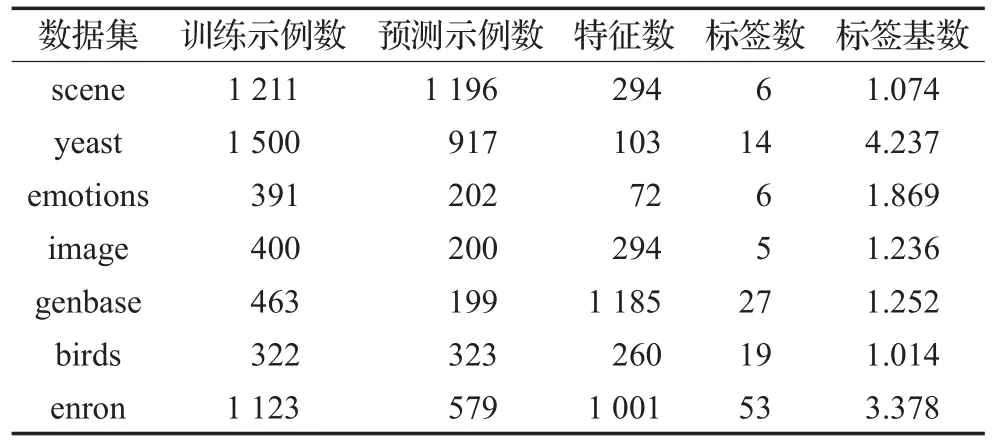
表4 实验数据集描述

已知多标签分类器h:X→2q以及多标签测试集T={(xi,Yi)|1≤i≤p}，其中Yi表示隶属于实例xi的相关标签集合，q表示标签个数，本文实验采用常用的5种多标签学习评价指标，定义如下：

对于任意的谓词π，当成立时π为1，否则π为0，该指标取值越小则算法越优。

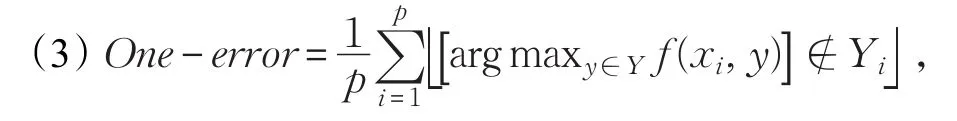
是与实值函数f(⋅,⋅)对应的排序函数，该指标取值越小则算法越优。

该指标取值越小则算法越优。

表5给出了各多标签学习算法在scene、emotions、yeast、image、genbase、birds、enron七个数据集上的实验结果。

由表5可以看出在scene数据集上，本文提出的算法Lin-RML-KNN、Log-RML-KNN、MB-RML-KNN在Hamming-loss上均优于其他5个算法，在提出的这三个算法中，MB-RML-KNN算法效果最好；在Ranking-loss、One-error、Coverage、Average-precision大多优于其他算法；但是这三个对ML-KNN改进的算法各项指标结果均优于ML-KNN，其中又属MB-RML-KNN算法效果最好。

在emotions数据集上，本文提出的算法Lin-RMLKNN、Log-RML-KNN、MB-RML-KNN在各项指标上效果不如BR、ECC，但都比ML-KNN、IMLLA效果要好，在这三个算法中又属MB-RML-KNN算法效果最好。

在yeast数据集上，本文提出的算法Lin-RMLKNN、Log-RML-KNN、MB-RML-KNN除在One-error上效果不如其余算法，但要比IMLLA要好，在Hammingloss、Ranking-loss、Coverage、Average-precision上均优于其他算法，在这三个算法中又属MB-RML-KNN算法效果最好。

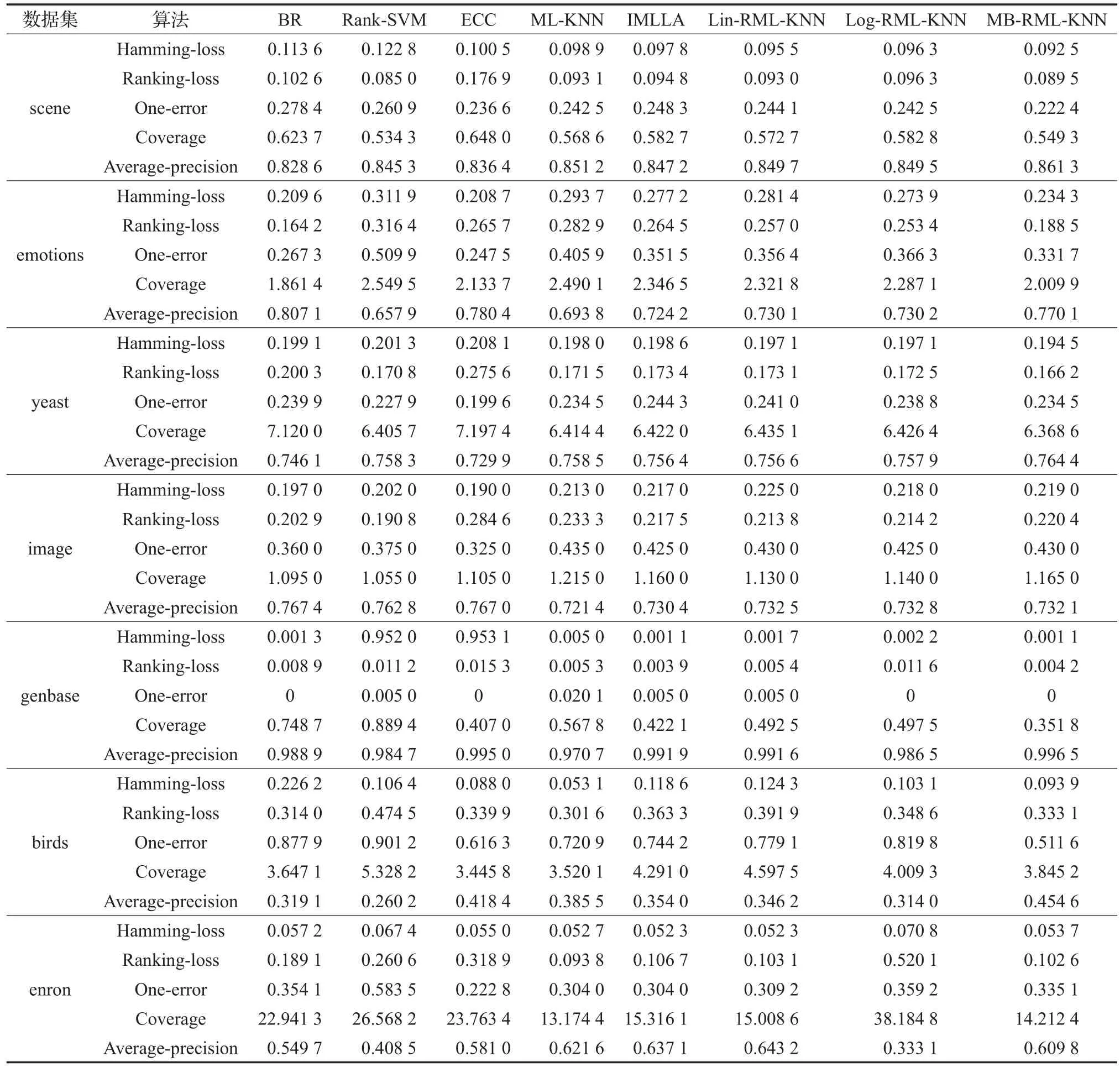
表5 不同算法在不同数据集上的对比结果

在image数据集上，本文提出的算法Lin-RMLKNN、Log-RML-KNN、MB-RML-KNN在各项指标上效果大多不如其他算法。

在genbase数据集上，本文提出的Lin-RML-KNN、Log-RML-KNN算法在各项指标上大多优于其他算法，MB-RML-KNN算法在各项指标上均优于其他算法。

在birds数据集上，本文提出的算法Lin-RMLKNN、Log-RML-KNN在各项指标上大多不如其他算法，MB-RML-KNN算法在各项指标上大多优于其他算法。

在enron数据集上，本文提出的算法Log-RMLKNN在各项指标上大多不如其他算法，Lin-RMLKNN、MB-RML-KNN算法在各项指标上大多优于其他算法。

下面是当邻域个数变化时，ML-KNN、IMLLA、Lin-RML-KNN、Log-RML-KNN、MB-RML-KNN五个算法在不同数据集上的指标变化情况。邻域个数k分别取3，6，9，…，30等10个值时的5个指标的取值，从而可以体现k值选取对于不同算法的影响。限于篇幅，选取scene、emotions、yeast和birds四个数据集，各指标变化情况分别如图2～图5所示。

图2 scene数据集各指标值的变化图

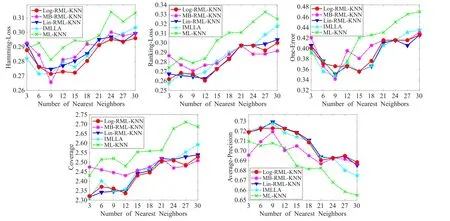
图3 emotions数据集各指标值的变化图

由图2可以看出在scene数据集上MB-RML-KNN算法在各指标上效果最好，而且当近邻个数取12时，MB-RML-KNN算法效果最佳。由图3可以看出在emotions数据集上MB-RML-KNN算法在各指标上效果最好，而且当近邻个数取6时，MB-RML-KNN算法的Hamming-Loss值效果最佳；当近邻个数取9时，MBRML-KNN算法的Ranking-Loss、Coverage、Average-Precision值效果最佳；当近邻个数取27时，MB-RMLKNN算法的One-Error值效果最佳。图4可以看出在yeast数据集上MB-RML-KNN算法在各指标上总体效果最好，而且当近邻个数取6时，MB-RML-KNN算法的Hamming-Loss、Ranking-Loss、Coverage值效果最佳；当近邻个数取9时，MB-RML-KNN算法的One-Error、Average-Precision值效果最佳。由图5可以看出在birds数据集上MB-RML-KNN算法One-Error、Average-Precision指标上效果很好，在其余指标上较IMLLA算法更好，比ML-KNN算法要差些。

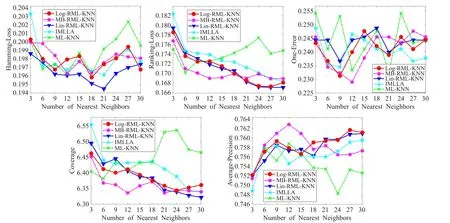
图4 yeast数据集各指标值的变化图

图5 birds数据集各指标值的变化图

5 结论

本文针对张敏灵提出的ML-KNN算法中未考虑近邻距离对标签的影响，考虑以样本与其近邻距离构造新的数据集，并利用线性回归与Logistic回归进行分类。但是上述构造新数据集的过程将原始数据集中信息丢失较多，为克服这种情况，考虑将标签的Markov边界加入到新数据集中，通过第4章的实验也充分说明此种方法的有效性。Markov边界选取了影响标签的主要属性特征，接下来将从理论上进行分析，并与其他特征选择算法进行对比分析。

[1] Mitchell T M.Machine learning[M].New York：McGraw-Hill，1997.

[2] Gao S，Wu W，Lee C H，et al.A MFoM learning approach to robust multiclass multi-label text categorization[C]//International Conference on Machine Learning.San Francisco：Morgan Kaufmann Publisher，2004：329-336.

[3] Li T，Ogihara M.Toward intelligent music information retrieval[J].IEEE Trans on Multimedia，2006，8（3）：564-574.

[4] Zhang M L，Zhou Z H.Multi-label neural networks with applications to functional genomics and text categorization[J].IEEE Trans on Knowledge and Data Engineering，2006，18（10）：1338-1351.

[5] Li P，Wu X，Hu X，et al.An incremental decision tree for mining multilabel data[J].Applied Artificial Intelligence，2015，29（10）：992-1014.

[6] Snoek C G M，Worring M，Van Gemert J C，et al.The challenge problem for automated detection of 101 semantic concepts in multimedia[C]//Proceedings of the 14th ACM International Conference on Multimedia，2006：421-430.

[7] Barutcuoglu Z，Schapire R E，Troyanskaya O G.Hierarchical multi-label prediction of gene function[J].Bioinformatics，2006，22（7）：830-836.

[8] Gopal S，Yang Y.Multilabel classification with meta-level features[C]//Proceedings of the 33rd International ACM SIGIR Conference on Research and Development in Information Retrieval，2010：315-322.

[9] Song Y，Zhang L，Giles C L.A sparse gaussian processes classification framework for fast tagsuggestions[C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management，2008：93-102.

[10] Madjarov G，Kocev D，Gjorgjevikj D，et al.An extensive experimental comparison of methods for multi-label learning[J].Pattern Recognition，2012，45（9）：3084-3104.

[11] Boutell M R，Luo J，Shen X，et al.Learning multi-label scene classification[J].Pattern Recognition，2004，37（9）：1757-1771.

[12] Fürnkranz J，Hüllermeier E，Loza Mencía E，et al.Multilabel classification via calibrated label ranking[J].Machine Learning，2008，73（2）：133-153.

[13] Tsoumakas G，Vlahavas I.Random k-labelsets：An ensemble method for multilabel classification[C]//Proceedings of ECML 2007，2007：406-417.

[14] Zhang M L，Zhou Z H.ML-kNN：A lazy learning approach to multilabel learning[J].Pattern Recognition，2007，40（7）：2038-2048.

[15] 张敏灵.一种新型多标记懒惰学习算法[J].计算机研究与发展，2012，49（11）：2271-2282.

[16] Cheng W，Hüllermeier E.Combining instance-based learning and logistic regression for multilabel classification[J].Machine Learning，2009，76（2/3）：211-225.

[17] Elisseeff A，Weston J.A kernel method for multi-labelled classification[C]//Advances in Neural Information Processing Systems，2002：681-687.

[18] Read J，Pfahringer B，Holmes G，et al.Classifier chains for multi-label classification[J].Machine Learning，2011，85（3）：333-359.

[19] Kocev D，Vens C，Struyf J，et al.Ensembles of multiobjective decision trees[C]//Proceedings of ECML 2007，2007：624-631.

[20] Aliferis C F，Tsamardinos I，Statnikov A R，et al.Causal explorer：A causal probabilistic network learning toolkitforbiomedicaldiscovery[C]//InternationalConference on Mathematics&Engineering Techniques in Medicine&Biological Sciences，2003，3：371-376.

QIAO Yaqin,MA Yingcang,CHEN Hong,et al.Multi-label classification algorithm of structure sample k-nearest neighbors data.Computer Engineering andApplications,2018,54（6）：135-142.

QIAO Yaqin,MAYingcang,CHEN Hong,YANG Xiaofei

School of Science,Xi’an Polytechnic University,Xi’an 710048,China

In multi-label classification,this paper constructs the new dataset about the nearest neighbors sample class mark through the classification idea of the k-nearest neighbors.The multi-label classification algorithm are established on the new dataset through the regression model.Firstly,this paper calculates the k-nearest neighbors distance of the test samples in each label and constructs new dataset of each sample on the label set.Secondly,the multi label classification algorithm is given based on sample k-nearest neighbors dataset,using linear regression and Logistic regression.In order to further exploit the information of original dataset,considering the Markov boundary of the original property each label and combining the feature of the new dataset to establish a new regression model,a multi-label classification algorithm about Markov boundary is proposed.The experimental results show that the multi-label learning method is better than the common learning algorithm.

multi-label classification;Logistic regression;k-nearest neighbors;Markov boundary

在多标签分类问题中，通过k近邻的分类思想，构造测试样本关于近邻样本类别标签的新数据，通过回归模型建立在新数据下的多标签分类算法。计算测试样本在每个标签上考虑距离的k近邻，构造出每个样本关于标签的新数据集。对新数据集采取线性回归和Logistic回归，给出基于样本k近邻数据的多标签分类算法。为了进一步利用原始数据的信息，考虑每个标签关于原始属性的Markov边界，结合新数据的特征建立新的回归模型，提出考虑Markov边界的多标签分类算法。实验结果表明所给出的方法性能优于常用的多标签学习算法。

多标签分类；Logistic回归；k近邻；Markov边界

2017-07-20

2017-10-16

1002-8331（2018）06-0135-08

A

TP18

10.3778/j.issn.1002-8331.1707-0337

国家自然科学基金（No.11501435）；西安市科技计划项目（No.CXY1441（2））；西安工程大学研究生创新基金（No.CX201726）。

乔亚琴（1992—），女，硕士研究生，研究领域为人工智能、多标签学习等；马盈仓（1972—），通讯作者，男，博士，教授，研究领域为机器学习、粒度计算等，E-mail：mayingcang@126.com；陈红（1992—），女，硕士研究生，研究领域为人工智能、多标签学习等；杨小飞（1982—），男，博士，副教授，研究领域为多值拓扑、多值图论及拟阵。