基于自适应变异算子的差分进化算法

廖雄鹰，李俊，罗阳坤，李波

1.武汉科技大学计算机科学与技术学院，武汉430065

2.智能信息处理与实时工业系统湖北省重点实验室，武汉430065

基于自适应变异算子的差分进化算法

廖雄鹰1，2，李俊1，2，罗阳坤1，2，李波1，2

1.武汉科技大学计算机科学与技术学院，武汉430065

2.智能信息处理与实时工业系统湖北省重点实验室，武汉430065

1 引言

差分进化算法[1]（Differential Evolution，DE）是一种简单而又有效的用于解决函数优化问题的智能算法，具有原理简单、控制参数少、鲁棒性强和易于实现等特点。从1995年被Storn和Price提出至今，已在多个工程领域得到了成功应用，例如化工[2]、人工神经网络[3]和机器人[4]等。

DE算法中提出了多种基本的变异策略，不同策略具有不同的性能。为适应更为复杂的优化问题和满足更高的求解质量，研究人员不断地挖掘不同策略的潜能，在基本变异策略的基础上设计和改进出了一些新颖的变异算子。Fan和Lampinen[5]提出了一种三角变异算子，该算子利用随机选择的三个个体中最好个体的信息，引导实验向量向其靠近；Price等[6]提出一种DE/rand/1/either-or算子，该算子将DE/rand/1和一个重组算子相混合，并通过参数来控制两个算子的选择；Das等[7]提出一种具有邻域搜索能力的DE/target-to-best/1变异算子，为平衡算法的勘探能力和开采能力，与原有DE/target-tobest/1变异算子进行混合，提出了DEGL算法；受粒子群优化算法启发，Zhang和Sanderson在JADE[8-9]中提出了一种DE/current-to-pbest/1算子，该算子不仅利用种群中最好个体的信息，还利用邻域中较好的个体的信息；Wu等[10]结合DE/rand/1/bin、DE/best/rand/1/bin勘探和开采的优势，提出一种自适应变异算子；Wang等[11]提出一种精英变异策略，该算法从种群中选择20%的个体作为精英个体指导算法的搜索，在勘探和开采中找到一个较好的平衡。张锦华等[12]为平衡全局勘探能力和局部搜索能力，提出一种加权变异策略动态差分进化算法。这些研究工作对变异策略进行了改进，在一定程度上提高了DE的性能。

然而DE及诸多变种仍然存在收敛速度慢和易陷入局部最优等问题，特别是在进化后期，DE的种群多样性降低，收敛速度下降，很容易导致算法陷入局部最优。为保持DE的种群多样性，避免早熟，加快收敛速度，本文提出一种基于自适应变异算子的差分进化算法（A differential evolution algorithm based on adaptive mutation operator，AMODE）。算法提出一种基于种群聚集度自适应的变异算子，它依据种群个体的聚集度自适应地调整DE/best/1变异算子和加权异维学习变异算子的变异权重：在种群个体分散时，DE/best/1变异算子的权重占优，保证算法的收敛速度；随着种群个体之间的差异性变小，种群愈发聚集时，加权异维学习变异算子的权重增大，从而可以有效增强种群的多样性，避免算法陷入局部最优，进一步加快算法收敛速度，提高算法的求解精度。通过对20个典型的测试函数的实验结果表明，与其他7种具有代表性的算法相比，本文提出的算法在收敛速度和求解精度上有很大提高。

2 差分进化算法

差分进化算法（DE）主要操作有群体初始化、变异操作、交叉操作、选择操作等。其主要思想是将同一群体中两个互不相同的个体向量进行差分以及缩放，并与该群体中的第三个个体向量相加得到一个变异个体向量，然后变异个体向量与父代个体向量以一定概率进行杂交生成尝试个体向量；最后，将尝试个体向量与父代个体向量进行贪婪选择，较优个体向量被保存到下一代群体当中。

其中，变异操作是DE产生后代个体的主要方式，它通过差分变换来产生新的变异个体，这种生成变异个体的方式即称为变异算子。常见的变异算子如下所示：

其中F∈[0,1]为缩放因子，i,r1,r2,r3,r4,r5为[1,NP]上的随机整数，且互不相等。各个算子各有其优劣：其中，“rand”变异方式的DE算法能有效保持整个种群的多样性，从而具有良好的全局探索能力，但也存在收敛速度慢的问题；基于“best”变异方式的DE进化模式，以当前种群中适应度最好的个体作为基矢量，具有良好的局部开发能力和快速收敛的特性，但很容易陷入局部最优点而导致早熟。

3 AMODE算法

为了更好描述AMODE算法，本文特提出了个体向量粒子、维度层、种群聚集度等定义。

定义1个体向量粒子。对于群体P中的第i个个体，令个体的个体维度为D，记为：

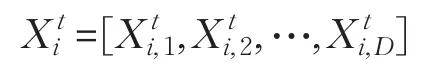
定义2维度层。如图1所示，一层代表一个维度，表示群体P的所有个体在这一维度上的个体向量粒子的集合，将这个集合定义为一个维度层。

图1 种群的维度层示意图

由公式（1）～（3）可知，在传统的差分进化算法中，对于一个变异向量而言，它在第j维上的个体向量粒子均来源于这一维度，即变异向量的个体向量粒子的变异来源维度层固定，则对于一个单独的维度层而言，它的变异、交叉、选择操作是独立的、与其他维度层无关的，即各个维度层的进化过程是独立且无关联的。

定义3种群聚集度。设群体规模为NP，D表示群体个体的纬度，为种群在第k维度层上的个体向量粒子的平均值，Xik为个体Xi在第k维上的个体向量粒子，则种群聚集度C可以定义为：

定义3表明，种群聚集度C体现了种群个体的聚集程度：C越小，说明种群个体的差异性越小，聚集程度就越高；反之，说明种群个体分散，种群多样性良好。因而，种群聚集度C可以很好地描述种群个体的聚集程度。

种群聚集度C越大，种群的多样性就越差，算法就越容易陷入局部最优，从而导致早熟。

3.1 加权异维学习

定义4异维学习（Different Dimensional Learning，DDL）[13-14]。在种群P的维度层中随机选出第j,m维两个维度层且m≠j，则异维学习定义为：

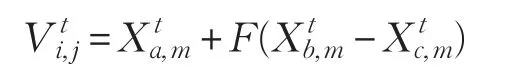
其中，i,a,b,c为[1,NP]上的随机整数，且互不相等。个体在第j维维度层上的个体向量粒子变异来源于第m维维度层，因而被称为异维学习。

异维学习概念由李冰等[13]在异维学习人工蜂群算法中被提出，因其搜索具有跳跃性的特点，可以很好地提高观察蜂群跳出局部最优的概率。鉴于异维学习的优点，本文创新性地将异维学习策略引入差分演化算法中。

在差分演化算法中引入异维学习策略的依据为：若群体某一维度层或者某几个维度层由于个体向量粒子聚集程度很高而使算法陷入局部最优，则单靠它自身维度层的探索开发很难或者不能跳出当前状态。而对整个种群，其各个维度层的进化过程是独立且无关联的，这时就可以借助其他维度层上的优秀个体向量粒子对本维度层进行跳跃式地搜索，进而跳出早熟状态。这样就可以减少算法陷入局部最优的概率，加快算法的收敛速度。

但对于上述异维学习而言，它的异维维度m的选取是完全随机的，这种不同维度层之间的随机的异维学习具有很大盲目性和不确定性，可能导致算法早熟、收敛速度受到限制。为此，本文提出一种基于维度层加权的异维维度选择策略：设Qk(k∈[1,D])为第k个维度层在第g代进化时被选择参与变异的概率权重，初始值为1/D，更新公式如下：

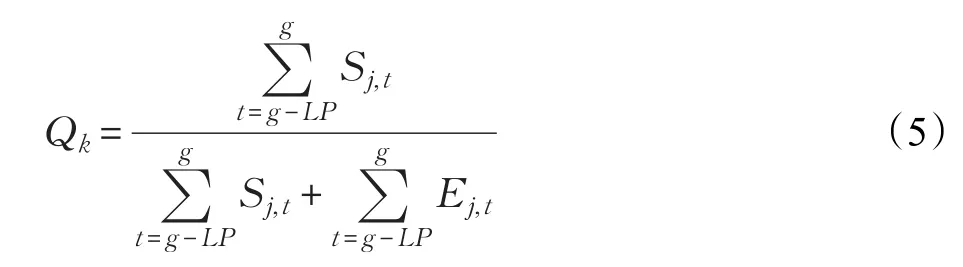
其中，g(g＞LP)为当前进化的代数（为保证进化信息统计的最新性和有效性，选择最新的LP代作为样本）。Sj,t为第j个维度层在第t代进化中参与变异且成功进入下一代群体的数目，而Ej,t为第j个维度层在第t代进化中参与变异但进入下一代群体失败的数目。进化时，对各维度层的概率权重Qk(k∈[1,D])采取随机广义选择的方式确定变异的异维维度K。基于这一异维维度选择策略，提出一种加权异维学习变异算子：

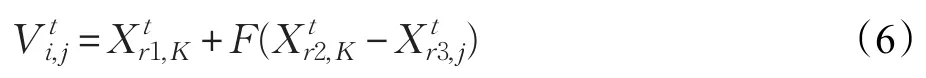
其中i,r1,r2,r3为[1,NP]上的随机整数，且互不相等；j,K∈[1,D]表示个体的维度，其中K是由公式（5）的Qk(k∈[1,D])采用随机广义选择方式确定变异的异维维度。此变异算子的基矢量来源于不同于j维的其他维度层，可以引进其他维度层的优秀个体向量粒子对当前维度层进行跳跃式的优化搜索。

3.2 基于种群聚集度自适应的变异算子

DE变异策略有多种不同的变化形式，每一种变化形式都有其自身的特点，对算法的侧重点也不一样，有的强调全局搜索能力，而有的强调收敛速度。如：基于“best”变异方式的DE算法，以当前种群中适应度最好的个体作为基矢量，具有良好的局部开发能力和加快收敛特性，但很容易陷入局部最优而导致早熟。

产生早熟的根本原因是随着迭代次数的增加，个体之间的差异性减小，种群多样性下降。为解决种群多样性下降的问题，本文在“best”变异的基础上引入加权异维变异的策略，依据种群聚集度（种群多样性）自适应地调整DE/best/1变异算子和加权异维学习变异算子的变异权重：在进化的前期，种群个体分散，多样性良好时，让DE/best/1变异算子的权重占优，能充分地发挥DE/best/1变异策略快速收敛的特性；而随着进化的不断推进，种群个体之间的差异性变小，种群聚集愈发明显，种群多样性降低时，就要加大加权异维学习变异算子的变异权重，增加种群的多样性，保证算法的收敛性能。由前面分析可知，各个维度层的进化过程是独立且无关联的，所以各维度层的个体向量粒子在进化后期仍然具有良好的差异性，这样就可以借助其他维度层上的优秀个体向量粒子对本维度层进行跳跃式地搜索，从而增加种群的多样性，避免早熟，同时也能保证算法的收敛速度和解的精度。

本文结合DE/best/1和加权异维学习两种变异算子，综合两者的优势，提出一种基于种群聚集度自适应的变异算子：

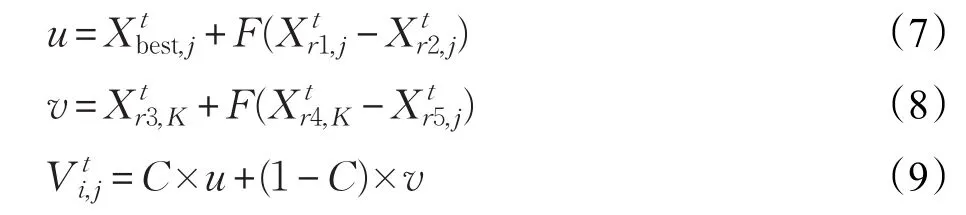
其中F∈[0,1]为缩放因子，i,r1,r2,r3,r4,r5为[1,NP]上的随机整数，且互不相等；j,K∈[1,D]且K≠j表示个体的维度，K是对公式（5）中的Qk(k∈[1,D])采用随机广义选择方式确定的变异的异维维度。C为种群聚集度，代表种群当前的聚集程度，当C∉[0.05,0.95]时，将C截断到[0.05,0.95]的区间内。

这种基于种群聚集度自适应的变异策略在保证快速收敛的同时，又能很好地解决因种群多样性下降算法陷入局部最优而导致的早熟问题，大大提高了DE的收敛性能。

3.3 AMODE算法步骤

AMODE算法具体实现步骤如下：

（1）产生初始化群体X0

（2）评价群体X0中所有个体的适应值，并选出最优适应值个体Xtbest

（3）初始化种群聚集度C和群体各维度层的概率权重Qk

（4）While未满足终止条件do

（5）

（6）随机均匀选择r1≠r2≠r3≠r4≠r5≠i

（7）随机产生整数jrand∈[1,D]

（8）由Qk采用随机广义选择方式确定变异的异维维度K

（21）依据式（4）计算种群Xt当前的种群聚集度C

（22）根据式（5）调整群体各维度层的概率权重Qk

（23）end while

3.4 算法流程图

AMODE算法流程图，如图2所示。

3.5 算法复杂度分析

根据3.4节中AMODE算法步骤分析其时间复杂度，设其中种群规模为NP，问题维度为D，迭代次数为T。第（1）～（3）步群体初始化，第（2）步适应度函数评价和第（3）步参数初始化操作均为O(NP×D)。

第（10）步变异和交叉操作为O(D)，则第（5）～（12）步每一次迭代计算为O(NP×D)。第（13）～（19）步的选择操作、第（20）步的最优个体选择操作、第（21）步的种群聚集度更新操作和第（22）步的群体各维度层的概率权重调整均为O(NP×D)。则（4）～（22）步总的时间复杂度为O(T×NP×D)。

综上所述，AMODE算法总的时间复杂度为O(T×NP×D)，仅与T、NP和D有关。AMODE算法与标准DE算法的时间复杂度一致，对算法的改进没有增加过多的开销。

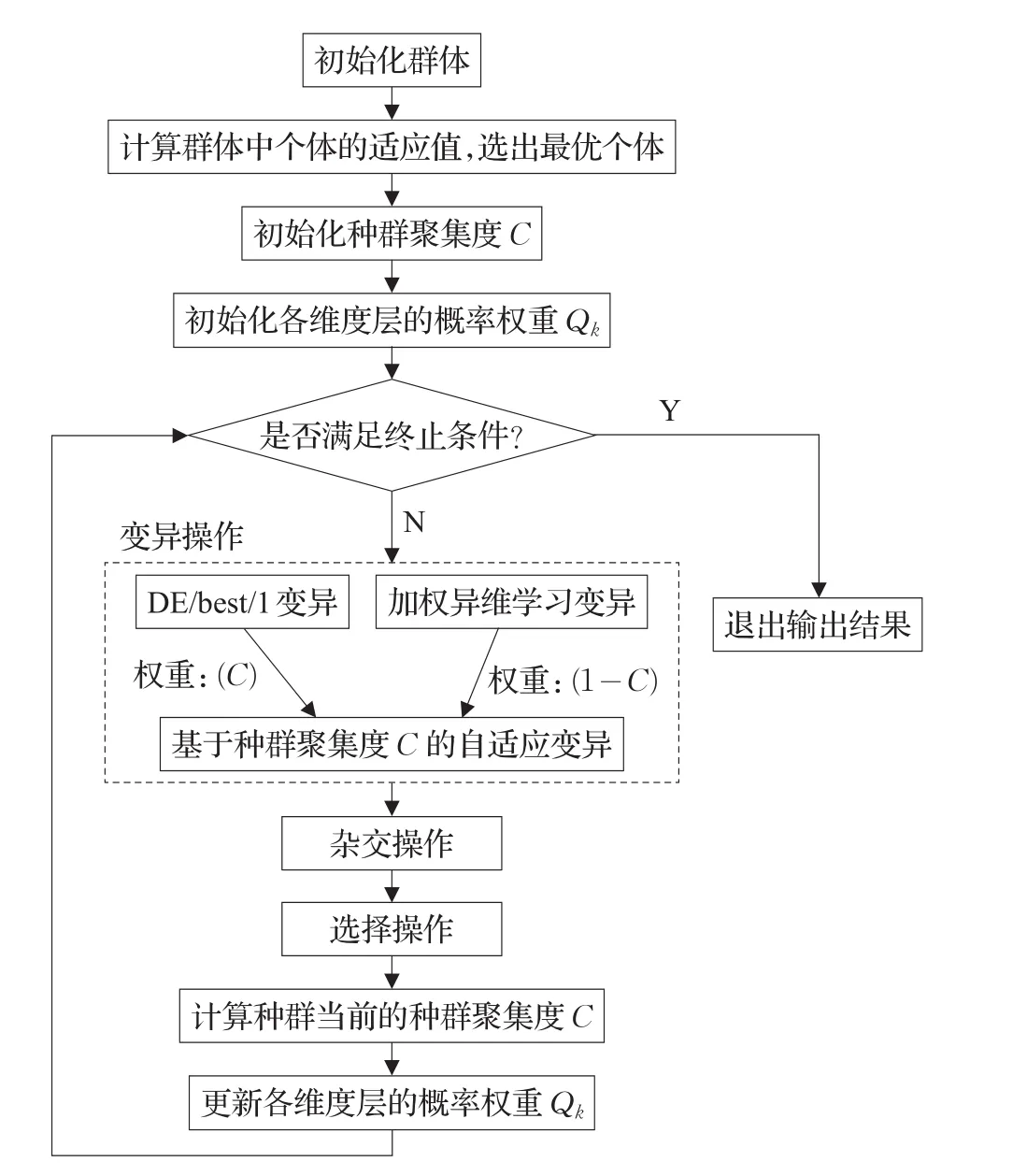
图2 AMODE算法流程图

4 实验仿真及分析

4.1 测试函数

为验证AMODE算法的高效性和鲁棒性，选择在20个典型的测试函数[15-16]上进行实验，其中，f1～f7为单模态函数；f8～f13为多模态函数；f14～f20为偏移函数[16]。对所有的测试函数分别选取维数D=30和D=100进行仿真实验，测试函数的具体相关信息如表1所示。

实验中的算法由MATLAB语言实现，软件为MATLAB 2012b。运行环境为：Windows 7、双核3.2 GHz CPU、4 GB内存。

4.2 参数设置

为验证AMODE算法性能，选取了DE/best/1、DE/current-to-best/1、DE/rand/1/either-or[6]、DEGL[8]、JADE[9，17]等变异策略的进化算法，以及与基本粒子群算法PSO[18]、基本遗传算法GA[19]等经典算法作比较，对测试函数进行寻优仿真。

AMODE算法参数设置为缩放因子F=0.5，交叉概率Cr=0.9。为了比较的公平，种群规模NP均为40，最大进化代数为5 000代，文中涉及“best”变异策略的算法参数设置为：缩放因子F=0.5，交叉概率Cr=0.9；使用“rand”变异策略的算法参数设置为：缩放因子F=0.5，交叉概率Cr=0.1；PSO算法加速因子设置为c1=c2=2，其惯性权重w=0.712；GA算法交叉概率设置为0.5，交叉概率为0.1；其他参数与其参考文献中的保持一致。为消除在运行过程中随机因素的影响，每个测试函数独立运行30次。

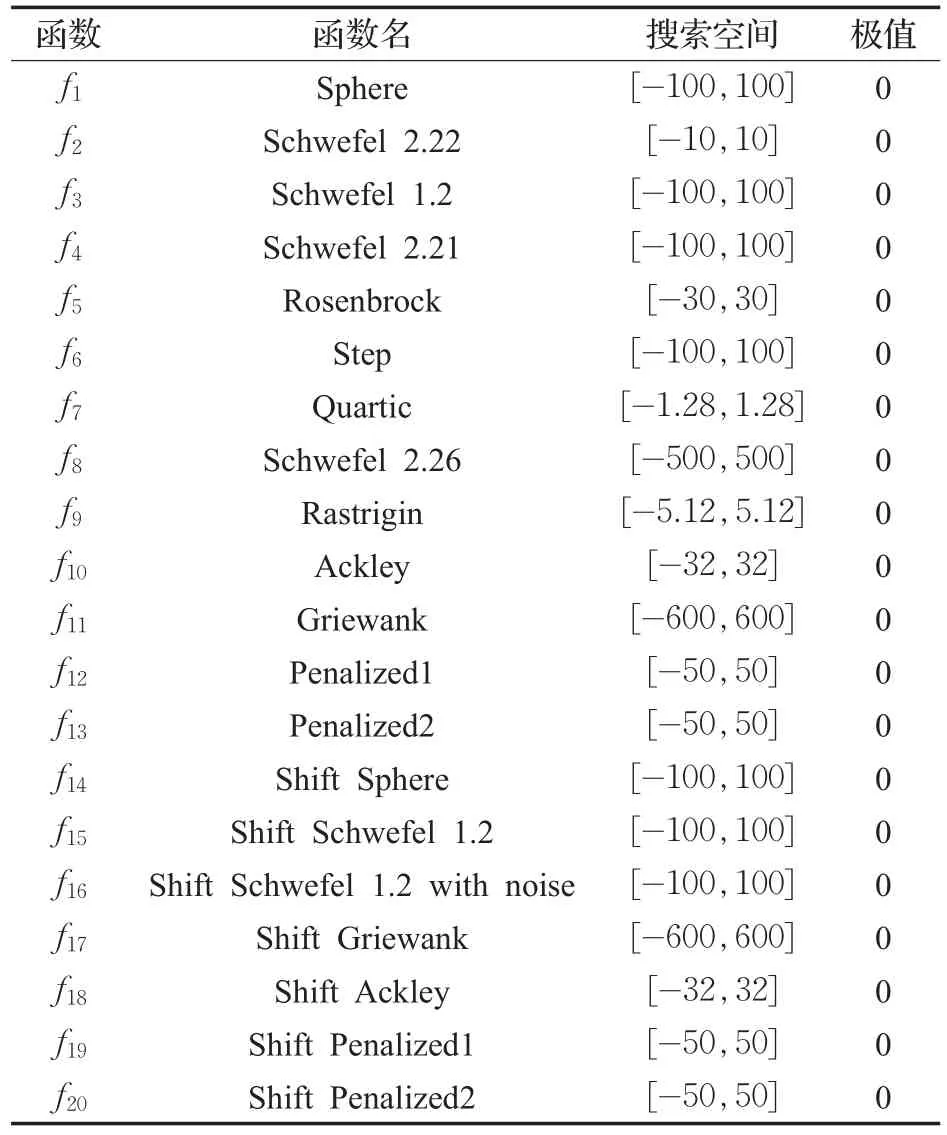
表120 个典型测试函数

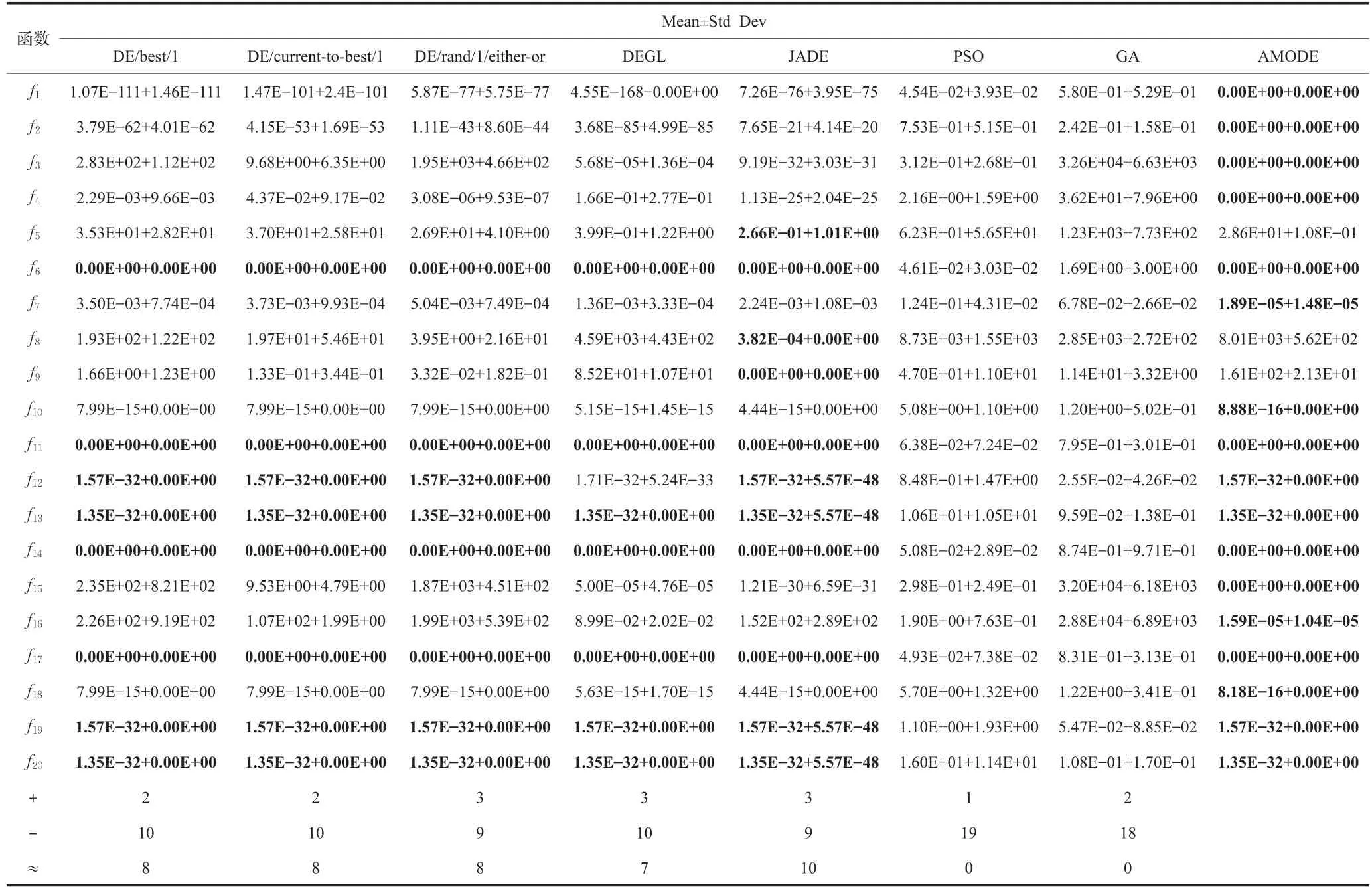
表2 D=30时AMODE算法与其他算法的实验结果及统计

4.3 实验结果及分析

实验分为两组，一组的测试函数为D=30；另一组的测试函数为D=100。实验记录各个算法运行得到的最优适应度值的平均值（Mean）与标准差（Std Dev），表2为函数为30维的实验结果，表3为函数为100维时的测试结果。为客观地评价AMODE算法与对比算法在测试函数上的性能差异程度，采用Wilcoxon秩和检验方法对实验结果进行了统计分析，其中“+”、“-”、“≈”分别表示对比算法的性能要优于、劣于、相当于AMODE算法。

当D=30时，从表2最后三行可以看出，AMODE算法在大部分函数上的求解精度要优于其他几种算法，且在15个函数上的求解标准差均为0，稳定性要远远高于其他算法。相比于DE/best/1、DE/current-to-best/1和DEGL算法，AMODE算法在10个函数上求解的精度更优；相比于DE/rand/1/either-or和JADE算法，AMODE算法在9个函数上求解的精度更优；较之PSO算法和GA算法，AMODE分别在19个、18个函数上求解的精度更优。虽然在函数f5、f8和f9上，AMODE算法取得的效果一般，但在大部分函数上都取得了极好的最优值，在一些函数上收敛到了全局最优值。且AMODE算法求解稳定性最好，在15个函数上的求解标准差均为0，占总测试函数的75%，高于DE/best/1算法的50%和JADE算法的40%。

当D=100时，各算法的实验结果如表3所示，从中可以看出随着维数的增加，DE/best/1、DE/current-tobest/1、DE/rand/1/either-or、DEGL、JADE等算法的性能均大幅度下降，但是同比于D=30时，AMODE算法仍保持良好的收敛性能，甚至在个别函数如f12、f19上有了小幅度的提高，收敛性能受维度的影响很小，具有非常好的鲁棒性。AMODE算法在大部分函数上的求解精度要远远优于其他几种算法，从表3的最后三行可以看出，AMODE算法的求解精度在18个函数上比DE/best/1、DE/current-to-best/1、DE/rand/1/either-or、DEGL算法和GA算法更优，在17个函数上比JADE算法更优，在19个函数上较之PSO算法更优。在其他算法收敛精度大幅度下降的情况下，AMODE算法在大部分函数上仍然取得了极好的最优值，并且AMODE算法仍然在14个函数上的求解标准差为0，稳定性要远远高于其他算法。

从表2和表3可以看出，无论是D=30或D=100时，在大部分函数上，AMODE算法的收敛精度以及稳定性较之其他算法更优。

为了进一步研究AMODE算法在不同函数上的收敛速度，特意选取一个较高的维度(D=100)时，在20个测试函数上进行实验。实验结果表明：在其他算法的收敛速度受到高纬度的限制时，AMODE算法在大多数函数上的收敛速度较之其他算法更快，仍具有较高的收敛性能。图3给出了D=100时各算法在测试函数上的收敛曲线，其中lg表示以10为底色的对数（限于篇幅，只给出具有代表性的6个函数）。

从图3可以看出，在Sphere函数上，AMODE算法的收敛速度要显著地快于其他对比算法；而对于Quartic函数而言，因其是一个带噪声的函数，求解比较困难，但从图3的求解图像可以看出，AMODE算法对减轻噪声有效果，且收敛速度更快；在Ackley函数上，虽然AMODE算法在求解精度上的改进相对较小，但表现出了更快的收敛速度；在偏移函数f15上，AMODE算法表现出了极快的收敛速度；f15加上噪声因素时即变f16为偏移函数，在函数f16上的收敛曲线再次表明AMODE算法具有消除噪声效果，且收敛速度更快。AMODE算法在多数测试函数上都取得了良好的收敛速度，效果显著，然而，对于一些具有特殊性质的测试函数来说，比如f8（Schwefel 2.26）和f9（Rastrigin），它们的适应度函数地貌非常具有欺骗性，在搜索范围内存在非常多的局部最小值点，且全局最优点所处位置特殊，使得AMODE算法效果一般。

表3 D=100时AMODE算法与其他算法的实验结果及统计

综上以上实验分析可以发现，虽然AMODE算法在极少数函数上的性能不佳，但对于绝大多数函数而言，基于种群聚集度自适应的变异策略较大地提高了DE算法的收敛速度和收敛精度，同其他7种对比算法相比，AMODE算法的优化性能仍具有很大的优势，且稳定性更佳。

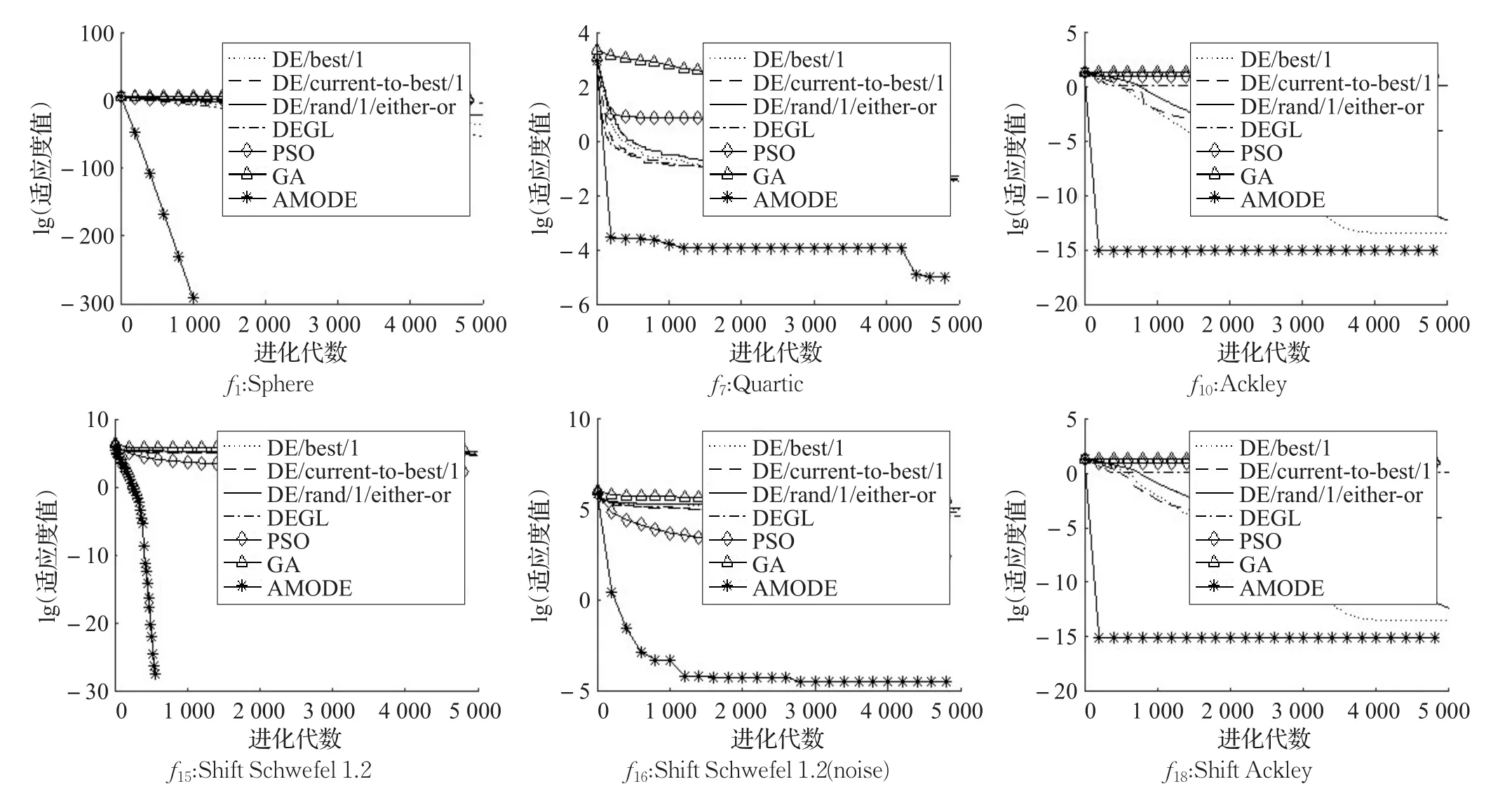
图3 D=100时各算法的收敛曲线

5 结语

为保持DE的种群多样性，避免早熟，加快收敛速度，本文算法提出一种基于种群聚集度自适应的变异算子，该算子依据种群个体当前的的种群聚集度自适应地调整DE/best/1算子和加权异维学习变异算子的变异权重，充分发挥DE/best/1算子快速收敛和加权异维学习变异算子增强种群的多样性、避免算法陷入局部最优的特点。通过一系列对比实验表明，本文提出的算法在求解精度和收敛速度上取得了很大进步，且具有良好的稳定性。但也在个别函数，如f8、f9上性能不佳，针对这些特殊函数，如何进一步提高它们的性能，需要进行更加深入的研究。

[1] Storn R，Price K.Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

[2] Liu C，Song X，Xu T，et al.An operation optimization method based on improved EDA for BOF end-point control[C]//IEEE Congress on Evolutionary Computation，2016：1077-1084.

[3] Leema N，Nehemiah H K，Kannan A.Neural network classifier optimization using differential evolution with global information and back propagation algorithm for clinical datasets[J].Applied Soft Computing，2016，49：834-844.

[4] Jiang L，Qiu H，Wu Z，et al.Active disturbance rejection control based on adaptive differential evolution for twowheeled self-balancing robot[C]//Chinese Control and Decision Conference，2016.

[5] Fan H Y，Lampinen J.A trigonometric mutation operation to differential evolution[J].Journal of Global Optimization，2003，27（1）：105-129.

[6] Price K，Storn R，Lampinen J.Differential evolution：A practical approach for global optimization[M].Berlin：Springer Verlag，2005.

[7] Das S，Abraham A，Chakraborty U K，et al.Differential evolution using a neighborhood-based mutation operator[J].IEEE Transactions on Evolutionary Computation，2009，13（3）：526-553.

[8] Zhang J，Sanderson A C.JADE：Adaptive differential evolutionwithoptionalexternalarchive[J].IEEETransactions on Evolutionary Computation，2009，13（5）：945-958.

[9] Zhang J，Sanderson A C.JADE：Self-adaptive differential evolutionwithfastandreliableconvergenceperformance[J].Soft Computing，2011，15（8）：1581-1599.

[10] Wu Lianghong，Wang Yaonan，Yuan Xiaofang.Design of 2-D recursive filters using self-adaptive mutation differentialevolutionalgorithm[J].InternationalJournal of Computational Intelligence Systems，2012，4（4）：644-654.

[11] Wang S W，Duan Y M，Shu W N，et al.Differential evolution with elite mutation strategy[J].Journal of Computational Information Systems，2013，9（3）：855-862.

[12] 张锦华，宋来锁，张元华，等.加权变异策略动态差分进化算法[J].计算机工程与应用，2017，53（4）：156-162.

[13] 李冰，孙辉，赵嘉，等.异维学习人工蜂群算法[J].计算机应用研究，2016，33（4）：1028-1033.

[14] Banharnsakun A，Achalakul T，Sirinaovakul B.The bestso-far selection in artificial bee colony algorithm[J].Applied Soft Computing，2011，11（2）：2888-2901.

[15] Yao Xin，Liu Yong，Lin Guangming.Evolutionary programming made faster[J].IEEE Transactions on Evolutionary Computation，1999，3（2）：82-102.

[16] Wang H，Wu Z，Liu Y，et al.Space transformation search：A newevolutionarytechnique[C]//Proceedingsofthe First ACM/SIGEVO Summit on Genetic and Evolutionary Computation，Shanghai，China，June 2009：537-544.

[17] 周新宇，吴志健，王晖.一种精英反向学习的差分演化算法[J].小型微型计算机系统，2013，34（9）：1647-1652.

[18] Jong K A D.Analysis of the behavior of a class of genetic adaptive systems[D].University of Michigan，1975.

[19] Kennedy J.Particle swarm optimization[M]//Encyclopedia of Machine Learning.US：Springer，2010：760-766.

LIAO Xiongying,LI Jun,LUO Yangkun,et al.Differential evolution algorithm based on adaptive mutation operator.Computer Engineering andApplications,2018,54（6）：128-134.

LIAO Xiongying1，2,LI Jun1，2,LUO Yangkun1，2,LI Bo1，2

1.College of Computer Science and Technology,Wuhan University of Science and Technology,Wuhan 430065,China
2.Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System,Wuhan 430065,China

In order to solve the problem of differential evolution algorithm,such as premature convergence,slow convergence speed and low convergence precision,a differential evolution algorithm based on adaptive mutation operator is proposed.In this paper,the definition of individual vector particle and dimensional layer is presented.Based on the different dimension’s selection strategy for weighted dimensional layer,the weighted different dimensional learning is introduced into differential evolution algorithm for the first time,which can effectively improve the diversity of the population.According to the degree of populational aggregation,and an adaptive mutation operator based on degree of populational aggregation is proposed.The operator can adaptively adjust the variation weight of DE/best/1 mutation operator and the different dimensional learning mutation operator according to the degree of populational aggregation currently.It accelerates the convergence speed,improves the convergence precision of the algorithm.20 typical test functions are tested,the results show that compared with the 7 representative algorithms,the algorithm proposed in this paper has great advantages in solving accuracy and convergence speed,and it shows very good robustness.

differential evolution;dimensional layer;weighted different dimensional learning;degree of populational aggregation;adaptive mutation operator

针对差分演化算法易于早熟、收敛速度慢和收敛精度低等问题，提出一种基于自适应变异算子的差分进化算法。给出个体向量粒子及维度层定义，并提出了基于维度层加权的异维维度选择策略，首次将加权异维学习策略引入差分演化算法中，有效地提高了种群的多样性；根据种群聚集度的思想，提出一种基于种群聚集度自适应的变异算子，该算子能依据种群个体当前的种群聚集度自适应地调整DE/best/1变异算子和加权异维学习变异算子的变异权重，加快算法收敛速度、提高其收敛精度。通过在20个典型的测试函数上进行测试，与7种具有代表性的算法相比，结果表明提出的算法在求解精度和收敛速度上具有很大优势，并显示出了非常好的鲁棒性。

差分进化；维度层；加权异维学习；种群聚集度；自适应变异

2017-09-04

2017-10-27

1002-8331（2018）06-0128-07

A

TP301.6

10.3778/j.issn.1002-8331.1709-0023

国家自然科学基金（No.61572381）。

廖雄鹰（1991—），男，硕士研究生，主要研究方向：智能计算；李俊（1978—），男，博士，副教授，主要研究方向：智能计算，E-mail：250581376@qq.com；罗阳坤（1992—），男，硕士研究生，主要研究方向：智能计算；李波（1975—），男，博士，教授，主要研究方向：智能计算、机器学习。