基于亲和度的引力移动算法

赵蕊娟，杨连贺

天津工业大学计算机科学与软件学院，天津300387

基于亲和度的引力移动算法

赵蕊娟，杨连贺

天津工业大学计算机科学与软件学院，天津300387

CNKI网络出版：2017-03-13,http://kns.cnki.net/kcms/detail/11.2127.TP.20170313.1638.024.html

1 概述

近年来，许多相关研究人员通过观察自然界中各种自然现象并从中受到了启发，提出了很多启发式优化算法来解决一些复杂的问题，例如：中心力算法[1]、模拟退火算法[2]、蚁群算法[3]、遗传算法[4]、粒子群算法[5]等。这些启发式优化算法只在某些特定问题上提供了有效解决问题的途径，在解决一些高维空间优化问题时存在着搜索解的精度较低、搜索解过程中容易陷入局优导致算法收敛速度慢等问题。因此，探索新的算法仍然是必要的。

引力搜索算法（Gravitational Search Algorithm，GSA）是近年来伊朗克曼大学的教授EsmatRashedi等[6-7]提出的基于牛顿第二定律和万有引力定律的一种新型启发式优化算法。目前有关引力搜索算法的研究已经陆续展开，在应用方面，文献[8]将GSA用于解决流水线调度问题时获得了较好的效果，文献[9-10]将模糊C-mean算法与GSA相结合用于求解模糊聚类问题，文献[11]将GSA应用到船舶船舱的布置上得出的方案能较好地符合算例的要求，文献[12]用GSA求解该电力系统电压无功控制的数学模型；在理论研究方面，文献[13-14]从不同的角度对算法进行了改进以增强其优化性能。在GSA算法的基础上文献[15]提出了一种新型的群体搜索优化算法引力移动算法（GMA）并在文中证明了GMA的搜索解的精度和稳定性明显优于粒子群算法。但是引力移动算法在使用中仍然存在着过早陷入局部最优解导致收敛速度过早，搜索精度相对较低问题。本文针对这种群体搜索算法GMA的不足，引入亲和度概念，对GMA算法中合力公式加以改进，使个体能够更快地向最优方向移动，并通过试验验证改进方法的有效性。

2 引力移动算法（GMA）

2.1 算法思想

在引力移动算法中，个体在解空间中位置的优劣用个体质量大小来表示，初始状态下种群中个体随机分布在可行域中。种群中的每个个体均受万有引力作用，在其作用下质量小的个体会逐渐向质量大的个体移动，种群整体呈现出收敛态势，最终整个种群收敛到一点，该点即为种群最优解。

假定有一个种群的规模为N的D维目标搜索空间，则种群中第i个个体的位置向量定义为：

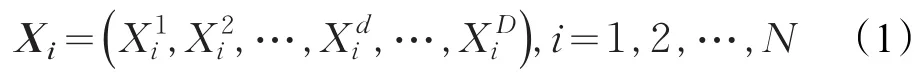
其中Xi和Xj分别表示个体i与个体j的位置。一个种群中个体i受到合力是其引力和，定义为：

个体i的加速度为：

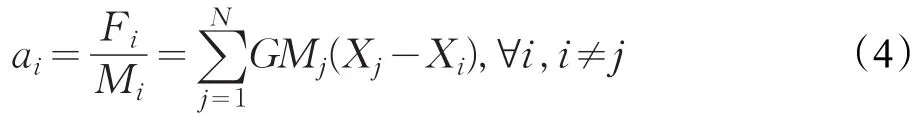
将式（4）中ai替换为位移对时间的二阶导数并展开：

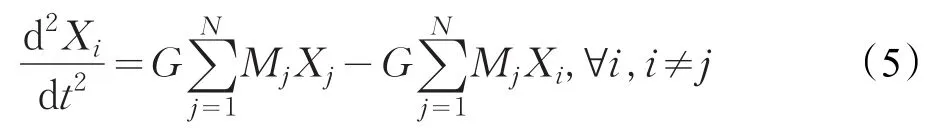
将公式（5）作为一个微分方程，对其求解得：

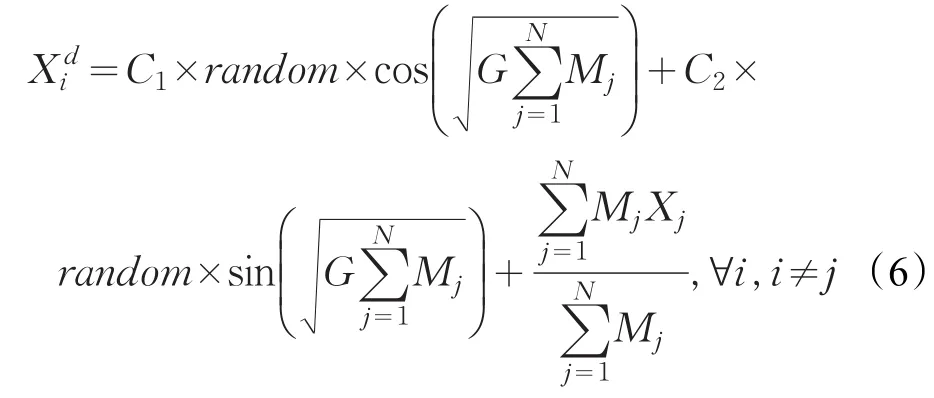
其中C1和C2为任意实数，变量t取1。random是一个范围为[0，1]随机数。引力常量G表示为：

其中G0为100，a为20，算法计算过程中当前迭代次数是iteration，最大迭代次数是MAXITER。

2.2 质量函数

在GMA算法中个体i的质量函数定义为：

其中f(Xi)表示个体i的适应值。对于求解最小值问题，f(Xbest)和f(Xworst)定义如下：

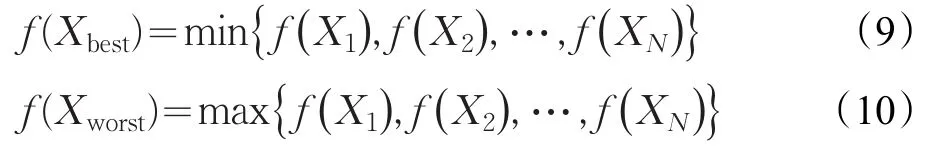
对求解最大值问题，f(Xbest)和f(Xworst)定义如下：

3 基于亲和度的引力移动算法

种群中各粒子质量的计算是引力移动算法中的最关键部分，在引力移动算法中粒子质量的大小是通过质量相关的函数适应值的大小来衡量的，作用粒子在质量大，适应值好，对作用力子吸引力大的粒子作用下逐步偏向质量较大的粒子。对于种群整体，作用粒子将受到群体粒子质量的影响，从而使作用粒子在群体粒子质量的影响作用下向粒子的最优方向移动。

根据以上算法思想的叙述可知粒子质量的大小与粒子受到合力的大小具有紧密关系。因此，改进算法通过改进粒子质量关系来改进粒子受到种群中其他粒子对该粒子的引力合力计算公式从而实现对粒子位置更新的引导。

3.1 基于亲和度的引力移动算法简述

根据上文对引力移动算法的分析，在改进的引力移动算法中通过在式（3）中添加系数λ来改进GMA中的粒子受到的合力计算公式。系数λ的计算公式为：

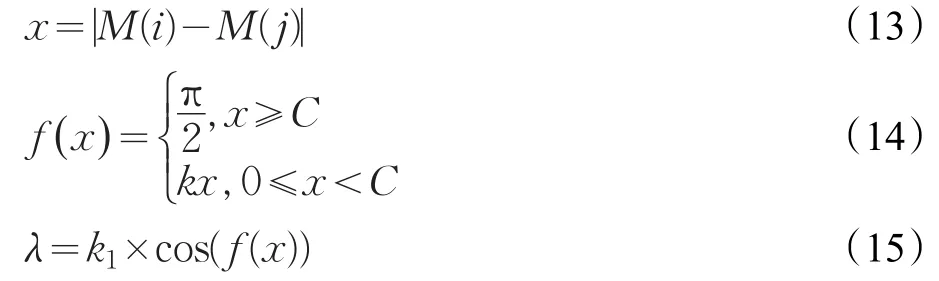
其中，λ为式（3）需要添加的系数；k1,k为可调整参数，在不同函数中设置不同的值；C为与k有关的参数，可通过C=πk-1/2计算。x的计算由式（13）得到，其中，M(i)和M(j)分别为粒子i和粒子j的质量；f(x)为一它由x得来的分段函数，通过式（15）可以使f(x)在[0,内变化。改进算法中设置x实现了函数值的亲和度检测。x值越小即两个粒子的之间的质量差越小，表示两个粒子之间亲和度越大，且两者之间引力越大；反之，两者之间的引力就越小。因此，将上式中设置的系数λ计算公式代入式（3）得到改进的引力移动算法的合力计算公式，表示为：

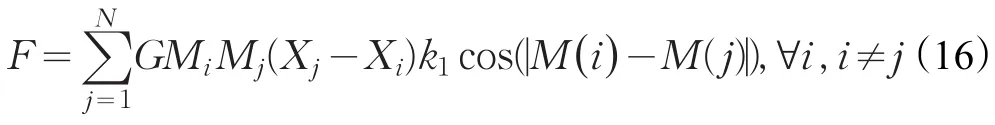
从式（16）可以看出，通过在引力移动算法中合力计算公式中添加λ，加快了算法的寻优速度。由于粒子的质量是由计算所得的目标函数的适应度值表示的，种群中粒子间目标函数适应度值大小越接近，粒子质量大小也就越相近，进而式（13）中x的值越小，且由式（15）可以得知，两个粒子之间的质量差的值越小，λ就越大，故将x代入式（15）计算得到一个系数λ的值就越大，相应的两个粒子间亲和度越大，进而粒子间的相互作用力也就越大，加快粒子向最优解偏移。

故由上文叙述分析知，改进的引力移动算法计算过程在基本算法每次迭代过程中首先计算粒子适应值，在计算得到新的适应度值的基础上，添加了一个修正适应值系数，削弱适应值差别大的粒子对作用粒子的影响，使得在粒子在寻优的过程中不容易陷入局部最优解，从而加速了寻优过程的进行。当种群两个粒子间适应度大小（即质量差）越相近时，粒子间的相互作用力也就越大，对作用粒子产生的加速度越大，作用粒子就会向对应粒子方向加速偏移，而当两个粒子间质量差很大时，粒子对作用粒子的作用力也就越小，对作用粒子产生相应方向的加速度就越小，粒子向着劣势方向的偏移就越小，在这种趋势下，整个种群就能更好地向最优解移动，理论说明改进的引力移动算法可以加速种群的收敛。

3.2 算法流程

步骤1初始化一个种群规模的大小为N，最大迭代次数设置为T，个体在可行域内中随机分布。

步骤2计算种群中每个个体在本次迭代后的适应值，确定种群中本次迭代后最优个体，更新最优个体及其适应值。

步骤3计算个体惯性质量及个体间的引力。

步骤4根据公式（13）计算种群中每个个体与种群中其他个体间质量差的大小。

步骤5根据公式（15）映射到区间，计算得到系数，得到粒子受到的合力。

步骤6根据公式（6）更新个体位置。

步骤7如满足终止条件则结束算法，否则返回步骤2。

4 实验结果分析

4.1 基准函数

为了测试该算法的优化效果，本文选取13个标准基准函数[17]来测试比较改进算法与基本算法的性能。基准函数如表1、表2所示。在表1包含的函数为高维单峰函数，在表2包含的函数为高维多峰函数。其中函数的维数用变量n代表，S是Rn的子集，表1、表2中的函数除了F8最小值为-418.982 9×n外其他函数的最小值均为0。

表1 高维单峰测试函数

表2 高维多峰测试函数

4.2 实验仿真

算法的实验仿真平台为Windows 10，MatlabR14a版本。本实验把改进后的算法与基本的引力移动算法进行结果对比。在以上情况下，假定两种算法种群的维度为30，种群规模设为50，最大迭代次数为1 000。对每个测试函数运行30次，统计测试30次后测试运行结果的中值、平均值和方差。

表3是式（14）、式（15）中的可调参数，可调参数是在仿真过程中多次测试后在稳定性和搜索精度结果相对最好的情况下确定的。对于表1、表2中的测试函数，运行结果分别如表4、表5所示。图1是F1优化结果曲线图，图2是F5优化结果曲线图，图3是F7优化结果曲线图，图4是F12优化结果曲线图，其中横坐标表示当前迭代次数，纵坐标表示每次迭代中取得的最好适应值的对数值。

表3 可调参数值

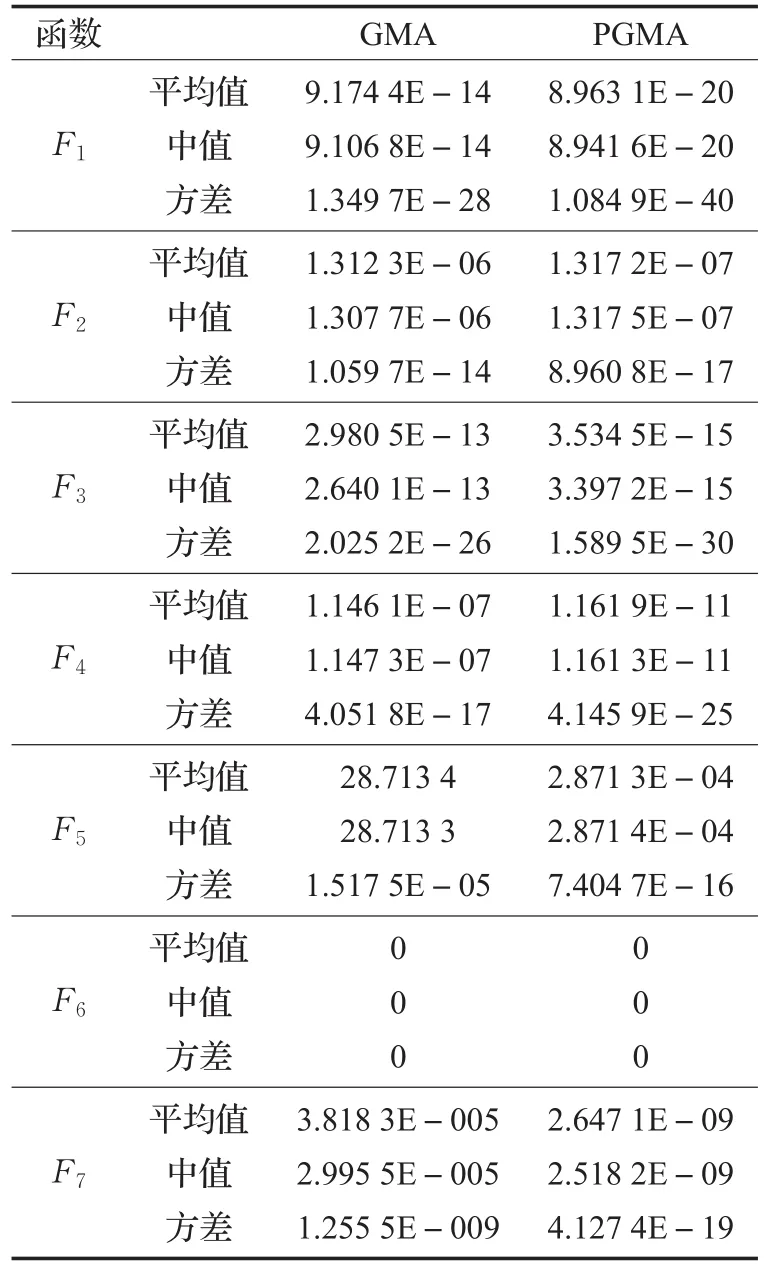
表4 高位单峰函数最小值搜索结果

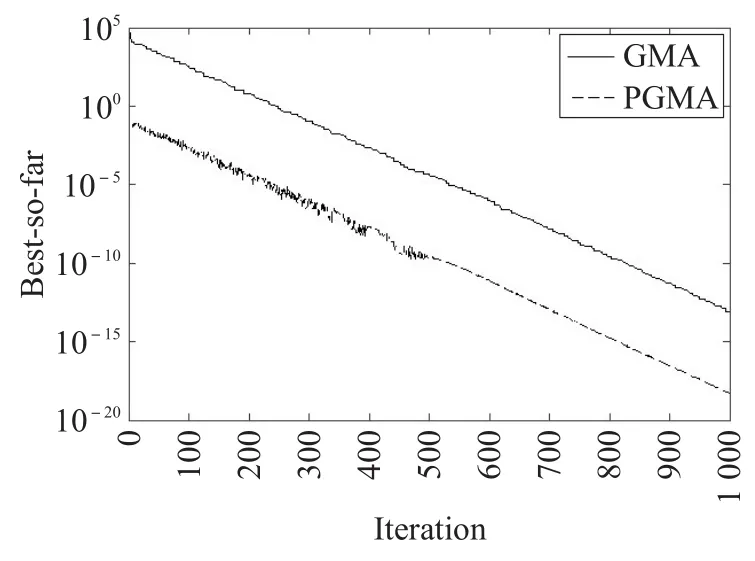
图1 F1优化结果曲线图

表5 高位多峰函数最小值搜索结果

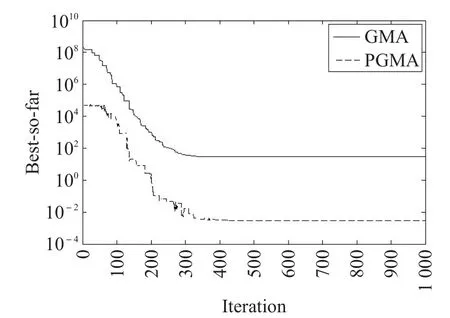
图2 F5优化结果曲线图

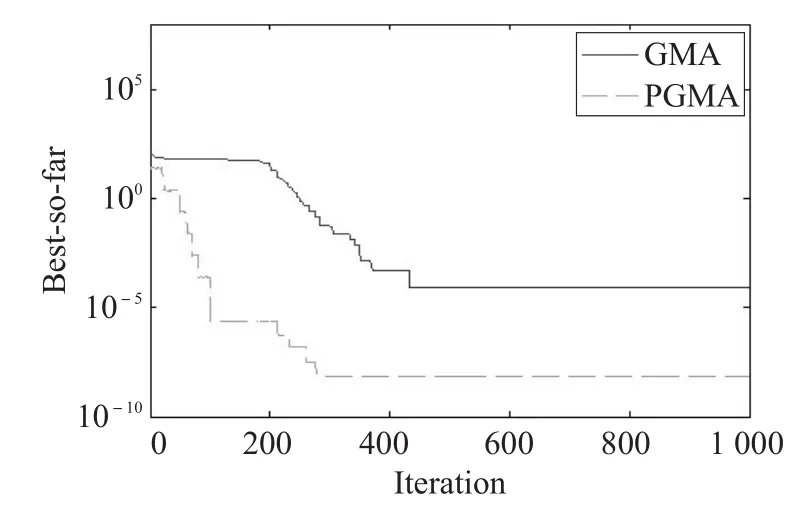
图3 F7优化结果曲线图

图4 F12优化结果曲线图

通过表4、表5数据以及改进前后GMA优化曲线对比可知，PGMA的收敛速度和最优值的精度均优于基本GMA算法。通过上文中算法的理论推理和仿真实验的结果可知，在可行域中搜索解的过程中粒子是不断寻找最优的，种群中每个粒子在其受到的来自种群其他所有粒子作用力叠加形成的合力作用下不断的移动。PGMA通过引进由粒子质量差的来表示亲和度，对基本GMA算法进行改进。在PGMA算法中采用减小质量大（即优解）的粒子对最优解的偏差，削弱质量小的粒子对质量大的粒子的作用力的方法，从而使得粒子更好更快地向着最优解的方向运动，进而提高了算法的搜索精度和稳定性。

5 结束语

本文对基本的GMA算法进行改进：在GMA算法基础上，针对其很难对问题求极小值进行了改进。在一个种群中，每个个体都在其他个体的引力作用而移动，在这种运动趋势下，整个种群中粒子最终达到一个平衡状态。个体在更新位置信息时，尝试改进了粒子受到种群中其他个体对其的合力的计算公式，优化了搜索精度，加快了算法的收敛速度。

本文使用13个基准函数对改进后的算法与GMA算法进行测试对比来验证改进算法性能PGMA提高。从实验结果可以看出，改进后的算法在稳定性和求解精度上均有更好的表现，验证了改进方法的可行性和有效性。

[1] Formato R A.Central force optimization：A new natureinspired computational framework for multidimensional search and optimization[C]//Proceedings of Nature Inspired Cooperative Strategies for Optimization（NICSO 2007）.Berlin，Germany：Springer，2008：221-238.

[2] Lin Y L，Chang W D，Hsieh J G.A particle swarm optimization approach to nonlinear rational filter modeling[J].Expert Systems with Applications，2008，34（2）：1194-1199.

[3] Dorigo M，Maniezzo V，Colorni A.Ant system：Optimization by a colony of cooperating agents[J].IEEE Transactions on Systems，Man，and Cybernetics，PartB：Cybernetics，1996，26（1）：29-41.

[4] Goldberg D E，Holland J H.Genetic algorithms and machine Learning[J].Machine Learning，1988，3（2）：95-99.

[5] Karakuzu J，Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Washington D C，USA：IEEE Press，1995：1942-1948.

[6] Rashedi E，Nezamabadi-Pour H，Saryazdi S.GSA：A gravitational search algorithm[J].Information Sciences，2009，179（13）：232-2248.

[7] Rashedi E，Nezamabadi-Pour H，Saryazdi S.BGSA：Binary gravitational search algorithm[J].Natural Computing，2010，9（3）：727-745.

[8] 谷文祥，李向涛，朱磊，等.求解流水线调度问题的万有引力搜索算法[J].智能系统学报，2010，5（5）：411-418.

[9] Yin M H，Hu Y M，Li X T，et al.A novel hybrid K-harmonic means and gravitational search algorithm approach for clustering[J].Expert Systems with Applications，2011，38（8）：9319-9324.

[10] 谷文祥，郭丽萍，殷明浩.模糊c-均值算法和万有引力算法求解模糊聚类问题[J].智能系统学报，2011，6（6）：520-525.

[11] 王宇，黄胜，廖全蜜，等.基于引力搜索算法的船舶舱室布置方法[J].上海交通大学学报，2016，50（1）：131-139.

[12] 陈梓铭.基于万有引力搜索算法的电力系统电压无功控制策略研究[J].华北电力技术，2016，35（5）：16-21.

[13] 蒋悦，沈冬梅，赵彦，等.基于引力搜索和分布估计的混合离散优化算法[J].计算机应用，2014，34（7）：2074-2079.

[14] 徐遥，王士同.引力搜索算法的改进[J].计算机工程与应用，2011，47（35）：188-192.

[15] 郑连斌，杨连贺.一种实现全局优化的引力移动算法[J].计算机工程，2015，41（7）：230-233.

[16] Spears W M，Spears D F，Heil R，et al.An over view of physicomimetics[M].Berlin，Germany：Springer，2005.

[17] Sarafrazi S，Nezamabadi-Pour H，Saryazdi S.Disruption：A new operator in gravitational search algorithm[J].Scientia Iranica，2011，18（3）：539-548.

ZHAO Ruijuan,YANG Lianhe.Improved gravitation move algorithm based on affinity.Computer Engineering andApplications,2018,54（6）：44-48.

ZHAO Ruijuan,YANG Lianhe

School of Computer Science and Software Engineering,Tianjin Polytechnic University,Tianjin 300387,China

To improve the searching performance of gravitation move algorithm,in accordance with problems of bad performance in search accuracy and slow convergence speed in the high dimensional space optimization,PGMA is proposed by introducing affinity to improve the algorithm convergence and search precision,and this improved Gravitational Move Algorithm（GMA）changes the particle’s gravitational force calculation formula.It includes the principles of gravitational move algorithm and the structure of the affinity,and the affinity for the appropriate transformation is added to the formula resultant force.Then the formula resultant force is modified.Thirteen benchmarks function are tested and show that new algorithm is better than GMAwith both a steady convergence and a better accuracy of solution.

Gravitation MoveAlgorithm（GMA）;resultant force;affinity;benchmark function;adjustable parameter

为提高引力移动算法搜索性能，针对引力移动算法解决一些高维空间优化问题时存在的收敛速度慢、搜索精度不高的问题，提出一种基于亲和度的改进引力移动算法PGMA。基于引力移动算法原理，通过构造一个基于亲和度概念的系数对种群个体受到的引力合力公式作适当的变换改造基本引力移动算法。改进后的算法对种群中个体的位置更新方向加以引导，来提高算法的搜索精度和算法搜索能力。用13个基准函数对改进算法进行试验验证改进算法在求解精度和稳定性上优于基本引力移动算法。

引力移动算法；合力；亲和度；基准函数；可调参数

2016-11-09

2017-01-02

1002-8331（2018）06-0044-05

A

TP301

10.3778/j.issn.1002-8331.1611-0158

天津市科技计划项目（No.16JCTPJC47400）。

赵蕊娟（1990—），女，硕士研究生，研究方向：数据挖掘、智能优化，E-mail：zhaorj_tjpu@163.com；杨连贺，博士，教授，博导，研究方向：数据挖掘。