特高含水阶段油藏水驱规律研究

黄迎松

(中国石化胜利油田分公司，山东 东营 257000)

0 引 言

陈元千[1-2]所建立的甲型和乙型水驱特征曲线，假设油水相对渗透率比值Kro/Krw与含水饱和度Sw呈线性关系，然而大量的现场实践表明，水驱特征曲线在高含水后期会发生上翘现象[3-5]。高丽[6]、刘世华[7]和宋兆杰[8]分别以直线、幂函数和抛物线对高含水期水驱特征曲线上翘后的数据进行了拟合，但均只关注岩心驱替过程的某一阶段，没有考虑到整个过程；只关注lg(Kro/Krw)-Sw关系曲线的外在形式，未进一步深入到微观驱替渗流过程寻找内在理论根源。因此，水驱特征曲线方法还缺乏稳固的理论基础，有待进一步完善。在前人研究的基础上，纵观水驱油的全过程，剖析了lg(Kro/Krw)-Sw关系曲线的本质，在此基础上建立了lg(Kro/Krw)-Sw关系曲线的新型表达式，据此，推导了新型水驱特征曲线关系式，并采用矿场数据证实了其正确性。

1 岩心驱替特征研究

lg(Kro/Krw)-Sw关系曲线反映了岩心驱替的过程。低含水期水相呈不连续状分布在孔隙边缘，黏性阻力、吸附阻力和毛管阻力突显，渗流条件较差，油相更易于流动，曲线呈上翘状；中含水期等渗点附近，油水两相均具有较高渗流能力，黏性阻力、吸附阻力和毛管阻力的影响较小，曲线近似为直线；高含水期油相呈不连续状分布于孔隙边缘，黏性阻力、吸附阻力和毛管阻力突显，渗流条件变差，水相具有渗流优势，曲线开始向下弯曲。

微观水驱油实验明确揭示了不同类型微观剩余油赋存量的变化规律(图1、表1)，剩余油饱和度越低，连片型剩余油比例减少，而多孔型、单孔型、油膜型剩余油比例增加。特高含水期，连通喉道轴向的驱动压力梯度不能克服多孔型剩余油和单孔型剩余油的黏性阻力和吸附阻力，因此，毛管力和剪切力不能有效作用于剩余油。对于油膜型剩余油，由于岩石表面亲油，油水共存于微孔隙内，水相流动作用于油膜的剪切力小于原油附着力，难以剥离油膜型剩余油。因此，在特高含水阶段，油相的流动能力急剧下降，这是水驱曲线发生偏转的根本原因。

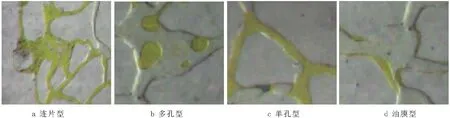
图1 剩余油微观剩余油类型

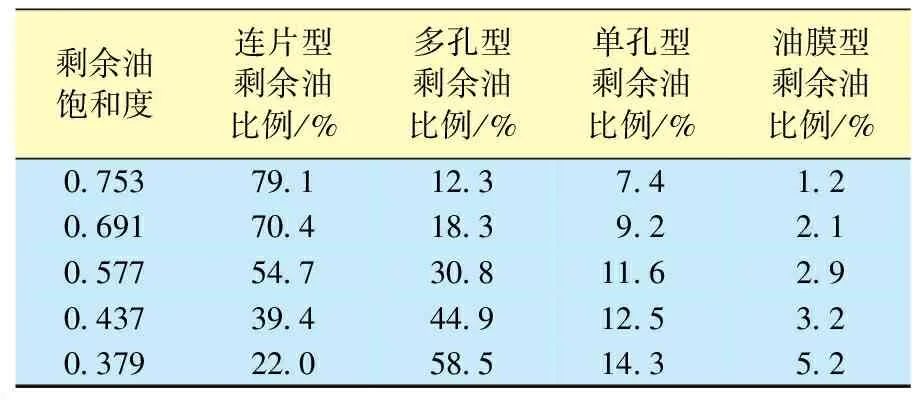
表1 不同类型剩余油相对比例与含油饱和度的关系

借鉴胜坨油田二区沙一区块、榆树林油田东14区块[8]和长庆西峰油田庄19井区岩心数据[10]，绘制出lg(Kro/Krw)-Sw关系曲线(图2)，表2为岩心数据。对lg(Kro/Krw)-Sw关系曲线用一元三次函数拟合，回归得到新型关系式(表3)。

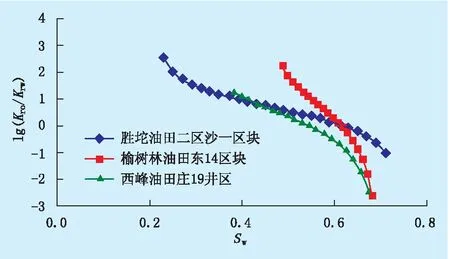
图2 不同油田区块lg(KV/Krw)-Sw关系曲线

由图2及表3可知，利用一元三次函数拟合lg(Kro/Krw)-Sw关系曲线效果较好。因此，以图2中曲线为例，验证新型lg(Kro/Krw)-Sw关系曲线对称中心与等渗点Si的关系。

表4为关系曲线对称中心及等渗点的对照关系。由表4可知，新型lg(Kro/Krw)-Sw关系曲线对称中心横纵标Xo值与等渗点Si值较为接近，二者呈正相关关系，表明新型lg(Kro/Krw)-Sw关系曲线对称中心具有等渗点的含义，而Xo与Si的差别是由各个环节的工程误差引起的。因此，新型lg(Kro/Krw)-Sw关系曲线可以描述岩心驱替渗流的全过程。

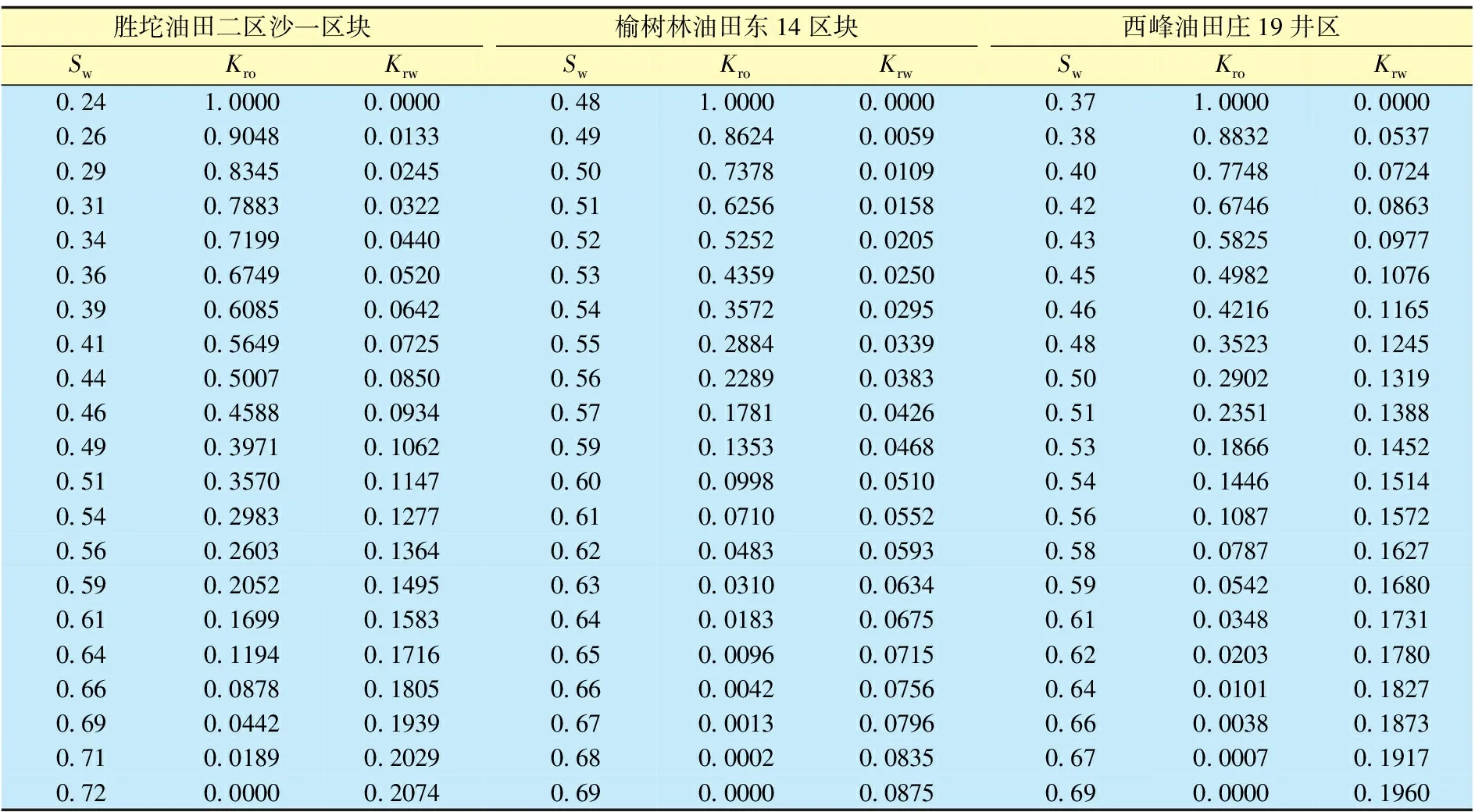
表2 不同油田区块岩心相对渗透率数据

表3 不同油田区块lg(Kro/Krw)-Sw关系曲线拟合结果

表4 对称中心横坐标Xo值与等渗点Si值对照

2 新型水驱特征曲线关系式的理论推导

现有水驱开发效果的评价方法较多[11-13],新方法依据lg(Kro/Krw)-Sw关系曲线的拟合结果进行理论推导，lg(Kro/Krw)-Sw关系曲线可以用式(1)进行描述：

(1)

式中：f、g、h、k为拟合系数；Kro为油相相对渗透率；Krw为水相相对渗透率；Sw为出口端含水饱和度。

将式(1)变形，可得：

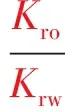
(2)

其中，a=-f，b=-g，c=-h，d=10k。

在不考虑重力和毛管力作用下，油水两相流动出口端Kro/Krw与油、水瞬时产量存在如下关系：

(3)

式中：Kroe、Krwe分别为油水两相流动出口端油、水的相对渗透率；Qo、Qw分别为日产油量、日产水量，m3/d；Bo为地层原油体积系数；Bw为地层水体积系数；γo、γw分别为地层原油、地层水的相对密度；μo、μw分别为地层原油、地层水的黏度，mPa·s；

由式(2)、(3)可得水油比[14]为：

(4)

式中：WOR为水油比。

应用Bukley-Leverett[15]前缘推进方程、Welge[16]方程和艾福罗斯实验理论研究成果，可以得到出口端含水饱和度和采出程度的关系为[1]:

(5)

(6)

式中：Soi为原始含油饱和度；Ro为采出程度，%；Swi为束缚水饱和度；Sor为残余油饱和度；ER为采收率，%。

将式(5)、(6)代入式(4)，两边同时取常用对数得：

(7)

将式(7)展开并简写为：

lgWOR=ARo3+BRo2+CRo+D

(8)

式中：A、B、C、D为拟合系数。

水油比与累计产油量关系式为：

(9)

(10)

(11)

(12)

(13)

式中：Np为累计产油量，104m3；N为原始石油地质储量，104m3。

式(8)、(9)为新型水驱特征曲线关系式，将经济极限水油比WORmax代入式(8)或式(9)，通过解一元三次方程可求得采收率或可采储量。

3 实例验证

以胜坨油田二区沙一区块为例，评价新型水驱特征曲线。该油藏含油面积为22.1 km2，石油地质储量为3 977×104t，油层平均有效厚度为22.1 m，孔隙度为32.1%，平均空气渗透率为4 900×10-3μm2，原始地层压力下原油体积系数为1.141 2，地层原油黏度为16.8 mPa·s。该油藏于1966年投入开发，截至2016年年底，单元综合含水率为97.0%，采出程度为40.0%。绘制该单元lgWOR-Ro关系曲线，并用新型水驱曲线关系式拟合。图3为lgWOR-Ro关系曲线及其拟合曲线。由图3可知，新型水驱特征曲线的拟合精度很高，相关系数达到0.998 9，拟合得到的新型水驱特征曲线关系式为：

lgWOR=35.48Ro3-41.73Ro2+19.24Ro-2.72

(14)

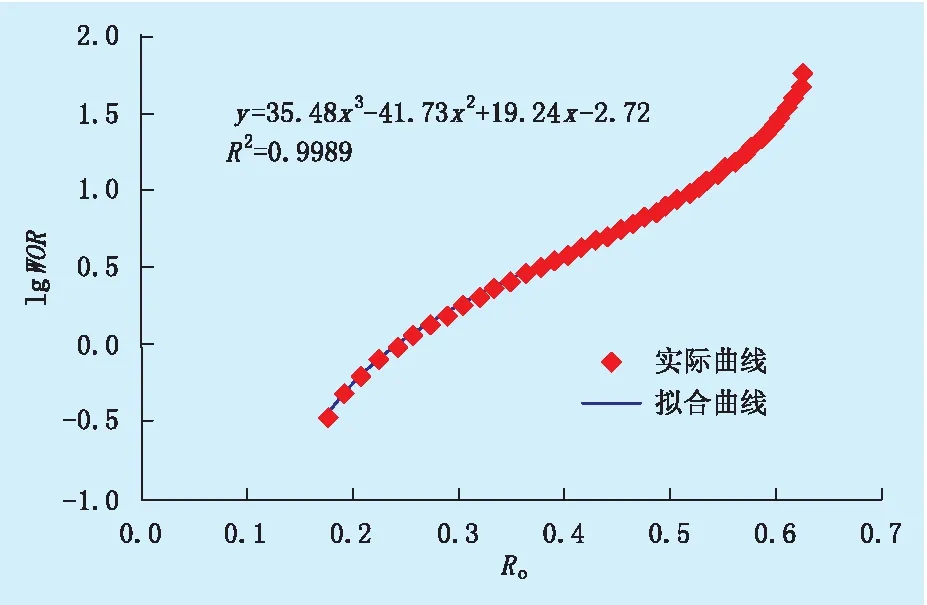
图3 lgWOR-Ro关系曲线及其拟合曲线

以经济极限水油比WORmax=49代入式(14)，可以预测最终采收率为0.627 0，物质平衡方法计算结果为0.622 0，两者误差仅为0.80%，表明新型水驱特征曲线具有较高的准确性。

若仅对水驱曲线上翘后的数据用新型水驱曲线拟合，其拟合结果如图4所示，所得到的拟合关系式为：

lgWOR=252.59Ro3-393.7Ro2+208.5Ro-36.47

(15)

以经济极限水油比WORmax=49代入式(15)，可以预测最终采收率为0.622 8，物质平衡计算结果为0.622 0，两者的误差为0.13%。其他水驱特征曲线的预测结果如表5所示。由表5可知，即使仅对水驱曲线上翘后的数据点进行拟合，新型水驱特征曲线的预测误差仍低于其他方法的预测误差。因此，新型水驱特征曲线具有更高的准确性和更强的适用性。

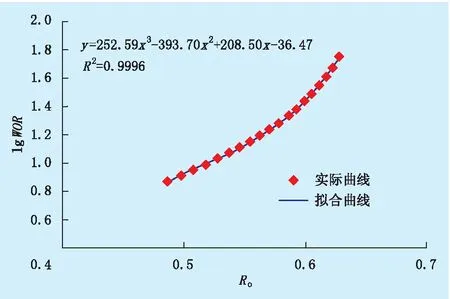
图4 高含水期lgWOR-Ro关系曲线及其拟合曲线

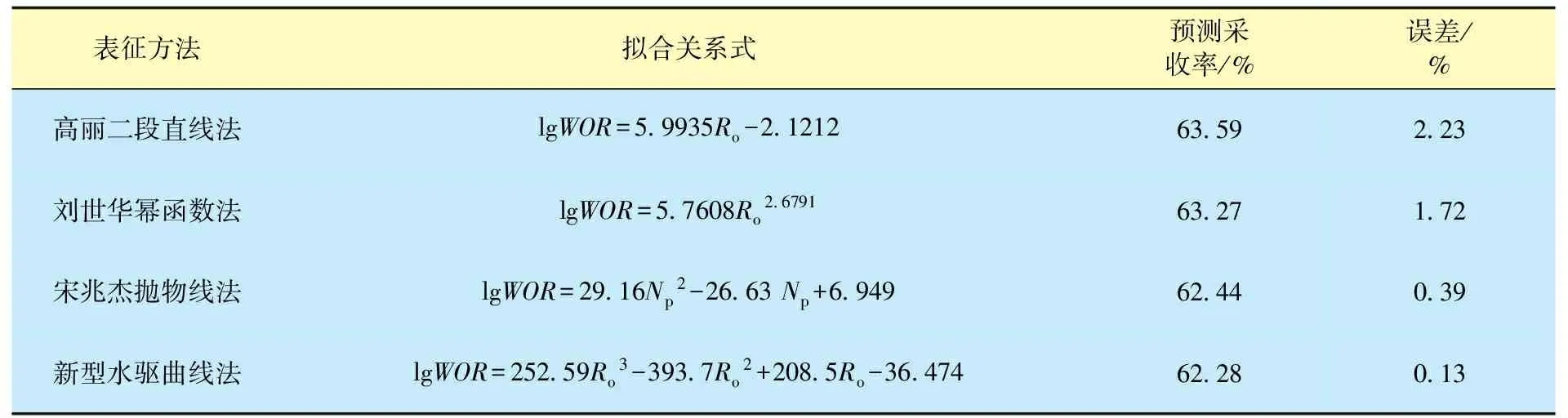
表5 高含水期不同表征方法lgWOR-Ro关系的拟合结果及预测采收率

4 结 论

(1)Kro/Krw与Sw在半对数坐标上呈三次函数关系，三次函数图像对称中心的横坐标与等渗点Si几乎重合，表明三次函数关系可以真正描述岩心驱替渗流的全过程。中含水期的直线段和高含水期的曲线段(二次抛物线或幂函数曲线)都只是三次函数关系图像的局部形态。

(2) 建立了新型水驱特征曲线关系式，即水油比与采出程度在半对数坐标上呈三次函数关系，新型水驱曲线关系式理论上适用于水驱油藏开发全过程。

(3) 与其他方法相比，新型水驱特征曲线法预测得到的采收率更为准确。

[1] 陈元千.水驱曲线关系式的推导[J].石油学报，1985，6(2)：69-78.

[2] 陈元千，陶自强.高含水期水驱曲线的推导及上翘问题的分析[J].断块油气田，1997，4(3)：19-24.

[3] 杨勇.高含水期水驱特征曲线上翘现象的校正方法研究[J].石油天然气学报,2008,30(3)：120-123.

[4] FENG Q,ZHANG J,WANG S,et al.Unified relative permeability model and waterflooding type curves under different levels of water cut[J].Journal of Petroleum Science and Engineering,2017,154(1)：204-216.

[5] 孙红霞.高含水期水驱特征曲线上翘新认识[J].特种油气藏,2016,23(1):92-95.

[6] 高丽，宋考平，马春华， 等.二段直线法预测高含水期油田开发指标[J].石油钻探技术，2008，36(5)：72-74.

[7] 刘世华，谷建伟，杨仁锋.高含水期油藏特有水驱渗流规律研究[J].水动力学研究与进展，2011，26(6)：660-666.

[8] 宋兆杰，李治平，赖枫鹏，等.高含水期油田水驱特征曲线关系式的理论推导[J].石油勘探与开发，2013，40(2)：201-208.

[9] 朱广笑.三次函数图象一定是中心对称图形么？[J].数学教学，2006，11(1) :18-20.

[10] 董大鹏.低渗透油田油水两相渗流机理研究[D].成都: 成都理工大学,2007.

[11] 陈军,冯桔,文涛.预测油藏开发中后期生产动态的新型水驱特征曲线[J].新疆石油地质,2007,28(5):596-598.

[12] 李巧云,张吉群,邓宝荣,等.高含水油田层系重组方案的灰色决策优选法[J].石油勘探与开发,2011,38(4):463-468.

[13] 陈元千.双曲线递减的简化及确定可采储量的截距法[J].天然气工业,1994，14(4):32-37.

[14] 姜汉桥，姚军，姜瑞忠.油藏工程原理与方法[M].东营：中国石油大学出版社,2006：239-241.

[15] BUCKLEY S E,LEVERETT M C.Mechanism of fluid displacement in sands[J].Trans AIME,1942,146(1)：107-116.

[16] WELGE H J.A simplified method for computing oil recovery by gas or water drive[J].JPT,1952,4(4)：91-98.