热轧卷材强制冷却过程热变形分析

李宝伟，孙艳红

1 前言

一般热轧卷在540～720℃的温度范围内绕成卷，随后送入仓库，在4～5 d内冷却至室温，用于后续过程的酸洗或直接供应市场。为了减少冷却时间并节省储存空间，大多数研究集中在各种强制快速冷却方法上，如浸水和喷水等快速冷却方法。大多数工厂发现，轧制后的卷材冷却至环境温度后，在开卷过程中观察到缺陷［1-2］，这些缺陷是由精加工机架中产生的轻微波纹造成的，随后发展出相当大的两面波纹，侧面波纹，卷材断裂等缺陷。生产中应避免这些缺陷，以确保热轧卷材具有优异的平整度，而不需要后续的处理校正。

过去几十年来，全球热轧卷材的快速冷却已经取得了一些重大的进展。Mazur等人比较了卷材的热特性，并用实验证明，热轧卷材水平堆叠的冷却时间要比垂直堆叠减少1.5倍。佩斯科夫等人认为通过适当的冷却时间，使用喷水法冷却后的热轧带材的机械特性可以提高，同时保留钢板的均匀性。假设主热流是沿着卷材轴线，并且将卷材放置在静止水中，是可以减少冷却时间而不影响冷轧过程中钢的质量。在改进卷材储存和运输方面，Thorn等人使用水冷数学模型来预测浸入水中卷材的冷却时间［3］。Gasho等人在稳定条件下获得了卷材冷却速率的对数关系［4］。

上述这些模型用于模拟卷材的冷却特性，通常集中在采用不同的强制冷却方法的冷却快速性上。由于其他性质主要依赖于温度场，确定热应力分布是解决卷材形状缺陷的重要步骤。此外，在将卷材强制冷却到环境温度后，应该注意在热轧卷材开卷期间的平整度缺陷。Nikitenko和Colas等人从微观结构演化观点来解释这个问题，研究表明，铁素体和奥氏体混合物在卷材冷却过程中的变化是导致平坦度缺陷的主因。

根据这些探索以及假设，本研究提出用热变形数学模型来预测卷材的温度场，尝试阐明当相变完成时，利用轧制后卷曲温度的退化机理，建立热轧卷材冷却过程中热传递和热变形分析的数学模型，以预测缺陷的发生和缺陷大小。模型引入了径向等效热导函数，这种函数与热轧钢板厚度、表面特性和压应力有关，并且包括周向应力和卷材张力。将测量数据与获得的数值模拟结果进行比较，结果表明：温度的轴向分布导致了局部热应力发生变化，并且增加了平整度缺陷。

2 热传递分析

图1为中空圆筒状的卷取钢板的热轧板卷传热和热变形分析模型。卷材强制冷却的数学建模可以假定除了周向以外的径向和轴向热流，也可以直接写在圆柱坐标系中的二维传热控制方程中：

式中：ρ为钢卷的密度，kg/m3；CP为钢的比热容，J/（kg·℃）；T为温度；τ为时间；γ为径向坐标；z为轴向坐标；kγ为径向热导率；kz为轴向热导率。

图1 传热和热变形分析模型

通常钢卷的温度沿轴向的热导率几乎与钢的导热系数相等，这是因为热轧卷材的钢层表面在接触点与可压缩气隙之间形成界面。其中有3种模式的传热，通过接触点传导、通过空气传导、通过间隙和辐射穿过缝隙。3种传热方式的不同，取决于卷层密度，卷材厚度和不同的强制冷却方法。

为此引入了等效热导函数的概念，假设两个钢带之间约有钢板厚度10%的恒定厚度的气隙。Baiketal根据由钢层、空气层和两个氧化物层组成的一个单位层的厚度导出作为径向正常压力的指数方程，此方程经过实验验证，并且径向方向上的热阻用下式表述：

式中：t为单位层厚度，RS为钢的耐热性，RO为氧化物和界面层，Rcd,S为通过接触点传导，Rcd,a为通过空气传导，Rrd为通过空隙辐射。上述等式考虑了表面特性的影响，并且测量氧化层的厚度。基于个体粗糙度的弹性行为理论，Greenwood通过统计模型描述了粗糙度。还有类似的方法，例如统计学被应用于热阻和外部负载之间的关系，Nlvikov提出并假设球面粗糙度高度的高斯分布。考虑到钢表面的局部高度和斜率以及压应力，Mikic进一步用比例因子修正了模型，得出了以下方程：

式中：ts为钢的厚度，tO为氧化物层的厚度，kS为钢的导热系数，tanθ为轮廓的绝对斜率的平均值，σp为剖面高度的标准偏差，A为实际接触面积与表观接触面积的比值，P为公称压应力，ε为辐射系数，S为斯忒藩—玻耳兹曼常数（5.67×10-8W/m2K4）。

关于控制方程（方程1）的初始条件t=0，T（r，z）=T0。考虑到一些边界条件，如图1所示，每个卷材具有4个表面，即内表面、外表面和两个边缘表面，通过这些表面向周围进行热传递。因此，这些条件可以表示为：

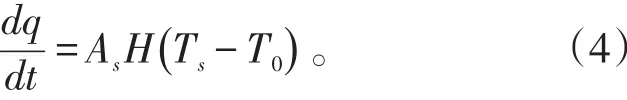
式中：d q/d t为表面热流，AS为卷材的表面积，TS为表面温度，T0为环境温度，H为传热系数。

3 热变形分析

尽管初始卷绕张力不能在热轧卷材中，但是径向热应力的作用考虑了层间压缩压力。因此，剥离层和中间层被认为压力在它们之间没有形成，并且在冷却过程开始时，没有重力在同心薄壁圆柱体上。随着强制冷却过程的进行，由于局部收缩和热应力导致平坦度缺陷。另一方面，由于在热传递分析中热轧卷材的环向应力被忽略，因此在卷曲过程中相继卷绕的钢板有带状凸起和冠状带，这些将导致卷材边缘处形成间隙，卷材产生不均匀的张力和环向应力。因此，考虑到卷取过程中的带状凸起，变形分析时可以将压缩压力表示为环向应力和卷取张力的函数：

式中：P（z）为压缩压力，σθ()z 为环向应力，t（z）为条带的轴向厚度分布，t为条带的轴向厚度初始值，-r为平均圆柱体的半径，rn（z）为薄的圆柱体半径，α为凸起比率，n为凸起指数，h为钢条半宽度。

4 结果与讨论

内部应力的分布及其对加工张力、层数和钢带材料特性等参数的依赖性在很大程度上决定了热轧卷材的质量和平整度缺陷。因此，这些模型可用于评估热轧卷材在强制冷却期间不同参数变化时可能发生的残余应力的不同分布。在控制方程（方程1）的解中采用的是有限差分法，其中卷材尺寸，卷曲温度，仓库中的定位姿态，使用的冷却方法及其应用的开始和结束时间的初始条件都被给定了数值，然后这些数值在每个时间间隔内都要运行。因此，利用热轧板卷内的热传递和各径向的宽度为600 mm，轴向长度为1 000 mm的各条带之间的压缩压力，计算出应力和应变。为了验证这些模型，使用了ABAQUS软件。图2比较了模拟结果和卷材中间宽度测量的外表面残余应力，可以看出，如果忽略层流冷却对失效的影响，边缘处的拉伸应力比其他应力高得多。图3给出了轴向耦合热机械应力的分布，对平直度缺陷有显著影响。图4是应变设备测量真实卷材的测量结构示意图。

5 结论

建立了热轧卷材冷却期间的热传递和热变形分析的数学模型，用来研究从轧制结束到室温的冷却过程中平整度缺陷的问题。得出的结论是：对于允许相变达到完全的给定的低卷曲温度，温度的轴向分布主要引起局部耦合热机械应力的变化，并且增加平整度缺陷。模型的结果表明，残余应力的分布，将导致冷却至室温时有双侧波纹的形成。未来的研究将面向如何应用最先进的方法来解决轮廓缺陷问题，同样地，建立热机械和微观结构演化综合数学建模可视化这些机制，有利于提高产品制造的质量。

图2 径向热应力分布

图3 轴向耦合应力分布

图4 测量结构示意图

［1］ E.Nikitenko,B.C.Gris.A mechanism of post-rolling deterioration in hot band flatness during coiling［J］.Iron and Steel Technology，2009，6（10）：60-63.

［2］ V.L.Mazur,V.I.Meleshko,V.V.Kostyakov,etal.Efficient schedules for forced rapid cooling of coils of hot rolled strip［J］.Steel in the USSR，1989，19（9）：162-165.

［3］ T.R.Tauchert,D.C.Leigh,M.A.Tracy.Measurements of Thermal Contact Resistance for Steel Layered Vessels［J］.Journal of Pressure Vessel Technology，1988，110（8）：335.

［4］ E.G.Gasho,V.I.Prokhorov,A.T.Moroz,et al.Cooling Conditions of Hot Rolled Steel Coils［J］.Steel in the USSR，1987，17（2）：86.