基于极限状态设计法的安全空气塞织物结构参数的研究

东华大学纺织学院，上海，201620

如今，人们在享受地铁交通带来便捷的同时，也面临着自然灾害的威胁，如洪水[1]。洪水一旦爆发，地面排水系统若不能及时将水完全排出，则洪水会冲进地铁隧道内，这不仅会引发电路损坏、列车停运等社会危害，更有可能造成重大的经济损失，甚至危害到人们的生命安全。近几年，国内外都在致力于研究一种可充气式胶囊型安全空气塞织物，用以抵挡洪水的入侵[2]。它是一种以圆柱体为主体的管状织物，圆柱体的两端为直径不断发生变化的球冠形织物，故整体与胶囊的形状相似(图1)。

图1 胶囊型安全空气塞织物

这种安全空气塞织物结构简易、设置灵活、安全可靠。洪水来袭时，感应装置启动，安全空气塞织物开始充气直至完全膨胀，即呈胶囊形；然后，该安全空气塞织物与隧道内壁完全接触，密封住隧道内的一节，即可阻挡洪水的入侵[3]。因此，为使安全空气塞织物能抵御洪水的冲击且不产生滑移，织物的充气压力和强度需满足一定的条件，且织物的轴向稳定性即安全空气塞织物与隧道内壁的摩擦力也需达到一定的要求。

本文旨在使用极限状态设计法[4]对安全空气塞织物进行一系列结构参数的设计，研究安全空气塞织物的充气压力、强度及轴向稳定性[5]，使之达到抵御洪水冲击的要求。

1 极限状态设计法

极限状态设计法采用一个数值对应描述一种随机变量，这个值称为基础值xp， q。对于抵抗力来说，定义一个固定的区间(xp， q， ∞)，使抵抗力的样本数在总样本数中占据一个固定的比例f(f<1.00)。换句话说，当置信度为q时，100f%的值比基础值xp， q大，100p%的值比基础值xp， q小(其中，p=1-f)。本文选用C-basis[6]确定q=0.95、f=0.95。

在极限状态设计法中，习惯用局部系数φ和平均值x的乘积表示基础值xp， q。对于抵抗力而言，基础值xp， q=φRR(其中，φR为抵抗力系数，R为抵抗力)；对于负载而言，基础值xp， q=αLL(其中，αL为活负载系数，L为活负载)。

极限状态设计法将极限状态分为正常使用极限状态和承载能力极限状态[7]。设计安全空气塞织物是为了能安全地承受洪水冲击带来的负载，而这种负载可能会导致安全空气塞织物结构的失效，因此需考虑织物的最大承载能力，故本文采用承载能力极限状态设计法。

使用两个变量描述安全空气塞织物的力学性能——织物的抵抗力和织物承受的负载。当安全空气塞织物完全被充气时遭受洪水冲击，则织物需满足[8]：

φRR>αDD+ψγ(αLL+αTT)

(1)

式中：αD——死负载系数；

D——死负载；

ψ——负载组合系数；

γ——重要因数，用于解释那些无法预测和无法解释的系统故障；

αT——热量负载系数；

T——热量负载。

安全空气塞织物工作时主要承受两种负载——充气压力和洪水冲击压力，且两者都属活负载，因此安全空气塞织物未受到死负载的作用。且洪水温度一般考虑为室温，故安全空气塞织物也没有受到热量负载的作用。因此，式(1)可简化成

φRR>ψγαLL

(2)

故作用于安全空气塞织物上的两种负载对织物结构定义了三种不同的极限状态[9]：

(1) 织物内部的充气压力Pi足以抵抗织物外部受到的洪水冲击力Pe；

(2) 织物的强度R(即抵抗力)足以抵抗织物本身受到的综合应力N；

(3) 织物的结构在抵抗洪水冲击时能一直保持轴向稳定性。

1.1 充气压力的设计

充气压力是指安全空气塞织物被充气达到它所设计的形状时，织物内部受到的最大充气压力。且当安全空气塞织物受到洪水冲击时，织物的充气压力可抵御洪水冲击压力，因此织物的充气压力Pi必须大于洪水冲击力Pe才可维持上游处织物的几何稳定性。如果Pi小于或趋近于Pe，则洪水可能会从安全空气塞织物外侧漏出，这会减小安全空气塞织物与隧道内壁的接触，致使完全失去摩擦力，安全空气塞织物失去抵御效果。在洪水的下游处，安全空气塞织物只受充气压力的作用，因此，为减小安全空气塞织物受到的负载，充气压力应在满足抵御能力的前提下尽可能地小。故根据式(2)可知充气压力和流体压力之间需满足：

φPiPi>ψγαLPe

(3)

其中，φPi为抵抗系数。φPi=1-φ-1(f)CV，αL=1+φ-1(f)CV。φ-1(f)是正态分布概率函数的一种表示；CV为变异系数，其值为样本数据平均值与标准偏差的百分比。

由于本文的研究不涉及死负载，只有活负载，所以负载组合因子ψ=1。根据式(3)可知Pi的取值范围：

(4)

1.2 织物的强度设计

研究表明，织物涂层后的双轴向拉伸强度和单轴向拉伸强度相等。因此，本文的织物的强度R取单轴向拉伸强度。

根据织物应力的计算方法，假设织物为不能伸展的物体，充气结构的几何形态没有明显的变化，则织物上的应力是均衡的。胶囊型安全空气塞织物在几何形态上主要有两个曲率半径——r1和r2。根据拉普拉斯(Laplace)等式，可知原则上最大应力综合N：

(5)

式中：ΔP——充气安全空气塞织物横截面的压力微分。

对于织物，习惯用最大应力综合N代替应力σ。对于球体，r1=r2=r；对于圆柱体，r1=r，r2=∞。则

(6)

N圆柱体=rΔP

(7)

安全空气塞织物的圆柱体部分与隧道内壁紧密接触，因此圆柱体上的负载会直接传递到隧道内壁的表面，故安全空气塞织物承受的最大应力综合在下游的织物球面上，即ΔP=Pi。根据式(2)，织物的强度应满足：

φRR>ψαLN

(8)

另外，因本文研究的安全空气塞织物只受到活负载作用，未受到死负载作用，所以ψ=1。再结合式(6)和式(8)可得安全空气塞织物所需的强度R：

(9)

1.3 织物的轴向稳定性的设计

安全空气塞织物与隧道内壁接触的部分为圆柱体。设接触长度为Lc，为保持安全空气塞织物与隧道内壁间紧密接触，安全空气塞织物与隧道内壁的轴向压力Fr：

Fr=μPiSLc

(10)

式中：μ——摩擦系数；

S——圆柱体周长；

Lc——接触长度。

安全空气塞织物受到的外界压力是由洪水冲击力Pe和下游压力P0所产生的。假设大气压即为下游压力P0，则安全空气塞织物受到的轴向负载Fα：

Fα=PeA

(11)

式中：A——隧道内横截面积。

在已知隧道内壁半径r1=r2=r的情况下，S=2πr，A=πr2，故式(10)和式(11)中的S和A都是确定的参数。根据式(2)可得：

φFFr>ψαLFα

(12)

式中：φF——轴向压力的影响系数。

联立式(10)、式(11)和式(12)可得：

φμμφPiPiSLc>ψαPePeA

(13)

式中：φμ——摩擦系数的影响系数；

αPe——洪水冲击压力的系数。

因本文研究的安全空气塞织物未受到死负载作用，只受到活负载作用，所以ψ=1。则根据式(13)可求出安全空气塞织物圆柱体部分与隧道内壁接触的长度Lc需满足：

(14)

故从式(14)可知，充气安全空气塞织物结构与隧道内的轴向稳定性取决于安全空气塞织物圆柱体部分的长度。

2 结构参数的确定

下文将计算出安全空气塞织物的结构参数。安全空气塞织物的规格要求：

(1) 胶囊形状；

(2) 织物紧度E=77%；

(3) 模拟洪水冲击试验管道半径r=3 cm；

(4) 洪水冲击压力Pe=207 kPa。

2.1 充气压力

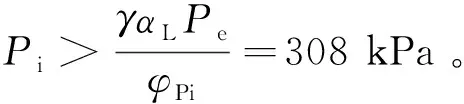
故取充气压力Pi=310 kPa。

2.2 织物的强度

织物的强度可根据式(9)计算，其中模拟洪水冲击试验管道半径r=3 cm，Pi=310 kPa。计算时，充气压力相当于负载且CV=10%，则αL=1.128。

并根据目标胶囊型安全空气塞织物尺寸，上机织造了结构参数与其相同的且紧度为77%的平面织物，并测量了平面织物的强度(表1)。

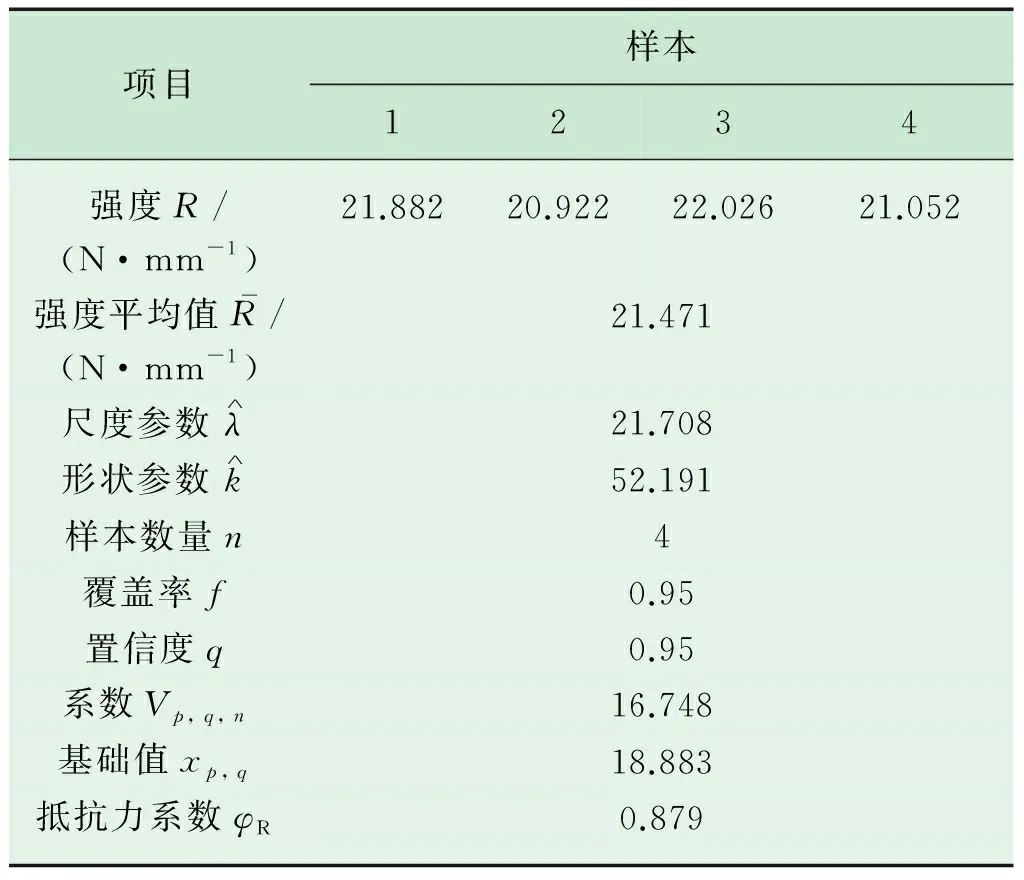
表1 织物的强度测量值及分析

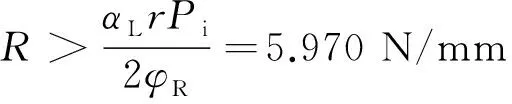
结合表1可知，织物的强度平均值为21.471 N/mm>5.970 N/mm，满足安全空气塞织物的强度要求。

2.3 织物的轴向稳定性

安全空气塞织物与管道内壁的摩擦力由织物圆柱体部分的长度决定，计算织物与管道内壁的摩擦力需先计算织物圆柱体部分的长度。因此，洪水来袭时，为保证安全空气塞织物在管道内壁之间的轴向稳定性，织物的圆柱体部分与管道内壁的接触长度Lc应满足一定的要求。Lc可根据式(14)计算，其中管道半径r=3 cm，Pe=207 kPa，Pi=310 kPa。充气压力相当于抵抗力且CV=10%，则φPi=0.872。洪水冲击压力相当于负载且CV=5%，则αPe=1.082。

安全空气塞织物与管道内壁之间的摩擦系数测量值如表2所示。

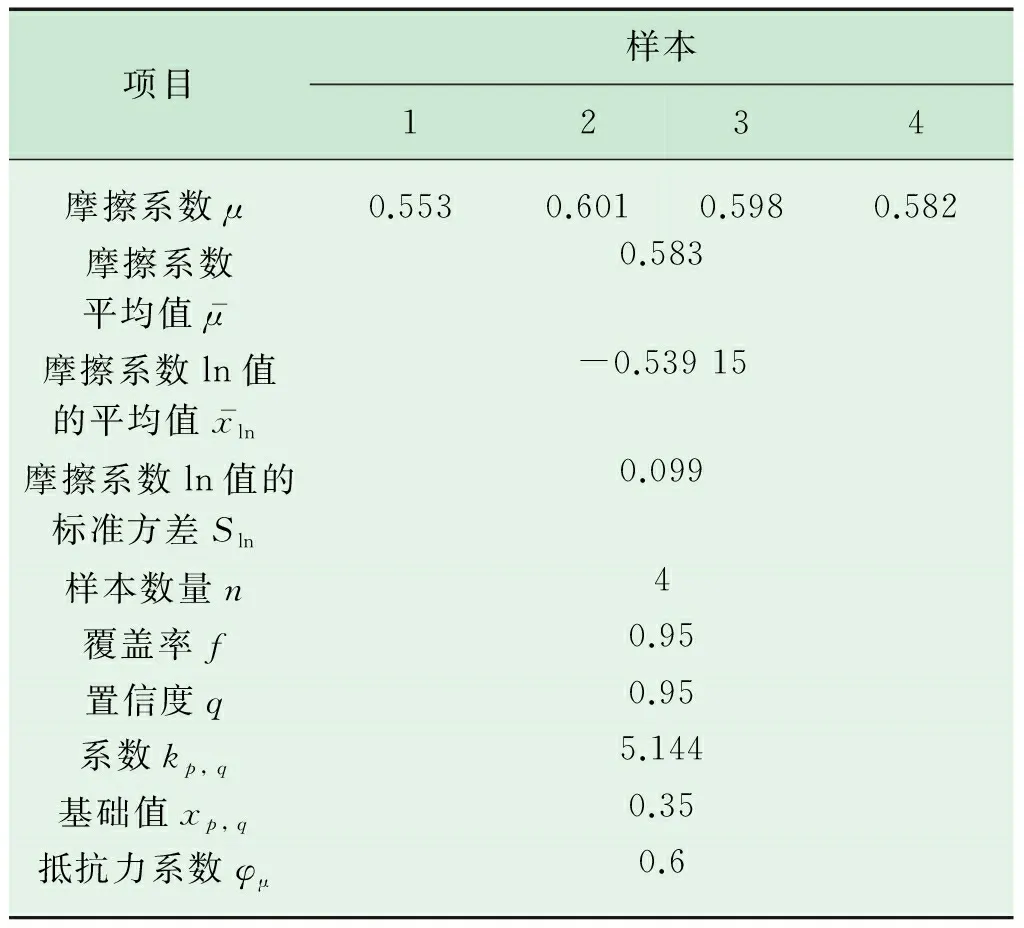
表2 织物与管道内壁之间摩擦系数的测量值及分析

故织物圆柱体部分的长度Lc取0.040 0 m。

3 结 论

本文通过极限状态设计法，对安全空气塞织物的充气压力、强度及轴向稳定性进行研究和计算，得出：在模拟洪水冲击试验的条件下，安全空气塞织物的充气压力需达到310 kPa，织物圆柱体部分的长度需大于0.035 5 m。通过制备紧度为77%的织物发现，织物的强度平均值为21.471 N/mm>5.970 N/mm，即织物具备的强度远大于安全空气塞织物所需的强度，且在充气压力取310 kPa、织物圆柱体部分长度取0.040 0 m时，安全空气塞织物理论上能抵御洪水冲击。

[1] INOUYE R R， JACOBAZZI J D.Great Chicago flood of 1992[J]. Civil Engineering ASCE， 1992， 62(11)： 52-55.

[2] ALLISON B. Going underground： Homeland security works on tool to prevent tunnel disasters[J/OL].FoxNews，2008-09-05.http：//www.foxnews.com/story/0，2933，417461，00.html.

[3] MARTINEZ X， DAVALOS J， BARBERO E J， et al. Inflatable plug for threat mitigation in transportation tunnels[C]// SAPME. Baltimore MD： Williams and Wilkins， 2012.

[4] 郭云志，王欣，高顺德，等.极限状态设计法及应用[J].建筑机械，2005(5)：67-69.

[5] BARBERO E J， SOSA E M， MARTINEZ X， et al. Reliability design methodology for confined high pressure inflatable structures[J]. Engineering Structure， 2013，51(6)：1-9.

[6] BARBERO E J， GUTIERREZ J M. Determination of basis values from experimental data for fabrics and composites[C]// SAMPE. Baltimore MD： Williams and Wilkins， 2012.

[7] 沈其明，邓和平.结构设计中的容许应力法和概率极限状态设计法[J].重庆交通学院学报(自然科学版)，1985，4(2)：12-17.

[8] NRCC， National building code of Canada[J/OL].National Research Council of Canada，2005-01-01.http：//www.nrc-cnrc.gc.ca/eng/ibp/irc/codes/05-national-building-code.html.

[9] POMBO J C M. Mechanical characterization of fabrics for inflatable structures[D]. Morgantown： University of West Virginia， 2008.