湘西州柑橘产出影响因素实证分析

毛 政 ，张启胜

（湖南农业大学 a.经济学院；b.法学院，湖南 长沙 410128）

1 问题的提出

柑橘栽培历史悠久，并在世界近150个国家和地区有种植，据联合国粮农组织数据显示，全球柑橘种植面达7×106hm2，年产量超过1亿t。当前，我国柑橘产业在政府的扶持和号召下也得到了长足发展，不仅为农民增收、脱贫致富发挥了重要作用，也为改善生态环境作出了积极贡献。因而吸引了众多学者对柑橘进行大量研究.如曾柏全，邓子牛等对湖南宽皮柑橘的血缘与起源关系进行了研究[1]。也有专家为提高柑橘附加值费尽周折，如白婕，李娟，张靖对柑橘进行深度开发和综合利用作了大量研究[2]。熊巍，祁春节及张炳亮则选用DEA 模型方法对我国柑橘产业产出效率进行测算与分析[3-4]。宋金田，祁春节在我国柑橘主产区进行了实地调查，从柑橘种植意愿出发，分析了柑橘种植影响因素[5]。汤荣丽运用DEA-Malmquist指数分析方法对我国柑橘全要素投入产出效率作了分析[6]。栾好安及钟冰，陈远喜认为柑橘应该使用绿色肥料，不仅对生态有好处，更能提高柑橘品质，进而提高柑橘的经济效益[7-8]。张建春认为影响柑橘产量的主要因素为病虫害；干旱内涝及冰冻影响[9]。为防止病虫害对柑橘产出造成影响，许多柑橘种植户使用了农药，彭湘莲等从食品安全角度从发，分析了柑橘使用农药的影响[10]。

结合众多学者对柑橘产出影响因素的研究，本文从湘西州柑橘种植实际情况出发，综合劳动力、科研、柑橘种植面积，劳动力素质、土地使用成本、化肥、农药等柑橘产出影响因素借助并拓展柯布——道格拉斯生产函数来研究湘西州柑橘产出问题。

2 研究方法

2.1 建模前必要的假设

模型是一种理想化的理论工具，但在实际的计算和分析过程中，建模会存在着众多的不确定性因素，为确保一定的理想化效果或者说为使建模不确定因素最小化，在建立模型之前，我们往往会根据实际情况做出一定的假设条件。

第一，假定所选择的各个影响柑橘产量的因素在其他因素不变的条件下每增加一个单位所带来的产量变化是恒定的，即有固定的产出系数。

第二，假定每一柑橘产量影响因素对产出的影响之和为这些影响因素的综合影响值，即各个产出影响因素之和为共同影响值。

第三，假定在时间序列上柑橘产量发生一定的变化误差仅仅是因为随机扰动项的存在而已，对一些不可抗拒的因素如干旱、洪水等自然灾害的影响因素不作考虑。

第四，假定政府对柑橘产业的相关政策不发生变化、柑橘相关产品价格不变，也即认为人为观点对柑橘产业不发生变化。虽然这些相关因素在柑橘生产过程中确实客观存在，但由于这些影响因素的作用把引起柑橘产出增加的那一部分应该归结于柑橘生产技术进步所带来的产量变化之中，在本文后面的扩展C-D函数模型中将有所体现，具体的处理措施是加入时间变量T，然后计算其弹性。

第五，假定各个对柑橘产量影响的因素之间无相关性。即Rij=0（其中i≠j）。事实上，各个影响因素之间不可能不存在关联性，为了避免各影响因素的多重共线所带来对模型进行识别和分析的麻烦而进行此必要的假设。

2.2 柑橘产出变量的设置

柑橘的产出从理论上与“柯布——道格拉斯生产函数”模型具有一致性，都具有“生产性质”，在柯布——道格拉斯生产函数模型中，只有两个影响因素：一是劳动力，二是资本。但柑橘产出的影响因素远远大于两个，这里将对柑橘产量的影响因素分为：劳动力、科研经费投入、种植规模、劳动力素质、土地成本、化肥、农药以及其他投入。劳动力投入：从西方经济学的相关理论可知，劳动力与土地、资本是影响产出的三大要素，即劳动力是其中之一。事实上柑橘产业的某些环节是劳动密集型产业，比如柑橘果实采摘过程中就属于这样的环节，在这样的环节中就要投入较多的人力。科研经费投入：在柑橘产业的链条中，对柑橘品种的科研显得越来越重要，因为柑橘消费者的喜好决定着柑橘销售量，从而可知对柑橘科研经费投入的多少，直接影响到柑橘产品的销售量，并最终反映到柑橘种植规模；种植规模的大小可以用种植面积进行度量，事实上种植规模还会对柑橘的品牌有一定影响，从而对柑橘生产销售会产生直接影响，可见种植规模也是柑橘生产的一大影响因素。劳动力素质：正如前面所言，柑橘产业在一定程度上是劳动密集型产业，但同时也是一项技术密集型产业，劳动力包括政府对柑橘种植进行指导的科研人员、管理人员及种植从业人员，然而对柑橘产业中的某些技术环节（如柑橘幼苗嫁接）来说，劳动力的素质也在影响着柑橘产业，也是柑橘产出的一大影响因素。对劳动力素质这一定性的概念进行量化可依据文化程度给出量化值，具体量化值可见表1。土地投入：柑橘生产基地的多少，使用土地面积的大小及土地使用成本的高低，这些都会直接影响柑橘的产出效率。化肥的投入：科学实践表明柑橘的养分吸收量比一般的农作物都要大。可见要柑橘产量高，就满足种植柑橘的土壤比较肥沃，而土壤的肥沃程度因地而异，其肥沃程度差异却客观存在，自然肥沃程度越好，柑橘产量会越高，反之则需化学肥料进行改善。但化肥并不是投入越多越好，过多的化肥反而会使柑橘产量降低。农药投入：柑橘产业也是农产品产业，也不可避免地碰上柑橘的病、虫、掉果等生物灾害发生，为防止此类灾害发生，有必要投入一定量的农药。其他投入：除了上述投入之外的其他一些比较大的投入。

表1 劳动力素质量化值Table 1 Quantitative table of labor quality

3 湘西柑橘产量模型的构建

3.1 湘西柑橘产量模型的选取

本文选择的是柯布——道格拉斯生产函数模型，柯布——道格拉斯生产函数（简称C-D生产函数）是当前应用最为广泛的一种生产函数，它是1928年由芝加哥大学经济学家道格拉斯（P·H·Douglas）与数学家柯布（C·W·Cobb）共同研究出来生产模型，他们以1899—1922年的美国制造业真实数据资料为背景，得出以下数理模型：

式中，Q代表产出量；L代表劳动投入量；K代表资本投入量；A代表效率系数；α代表资本的产出弹性（0＜α＜1）；β代表产出系数（0＜β＜1）。

可以由模型（1）推导出柯布——道格拉斯生产函数相关特征：

①资本和劳动作为两个解释变量，具有相互依存性，也即两者共同作用，才能有所产出，若其中任何一个解释变量为0，则被解释变量产出也必然为0。

②资本边际产量与劳动边际产量都会大于0。

其中，劳动的边际产量：

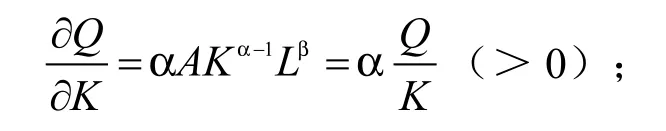
资本的边际产量：

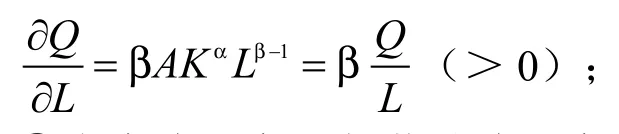
③资本边际产量与劳动边际产量都呈现单调递减趋势。因为：

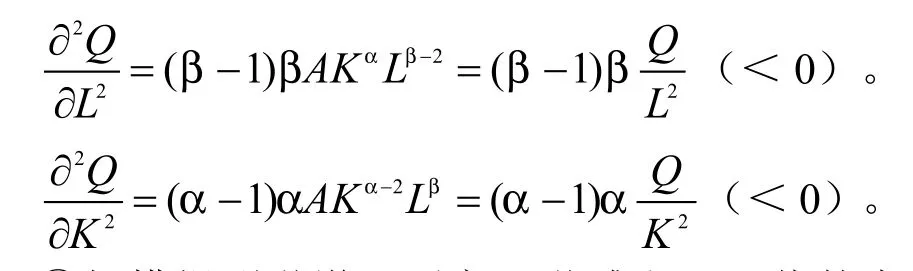
④规模报酬递增、不变及递减由α+β值的大小来决定。也即当α+β＞1时规模报酬呈递增趋势；当α+β=1时规模报酬不变；当α+β＜1时规模报酬呈递减趋势。

3.2 模型的改进

柯布——道格拉斯生产函数Q=AKαLβ简单明了，可是在实际应该过程中却存在着许多的不足，比如在研究农产品生产过程中，其解释变量因素不仅仅是劳动力与资本，至少还有土地投入等等。为了克服模型的不完美，学者们一直不懈进取，通过各种方法不断拓展、改进该模型，站在柯布——道格拉斯的“肩膀”上，SOLOW R·W·和SWAN T·W·（1956）提出了新古典经济增长模型，MEADE J·E·等学者于1961年就提出了在资本和劳动两解释变量之外另外再加进一个“土地成本投入”变量因素，同时还考虑了技术方面的影响因素，并且指出技术进步是一个“时序”变量，在此基础之上就有了SOLOW-SWAN模型。SOLOW-SWAN模型在理论上是乎没有什么破绽，但不能很好的解释实际相关问题，有时候甚至与实际情况出现相矛盾的情形。然而在1983年，ROMER P再次修正生产函数，在资本和劳动之外加上知识因素。

如上所述，对产出产生贡献的远不止资本和劳动因素。为了使模型更具说服力，先从理论上给予推理。首先，假定某经济系统由n个影响因素构成，简单地说就是有n个解释变量，并且每个解释变量Pi都对这个经济系统的产出均作出了一定的贡献，且它们的贡献也相应有一个测度值，把它记为Xi，由些可得如下方程形式：

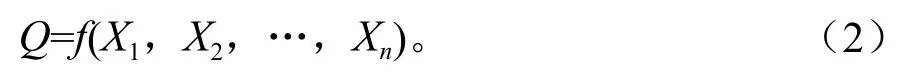
式中被解释变量Q表示该经济系统的产出，在具体的情况中可根据实际得出相应的产量、产出、产值或是收益等等。显然，这是模型的一般表达形式，其中，X1，X2，…，Xn表示各种要素的投入量，即通常所说的解释变量。它与生产方程模型（1）中的K，L是一致的，求全微分得：

两边同时除以Q，可得：

其中，

为弹性系数，当经济系统具有分形特征时，λi为常数，此时对式（5）两边求积分有：

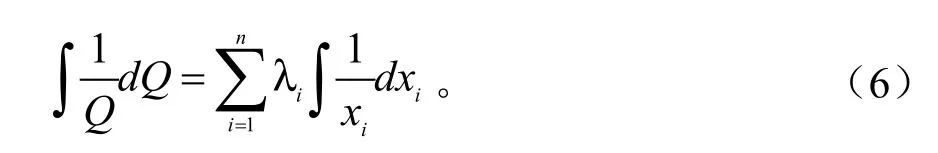
可转化为：

式（7）可称为经济系统的功能模型，其中A=expΣCi为比例系数，这里Ci为积分常数。当模型中只含劳动因素（L）、资本因素（K），式（7）便是典型的柯布——道格拉斯生产函数模型。

3.3 湘西州柑橘产出模型

根据前文解释变量设置可知，构建湘西州柑橘生产函数模型，被解释变量为湘西州柑橘产量，解释变量为对柑橘生产的系列影响因素。在此，将柑橘生产的影响因素分为：劳动力因素、科研经费因素、种植规模大小（以种植面积衡量）、劳动力素质因素（以学历衡量）、土地成本因素、化肥使用因素（以使用量衡量）、农药使用因素（以使用量衡量）以及其他影响因素的投入。

也即变量Xi(i=1，2，…，8)分别为：劳动力投入、科研经费投入、劳动力素质、土地投入、化肥使用投入量、农药使用投入量、其他影响因素投入量等。于是得如下模型：

以上模型为指数函数形式，计算比较困难，为了求解方便，对该模型进行数学处理，两边同时取自然对数，通过取自然对数这样的数学处理方法可将以上模型非线性形式转化为线性方程，得如下线性标准形式：

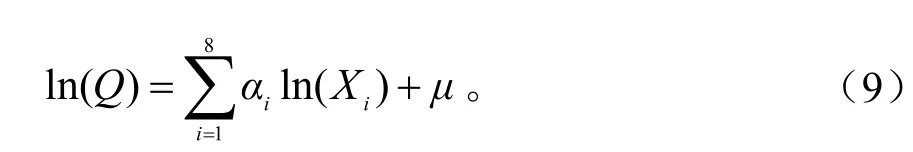
式中，μ是随机干扰项，为了确保函数模型参数估计量达到有效性、无偏性及一致性原则，在此对随机干扰项μ进行一定的假设：

①零均值假定，即E(μi)=0；

②同方差及无自相关性，D(μi)=σ2，Cov(μi，μj)=0；

③随机干扰项与解释变量不相关，Cov(Xji，μi)=0；

④μi～N(0，σ2)

为进一步把生产函数模型形式明了化，令Yi=ln(Xi)，则（9）式可化为：

3.4 数据说明

按照前文所设置的变量，采取分层抽样的方法对1995年至2014年30年湘西州柑橘种植情况进行抽样调查。数据格式见表2。

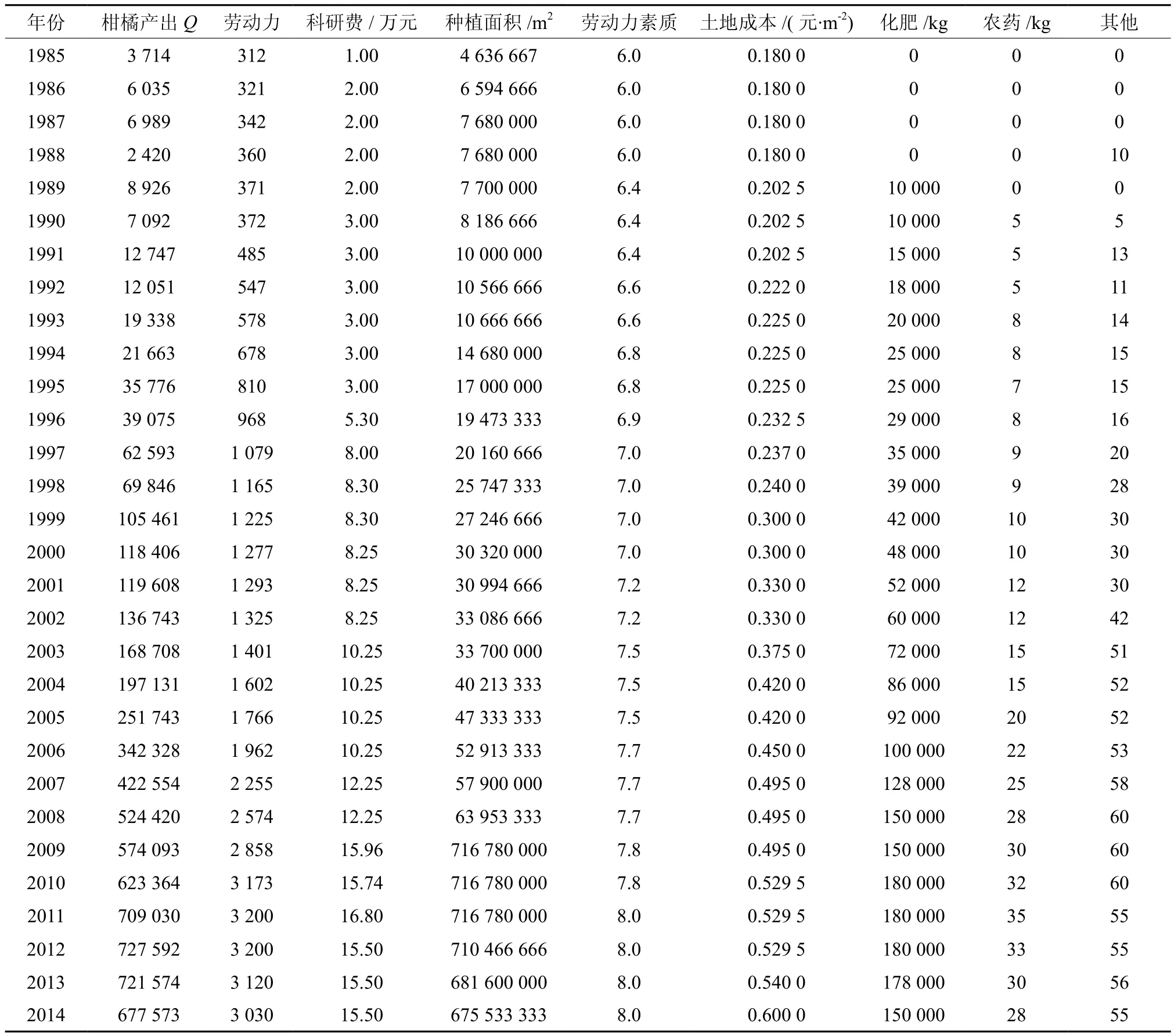
表2 柑橘产出及其影响因素调查†Table 2 Citrus yield and its influencing factors

由于以上生产函数模型是在原始模型上作了数学处理，即两边取了自然对数。而表2中的数据为原始数据，为使模型中数据具有合理性，对以上的原始数据也要进行一定的数学处理。同时，为了适合模型的古典假定，对表2数据中一些异常的、不存在普遍代表性的数据项给予删除。可得表3。

在接下来的部分中，将表3的数据代入以上生产函数模型，然后再应用普通最小二乘法(OLS)进行参数估计和显著性检验。

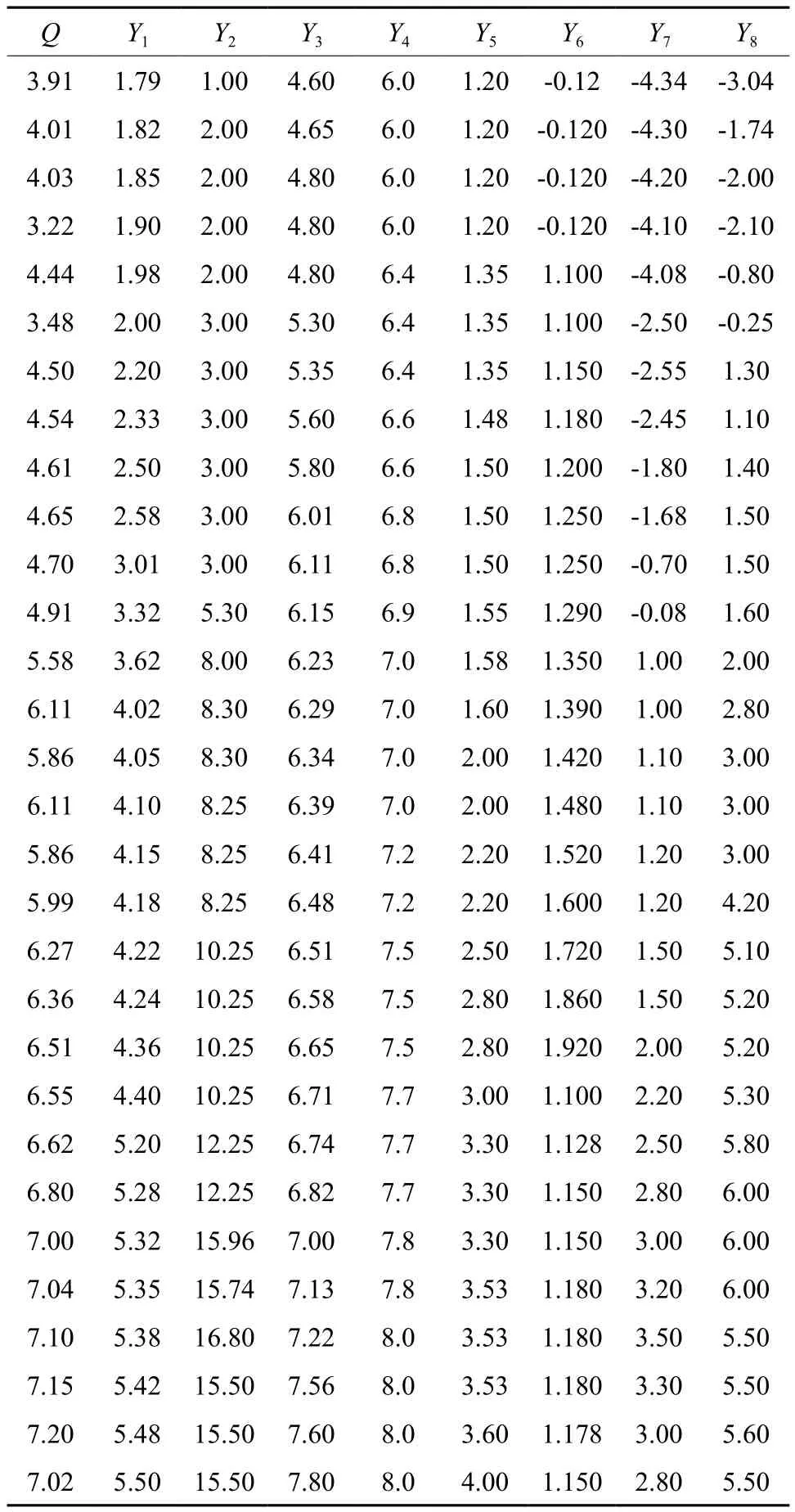
表3 柑橘产出及其影响因素数据处理Table 3 Data on citrus output and its influencing factors

3.5 柑橘产出模型的估计

在参数估计方面，应用了SPSS17.0软件、对表3的数据进行估计，结果如下（见表4）：

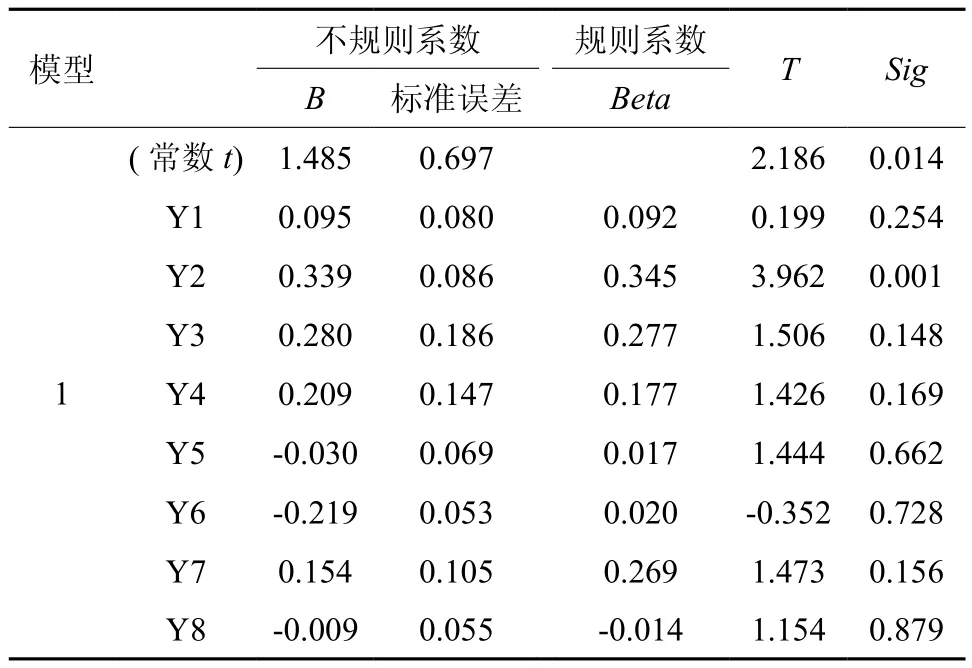
表4 柑橘产出模型的分析†Table 4 Analysis of citrus output model

从模型结果来看，模型整体效果很好，F值为407.343，R-squared为0.921，也就是说，本模型能准确反应真实情况的概率为92.1%，Sig值小于0.05，在显著性水平为5%以下时，具有显著影响，各影响因素之无自相关现象。通过软件输出结果图表，可见，该生产函数模型满足OLS的古典假定，由此得知该模型的结果是可靠的。从软件输出结果表可知该函数模型的线性回归形式为：

=0.092 7Y1+0.345Y2+0.027Y3+0.177Y4+0.260Y5+0.269Y6-0.014Y7+0.142Y8，从软件输出结果表可知各参数T检验值分别为：0.199、3.926、1.500、1.444、-0.352、1.154 和 0.377。

3.6 模型估计结果分析

本函数生产模型中被解释变量Q对解释变量Yi（i=1，2，…，8）的回归非标准化系数，即各个参数估计值分别为0.092、0.345、0.277、0.177、0.017、0.02、0.014及0.142，其对应的显著性检验 的t值 分 别 为 0.199、3.962、1.506、1.426、1.444、-0.352、1.473、1.154其 中， 而Y1、Y2、Y3、Y4、Y5和Y6的回归系数B值分别为：0.095、0.339、0.280、0.209、-0.3、-0.219、0.154 及-0.009。在显著性水平0.05情况下，可以认为解释变量Y2、Y3、Y4、Y6、Y7对被解释变量Q有显著影响，而Y1、Y5和Y8的B值绝对值大于0.05，接受原假设，认为这3个解释变量对被解释变量无显著性影响。计量结果表明柑橘科研经费的投入量Y2、柑橘种植面积规模Y3、劳动力素质指数Y4、化学肥料投入量Y6以及对柑橘进行多少农药喷撒量Y7对柑橘的生产具有有显著性影响，其他的影响因素并不显著。该函数模型看似与实际情况有些不相符，表现在柑橘的产量与劳动力关联不大这个问题上。为什么劳动力在柑橘生产函数模型上不显著呢？主要是因为：柑橘产业只是在某些环节上属于劳动密集型产业，但不是任何环节都需要大量的劳动力，大量劳动力的投入对柑橘产出的影响就很小。同时，从劳动力综合素质指数Y4对柑橘生产的影响呈显著性，可以看出在柑橘生产过程中，劳动力的数量并不是柑橘产出的决定性因素，而劳动力的综合素质才会对柑橘种植大规模产出起着关键性作用。第二、解释变量土地投入Y5对柑橘生产的影响也表现出不显著性，其原因在于湘西自治州当前土地使用的成本很低，柑橘的产出价值相对土地使用成本来说，可以使土地成本忽略不计。其他投入量在柑橘正常生产过程中不一定进行投入，可作为随机扰动项处理，其投入存在着随机性，并不是任何时候都需要进行投入的。因此，对柑橘生产的影响表现出不显著性是正常现象。

3.7 柑橘生产函数模型的修正

从上面函数生产模型中可知，由于Y1、Y5和Y8对被解释变量Q无显著性影响，因此，可将这3个无显著性影响的解释变量进行剔除，从而达对上述模型进行修正的目的，再次运用Spss软件对柑橘产出总量Q与科研经费影响因素投入量Y2、种植面积规模影响因素Y3、劳动力素质指数因素Y4、化学肥料投入量Y6、农药投入量Y7进行计算，结果如下（见表5）：

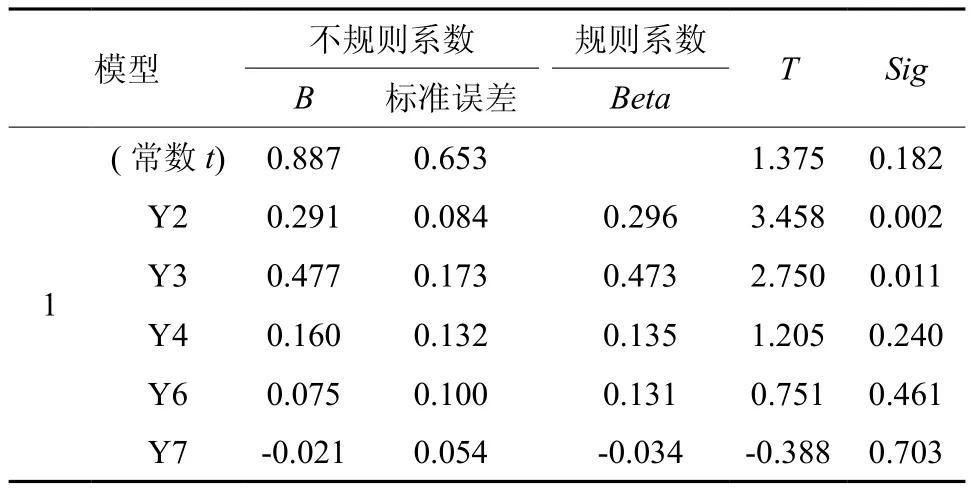
表5 柑橘产出修正模型的分析†Table 5 Analysis of citrus output correction model

得修正的线性回归模型为：

=0.296Y2+0.473Y3+0.135Y4+0.003Y5+0.131Y7-0.034Y8。

4 结论与讨论

l）科研经费的投入对柑橘产出的弹性系数为0.296，表明对柑橘进行科研经费投入的多少对柑橘产出呈边际递增的影响，该影响因素的B值为0.291，可见该影响因素的影响程度具有显著性，这不仅与修正之前情形相符合，还与实际情况相一致。弹性系数为0.296说明，在其他影响因素不变的前提下，对柑橘的科研经费每增加一个百分点，柑橘的产量将增加0.296%。这些数据也说明湘西自治州柑橘与国际柑橘相比，湘西自治州柑橘科研经费投入较少是造成湘西自治州柑橘竞争力较弱的一个原因。

2）柑橘种植的规模对柑橘产出的弹性系数为0.473，表明除这种植规模之外，在其他影响因素不变的前提下，种植面积每扩大一个百分点，柑橘产出就会增加0.473%，这个数据足以说明柑橘还是个附加值较高的产品，也就是说消费者在购买柑橘时，不仅会考虑柑橘的质量、价格等直观性因素，还会受到柑橘无形品牌的影响。一般种植规模越大，其柑橘果实品质就会越高，同时品牌的知名度就越响亮，这不仅符合规模效益原理，也符合市场发展规律。说明湘西柑橘还应该进行资源整合，提升规模效益、完善湘西柑橘的行业集中度。

3）劳动力素质影响因素指数对柑橘产出的弹性系数为0.135，根据弹性系数的含义可知在其他相关影响因素不变的前提下，劳动力素质指数每增加一个百分点，柑橘产出量就会增加0.135%，从这个数据可知柑橘生产是个具有科技含量的农产品，柑橘科研人员的素质越高、科研力量越强，柑橘在市场的竞争中就会越有优势。

4）影响化学肥料投入量参数估计值为0.131，即对柑橘产出的弹性系数是0.131，根据弹性系数的含义可知在其他相关影响因素不变的前提下，说明化肥投入每增加一个百分点，柑橘的产出量就会增加0.131%，这数据还说明柑橘是个需要肥料的农作物，合理有效的投入化肥的用量对柑橘的生产具有积极作用。但是化肥的投入量不能过度投入，过度投入会造成土壤环境的破坏，反而会负面影响柑橘的产出。

6）影响农药投入量的参数估计值为-0.034，根据弹性系数的含义可知在其他相关影响因素不变的前提下，农药投入每增加一个百分点，柑橘的产出就会下降0.034%。这告诫我们，在柑橘生产过程中，若田间管理不妥，容易使柑橘受到病虫危害。

[1]曾柏全,邓子牛,杨迎花 ,等. 湖南宽皮柑橘SRAP的反应体系[J].中南林业科技大学学报,2008,28(6):71-74

[2]白 婕,李 娟,张 靖.金橘果渣膳食纤维制备工艺研究[J].中南林业科技大学学报,2009,29(3):118-120.

[3]熊 巍,祁春节. 湖北省柑橘产业生产效率的DEA分析[J].华中农业大学学报(社会科学版),2012(5):36-40

[4]张炳亮.我国柑橘产业投入产出效率测算、趋势及改进[J].广东农业科学, 2014 , 41(14):219-223.

[5]宋金田,祁春节.农户柑橘种植意愿及影响因素实证分析[J].华中农业大学学报(社会科学版), 2012(4):17-21.

[6]汤荣丽.我国柑橘投入产出效率研究[D].杨凌:西北农林科技大学,2012.

[7]栾好安.三峡库区橘园绿肥的生态效应及其对柑橘产量和品质的影响[D].武汉:华中农业大学,2015.

[8]钟 冰,陈远喜.施氮量对柑橘产量·品质·经济效益的影响[J].安徽农业科学, 2016 , 44 (36):74-76.

[9]张建春.柑橘产量和品质的影响因素及应对措施[J].中国园艺文摘,2012 , 28(1):151-152

[10]彭湘莲, 付红军.湖南省食品安全问题与对策建议[J].中南林业科技大学学报(社会科学版), 2014, 8(6): 67-70.