特高压线路对对空情报雷达探测干扰的研究
杨嘉炜 唐 波 黄 力 郝 斌
(三峡大学 电气与新能源学院, 湖北 宜昌 443002)
随着我国特高压线路和雷达站的建设日益增多[1-2],这两种间距以公里为单位的行业级系统之间电磁干扰问题日益严重[3].然而,当前工程中所应用的《对空情报雷达站电磁环境防护要求》标准规范,仅针对500 kV及以下电压等级的输电线路和对空情报雷达站的防护间距进行了规定,而对于当前以特高压线路为骨干的电网建设,缺乏用于指导相应工程建设的防护标准.虽然没有给出特高压线路与对空情报雷达站之间的防护间距,但文献[4]提出了对空情报雷达站的防护准则.该准则包含3个方面的要求,分别对雷达站周边环境的允许最大干扰电压、允许最大探测距离损失和允许持续干扰时间做出了规定.对于允许最大干扰电压,其最低限值可以通过给出的公式计算得出;对于允许最大探测距离损失,规定中只给出了其最低限值,没有给出具体的求解方法;对于允许持续干扰时间,则属于工程实际中出现的非可控因素.因此,研究特高压输电线路对对空雷达站的防护问题,难点在于探测距离损失的求解.
目前,国内外还鲜有特高压输电线路对对空雷达站探测干扰的研究,仅文献[5]以模型实验的方法研究了特高压线路对雷达电磁波的衰减效应.但实验频段单一,与实际环境存在差异,无法真实反映干扰损失的实际情况.不过,在输电线路无源干扰的理论分析与数值求解方面[6-7],现有研究成果较多,可以进行参考.如针对雷达所处的甚高频频段,现有无源干扰高频的计算通常采用PO算法.PO算法是一种用于求解电大尺寸物体电磁散射数据的高频近似算法,以计算速度快、占用资源少的特点为研究人员广泛应用[8].但是,由于PO算法在计算时忽略了目标物体边缘绕射场的贡献,使得在求解如特高压铁塔这类复杂目标物体的电磁散射问题时精度欠佳[9],因此在进行较高精度求解时,需要对算法进行改进.
为准确数学表征探测距离损失,本文以文献[4]规定的干扰防护准则为研究依据,结合雷达回波公式,提出一种基于特高压输电铁塔雷达散射截面求解探测距离损失的思想.在此基础上,从雷达电磁波入射和铁塔模型的角度出发分析,研究了将ILDC法与PO法相结合应用于求解输电铁塔散射场的条件与耦合方式,实现了探测距离损失的快速准确求解.
1 对空雷达站的干扰问题及其防护准则分析
1.1 特高压输电线路对雷达站的干扰机理
特高压输电线路在电磁波激励下体现为一种极电大尺寸的电磁强散射体[10].如图1所示,当线路临近雷达站时,由于线路对入射的雷达电磁波造成散射,从而造成原雷达电磁波的幅值及相位变化,形成干扰.
现有输电线路无源干扰研究表明[11],在雷达入射波垂直极化条件下,由于线路铁塔垂直于地面,而导线与地面平行排列,因此,干扰的主要来源为铁塔,而导线造成的干扰权重则通常予以忽略.基于此,本文仅对特高压铁塔的干扰进行研究.

图1 输电线路铁塔对雷达探测干扰示意图
1.2 对空情报雷达干扰防护准则分析
国家标准《对空情报雷达站电磁环境防护要求》明确提出了3条防护准则:1)有源干扰不可避免的情况下,探测距离损失不得超过5%;2)电磁障碍物对雷达探测距离影响损失不超过5%;3)一次连续干扰时间不超过10 s,两次干扰时间间隔不少于10 s,每小时干扰时间不超过工作时间的5%.
对于防护准则(1),防护标准对雷达站周边的不同设施规定了与其对应的电压限值来进行评定,因此对于高压架空输电线路,可以用其给出的公式进行干扰电压计算:
Ujfmax=0.48CUnf
(1)
式中,Ujfmax是雷达接收机输入端最大容许干扰电压有效值,单位为μV;C是相对于白噪声最大容许干扰电压增量系数,在高压架空输电线路中取值为3;Unf是等效到接收机输入端的系统噪声电压有效值,单位为μV,根据雷达站的工作频率80~300 MHz取值为0.77 μV.
计算可得,特高压线路对雷达站的干扰电压应小于等于1.1 μV.对于防护准则(3)允许持续干扰时间,这属于工程实际中出现的不可控因素,本文不做过多讨论.防护准则(2)中的探测距离损失问题,是本文研究的重点.
2 雷达探测距离损失的分析求解
2.1 雷达站探测距离损失的评估方法
根据文献[12],在雷达发射探测功率不变的情况下,允许探测距离5%的损失可以等效为雷达探测功率降低0.9 dB.
假设雷达发射功率为Pt,发射天线增益为Gt,接收天线增益为Gr,λ为雷达波长.当雷达距离目标为R时,雷达波功率大小Pr可以表示为[13]:
(2)
式中,σ为目标的RCS,L为系统传播损耗.
研究雷达功率时,通常以分贝(dB)进行描述,其对应的计算公式为10lg(A/B),其中A和B是两个需要比较的数值.因此,雷达探测功率损耗可以表示为:
ΔP=10lg(Pr/Pt)
(3)
将式(2)带入式(3)后可以看出,影响雷达探测功率损耗的主要变量仍是σ,如发射功率、波长、天线增益等参量取决于雷达的自身属性,因此将σ作为求解输电线路铁塔对雷达探测功率损耗的重要中间参量,RCS的求解成为解决雷达探测损耗的关键问题.
2.2 RCS及其PO算法求解
文献[14]给出了RCS的求解公式:
(4)
式中,Es为输电线路散射场,Ei为入射波场强,R为雷达离目标的距离.


图2 输电线路铁塔RCS求解的数学模型
在高频电磁散射计算问题当中,通常采用高频近似算法进行散射场求解[15],其中应用最为广泛的是PO法.PO法是基于Stratton-Chu散射场积分方程展开的.根据铁塔角钢结构,铁塔的电场积分方程可以表示为:
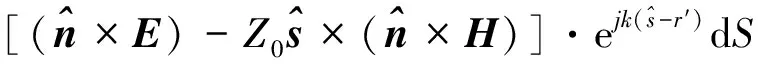
(5)

如图3所示,根据雷达入射波照射方位对铁塔角钢进行明暗区域划分,同时由PO法适用条件可知,在求解铁塔表面感应电流积分时需满足以下条件:1)铁塔表面曲率半径远大于电磁波波长;2)铁塔照明区存在感应电流,其阴影区感应电流近似为零;3)铁塔照明区表面上的感应电流特性与入射点表面相切的无穷大表面上的感应电流特性相同.
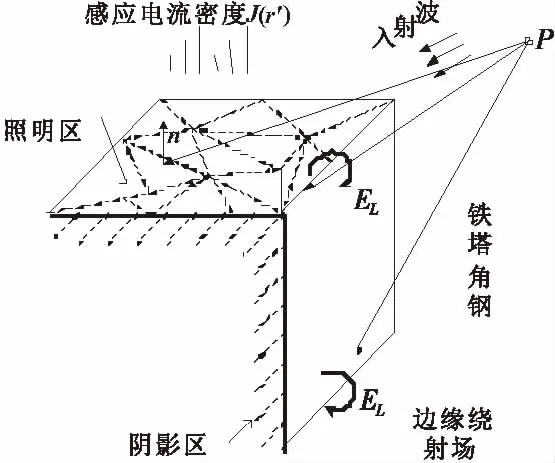
图3 角钢散射场
当雷达入射电磁波照射到铁塔时,由于铁塔角钢的“∟”型结构,入射波在角钢凹口处会形成较大的阴影区域.如图3所示将角钢面划分为照明区、阴影区以及角钢边缘的过渡区.物理光学法(PO)是对角钢表面照明区域的感应电流积分,将阴影区域感应电流近似为零,忽略了角钢边缘绕射场的贡献,因此在仅运用PO法求解铁塔散射场时精度欠佳.为此,本文引入增量长度绕射系数法(ILDC)对角钢边缘绕射场进行修正,提高计算精度.
3 运用PO-ILDC法求解RCS与功率损耗
3.1 应用PO法求解散射场
根据式(5)电场积分方程,其中旋度矢量可以用感应电流密度矢量表示[16]:
(6)
式中,系数δi是考虑遮挡效应的影响,当观察点位于阴影区时,δi=0;在照明区时,δi=±1,它的符号由入射角和表面法矢量的关系决定.
将式(6)带入式(5)后看出,PO法实质上是将铁塔的散射场表示成关于铁塔表面感应电流的函数积分式,而铁塔表面的感应电流密度为方程的未知数.因此,只要求出感应电流分布,就可以通过简化后的电场积分方程求解铁塔的散射场.
为求解表面感应电流积分,需要对角钢表面进行剖分,将铁塔表面划分成许多小的三角区域[17]:
(7)
式中,Λn(r)为已知的RWG基函数[18];N为整个铁塔模型剖分后,三角面元对公共边的总边数;γn为待求的标量系数.

(8)
式中,k=1,2,……,N.

图4 角钢三角面元对

(9)
将式(9)带入式(7)即可以求出铁塔表面感应电流,然后根据式(5)对感应电流函数进行积分,就可以求出铁塔照明区的散射场.
3.2 应用ILDC法求解角钢边缘绕射场
增量长度绕射系数法(ILDC)基于物理绕射理论(PTD),并在此基础上做出了修正,求得了观察点位于任何方向的绕射系数.Mitzner认为任何形状的边缘散射场可以通过对其照射部分的积分来求得,并将其结果集中于增量形式[19].因此,铁塔边缘绕射场贡献可以表示为:
(10)
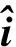
(11)
利用ILDC法进行计算时,需要考虑角钢边缘处与PO法的耦合,图5为当雷达入射波以不同角度照射在角钢劈面上的模拟示意图,φi和φs分别为入射和绕射方向的横向分量与角钢的一个劈面夹角,n为对π归一化外劈角.为避免因重复计算导致散射场叠加.在绕射系数展开项中的引入一个阶跃函数:
(12)

图5 角钢入射波夹角图
阶跃函数的作用是根据给定角钢的劈面而言的,雷达入射波投到一个劈面时,应加上物理光学项,另一劈面没被照射到时,则应去掉对应物理光学项.同时,在目标边缘处,ILDC法还加入了对绕射系数的修正项,以提高计算精度.文献[20]推导并展开了并矢量绕射系数的各项参数,本文这里不过多叙述.
3.3 RCS与功率损耗的求解
(13)
将计算结果Es带入式(4)求出铁塔的RCS,然后,将RCS结果带入式(2)和式(3)即可计算出铁塔对雷达探测功率的损耗.
3.4 基于简单模型的算例验证
为验证PO-ILDC法的准确性,通过以矩量法(MOM)为基准,并采用特高压铁塔角钢模型进行算例验证.矩量法是一种离散积分方程的数值方法,其计算精度较高,但在计算复杂目标的高频电磁散射问题时耗费资源过大,因此只建立简单模型进行验证.
根据特高压工程实际,按照角钢规格L200建立角钢模型图6(a)和1基铁塔模型图6(b).
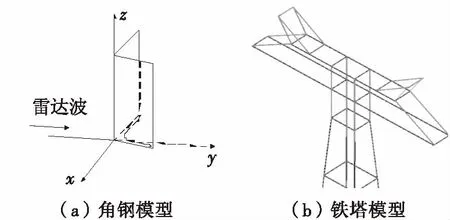
图6 简单模型
模型中角钢宽度为0.2 m,雷达激励源采用垂直极化平面波入射,电场强度为1 V/m,入射频率变化范围80~300 MHz,设置101个频点,通过和PO法、MOM法对比进行分析.
如图7是以矩量法(MOM)为基准的3种算法计算结果对比.从图中可以看出,采用PO法计算角钢的RCS时,计算结果相对于MOM法偏差较大,原因是采用PO法计算电场时忽略了角钢阴影部分感应电流,导致结果偏低.相比之下,采用PO-ILDC法的计算结果和MOM法基本吻合.

图7 PO法和PO+ILDC法RCS求解对比(角钢)
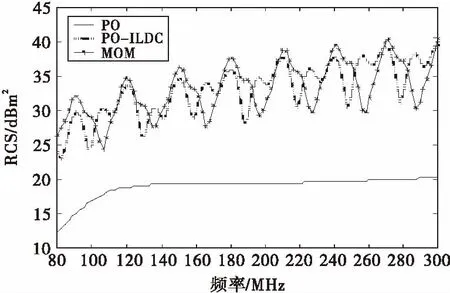
图8 PO法和PO-ILDC法对比结果(铁塔)
为保证算法在复杂目标结构计算中的精度,采用如图6(b)所示与实际特高压铁塔相近的塔型进行建模,该模型中铁塔总高65 m,横担宽35 m.
从图8中可以看出,采用PO法计算的1基铁塔RCS结果明显低于MOM法和PO-ILDC法,相比之下,PO-ILDC法和MOM法结果吻合较好,验证了新算法的稳定性.
4 雷达探测功率损耗的仿真计算
在特高压线路的干扰研究中,通常采用5基铁塔作为研究对象[21],而此时矩量法不再适用.利用PO-ILDC的结合算法分别求解了80 MHz、200 MHz、300 MHz频率下5基铁塔对雷达的功率损耗随防护间距的变化情况,如图9所示.
从图9可以看出,3种不同频率激励下的铁塔对雷达造成的功率损耗均在2.6 dB以内;并且随着频率的提升,损耗幅值也不同程度上增大;同时,随着雷达和铁塔之间距离的加大,在2.2 km后,不同频率下的损耗都下降至0.9 dB内.图9中虚线表示的是标准规定的损耗限值0.9 dB.结合图示来看,当雷达入射频率为80 MHz时,损耗最大值约为1.5 dB,随着间距距离提升至1.6 km,损耗降低到了规定限值;当入射频率为200 MHz时,最大损耗约为2 dB,且当间距达到2.1 km后,损耗下降至0.9 dB;最后当频率提升到300 MHz后,防护间距需要到2.3 km才可以符合标准规定.

图9 雷达探测功率损耗
5 结 论
1)相比于应用模型实验测量雷达探测功率损耗,本文提出的基于RCS的探测功率损耗求解方法在一定程度上节省了人力资源和经济成本.同时,本文提出的利用ILDC法与PO法相结合的方式求解特高压输电铁塔的电磁散射问题奠定了理论基础.
2)根据防护准则和研究结果,对空雷达站周边干扰电压不允许超过1.1 μV,而出现干扰时,持续干扰时间应尽量控制在10 s以内.当特高压工程建设邻近对空雷达站时,根据最大频率下的干扰损耗,应距离雷达站2 200 m以外进行线路规划.
[1] 刘振亚.特高压电网[M].北京:中国经济出版社,2005.
[2] 刘振亚,张启平,董 存,等.通过特高压直流实现大型能源基地风、光、火电力大规模高效安全外送研究[J].中国电机工程学报,2014,34(16):2513-2522.
[3] 邬 雄,万保权.输变电工程的电磁环境[M].北京:中国电力出版社,2009:83-94.
[4] 国家技术监督局.GB13618-92.对空情报雷达站电磁环境防护要求[S].北京:中国标准出版社,1992.
[5] 陈京平,刘建平,田军生.特高压输电线路线塔对电磁波的衰减效应试验研究[J].现代电子技术,2008(15):146-148.
[6] Toyada S, Hashimoto H. Scattering Characteristics of VHF Television Broadcasting Waves by Steel Towers of Overhead Power Transmission Lines[J]. IEEE Transactions on Electromagnetic Compatibility,1979,21(1):62-65.
[7] Zhang Xiaowu, Tang Jian, Zhang Huanguo, et al.Reradiation Interference Computation Model of High Voltage Transmission Line to the Shortwave Radio Direction Finding Station[C]. 20th International Zurich Symposium on Electromagnetic Compatibility, Zurich, Switzerland: IEEE Electromagnetic Compatibility, 2009:309-312.
[8] 方全杰. 物理光学法在导体与涂层目标电磁散射中的应用[D].西安:西安电子科技大学,2011.
[9] 朱艳菊,江月松,张崇辉,等 应用改进的物理光学法和图形计算电磁学近似算法快速计算导体目标电磁散射特性[J]. 物理学报,2014,63(16):182-188.
[10] 唐 波. 特高压直流线路对邻近无线电子设施电磁干扰防护的关键问题[D].武汉:华中科技大学,2011.
[11] 赵志斌,干喆渊,张小武,等. 短波频段内UHV输电线路对无线电台站的无源干扰[J]. 高电压技术,2009,35(8):1818-1823.
[12] 刘洋涛,郝志梅. 对单脉冲雷达角度跟踪系统的干扰仿真研究[J]. 航天电子对抗,2012,28(4):62-64.
[13] 丁鹭飞,耿富录,陈建春. 雷达原理[M].北京:电子工业出版社,2014.
[14] Chen V C, Ling H. Time-Frequency Transforms for Radar Imaging and Signal Analysis[M].Boston: Artech House, 2002.
[15] 陈毅乔. 电大尺寸目标的电磁特性分析方法研究[D].成都:电子科技大学,2008.
[16] 田德元. 矩量法和物理光学法的混合算法及应用研究[D].西安:西安电子科技大学,2012.
[17] Jakobus U,Landstorfer F M. Improved PO-MoM Hybrid Formulation for Scattering from Three Dimensional Perfectly Conducting Bodies of Arbitrary Shape[J]. IEEE Trans. On Antennas and Propagat.,1995,43(1):162-169.
[18] Taboada J, Obelleiro F, Rodriguez J, et aI. Incorporation of Linear-Phase Progression in RWG Basis Functions[J]. Microwave and Optical Technology Letters, 2005, 44(2):106-112.
[19] Mitzner K M. Incremental Length Diffraction Coefficients,TechnicalReportNo.AFAL-TR-73-296[R]. NorthropCorporation,AircaftDivision,April 1974.
[20] Michaeli. Equivalent Currents for Arbitray Aspects of observation[J].IEEE Trans.Antennas and propagation, 1984, Ap-32(3):252-258.
[21] 唐 波,文远芳,张小武,等. 中短波段输电线路无源干扰防护间距求解的关键问题[J]. 中国电机工程学报,2011,31(19): 129-137.

