基于EWT和SVD技术的齿轮故障诊断方法研究
陈保家 刘浩涛 聂 凯 汪新波 邱光银
(1. 三峡大学 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002;2. 三峡大学 机械与动力学院, 湖北 宜昌 443002)
齿轮作为引发机械故障的重要部件,其故障诊断方法一直以来都是相关行业的研究热点.齿轮发生故障时,其振动信号往往呈现出非线性、非平稳等特点,如何从齿轮故障信号中提取故障特征是齿轮故障诊断的关键.在处理齿轮振动信号处理时,FFT能分别统计信号的时、频域平均结果,但无法同时兼顾信号的时、频域特征.小波分析具有多尺度特性,能同时提供信号的时、频局部化信息,但是由于其也是在傅里叶变换的的基础上发展得到的,这使得其在非平稳信号分析过程中存在虚假信号及假频等诸多问题[1].此外,小波基函数数量较多,当选用的小波基函数不同时,小波分解的结果也会大相径庭,因此为了获得最适合的小波基就需要对不同的小波基函数进行尝试,从而限制了小波变换的应用.基于上述信号处理方法的缺点,经验模态分解(EMD,Empirical mode decomposition)方法应运而生,它摒弃基函数的概念,摆脱了传统傅里叶变换算法的束缚,依据信号自身特征对信号进行分解,具有良好的自适应性和时频聚焦性,并且在机械故障诊断方面获得了广泛的运用.但是EMD是一种经验性的方法,缺乏完备的理论基础,利用EMD方法分解得到的IMF分量也无法在理论上证明其正交性.并且由于过包络,欠包络等问题使得EMD对信号进行分解时容易出现模态混叠现象[2].
针对EMD方法缺乏理论依据等诸多问题,Gilles于2013年提出了一种新的的信号处理方法,即经验小波变换(empirical wavelet transform,EWT)方法.它是结合EMD的特点,在小波分析的理论框架上建立起来的.该方法主要思路是:先按照一定的划分方式来划分信号的傅里叶频谱,然后自主建立滤波器组对划分后的频谱进行滤波从而获得一系列有紧支撑的调幅-调频分量.本文将EWT方法与奇异值分解(singular value decomposition,SVD)技术相结合,提出了一种齿轮故障种类识别方法.
1 EWT方法
在EWT对信号进行分解的过程中,一般规定信号傅里叶频谱的频率范围为[0,π],在原始的EWT分解方法中,假设信号由N个单分量成分组成,找到频谱图中的极大值,如果极大值个数为M,将这些极大值降序排列,则存在两种情况[3-4]:
1)M≥N,此时算法找到了足够的极大值,保留前N个极大值;
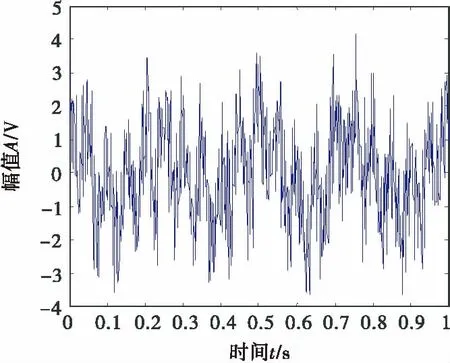
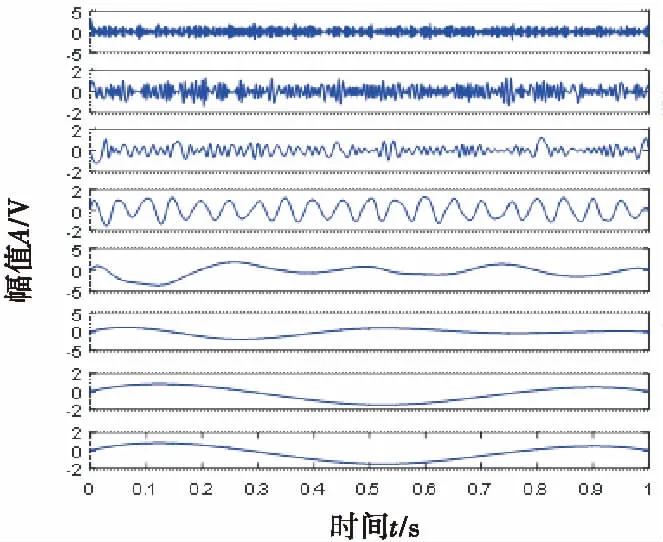
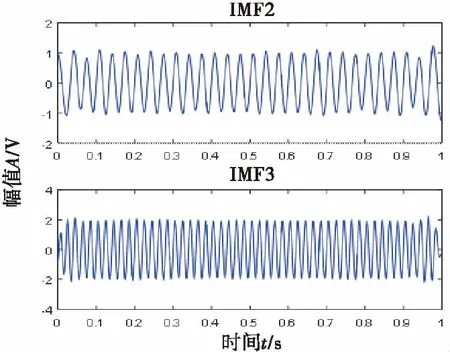
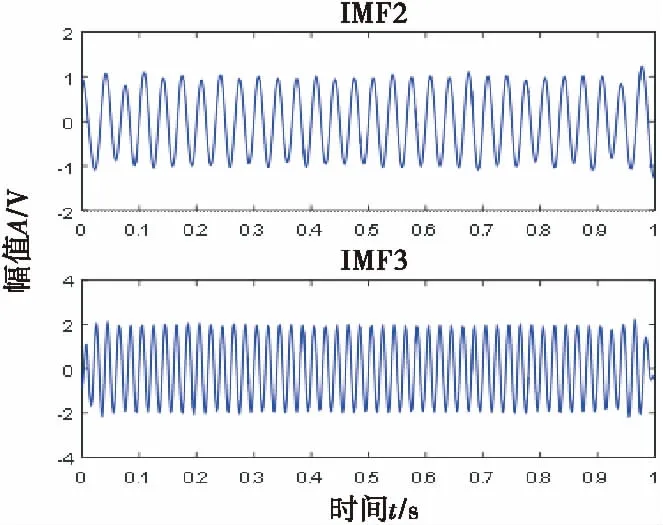
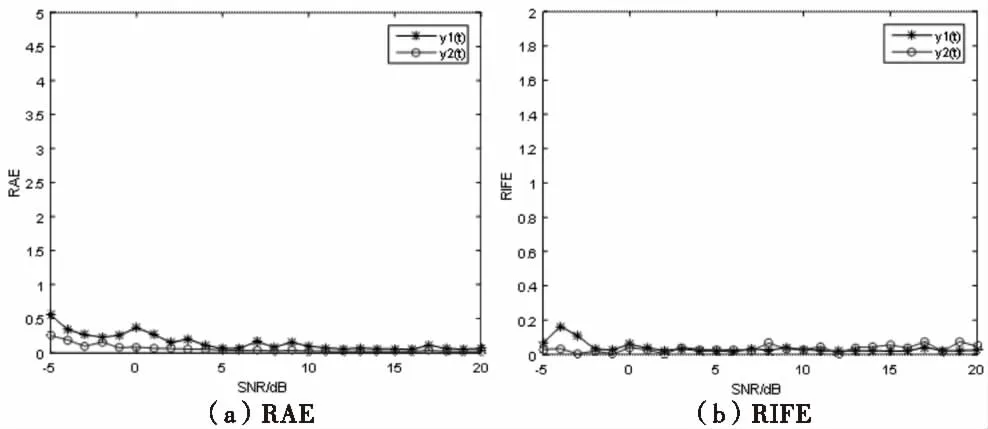
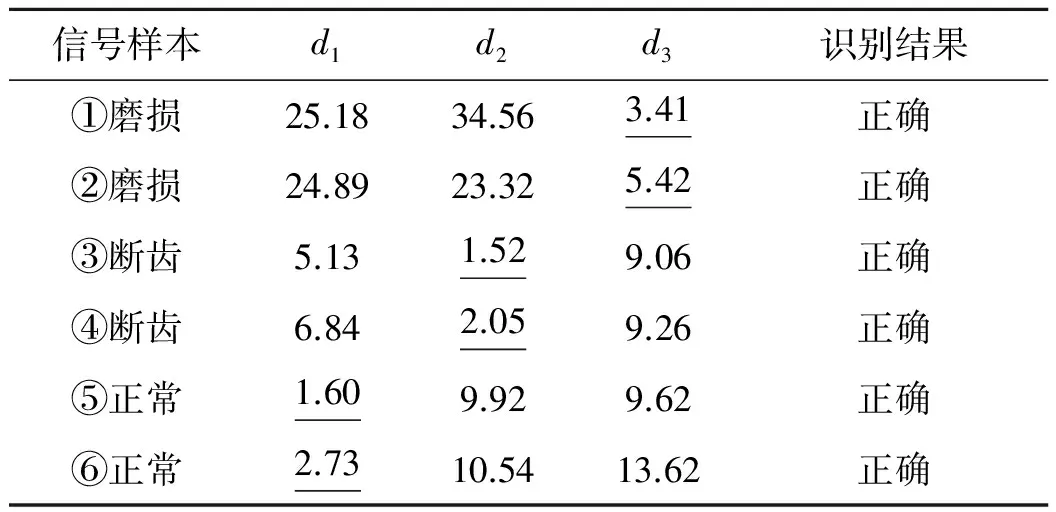
2)M 图1 傅里叶坐标系分割图 在确定分割区间式后,对其加小波窗,根据Meyer小波的构造方法,定义经验尺度函数和经验. 小波函数分别为: (1) (2) 其中,γ 根据经典小波变换的构造方法构造经验小波变换,细节系数和近似系数分别为: (3) (4) 进行信号重构的结果如式(5)所示. (5) 由以上公式得到经验模态函数fk,可由式(6)和(7)表示: (6) (7) 下面利用仿真信号x(t)=x1(t)+x2(t)+x3(t),对EWT和EMD的分解效果进行对比,其中各分量分别为x1(t)=cos(8πt)、x2(t)=cos(40πt),x3(t)为高斯白噪声,信噪比为0.4,混合信号x(t)的波形如图2所示. 图2 混合信号x(t)的时域波形 对信号x(t)分别进行EMD变换和EWT变换,分解结果如图3~4所示.图3中,信号经过EMD分解后的分量达7个之多,有明显的模式混叠现象,并且只有分量x1(t)=cos(40πt)被分离出来.而图4中,混合信号经过EWT分解后,x(t)的单分量x1(t),x2(t)被准确地分离出来,可见EWT的分解效果要明显优于EMD. 图3 x(t)的EMD变换 图4 x(t)的EWT变换 由于在数据样本的采集过程中可能产生干扰噪声,为了研究EWT方法对噪声的鲁棒性,本文将对合成信号z(t)=y1(t)+y2(t)+n(t)进行分析.其中y1(t)=sin(2πf1t)、y2(t)=2sin(2πf2t)(f1=30 Hz,f2=50 Hz),n(t)为高斯白噪声,信噪比为SNR. 当SNR=20dB时,信号z(t)经过EWT变换总共获得12个IMF分量,为了便于研究,只取分量IMF2和IMF3,如图5所示.IMF2和IMF3对应于信号y1(t)和y2(t),从图中可以看出两者的幅值误差很小,分解的效果非常理想. 图5 通过EWT变换得到的对应IMF(SNR=20 dB) 当SNR=1 dB时,z(t)被分解为13个IMF分量,同上,只取y1(t)和y2(t)所在的分量IMF2和IMF3,如图6所示. 图6 通过EWT变换得到的对应IMF(SNR=1 dB) 随着信噪比强度的增加,两者间的幅值误差相比于SNR=20 dB有了明显的增大.为了评估y1(t)和y2(t)与其对应的IMF分量之间的幅度误差和瞬时频率误差,如下定义了两个误差测度指标: (8) (9) 式中,RAEi和RIFEi分别表示yi(t)与其对应的IMF之间的相对幅度误差,相对瞬时频率误差.n是采样点的序列号,i=1,2,下标j是IMF的序列号,fi(n)为对应yi(t)的瞬时频率,IFj为对应IMFj的瞬时频率. 在不同的SNR下计算这两个误差测度指标,如图7所示.从图7(a)可以看出虽然RAE随着SNR的增强逐渐增大,但误差始终保持着较小值,小误差表示z(t)的单分量已经被精确地分离出来.图7(b)中,RIFE具有相似的变化趋势,且噪声水平对其影响更小,证明了EWT对噪声的鲁棒性较强. 图7 不同SNR下的误差测度 利用EWT方法对齿轮振动信号x(t)进行分解,得到的n个IMF分量C1,C2,…,Cn,它们分别包含了不同的频率成分,由于不同故障信息所在的频率段各不相同,因此将这n个IMF分量按不同频率带分成若干组来组成初始向量矩阵[6].由于EWT分解得到的分量是从低频到高频的,本文为了叙述方便,先将n个进行倒序处理,将其组成初始向量矩阵A: A=[CnCn-1…C1] (10) 由矩阵理论可知矩阵的SVD有三大固有特性:其一是它具有较好的稳定性,即当矩阵元素发生微小的变化时,对其奇异值的影响很小;其二是比例不变性,即当矩阵进行比例缩放后,其奇异值也同等缩放,变化的只是奇异值的大小,奇异值的变化趋势依然不变[7].其三是旋转不变性,也就是矩阵和矩阵的转置具有相同的奇异值,这些特点使得奇异值能有效地描述初始向量矩阵A的特征. 图8所示为齿轮故障诊断方法流程图,在用EWT方法对原始信号进行分解并形成初始向量矩阵A后对矩阵A进行奇异值分解,将分解后的奇异值作为识别齿轮故障诊断的特征向量,识别的方法是马氏距离判别函数[8]. 基于EWT和奇异值分解技术的齿轮故障诊断的具体步骤如下: 1)分别在齿轮正常、断齿和磨损故障状态下按一定的采样频率进行采样; 2)对每个振动信号进行EWT分解,获得若干个IMF分量; 3)根据式(11)利用分解得到的IMF分量形成初始向量矩阵A,并对其进行奇异值分解,求出奇异值σA,j: (11) 依据奇异值分解特性可知数列σA,j中元素呈依次递减,j=1,2,3分别代表正常,断齿,磨损状态. (12) 5)在训练样本以外的待检振动信号中随机取一振动信号作为被诊断信号并进行EWT分解,然后依照上述方法获得被诊断信号的奇异值σA,x; (13) 7)比较d1,d2,d3的大小,取其中的最小值所对应的状态为信号x(t)的故障类型. 本文中所用齿轮模拟故障试验台如图9所示.试验平台系统主要由传动轴、驱动电机、齿轮减速箱、直流调速系统、传感器、加载系统、CDSP数据采集仪、CA-1型电荷放大器、以及若干信号传输线和计算机组成. 图9 齿轮模拟故障试验台 试验系统中的齿轮箱为二级传动变速器,齿轮箱传动简图如图10所示,模数m=2,输入轴上的齿轮z1(z=26)与输出轴上的齿轮z4(z4=85)都为正常齿轮,无故障缺陷.为了突出齿轮故障,齿轮箱中各轴承也都完好无损,齿轮的故障模拟主要通过中间轴上的二联齿轮z2(z2=64)以及三联齿轮z3(z3=40)来实现,可用于模拟复合故障,其中2号为正常齿轮,2′号有故障缺陷,3号为正常齿轮,3′和3″有不同的故障缺陷,通过齿轮箱前后两个换档手柄调节齿轮故障. 图10 齿轮箱传动简图 分别采集齿轮在正常,断齿,磨损三种状态下齿轮的振动信号,采样频率为10 000 Hz,采样点数为2 048.获得齿轮振动数据后,分别在每类数据中随机抽取10组数据作为训练的样本数据,余下的数据用于检测该方法的有效性.由于齿轮振动的主要信息集中在高频段,因此这里只选取了后5个IMF分量形成初始向量矩阵A.然后按第2节中的方法计算出测试数据d1,d2,d3的大小,进行模式特征匹配. 表1 不同状态下齿轮振动信号的标准特征向量及其方差 表2 当T=1时对不同类型信号的识别结果 在40组检测信号中只有2组信号识别错误,识别率达到了95.0%.由于齿轮在工作过程中会不可避免地出现信号调制现象,使得其振动信号中出现调幅、调频成分及其边频带,这些成分都是是齿轮故障诊断的重要依据.而EWT分解就是通过分割傅里叶频谱以滤波器组的方式将不同模态信息分离出来,从而提取具有紧支撑傅里叶频谱的调幅-调频成分,即提取出振动信号的主要故障信息.因此由这些高频的调幅-调频IMF分量形成的初始特征向量矩阵A包含了最重要的信息,验证了该方法在理论上的可靠性. 由于是模式识别方法,上述方法同样适用于其它齿轮故障类型的识别.虽然随着齿轮故障类型的增加会增大模式识别的难度,但仍然能保证故障识别的准确率. 为了进行比较,本文采用EMD方法对某一具有磨损故障齿轮的振动信号(表2中的信号②)进行了分析.由于EMD分量的频率是由高到低的,且齿轮振动的频率较高,这里只取了前6个EMD分量,如图11所示.然后对这6个分量进行希尔伯特变换以获得它们的包络谱,其中频谱较为明显的是IMF1的包络谱,如图12所示.根据时频分析理论可知,存在裂纹、破碎或断齿的齿轮将产生该齿轮1X转频振动及该齿轮自振频率的振动,并且在齿轮自振频率两侧有齿轮转速的边带振动,但在图12中对应的故障频谱与齿轮断齿、偏心、不对中等故障的频谱区别不大,因此难以保证故障诊断的正确性. 图11 通过EMD变换得到的对应I(SNR=20 dB) 图12 EMD分量IMF1的包络谱 本文通过对齿轮振动信号进行EWT分解,自适应地获得若干个IMF分量,利用关键的IMF分量形成初始向量矩阵,然后对初始向量矩阵进行奇异值分解,将齿轮振动信号的特征提取出来,获得能够充分描述齿轮振动信号的特征向量,最后通过建立M-距离判别函数来对故障样本数据进行分类.而传统的时、频分析方法对故障特征明显且简单的信号能起到故障诊断的作用,但对复杂微弱的故障信号却很难有效地提取出故障特征,并且由于齿轮振动信号中含有调制信号和谐波成分,使得用这种方法进行故障诊断的难度进一步加大.对实验数据的分析结果表明,将EWT和奇异值分解技术结合能够有效地应用于齿轮的故障诊断中,为齿轮的故障诊断提供了一种新的方法. [1] L 科恩,白居宪,译.时频分析:理论与应用[M].西安:西安交通大学出版社,1998. [2] 李志农,朱 明,褚福磊,等.基于经验小波变换的机械故障诊断方法研究[J].仪器仪表学报,2014,35(11):2423-2432. [3] Gilles J. Empirical Wavelet Transform [J].IEEE Transactions on Signal Processing, 2013, 61(16):3999-4010. [4] Gilles J. Tran G, Osher S. 2D Empirical Transforms,Wavelets,Tidgelets and Curvelets Revesited [J]. SIAM,Journal on Imagine Sciences,2014,7(1):157-168. [5] 陈 浩,郭军海,齐 巍.基于经验小波变换的目标加速度估计算法[J].北京航空航天大学学报,2015,41(1):154-159. [6] 秦 波,刘永亮,王建国,李文卿.基于小波包与奇异值分解的GA-SVM滚动轴承故障诊断方法研究[J].机械设计与制造,2016(6):38-42. [7] 聂振国.基于奇异值分解的信号处理关键技术研究[D].广州:华南理工大学,2016. [8] 程军圣,于德介,杨 宇.基于EMD和奇异值分解技术的滚动轴承故障诊断方法[J].数据采集与处理,2004,19(2):204-209.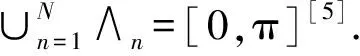
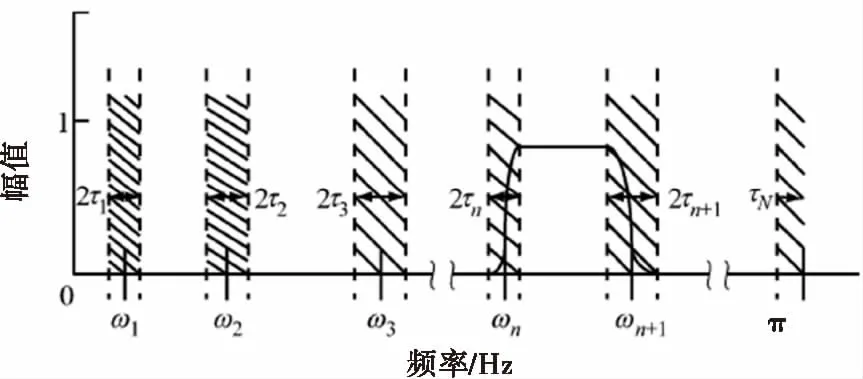
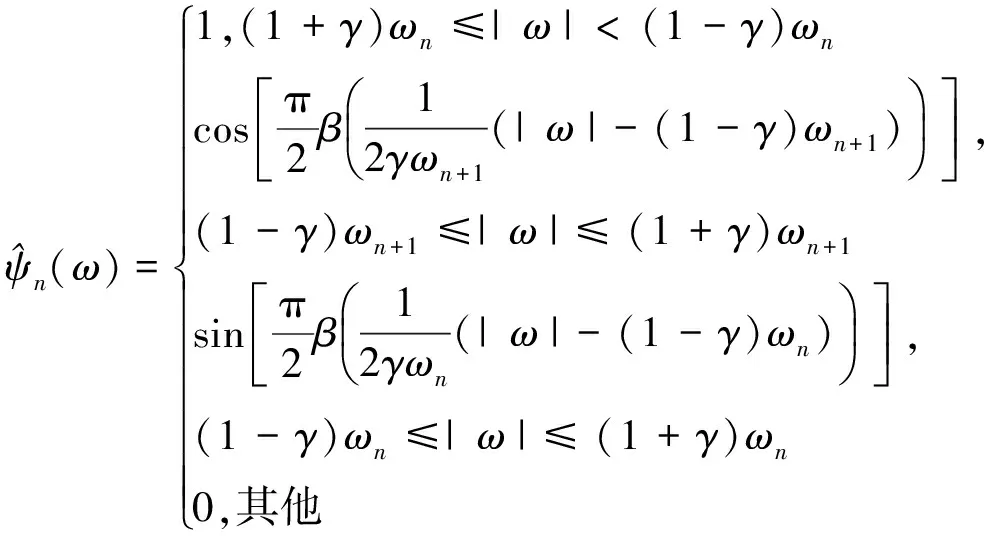
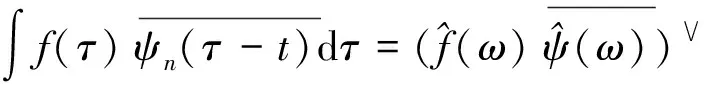
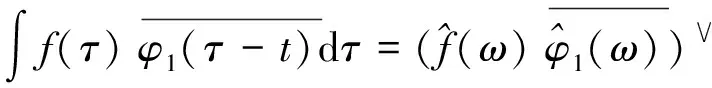
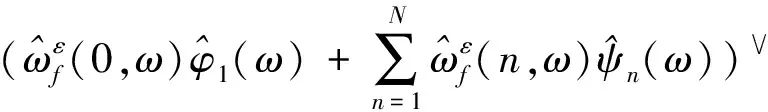
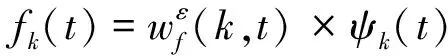

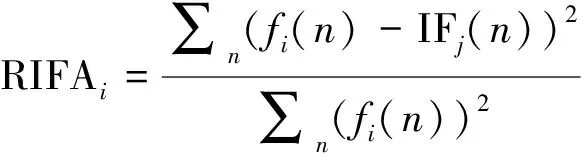
2 基于EWT和SVD技术的齿轮故障诊断方法
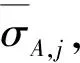
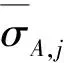
3 实验结果




4 结 语

