软岩非定常分数阶导数流变模型研究

熊德发 王 伟 杨广雨 冯晓伟 赵 腾

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室， 南京 210098； 2. 河海大学 岩土工程科学研究所， 南京 210098)

岩石流变是指岩石矿物组成(骨架)随时间增长而不断调整重组，导致应力、应变状态亦随时间而持续增长变化[1]．岩石流变学的研究在边坡、核废料处置、战略能源储备以及隧道与地下工程等领域具有重要实用价值．岩石流变学研究大致基于经验模型、损伤模型、元件模型，其中，元件模型因数学表达简单、参数物理意义明确等特点被广泛应用，其本构关系是表征应力(应力速率)与应变(应变速率)的关系[2]，本质上是一种整数阶微分型本构关系．

分数阶微积分是整数阶微积分的拓展，是研究任意阶微分与积分的理论[3]．在岩土黏弹性材料的本构研究领域中，Maxwell、Voigt、Kelvin模型不能准确的描述岩土材料复杂的力学行为，然而分数阶微积分能够弥补这方面的不足，为研究岩土材料的流变本构提供了一种新方法．殷德顺等[4]利用分数阶微积分理论，给出了一种软体元件及其本构方程，用来模拟土体，结果表明软体元件模型能够更有效地描述土的流变本构的非线性渐变特性．周宏伟[3]等用Abel黏壶替代Newton黏壶，提出了基于分数阶导数的岩盐流变模型，同时给出了解析解，成功地反映了岩盐流变三阶段特别是加速流变阶段．何志磊等[5]基于分数阶理论，构建了考虑温度因素的流变模型，准确的描述了三峡花岗岩与北山花岗岩在不同温度条件下的流变过程．上述学者基于分数阶理论建立的流变本构模型大多数是基于一维情况，缺少三维流变模型形式．此外，利用Abel黏壶替代经典Newton黏壶来构建蠕变本构模型的本质是考虑了黏性系数的时间相关性[6]．然而，在岩石蠕变过程中黏性系数的非定常特性不仅与时间有关，还与应力水平有关[7-9]．再者，许多流变试验[8，10]发现软岩蠕变的稳态阶段具有明显的非线性特征．

鉴于此，本文提出了一个能够反映应力水平对软岩蠕变稳态阶段非线性特征影响的改进Abel黏壶，将改进的Abel黏壶、经典弹性元件、经典塑性元件与变系数Abel黏壶组合成4元件黏弹塑性模型，并推导出其三维模型形式．通过文献[11]流变试验曲线，利用Levenberg-Marquardt算法分别对一维与三维蠕变本构模型参数进行反演，确定了模型中的参数．

1 软岩非线性蠕变本构模型

1.1 基于分数阶导数的Abel黏壶

分数阶微积分的定义有多种不同的方式，其中，Riemann-Liouville(R-L)型分数阶微积分定义在工科中最常用．R-L型分数阶积分定义为：若f在(0，+∞)上逐段连续，且在[0，+∞]的任何有限子区间上可积t>0，对Re(N)>0，则

(1)

R-L型分数阶导数可看作是分数阶积分的逆运算，定义为：假设f∈C，v>0，m是大于n的最小整数，记v=m-n>0，则称：

(2)

为函数f(t)的n阶R-L型分数阶导数[12]．

1)Abel黏壶描述

Abel黏壶的本构关系为

(3)

当σ(t)=const，即保持应力不变的情况下，对式(3)两侧依次进行Laplace变换与Laplace逆变换，可得

(4)

2)改进的Abel黏壶描述

在岩石蠕变过程中，黏性系数的非定常特性不仅与时间有关，还与应力水平有关．宋飞等[8]通过对角砾岩流变特性的研究，发现角砾岩蠕变的稳态阶段具有明显的非线性特征，黏性系数与应力阈值有关，可用指数函数描述黏性系数的非定常特性．因此，假设黏性系数与应力水平满足以下关系：

(5)

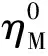
(6)

当σ(t)=const，即保持应力不变，对式(6)两侧依次进行Laplace变换与Laplace逆变换，可得

(7)

图1 不同n值对改进Abel黏壶的影响

图2 不同σ值对Abel黏壶的影响

图3 不同σ值对改进Abel黏壶的影响

对比二图可见，同等应力增量下，Abel黏壶的应变增量相等，而改进的Abel黏壶的应变增量随应力水平的增高而增大，呈现出非线性关系．

3)考虑损伤的Abel黏壶描述

在岩石加速蠕变阶段，因裂纹的产生和拓展，Abel黏壶的黏性系数将发生变化，故在黏性系数中引入损伤因子，因此有

(8)

D为损伤变量，0≤D<1．若不考虑应力影响仅考虑荷载作用时间的影响，岩石在流变过程中的损伤演化可假定成负指数函数形式[4]，即

D=1-e-βt

(9)

式中β为与岩石性质相关的系数．

联立式(3)、(8)及式(9)，考虑损伤的Abel黏壶的本构关系为

(10)

当σ(t)=const时，即保持应力不变，根据Laplace变换，可得

(11)

1.2 一维非线性蠕变本构模型

模型由Hook体、改进的Abel黏壶和考虑损伤的Abel黏壶与塑性体并联组合而成，如图4所示．

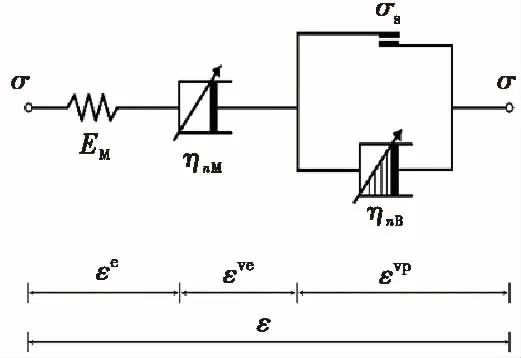
图4 分数阶流变模型

设Hook体的应变为εe，粘弹性体的应变为εve，黏塑性体的应变为εvp，则总应变ε可表述为

ε=εe+εve+εvp

(12)

1)Hook体的应力应变关系为

(13)

2)在改进的Abel黏壶中蠕变本构为

(14)

3)在粘塑性体中，塑性滑块应力σf的大小为

(15)

式中σs为屈服应力．

当σ<σs时

εvp=0

(16)

当σ≥σs时，结合考虑损伤的Abel黏壶的本构关系可得

(17)

式(17)可变为：

(18)

将式(18)依次进行Laplace变换与Laplace逆变换可得到考虑损伤的Abel黏壶蠕变本构为

(19)

即

(20)

综合上述3部分应变，则本文模型的一维本构方程可以表示为

(21)

1.3 三维非线性蠕变本构模型

在三维应力状态下，本文模型的总应变可表示为

(22)

1)根据广义Hook定律，Hook体的三维本构关系为

(23)

式中，sij、eij分别为应力偏张量与应变偏张量，σii、εii分别为应力张量与应变张量的第一不变量，GM为Hook体剪切模量、K为Hook体体积模量．

不考虑体积流变蠕变，故Hook体的三维蠕变本构形式为

(24)

2)在改进的Abel黏壶中三维蠕变本构关系为

(25)

3)黏塑性体中三维本构关系为

(26)

式中

(27)

其中F0为岩石屈服函数初始参考值，通常可取为1，F为岩石屈服函数，Q为塑性势函数，φ(g)为幂函数形式，通常取幂指数m=1[13]．因此联立式(26)与(27)得

(28)

将式(22)、(23)与(26)代入式(20)得

εij(t)=

(29)

在常温中、低温条件下，一般认为球应力张量对蠕变影响很小，应力偏量在蠕变中起主要作用[14]，屈服函数可取为

(30)

在三轴流变试验中，σ2=σ3，故可得

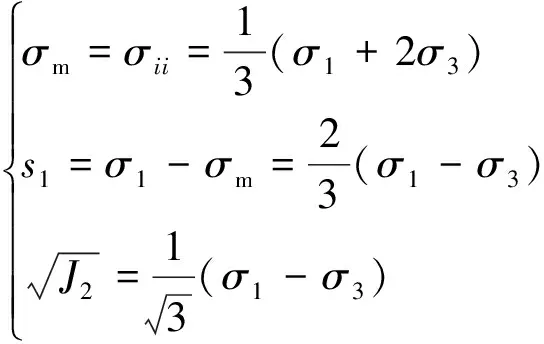
(31)

采用相关联流动法则F=Q，式(29)可表达为

(32a)

(32b)

2 分数阶导数流变模型的参数确定

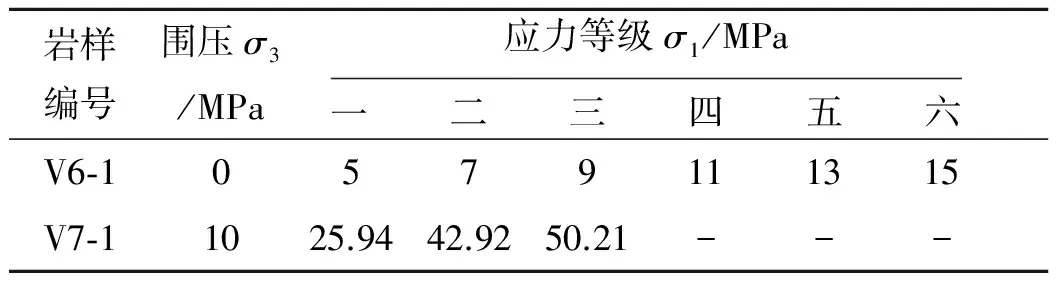
表1 流变试验分级加载应力等级表

图5 一维蠕变模型理论曲线与试验数据对比

表2 软岩一维模型参数计算结果

图6 三维蠕变模型理论曲线与试验数据对比

表3 软岩三维模型参数计算结果

3 结 论

1)基于分数阶导数理论，考虑了软岩稳态阶段的非线性特征，将应力水平对软岩非线性蠕变的影响引入Abel黏壶，提出了一种改进的Abel黏壶，能够更好的反映软岩蠕变稳态阶段的非线性特征．

2)通过对改进的Abel黏壶在同等应力增量下应变增量的对比分析．得到软岩稳态阶段的黏滞系数具有非定常的特性，与时间、应力水平皆有关，并且应力水平愈高，黏滞系数的变化愈大．

3)本文在一维的基础的上推导出了三维蠕变本构方程，建立了三维蠕变本构方程，且模拟效果较好，具有一定的理论指导意义．

[1] 孙 钧．岩石流变力学及其工程应用研究的若干进展[J]．岩石力学与工程学报，2007，26(6)：1081-2106．

[2] 蔡美峰．岩石力学与工程[M]．北京：科学出版社，2002．

[3] 周宏伟，王春萍，段志强，等．基于分数阶导数的盐岩流变本构模型[J]．中国科学：物理学 力学 天文学，2012，42(3)：310-318．

[4] 殷德顺，任俊娟，和成亮，等．一种新的岩土流变模型元件[J]．岩石力学与工程学报，2007，26(9)：1899-1903．

[5] He Z， Zhu Z， Wu N， et al． Study on Time-Dependent Behavior of Granite and the Creep Model Based on Fractional Derivative Approach Considering Temperature[J]． Mathematical Problems in Engineering， 2016：1-10．

[6] 康永刚，张秀娥．岩石蠕变的非定常分数伯格斯模型[J]．岩土力学，2011，32(11)：3237-3241．

[7] 何志磊，等．基于分数阶导数的非定常蠕变本构模型研究[J]．岩土力学，2016，37(3)：737-744．

[8] 宋 飞，赵法锁，卢全中．石膏角砾岩流变特性及流变模型研究[J]．岩石力学与工程学报，2005，24(15)：2659-2664．

[9] 王军保，刘新荣，王铁行．基于改进分数阶黏滞体的岩石非线性蠕变模型[J]．中南大学学报：自然科学版，2015，46(4)：1461-1647．

[10] Yang S Q， Cheng L． Non-stationary and Nonlinear Visco-elastic Shear Creep Model for Shale[J]． International Journal of Rock Mechanics and Mining Sciences， 2011，48(6)：1011-20．

[11] Liu H Z， Xie H Q， He J D, et al. Nonlinear Creep Damage Constitutive Model for Soft Rocks[J]． Mechanics of Time-Dependent Materials， 2016,21(1)：73-96．

[12] Miller K S, Ross B． An Introduction to the Fractional Calculus and Fractional Differential Equations[M]． 1993．

[13] Zienkiewicz O, Cormeau I． Visco-plasticity-plasticity and Creep in Elastic Solids-a Unified Numerical Solution Approach[J]． International Journal for Numerical Methods in Engineering， 1974,8(4)：821-845．

[14] 齐亚静，姜清辉，王志俭，等．改进西原模型的三维蠕变本构方程及其参数辨识[J]．岩石力学与工程学报，2012，31(2)：347-355．

[15] 康永刚．聚合物应力松驰和损耗正切的分数模型研究[D]．重庆：西北师范大学，2007．