基于混合元胞遗传算法的柔性车间调度问题研究

杨宇琪 张 屹 张贵东 陆曈曈

(1. 三峡大学 机械与动力学院， 湖北 宜昌 443002； 2. 三峡大学 经济与管理学院， 湖北 宜昌 443002)

生产调度是制造型企业生产过程中至关重要的环节之一，与生产效率密切相关．运用合理的调度方法可以缩短工期，按时交货且达到机器利用的合理化．作业车间调度问题(job-shop scheduling problem，JSP)是当前生产制造及组合优化等领域的热点问题之一．在JSP中，每道工序均被指定在一台设备上完成加工．若某一工序能够在若干台设备上加工，则作业车间调度问题就扩展为了柔性作业车间调度(flexible job-shop scheduling problem，FJSP)[1-2]．由于FJSP的设备约束减少，导致生产调度柔性更高，更符合制造企业生产现场的实际情况．

目前，海内外诸多研究人员对柔性车间调度问题开展了相关研究．黎冰[3]等针对非确定约束限制的流水作业车间调度问题，构建了含多种参数的混合机会约束规划模型．巴黎[4]等将成品件的完工时间作为优化目标，对该批量装配的FJSP进行建模，运用了粒子群算法求解．唐自玉[5]基于多色集合理论对FJSP进行了研究，提升了机器负荷率、产线负荷均衡率、产线柔性度及有效生产面积利用率，但在解的收敛性方面仍有改进空间．

针对遗传算法在求解FJSP时通常出现的早熟和收敛较慢等问题，本文通过引入多色集合理论，建立了FJSP的多色集合约束模型，并与多目标元胞遗传算法结合，提出了一种基于多色集合的元胞遗传算法，通过在编码、解码及变异过程中，将搜索范围限定为围道布尔矩阵，即有效解范围，以致在保证所得解均是有效解的同时，还能优化最优解的收敛速度．同时还可以利用围道布尔矩阵简化适应度的计算，降低算法复杂度．最后应用改进的元胞遗传算法求解FJSP，并与其它遗传算法求解相同实例的结果进行对比，进而验证该算法的有效性．

1 FJSP优化数学模型的建立

1.1 目标函数的确定

考虑到单目标车间调度优化研究已难以满足制造企业实际的生产要求，于是考虑多个目标，分别是工件的最大完工时间(Cm)，最大负荷机器的负荷(Wm)和机器总负荷(Wt)．其中，最大完工时间影响着每个工件的生产周期，机器负荷与各台机器的使用率成正相关．

1)最大完工时间最小：每个工件开始加工到最后一个工序加工完成之间耗时最长的时间最小，它是评价车间生产高效与否的主要体现．

Cm=min(max(Ck)) 1≤k≤m

2)机器最大负荷最小：负荷最大的机器是瓶颈设备，为提高每台机器的使用率，应使各台机器的负荷尽量小以达到平衡．

Wm=min(max(Wk)) 1≤k≤m

式中，Wm表示序号为m的机器的总时间负荷．

3)总机器负荷最小：不同机器加工同一工序的耗时不同，因此总时间负荷因调度方案的差异性而不同，若最大完工时间相同，则机器的总负荷越小越好．

1.2 约束条件的确定

柔性作业车间调度指的是在生产加工系统中，存在一个需生产加工的作业集，其中包含n个待加工的工件，用集合表示为J=(J1，J2，…，Jn)，包含加工机床集合M=(M1，M2，…，Mm)，该集合中共有m台可供加工的机床，每个待加工的工件均必须经由若干工序才能够完成最终生产．Ojik可被定义为工件i在机床k上加工第j道工序．

工序的加工路径并非唯一，一道工序能在一台或多台机器上完成加工，并且在不同机器上加工耗时均不同．现对常规加工条件进行一定的约束如下：i为工件的序号，i=1，2，…，n；k为机器序号，k=1，2，…，m；j为加工工序号；hij为工件i的加工工序数；tijk为工件i的第j道工序在机器k上加工的耗时；sij为工件i的第j道工序的起始时间；eij为工件i的第j道工序的完工时间；Tij为工件i的第j道工序的加工时间；R为一个无穷大的正整数；ci为每个工件的所有工序完成后的时间；Cmax为最大完工时间；

1)工序约束：在工件加工过程中，必须按照确定的工艺顺序加工，即必须在前一道工序完工之后，下一道工序才可以被加工，故需满足如下条件：

sij+xijk×tijk≤eij

i=1，2，…，n；k=1，2，…，m；1≤j≤hij

(1)

eij≤Cmax

i=1，2，…，n；1≤j≤hij

(2)

2)完工时间约束：工件加工进程中，任意一个工件的完工时间均小于全部工件完成加工的总完工时间，即

cij≤Cmaxi=1，2，…，n；1≤j≤hij

(3)

3)加工时间约束1：工件加工过程中，同一时间内任意一台机床只能加工一道工序，不能加工多道工序，即

eij+eijk≤sef+R(1-yijefk)

i=1，2，…，n；k=1，2，…m；1≤j≤hij

(4)

4)加工时间约束2：工件加工过程中，任意一个工件的任意一道工序的结束时间小于等于该工件下道工序的起始时间，即

eij≤si(j+1)+R(1-yefi(j+1)k)

i=1，2，…，n；k=1，2，…m

(5)

5)机床约束：工件加工过程中，在某一时刻，某道工序只能在某一台允许的机床上加工，不能出现两台或更多机床进行加工的情况，则

；1≤j≤hij

(6)

6)其它约束：上述约束中所提到的各项参数均是大于等于零的正数，即

sij≥0，eij≥0

(7)

2 柔性车间调度的多色集合约束模型的建立

多色集合理论主要用于表达车间调度模型中的约束关系，利用多色集合理论的统一着色及个体着色等概念，建立能够表达柔性车间调度优化模型中的工序与工件之间、工序与机床之间约束关系的围道布尔矩阵．多色集合的颜色集合F(ai)用于描述元素ai的本身属性，称为元素的个人颜色．集合A与全部元素的个体着色F(a)构成的布尔矩阵A×F(a)可表示如下：

F1…Fj…Fm

(8)

矩阵(8)表示了元素的围道组成，对象A所对应的集合F(A)，元素ai所对应的围道集合为F(ai)，ai∈A．如果F(A)∈F(ai)，则cij=1，反之cij=0．基于工件与工序、工序与设备之间存在对应关系，所以用多色集合的围道布尔矩阵可以较为准确地描述作业车间中工件、工序和机床之间的相互关系．

本文以表1中3×5的FJSP为例，说明如何使用多色集合的围道矩阵来描述待加工工序的工艺约束和机床约束之间的关系．

表1 柔性车间调度问题实例

1)工艺约束模型

3个工件的工件-工序围道布尔矩阵见式(9).该矩阵表明：工件1有3道工序，分别为101，102，103．工件2和工件3分别也有3道工序，即为201，202，203；301，302，303．

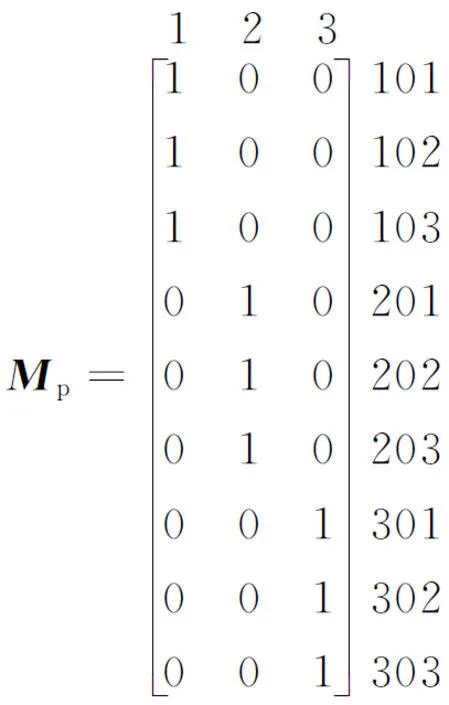
(9)

2)设备约束模型

3个工件的工序-机床围道布尔矩阵见式(10)．

(10)

矩阵(10)的行代表工序编码，列代表机床编码，布尔值为1代表该工序能够使用该机床加工，0则反之．上述矩阵即为加工关系的约束模型，它的功能就是表示同一类工件的工序及对应加工机床的状态．

3 基于多色集合约束模型的元胞遗传算法(PCGA)

Nebro[6]等人在2009年提出的多目标元胞遗传算法(a cellular genetic algorithm for multi-objective optimization，CGA)是一种基于对种群结构进行改进的遗传算法，该算法涵盖了多目标优化理论的核心思想，具有遗传算法的原始理论基础，除此之外，与元胞自动机模型进行了有机结合，是一种包含多种优异特征的集成式优化算法．其算法兼具遗传算法和元胞自动机的优良特性，在求解多目标优化问题时表现出了较好的多样性和收敛性，并在许多实际工程应用中表现效果显著[7]．元胞遗传算法架构如图1所示．

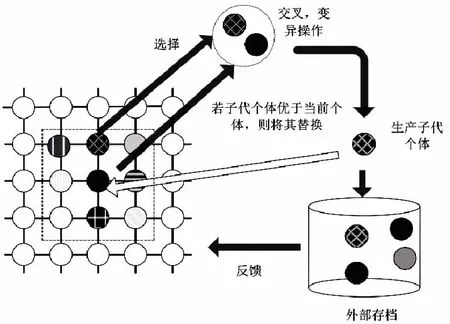
图1 元胞遗传算法架构图

3.1 基于约束模型的编码和解码

目前很多方法均采取基于工序的编码求解经典调度问题，其主要思想是把调度编码成工序序列，单个基因对应单一工序，同样工件的工序采用同样的符号进行表达，继而可由其在指定染色体中出现的次序来诠释．但是该法倾向于解决设备事先确定的调度问题．本文采用双层编码法，即基于工序的编码和基于设备的编码．

1)编码

第1层编码采取自然数编码，因为子代经由遗传操作可以获得父代的优良特征，所以具有优先权原则和Lamarckian特点[8]，同时调度的可行性可以得到有效保证，具有2类解码复杂性，因此可直接采用随机数作为编码基因．如表2所示，101-303共9道工序的第1层编码为1-9的自然数随机排列．

表2 编码方案

第2层编码采用实数编码法，由上述可知第1层编码表达的是所有工序对应的可加工设备编号，因此，已知某道工序，搜索围道矩阵式(10)获得统一颜色为1的对应的多台设备，然后从这些设备编号里任意选取一个作为第2层编码中相应位置的基因，来保证每一个基因的有效性．

2)解码

解码的目的是确定工序的加工顺序．由于第1层编码具有2类解码复杂性[9]，第2层编码却具有0类解码复杂性，即不需要解码，于是，解码是针对第1层编码．

Step1：搜索矩阵(9)，从矩阵中找到每一列首个非0的元素，记下该元素所在行对应的那一道工序．矩阵(9)的行表示同一工件的所有工序的允许先后加工顺序，这样可表示各个工件所有工序之间先后加工的关系约束．

Step2：比较从Step1中挑选出的工序在首层编码中相应的基因值的大小，筛选出值最小的那道工序．

Step3：由Step2可得到基因最小的工件及工序，把矩阵(9)中该工件的相应位置的数值置为0，即摒弃该工序．

不断重复上述3道步骤到全部工序的加工顺序得以确定为止．由于其始终在约束条件下进行，从而保证每一个工件工序是按照先后关系来选择的．

采用以上所述方法，可得到首层编码在进行解码之后的工序先后加工顺序为：201-101-102-301-103-302-303-202-203．由解码后的加工顺序和第2层编码进行对照，可得到加工这些工序的设备依次为：3-2-4-4-1-5-1-2-5．见表3．

表3 解码后的调度安排

3.2 选择操作

在元胞遗传算法中，为了减少选择压力，一般将选择操作限定在邻居中施行．于是，引入一种方法，其能借由个体的适应度自适应选择个体．

以Moore型邻居结构[7]为例，每一个体相邻的8个元胞为其邻居，即左上、左下、右上、右下、上、下、左、右8个方向的个体．首先，通过一定的方式计算邻居的适应度值，找到最差适应度、最优适应度及中心个体适应度，再经由适应度的大小，按照从小到大的次序依次将个体存入集合List．此外还需注意，通过比较相对适应度值更有说服力，因此归一化处理中心个体的适应度值，其后就可得知此个体在邻居中的相对适应度RF，即

然后，在集合List中选取List[round(RF×List.size)]和中心个体施行交叉变异操作，式中round()表示取整操作，List.size表示集合List的大小．

3.3 交叉操作

交叉操作就是通过交换父代之间的染色体，进而生成比父代更优秀的后代．交叉操作的优劣直接决定着子代解的优劣，同时对算法的性能亦会造成相应影响．对于第2层编码，采用直接交叉法，即直接对交叉点间的片段互换．对于第1层编码的交叉操作，则可采用较为传统的线性次序交叉法．根据交叉概率，选出交叉的两个父代染色体P1、P2，得到交叉得到的子代染色体为C1、C2．

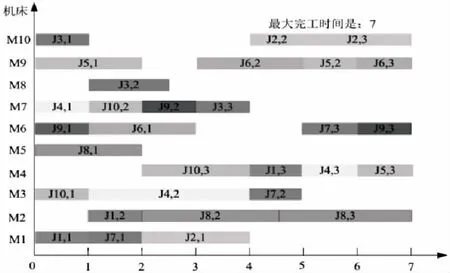
1)随机选择交叉点e1，e2，其中1

2)把P1片段中的第e1→e2位与P2片段中的第e1→e2位进行交换，获得子代C1，C2染色体的一部分基因．(此时C1，C2中只有e2-e1+1个基因)

3)从P1中剔除掉P2中对应的第e1→e2位基因，将P1中剔除之后的剩余基因按顺序填充到C1的空位中．

4)从P2中剔除掉P1中对应的第e1→e2位基因，将P2中剔除之后的剩余基因按顺序填充到C2的空位中．

图2 交叉示意图

3.4 变异操作

对于首层编码，采取互换变异法，也就是随机交换染色体中两个不同基因的相互位置．对于第2层编码，采用多位置替换式变异，首先确定变异位置，然后搜索“工序-设备”矩阵，找出可加工工序的设备．将基因值与上面设备的编号中的任意一个互换，这样就保证了变异之后的基因是有效的．

3.5 PCGA算法流程图

基于多色集合约束模型的元胞遗传算法流程图如图3所示．

图3 PCGA算法流程图

将约束模型引入到遗传算法的具体作用为：

1)去掉无意义的解、无效解，进而保证所得解均为有效解．欲限制非法解的产生，一般有两种方法：①设计新的染色体编码或遗传算子，进而加强解的可行性判断；②利用罚函数来削弱或者消除非法解．本文采用第1种方法，在模型约束下，所有遗传操作之后的染色体个体都代表一个有效的调度方案；且由于约束模型的引入，遗传编码和遗传算子的设计也都被简化处理．

2)缩小解的空间，降低早熟收敛的可能性、改善收敛速度．

4 实例求解与分析

为了评估本文提出算法的性能，选取文献[10]中3种标准测试案例对算法进行测试，分别是8×8，10×10和15×10三种车间调度问题，并与其它算法进行比较，如KACEM[10]、传统GA等．

改进算法使用Java编程，其具体参数为：种群大小100，交叉概率0.5，变异概率0.01，选取Moore型邻居结构．其他算法的参数配置与原文献相同．每一个实例针对3个目标函数分别独立运行10次．测试结果见表4．

表4 测试结果比较

从表4中能够得出，基于多色集合约束模型的元胞遗传算法所求得的结果均小于或等于其他算法求得的最优解，且经过10次运行后的均值亦相对接近最优解，表明本文所提出的PCGA算法在求解多目标柔性车间调度问题时具有一定的优势．

图4是本文算法在8×8问题上求得最大完工时间是14的甘特图，图5是本文算法在10×10问题上求得最大完工时间是7的甘特图，图6是本文算法在15×10问题上求得最大完工时间是11的甘特图．

图4 8×8问题Cm最小值为14的甘特图

图5 10×10问题Cm最小值为7的甘特图

图6 15×10问题Cm最小值为11的甘特图

图7为PCGA与经典GA及CGA之间的迭代对比图，由图7能够看到PCGA的收敛速度相对较快，在50代左右就能够找到最优值．

图7 GA，CGA和PCGA的迭代对比图

综上所述，本文提出的基于多色集合约束模型的元胞遗传算法在求解多目标柔性车间调度上行之有效，与其它算法相比，具有一定的竞争力．

5 结 语

本文针对FJSP展开相应研究，构建了FJSP的多目标优化模型，结合FJSP的特点，通过引入多色集合理论，建立了FJSP的多色集合约束模型，提出了基于多色集合约束模型的元胞遗传算法．与其它算法经过相同的实例测试后，本文所提出的算法所得结果等于或小于其它算法所得结果，同时该算法收敛到最优解的速度更快，且计算过程相对稳定．相比于其它同等条件下的调度优化结果，本文所提出的算法在有效性得到验证的同时具有一定的优势．

[1] 王 凌．车间调度及其遗传算法[M]．北京：清华大学出版社，2003．

[2] 王万良，吴启迪．生产调度智能算法及其应用[M]．北京：科学出版社，2007．

[3] 黎 冰，顾幸生．混合规划处理流水车间调度问题[J]．华东理工大学学报：自然科学版，2006，32(1):98-102．

[4] 巴 黎，李 言，曹 源，等．考虑批量装配的柔性作业车间调度问题研究[J]．中国机械工程，2015，26(23):3200-3207．

[5] 唐自玉．基于多色集合理论的柔性生产线及车间规划方法研究[D]．合肥：合肥工业大学，2009．

[6] Nebro A J， Durillo J J, Luna F, et al． MOCell:Acellular genetic algorithm for multiobjectiveoptimization[J]．International Journal of Intelligent Systems,2009,24(7):726-746．

[7] 鲁宇明．元胞遗传算法研究及应用[D]．南京：南京航空航天大学, 2013．

[8] 郭冬芬，李铁克．基于约束满足的车间调度算法综述[J]．计算机集成制造系统，2007，13(1):117-125．

[9] Alba E， Dorronsoro B．Computing nine new best-so-far solutions for Capacitated VRP with a cellular Genetic Algorithm[J]． Information Processing Letters,2006, 98(6):225-230．

[10] Kacem I, Hammadi S, Borne P． Approach by Localization and Genetic Manipulation Algorithm for Flexible Job-shop Scheduling Problem[C]//IEEE International Conference on Systems, Man, and Cybernetics． IEEE Xplore,2001(4)：2599-2604．