2018年绍兴市中考数学题赏析及教学解析

劳建锋

（浙江省绍兴市建功中学，浙江 绍兴）

对于初中数学教学来讲，加强数学中考题中有关基础性、思想性问题的分析十分重要，其是提升初中生解题能力的基础，也是提升初中生中考成绩的关键。为此，初中数学教师需给予数学中考题中有关基础性、思想性问题的分析高度重视，促使其存在的价值与效用在初中数学教学中充分地发挥。本文主要阐述2018年绍兴市中考数学题赏析及教学解析，具体如下。

一、试题特点

1.基础性。2018年绍兴市中考数学题全面考查了中学生数学素养。试题是《义务教育数学课程标准》内最基础的内容，即学生在学习与运用数学知识优化问题过程中必须掌控的思想方式与基本技能。从核心理念的角度看，试题着重考查了推理、模型以及抽象这三个基本思想。从思想方式的层面看，试题具体考查了分类讨论、方程以及数形结合等思想方法及配方等主要解题方法。从基础知识的层面看，试题具体考查了方程与函数、图形与图形性质之间的关系等重点内容。

比如，第19题：一辆汽车行驶时的耗油量为0.1升/千米，如图是油箱剩余油量（升）关于加满油后已行驶的路程（千米）的函数图象.（1）根据图象，直接写出汽车行驶400千米时，油箱内的剩余油量，并计算加满油时油箱的油量；（2）求关于x，y的函数关系式，并计算该汽车在剩余油量5升时，已行驶的路程。

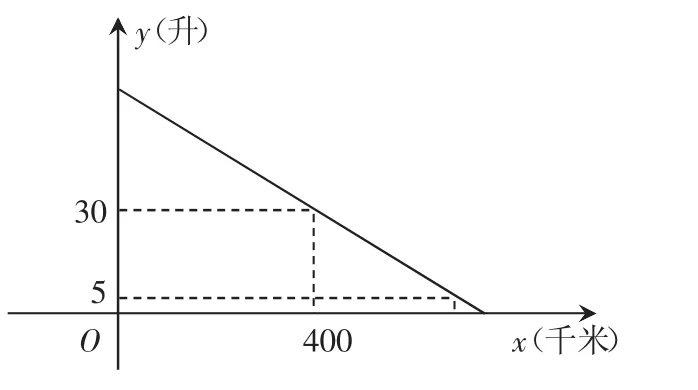
答案：（1）汽车行驶400千米，剩余油量30升，加满油时，油量为70升；（2）已行驶的路程为650千米。

分析：（1）通过观察图象能够得出油箱中的剩余油量，依据油耗量计算出油箱加满油时的油量；（2）采用待定系数法列出一次函数解析式，再代入展开运算。

解题思路：（1）汽车行驶400千米，剩余油量30升，30+400×0.1=70，即加满油时，油量为70升.（2）设y=kx+b（k≠0），把点（0，70），（400,30），坐标分别代入得 b=70，k=-0.1∴y=-0.1x+70，当时y=5，x=650，即已行驶的路程为650千米。

该题主要考查待定系数法，通过运用该方法求一次函数解析式、一次函数图象上点的坐标特征等，重点是掌握待定系数法求函数解析式。

2.思想性。2018年绍兴市中考数学题全面考查了学生使用数学思想方法优化数学问题的能力。中考试题凸显思想性，是数学命题意义的主要体现[1]。

二、教学建议

1.加强学科基础。初中生的数学素养与能力，皆是构建在扎实的知识前提下的，所以，初中数学教师需注重加强学生数学基础知识，其中包含基本技能、思想以及方法等，需明确数学公式、法则以及概念等知识点，并同方程思想、转化思想、概率统计思想以及分类讨论思想等教学思想手段，合理使用相关知识与技能，同个人经验相结合展开数学建模、直观想象、数学抽象、数学运算，以优化现实问题和数学问题。

2.构建有关联系。数学问题的优化一般不是只依靠一个或是几个数学知识，或是一个结合解题方式，而是有关知识同方式的整合应用。所以，数学教师需引导学生构建方法间、知识间的内在联系，需把知识完整化与网络化，要十分注重对网络节点理解和应用，学会使用对比、概括、类比、判断等数学思维方式发现、分析以及优化问题，把已学的知识同经验展开有效迁移，学会站在数学的角度观看世界，运用数学思维探索世界，使用数学方法优化问题[2]。

3.加强推理能力。对于学生来讲推理能力十分重要，数学教师可以通过类比与归纳的方式研究问题，另外还能通过演绎的方式展开推理，让学生通过数学知识学习，可以使用合理推理法发现数学问题，之后采用演绎推理法，对数学结论进行论证，充分掌握数学推理的具体形式，掌握事物间的关系，充分了解知识体系，构成有条理的思维品质，进而加强学生的交流能力。

4.重视过程教学。教学过程中，需要注重过程教学，主要包括两个方面：知识发生发展过程、学生思维活动过程。在教学过程中需要创建问题情境，指引学生发现数据的规律和特点，提出相应的数学问题，对思维活动过程进行展示，使学生在比较的过程中，修正自身的认识，加深学生对数学本质的理解，对数学问题研究的策略、方法、思路、过程进行深入思考和研究，使学生在过程中，对学习进行感悟。

三、结束语

通过上述分析能够发现，2018年绍兴市中考数学题具有较强的基础性、思想性，为了让初中生在中考中得优异的数学成绩，初中数学教师一定要加强对数学中考题中有关基础性、思想性问题的分析力度，让其所具有的实效性在化学教学中发挥最大化，以期为提升初中生数学解题能力与数学素养做铺垫，推动其日后全面发展。