基于邻域旋转体积的关键点描述子及其应用

霍 旺，熊风光，韩 燮，况立群

(中北大学 计算机与控制工程学院，山西 太原 030051)

0 引 言

点云关键点的特征描述作为点云配准与识别等处理中的关键步骤，有着重要的意义与广阔的应用前景。与网格模型相比，散乱的点云数据之间缺少相应的拓扑关系，对关键点的描述更加困难。现有的一些描述算法在运行效率、配准的准确率及抗噪、抗干扰的能力上仍有不足，需要进一步的改进提高。

1 相关工作

针对最近点迭代(iterative closet point，ICP)算法存在的收敛速度慢、计算复杂度高的问题，许多学者提出了先将点云的关键点配准，使两片点云具有良好的初始位置，再利用ICP或其改进算法[1,2]对点云进行精配准的方法。同时提出了许多优秀的关键点描述子算法。但在运行效率、算法的鲁棒性上，仍未取得令人满意的效果，需要人们继续改进和创新。一个有效的关键点描述子必须满足以下条件[3]：①描述子应具有较强的鉴别力；②描述子应具有丰富的描述性和稳健的变换不变性；③描述子应易于计算和匹配；④描述子应对噪声和背景干扰具有较强的稳健性。

目前的描述子根据其描述方式大致可以分为二类：

(1)基于点云空间数据点位置分布的方法。Johnson于1999年提出Spin Image(SI)特征是该类的经典代表。该方法以关键点为圆心，其法向量为z轴构建圆柱参考系，将邻域点的分布密度作为描述的特征。Spin Image对遮挡和干扰具有很强的稳定性，但对点云数据有一定要求，需要点云均匀分布并且需要较大的存储空间。随后Frome提出的3D Shape Context(3DSC)改变了Spin Image投影到二维平面的方式，将邻域划分为三维的球形栅格，统计点云在球形栅格中的特征，其抗噪和抗干扰的性能相比SI均有提高，但进行描述子匹配时需要将场景进行旋转，计算量较大。Rotational Projection Statistics(RoPS)[4-6]是Yulan Guo提出的一种关键点描述子。该方法针对网格表面，在关键点周围建立局部坐标系，将邻域点投影到XOY、YOZ和XOZ这3个2D平面上，并在三平面上建立横平竖直的单元格，根据落到每个单元格的点的数量，来计算每个2D平面上的一系列统计数据(低阶中心矩和熵值)从而进行描述，并且旋转模型增加不同视点时的鲁棒性。RoPS描述子对关键点的描述能力和稳定性都具有了明显的提高，但该方法是基于网格模型进行地描述，而非针对大多数设备获取到的三维点云模型，因此需先对三维点云模型进行三角网格化，而且还要执行多次旋转操作，描述过程较为复杂和耗时。

(2)基于关键点及其邻域点之间几何关系的方法。这类方法比较有代表性的是Rusu R.B提出的Point Feature Histogram(PFH)特征和改进算法Fast Point Feature Histogram(FPFH)等相关算法[7,8]。该方法是将关键点邻域内每一对点建立达布坐标系(Darboux frame)，计算法向量与坐标系的夹角，形成能描述关键点邻域关系的直方图。FPFH算法的优点是算法简单、计算速度快，缺点是抗噪性差。Signature of Histogram of Orientations(SHOT)[9]特征描述了邻域内不同空间位置点的法向量与局部坐标系的夹角关系。其具有很好的抗噪性，但描述子的维数达到了352维之巨，因此计算时间较长。

本文提出一种建立在局部坐标系的基础上，首先对关键点的邻域点进行区间划分，然后对各个区间内邻域点与投影到特定平面上的投影点所形成的各个梯形进行360°旋转，最后通过计算经旋转后得到的空间模型的体积的数值对该区间进行描述，形成一个对关键点的多区间体积值进行表述的描述子。本文提出的描述子描述的也是关键点及其邻域点之间几何关系。描述子利用了局部坐标系，因此具有良好的旋转平移不变性；同时，关键点及其邻域点投影形成的几何模型的体积计算方法简单易行、效率高，并且最终所形成的描述子的低维度性有利用后期描述子的匹配。

2 描述子建立过程

(1)获取关键点p的邻域点。以关键点p为球心，R为半径建立一个p的邻域球，记为S，包含在该球内的所有点即为p的邻域点，记为Nbhd(p)。本文采用KD-Tree进行空间邻域点搜索，加速关键点的邻域点的查找速度。

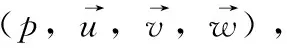
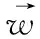
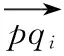
(1)

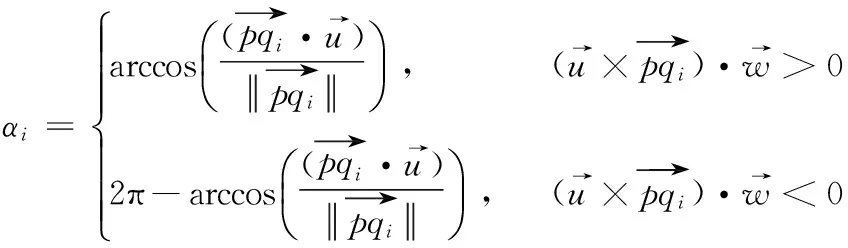
(2)

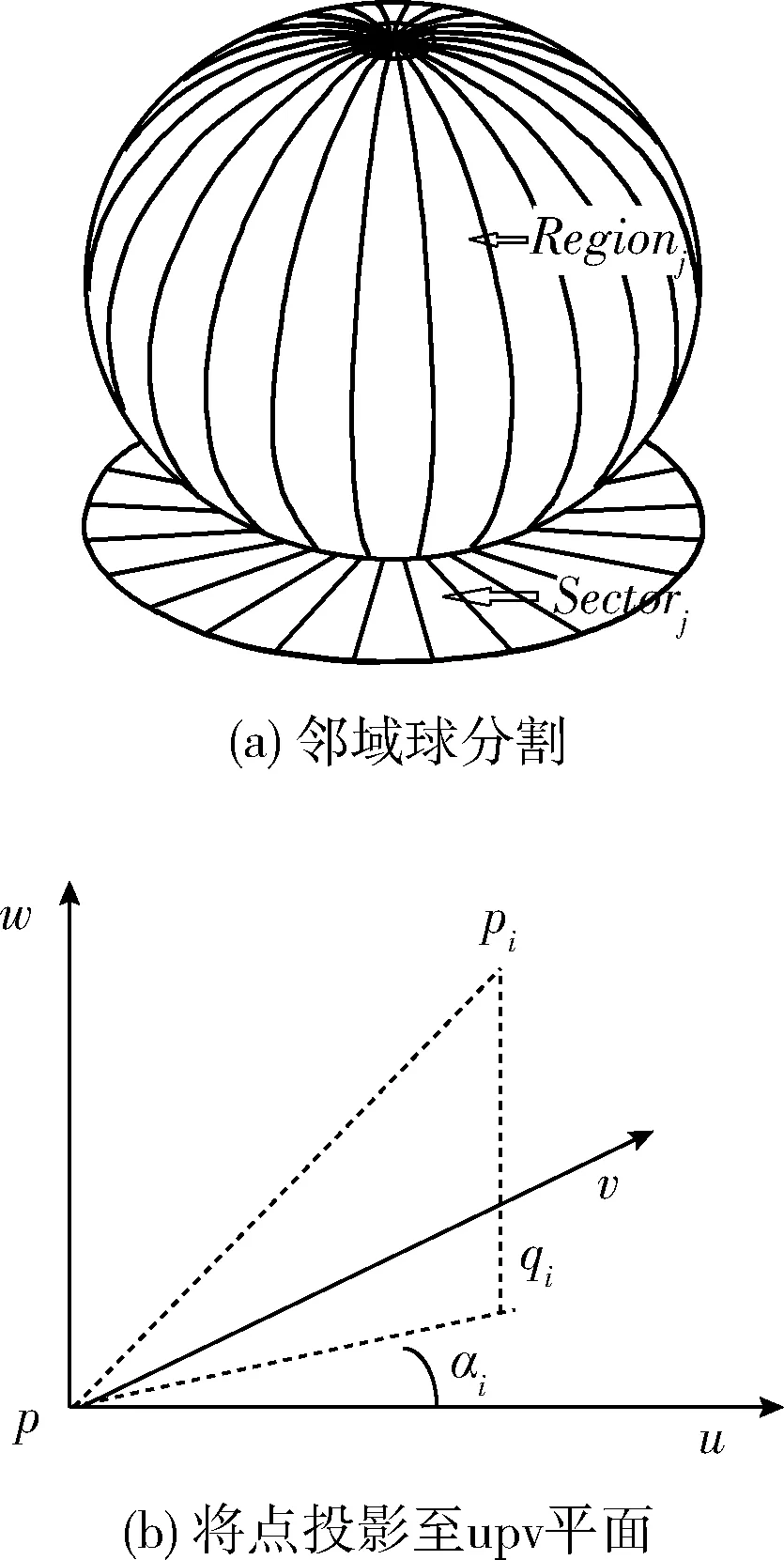
图1 空间的几何区间

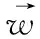
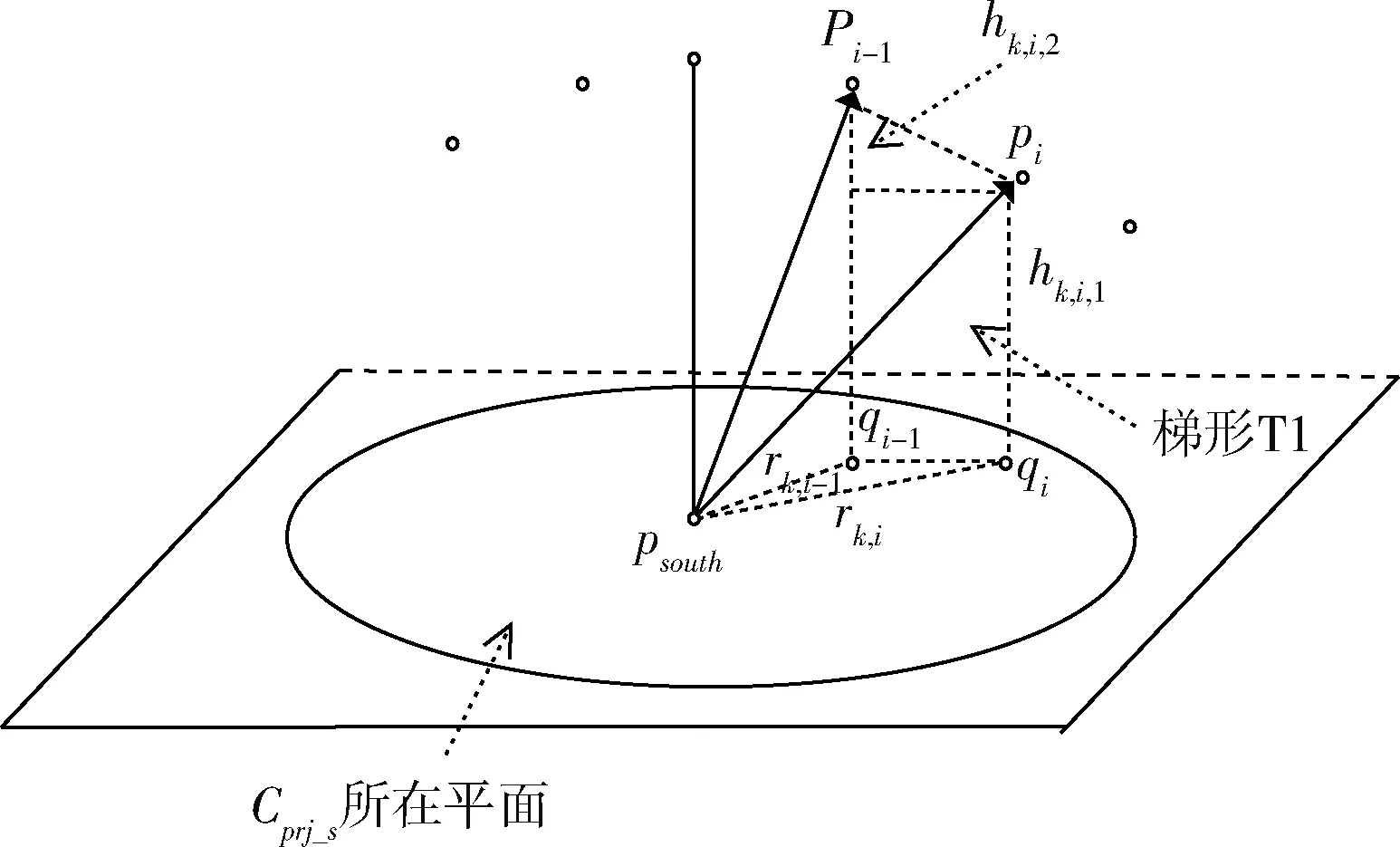
图2 任一空间区域侧视图

在计算Regionk中两相邻邻域点及其投影点所形成的梯形旋转后的模型的体积Vk,i时，可将该模型拆分为一个空心圆柱体Modelk,i,1和一个中间为空心圆柱的圆台Modelk,i,2。Modelk,i,1的体积Vk,i,1可用式(4)进行计算，其中，hk,i,1代表的Modelk,i,1的高，rk,i-1和rk,i分别代表Modelk,i,1的内、外半径，均可通过式(6)进行计算。Modelk,i,2的体积Vk,i,2可由圆台的体积Vk,i,3与圆柱的体积Vk,i,4相减而得，见式(7)。式(8)用于计算体积Vk,i,3,其中hk,i,2代表圆台的高，rk,i-1和rk,i分别代表圆台的内、外半径，也通过式(6)进行计算。式(9)用于计算体积Vk,i,4，其中hk,i,2代表空心圆柱的高，通过式(10)进行计算，rk,i-1代表圆柱的半径。另外，rk,0=0，hk,0,1=R

(3)

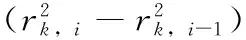
(4)

(5)

(6)

Vk,i,2=Vk,i,3-Vk,i,4

(7)

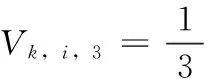
(8)

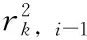
(9)

hk,i,2=hk,i-1,1-hk,i,1

(10)

(6)依据步骤(5)，计算关键点p的其它m-1个维度的数值，最终组成一个m维的描述子。

3 实验结果及分析

实验采用与PFH、FPFH、SHOT描述子在运行时间、旋转平移鲁棒性、抗噪性和降采样方面进行对比分析。三维模型使用斯坦福大学的标准三维模型库中的Bunny、Armadillo和Happy Buddha，以增加不同模型情况下的对比性。本文所提出的描述子代码采用VS2013平台+PCL库实现，且PFH、FPFH、SHOT在PCL中有开源代码，可以很方便地进行对比分析；另外，本实验中设定m为24，点云的法向量是基于最近的10个邻近点获取的，邻域半径R为18倍的点云分辨率。

3.1 运行时间分析

表1是实验用的模型信息，记录了各模型中点的个数和获取到的关键点的个数，本文利用PCL中提供的HarrisKeypoint3D类将提取到Harris 3D角点作为关键点。表2记录了4种描述子的维数和在不同模型下生成关键点的描述子所需运行时间的对比。从表2可以看出本文提出的描述子无论是维数、计算时间都较小，意味着所需的存储空间较小、计算效率更高、实时性将更好，其原因是本文所提出的描述子只需要计算关键点处的局部坐标系和各邻域内的体积和，不需要计算其它额外的参数(如：法向量、网格等)，所以运行时间大大缩短。最终的运行时间只与关键点的多少有关，而和模型的点数等其它参数无关。

表1 实验模型信息

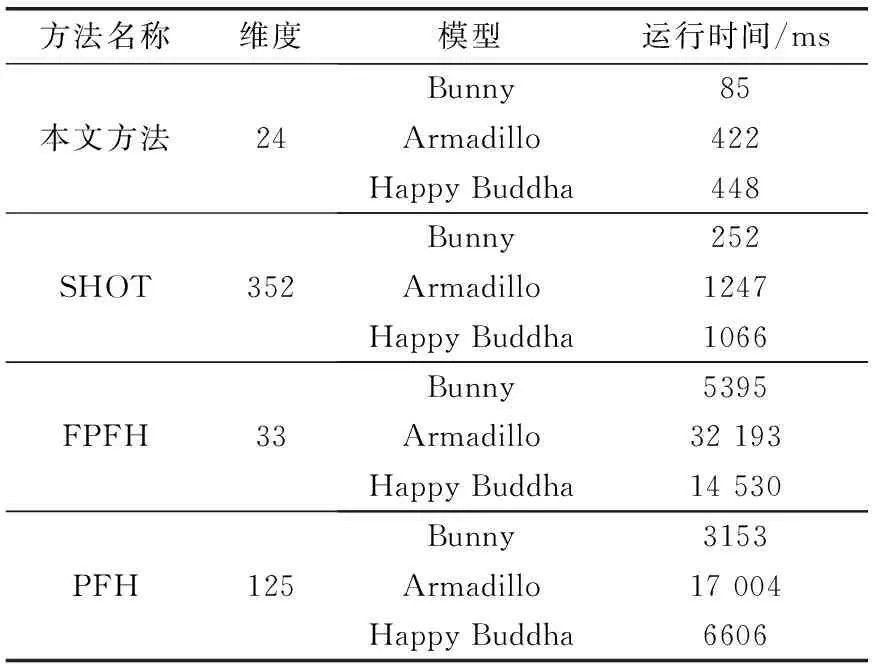
表2 各个方法不同模型的运行时间

注意本文实验出现了PFH比FPFH快的情况。其原因是实验采用的是对关键点而不是整个点云进行的描述。根据FPFH的原理相当于扩大了邻域搜索半径，但由于计算的关键点数目较少，FPFH提高的效率不能弥补扩大半径的带来的劣势。故而会出现下表中PFH比FPFH快的情况，但这并不影响对结果的分析。

3.2 旋转平移的鲁棒性分析

在三维点云获取过程中经常由于物体形状、设备等限制，不能获取连续的、视点不变的点云，经常带有一定的旋转角度。因此，描述子旋转平移的鲁棒性是评价一个描述子的重要标准。

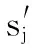
匹配准确率=正确匹配的描述子对的数目/匹配的描述子对的数目

(11)

图3为3个模型在不同描述子下的旋转平移不变的鲁棒性分析结果。从图3中可以看出本文提出的描述子与其它描述子相比，对旋转平移具有更好的稳定性。在旋转较大角度时仍有较高的准确率，同时针对不同模型表面都能有较好的表现。分析原因主要有：一是本文采用基于关键点建立局部坐标系的方式进行描述，本身局部坐标系具有良好的旋转平移鲁棒性；二是采用模型几何体积分布的方式对局部点云进行描述，只要是模型的几何结构不发生变化，经旋转平移后仍能保持局部点云的体积分布不变。

3.3 抗噪性分析

在三维点云数据的获取过程中，由于人为、环境的干扰或者扫描设备本身的设计缺陷、精度限制等问题，使得获取到的点云数据多带有一定的噪声。因此，需要对点云加入高斯噪声，并进行旋转平移鲁棒性检验来考察描述子的抗噪性能。

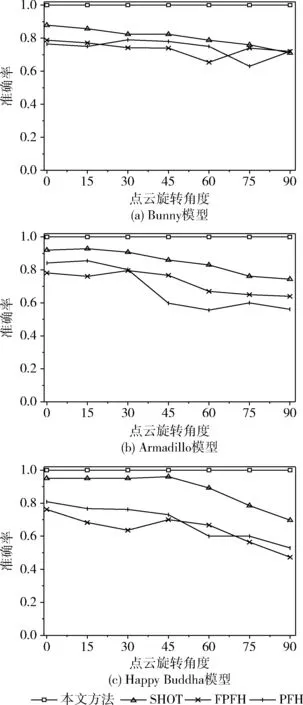
图3 旋转平移的鲁棒性分析

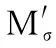
图4 抗噪性分析

从图4可以看出相较于其它描述子而言，本文所提出的描述子具有很好抗噪性，究其缘由，还是因为本文所提出的描述子仅仅是描述关键点的空间几何体积，只要是噪声没有对模型的几何结构产生重大的影响，描述子的稳定性就不会发生太多变化。

3.4 不同采样率分析

生产、生活中，经常会有采样设备的硬件、配置不同等情况，获取的点云的采样率也不尽相同。因此，基于不同采样率，实验测试描述子的性能显得尤为重要。

本次实验的过程为：给定一个模型M、一个真实的旋转平移矩阵Rt，M进行采样率为δ的降采样后的模型记为Mδ，Mδ在Rt的映射下的模型为Mδ′；然后按照3.2中的实验依据模型M、Mδ′和旋转平移矩阵Rt进行旋转平移鲁棒性分析。实验结果如图5所示。

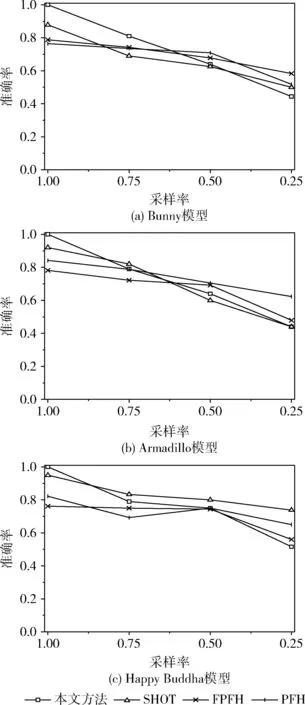
图5 多采样率分析

从图5可以清晰看出本文所提出的描述子，在采样率为3/4左右时，具有良好的效果，在采样率为1/2左右时，性能接近于其它描述子，而当采样率为1/4左右时，性能差于其它描述子，其原因是本文的描述子在分辨率下降较多的情况下，内部几何结构发生较大改变，体积计算产生较大的误差，影响了描述子的性能。

4 本文描述子的应用

将本文所提出描述子应用于点云配准中，实现多视角下点云的对齐操作。实验数据为斯坦福大学提供的不同视角下的兔子的点云模型，包括从0°、45°、90°、180°、270°和315°的6个不同视角下扫描的点云。其中两片点云的配准过程为：

(1)载入视角相邻的两片点云(如：0°、45°)记为source、target，并分别提取Harris 3D角点作为关键点集合keys_src和keys_tgt，利用本文提出的方法对关键点进行描述，获得两组描述子集合feature_src和feature_tgt，其中关键点集合中的关键点与描述子集合中的描述子是一一对应的；

(2)随机选取feature_src中的3个描述子fs0、fs1和fs2，置入集合fs中，利用KD-Tree在feature_tgt中为fs0搜索5个最近的描述子，并随机选取一个描述子ft0作为fs0对应描述子，依次计算出fs1的对应描述子ft1，fs2对应描述子ft2，将ft0、ft1和ft2置入集合ft中；

(3)找到fs0、fs1和fs2对应的关键点ks0、ks1和ks2，依次连接该3点形成3条边并计算它们的欧式距离，分为记为d_ks01、d_ks12和d_ks20，同理计算ft0、ft1和ft2对应关键点所形成3条边的欧式距离，分别记为d_kt01、d_kt12和d_kt20，依次计算对应边距离的相似比，即min(d_ks01/d_kt01，d_kt01/d_ks01)、min(d_ks12/d_kt12，d_kt12/d_ks12)和min(d_ks20/d_kt20，d_kt20/d_ks20)，如果相似比均大于一定阈值(本文为0.8)时则继续步骤(4)，否则退回到步骤(2)；

(4)利用步骤(3)找到的3对关键点、和，计算出旋转矩阵平移Rt；

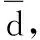
(6)循环n次(本文为50000)执行步骤(2)～步骤(5)，选取最小fitness时的旋转平移矩阵作为最终的旋转平移矩阵。根据这个旋转平移矩阵可以将source变换到target同一坐标系下，完成根据关键点对点云的配准工作。

对每两个相邻的点云片依次执行上面的操作，最终可以将6片点云都变换到同一坐标系下，得到完整的模型。本文的配准结果如图6所示。

图6 基于本文所提出的描述子的配准

从图6可以看出，配准结果还是相对较好的。基本上吻合了兔子本身的位置，虽然耳朵等处有些误差，但仍在可接受的范围内。达到了粗配准的要求，可以为后续精确配准提供良好的初始条件。

5 结束语

本文提出了一个基于关键点邻域旋转体积特征的描述方法。实验结果表明，针对不同点云模型都具有非常好的旋转平移鲁棒性，同时具有描述过程中所需存储空间较小，运行速度快的优势。在模型具有噪声、采样率差别较小的情况下仍有良好的表现。比PFH、FPFH和SHOT等描述子运行的更快，更稳定，且应用在多片点云的粗配准上也达到了较好的效果，为下一步的精配准做了良好的铺垫。但是在模型采样率差别较大的情况下，效果并不理想，接下来的研究可以针对此问题进行改进。

[1]Chen J,Belaton B.An improved iterative closest point algorithm for rigid point registration[J].Communications in Computer & Information Science,2014,481:255-263.

[2]Tagliasacchi A,Schröder M,Tkach A,et al.Robust articulated-ICP for real-time hand tracking[J].Computer Graphics Forum,2015,34(5):101-114.

[3]GUO Yulan,LU Min,TAN Zhiguo,et al.Survey of local feature extraction on range images[J].Pattern Recognition and Artificial Intelligence,2012,25(5):783-791(in Chinese).[郭裕兰,鲁敏,谭志国,等.距离图像局部特征提取方法综述[J].模式识别与人工智能,2012,25(5):783-791.]

[4]Guo Y,Sohel F,Bennamoun M,et al.Rotational projection statistics for 3d local surface description and object recognition[J].International Journal of Computer Vision,2013,105(1):63-86.

[5]Guo Y,Bennamoun M,Sohel FA,et al.3D free form object recognition using rotational projection statistics[C]//Applications of Computer Vision.FL:IEEE,2013:1-8.

[6]Guo Y,Sohel F A,Bennamoun M,et al.RoPS:A local feature descriptor for 3D rigid objects based on rotational projection statistics[C]//International Conference on Communications,Signal Processing, and Their Applications.Sharjah:IEEE,2013:1-6.

[7]Rusu RB,Bradski G,Thibaux R,et al.Fast 3D recognition and pose using the Viewpoint Feature Histogram[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Taipei:IEEE,2014:2155-2162.

[8]Li P,Wang J,Zhao Y,et al.Improved algorithm for point cloud registration based on fast point feature histograms[J].Journal of Applied Remote Sensing,2016,10(4):045024.

[9]Salti S,Tombari F,Di stefano L.Shot:Unique signatures of histograms for surface and texture description[J].Computer Vision and Image Understanding,2014,125(8):251-264.

[10]Zaharescu A,Boyer E,Horaud R.Keypoints and local descriptors of scalar functions on 2d manifolds[J].International Journal of Computer Vision,2012,100(1):78-98.

[11]Petrelli A,Stefano LD.On the repeatability of the local refe-rence frame for partial shape matching[C]//IEEE International Conference on Computer Vision.Barcelona:ICCV,2011:2244-2251.