基于能量法的露天开采下采空区顶板安全厚度研究
李玉飞 叶义成,2 胡南燕 胡盛栋 罗斌玉 元宙昊
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室,湖北 武汉 430081)
我国一些露天开采的老矿区,受开采规划或矿床勘探的影响,在露天开采境界内往往遗留浅埋采空区。露天矿山逐层向下剥离时,采空区覆岩厚度逐渐减小。在地面机械施工荷载作用下,露天矿山下伏采空区顶板安全厚度不足时,将诱发采空区顶板突发性冒落,对采空区上方作业人员和采掘设备构成安全隐患。因此,合理确定采空区顶板安全厚度是保障露天矿安全生产的重要工作。
目前,针对采空区顶板安全厚度的研究取得了较多成果。王树仁等[1]基于Reissner厚板理论,考虑了施工机械的动荷载作用,建立了采空区顶板安全厚度表达式;燕恩科等[2]采用厚度跨比法、普氏压力拱法、鲁佩涅伊特理论和三维数值模拟法联合确定了采空区顶板最小安全厚度;周晓超等[3]基于改进梁模型,推导了地下空区不同跨度下顶板安全厚度;林杭等[4]借鉴边坡稳定性分析的强度折减法,提出了采空区安全顶板预测的厚度折减法;张敏思等[5]采用RFPA数值模拟,获得了采空区顶板发生初始损伤和失稳垮塌时的临界跨度和顶板安全厚度;邓鹏宏等[6]建立了车辆荷载作用下采空区顶板的力学模型,获得了空区顶板安全厚度计算式;何忠明等[7]基于厚度折减理论,采用FLAC3D建立了双层空区数值模型,计算了不同空区跨度下的顶板安全厚度;柳小波等[8]采用第一强度理论建立了均布载荷和集中载荷共同作用下的空区顶板安全性控制方程,得到了安全临界顶板厚度;甄云军等[9]采用强度折减技术和二分法原理,通过FLAC计算出各种跨度空区在不同岩层中的最小安全顶板厚度。
大多数学者基于顶板的力学行为对采空区顶板安全厚度进行了研究,为矿山安全开采提供了理论支撑。然而,采空区顶板失稳破坏过程的应力、应变较为复杂,从能量角度可以避免研究采空区顶板结构失稳破坏的中间复杂受力过程[10]。同时,露天开采下采空区顶板破坏失稳是一个非线性、不连续性的突变过程,而突变理论是研究不连续性现象的新兴学科[11-12]。因此,可以考虑从能量守恒和突变失稳的角度研究露天开采下采空区顶板安全厚度。近年来,突变理论在岩体系统动力失稳中应用广泛。任智敏、张钦礼、赵延林等[13-15]基于突变理论研究了大跨度巷道顶板、矿山采场以及采空区重叠顶板失稳问题;马莎、郑东健等[16-17]建立了地下洞室和高拱坝失稳的尖点突变模型;杨治林、邵爱军等[18-19]采用突变理论分析了回采巷道底板岩层失稳破断和矿坑底板突水机理。以上应用证明了突变理论可以解释矿岩系统结构失稳的非线性动力学特征。
本研究基于材料力学、弹性力学等基础力学理论,分析露天采场下采空区顶板受力状态,建立固支梁力学结构模型;根据能量守恒原理,研究由顶板弯曲应变能、水平荷载做功和垂直均布荷载做功组成的采空区顶板结构总能量方程,从而表达采空区顶板势能函数;采用突变理论,建立采空区顶板系统的尖点突变模型,获得采空区顶板失稳判别式,进而推导采空区顶板安全厚度计算模型。
1 采空区顶板结构力学模型及总能量
1.1 采空区顶板结构力学模型
为了便于分析,将地表机械施工设备拟为静力荷载,按等效均布的方式作用在采空区顶板上方[20]。采空区顶板承受机械施工设备的动荷载作用,按静力荷载处理时需要乘以动荷载系数。露天开采下采空区顶板受力发生弯曲变形,顶板所受上覆岩层荷载qr及机械施工设备荷载qs之和可视为垂直均布荷载q,同时考虑采空区顶板受侧向水平荷载p。在垂直均布荷载q及水平荷载p共同作用下,容易引发采空区顶板突发失稳。采空区顶板两端嵌入围岩中,视为顶板两端无角位移和线位移,将其简化为固支约束。顶板视为仅在轴向有变形,在其他方向不发生变形的定向支座,则采空区顶板可简化为如图1所示的固支梁力学结构模型。假设顶板岩梁在受力变形过程中始终保持在弹性范围内,且服从平截面假设。采空区顶板长度为a,宽度b(研究取单位宽度1 m),顶板厚度为h。
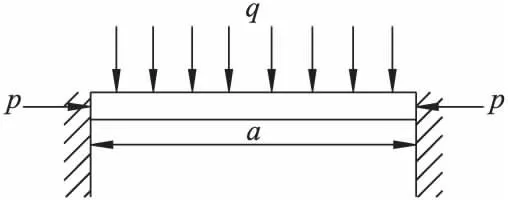
图1 固支梁力学结构模型Fig.1 Mechanical structure model of clamped-clamped beam
1.2 采空区顶板结构总能量
根据能量原理[21-22],并结合采空区顶板力学结构模型分析得到顶板结构总能量
W=U+Wp+Wq,
(1)
式中,U为顶板弯曲应变能,J;Wp为水平荷载做功,J;Wq为垂直均布荷载做功,J。
根据边界条件,顶板岩梁的挠曲线方程:
(2)
式中,δ为常量;s为从顶板岩梁端点到轴线上任意点的弧长,m。
顶板弯曲应变能
(3)
式中,I为顶板岩梁断面的惯性矩,m4;M(x)、K(x)为顶板岩梁弯曲后,以岩梁端点为原点的挠曲线上的弧坐标在s处横截面上的弯矩和挠曲线曲率;μ为顶板岩体的泊松比;E为顶板岩体的弹性模量,MPa。
挠曲线上任意点s处变形后的单元弧如图2所示,由于sinθ=(df)/(ds)=f′,θ=arcsinf′,顶板岩梁变形曲线在s处的曲率:
(4)
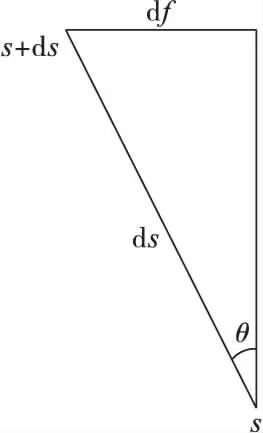
图2 s处形变后的单元弧Fig.2 Element arc after deformation at s
将式(4)代入式(3)后作Taylor展开,再将式(2)代入积分,省略余项和常数项得:
(5)
水平荷载p做功
Wp=-pε,
(6)
式中,ε为顶板岩梁在水平荷载作用下的位移量,m。
顶板岩梁两端的位移量
(7)
将式(7)作Taylor展开,省略余项和常数项得:
(8)
将式(8)代入式(6),再将式(2)代入积分得:
(9)
其中,水平荷载p的计算公式为
(10)
式中,χ为侧压力系数;μ0为上覆岩层的泊松比。
垂直均布荷载q做功
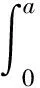
(11)
将式(2)代入式(11)积分得:
(12)
由于将采空区顶板视为单位宽度的固支梁,此时顶板岩梁所受垂直均布荷载q为线荷载。则垂直均布荷载q的计算公式为
q=qr+qs=γHb+νF,
(13)
式中,γ为上覆岩层容重,kN/m3;H为上覆岩层高度,m;ν为动荷载系数;F为顶板岩梁所受机械施工荷载,kN/m。
将式(5)、式(9)、式(12)代入式(1)中,得到顶板结构的总能量方程,即采空区顶板系统势函数解析式:
(14)
2 采空区顶板系统尖点突变模型
突变理论作为研究岩体系统动力失稳的一个数学理论,它注重研究系统中某些变量为何从连续逐渐变化导致系统状态的突然变化[23-24]。其中,尖点突变模型因其临界曲面容易构造,几何直观性强,目前应用最为广泛,本研究选用此模型。
尖点突变模型势函数的标准形式可表示为
W(x)=x4+mx2+nx,
(15)
式中,x为系统的状态变量,m、n为控制变量;x、m、n构成势函数的三维空间。
根据式(14)和式(15)可知,采空区顶板系统势函数W的空间曲面可由尖点突变模型的平衡曲面和分叉集表示,如图3和图4所示。平衡曲面的折痕在m—n平面上的投影为系统的分叉集,分叉集将m-n平面分成2个区域,在较小区域内存在2个稳定平衡点和1个不稳定平衡点,在较大区域内只有1个稳定平衡点。
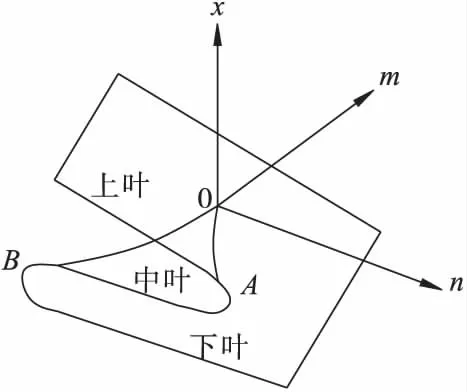
图3 尖点突变模型的平衡曲面Fig.3 Balance surface of the cusp catastrophe model
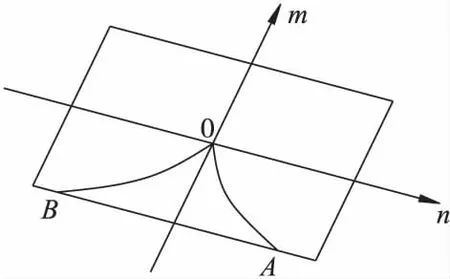
图4 尖点突变模型的分叉集Fig.4 Bifurcation set of the cusp catastrophe model
令
对式(14)作变量代换,将其转化为尖点突变模型的标准形式:
(16)
根据式(15)和式(16)得到尖点突变模型的控制变量参数:
(17)
3 采空区顶板安全厚度计算模型
3.1 计算模型
对式(15)进行求导,得到采空区顶板系统平衡方程为
W′(x)=4x3+2mx+n.
(18)
如图3所示,W′(x)=0方程为尖点突变模型的平衡曲面。平衡曲面分为上叶、中叶和下叶,顶板状态随着状态变量x的变化而变化。
将W′(x)=0方程与W′′(x)=0方程联立消去x,得到分叉集方程:
Δ=8m3+27n2.
(19)
从图4可以看出,只有满足m≤0时,系统才能跨越分叉集发生突变失稳。因此,系统发生突变失稳的必要条件为m≤0。
根据式(17),并将I=h3/12代入得:
(20)
由式(20)知,当采空区顶板所受侧向水平荷载p越大,顶板岩体的弹性模量E越小,顶板厚度h越小,采空区顶板长度a越大,采空区顶板越容易发生突变失稳。由于采空区顶板所受侧向水平荷载p、顶板岩体的弹性模量E、顶板厚度h等几何力学参数是采空区顶板内部特性。因此采空区顶板突变失稳的必要条件与采空区顶板内部特性有关,与外部条件无关。
如图4所示,分叉集方程是系统稳定性的平衡方程。当Δ>0时,W′(x)=0方程只有1个实数根,对应有1个平衡位置,此时系统处于稳定状态;当Δ<0时,W′(x)=0方程有3个实数根,对应有3个平衡位置,此时控制变量(m,n)已越过分叉集,系统处于失稳状态;当Δ=0时,W′(x)=0方程有3个实数根,对应存在2个平衡位置和1个非平衡位置,当控制变量(m,n)越过分叉集上B点时,系统必然发生突跃,系统处于失稳状态。因此,当Δ=0时,采空区顶板系统处于临界平衡稳定状态,构成系统发生突变失稳的充分条件。
将式(17)代入式(19)中,再将I=h3/12代入,得到采空区顶板失稳的临界判别式:
(21)
由以上分析知,当Δ>0及m>0时,构成了采空区顶板系统保持稳定的充要条件。则采空区顶板安全厚度表达式为
(22)
为简化计算模型,将采空区上覆岩层和顶板岩体视为同一岩层,则上覆岩层泊松比μ0和顶板岩体泊松比μ相等,即μ0=μ。
将式(10)代入式(22)中,进一步得到采空区顶板安全厚度
(23)
采空区顶板临界厚度函数关系式为
(24)
由式(22)和(24)知,露天开采下采空区顶板安全厚度与采空区长度a、垂直均布荷载q、水平荷载p、顶板岩体泊松比μ、顶板岩体弹性模量E等有关。因此,影响露天开采下采空区顶板安全厚度因素较多,并非是单一的。通过合理布置采场结构参数、控制采空区上方机械施工荷载大小等措施,改变影响采空区顶板厚度的因素大小,保证各相关因素在合理安全范围内,确保采空区顶板安全厚度不小于其临界厚度,使它们不满足顶板系统发生突变失稳的充要条件,从而控制采空区顶板失稳的发生。
3.2 工程验证
某露天矿境界内遗留有浅埋采空区,这些采空区是由于采用房柱式回采方法形成的,其工程模型如图5所示,采空区顶板受力可简化为图1所示的力学结构模型。
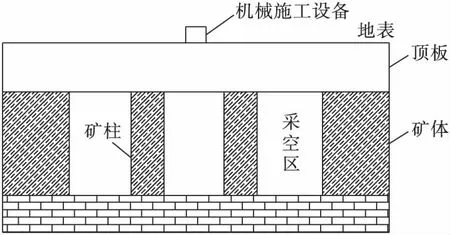
图5 工程模型Fig.5 Engineering model
选取该区域某一采空区为研究对象,该采空区岩性主要为页岩、砂岩、粉砂岩。采空区长度a=20 m,宽度8 m,埋深为H=80 m。采空区顶板岩体的弹性模量E=2 200 MPa,容重γ=26.5 kN/m3,泊松比μ=0.24。地表机械施工设备对采空区顶板岩梁产生的荷载为F=320 kN/m,通过查阅常用机械设备动荷载系数表,该机械设备的动荷载系数取ν=2。
根据式(13)计算出垂直均布荷载q=2 760 kN/m,将各值代入式(24)中,解得采空区顶板临界厚度h=5.67 m。考虑到工程安全,理论计算的临界顶板厚度值应乘以工程安全系数,该工程安全系数取2,则最终临界顶板厚度为h=11.34 m。当h>11.34 m时,采空区顶板保持稳定;当h<11.34 m时,采空区顶板将发生突变失稳。
在同等条件下,选取的最终临界顶板厚度11.34 m与现场安全预警经验值12 m基本一致。露天开采下采空区顶板安全厚度计算模型得到了验证,具有一定的工程应用价值。
4 结 论
(1)基于能量守恒原理和突变理论,推导出由顶板弯曲应变能、水平荷载做功和垂直均布荷载做功组成的露天开采下采空区顶板结构总能量方程。建立了采空区顶板系统尖点突变模型,获得了露天开采下采空区顶板失稳判别式,建立了露天开采下采空区顶板安全厚度计算模型,对研究露天开采下采空区稳定性具有一定的工程指导意义。
(2)根据露天开采下采空区顶板安全厚度计算模型,采空区顶板安全厚度与采空区长度、垂直均布荷载、水平荷载、上覆岩层泊松比、顶板岩梁弹性模量等因素有关。要使采空区顶板保持稳定,应采取措施保证各相关因素在合理安全范围内,确保采空区顶板安全厚度不小于其临界厚度。
(3)运用露天开采下采空区顶板安全厚度计算模型对某露天矿采空区顶板厚度进行计算验证,理论计算出的最终采空区顶板临界厚度为11.34 m,与现场安全预警经验值12 m基本一致。表明建立的采空区顶板安全厚度计算模型合理可行,为露天开采下采空区顶板安全厚度设计提供了理论计算依据。
[1] 王树仁,贾会会,武崇福.动荷载作用下采空区顶板安全厚度确定方法及其工程应用[J].煤炭学报,2010,35(8):1263-1268.
Wang Shuren,Jia Huihui,Wu Chongfu.Determination method of roof safety thickness in the mined-out regions under dynamic loading and its application[J].Journal of China Coal Society,2010,35(8):1263-1268.
[2] 燕恩科,姚国栋,万忠明.露天矿采空区顶板最小安全厚度研究[J].化工矿物与加工,2011,40(5):23-25.
Ye Enke,Yao Guodong,Wan Zhongming.Study of the minimum safety thickness of the underground goaf[J].Industrial Minerals & Processing,2011,40(5):23-25.
[3] 周晓超,侯克鹏.基于改进梁模型的地下空区顶板安全厚度分析[J].矿冶,2014,23(1):21-25.
Zhou Xiaochao,Hou Kepeng.Analysis of roof safety thickness of the underground goaf based on improved beam model[J].Mining & Metallurgy,2014,23(1):21-25.
[4] 林 杭,曹 平,李江腾,等.采空区临界安全顶板预测的厚度折减法[J].煤炭学报,2009,34(1):53-57.
Lin Hang,Cao Ping,Li Jiangteng,et al.The thickness reduction method in forecasting the critical safety roof thickness of gob area[J].Journal of China Coal Society,2009,34(1):53-57.
[5] 张敏思,朱万成,侯召松,等.空区顶板安全厚度和临界跨度确定的数值模拟[J].采矿与安全工程学报,2012,29(4):543-548.
Zhang Minsi,Zhu Wancheng,Hou Zhaosong,et al.Numerical simulation for determining the safe roof thickness and critical goaf span[J].Journal of Mining & Safety Engineering,2012,29(4):543-548.
[6] 邓鹏宏,王海龙.车辆荷载作用下露天矿采空区顶板安全厚度研究[J].金属矿山,2016(3):62-66.
Deng Penghong,Wang Hailong.Study on safety thickness of goafroof under the vehicle load in open-pit iron mine[J].Metal Mine,2016(3):62-66.
[7] 何忠明,彭振斌,曹 平,等.双层空区开挖顶板稳定性的FLAC3D数值分析[J].中南大学学报:自然科学版,2009,40(4):1066-1071.
He Zhongming,Peng Zhenbin,Cao Ping,et al.Numerical analysis for roof stability of double gob area after excavation by FLAC3D[J].Journal of Central South University:Science and Technology,2009,40(4):1066-1071.
[8] 柳小波,安 龙,张凤鹏.基于薄板理论的空区顶板稳定性分析[J].东北大学学报:自然科学版,2012,33(11):1628-1632.
Liu Xiaobo,An Long,Zhang Fengpeng.Analysis on roof stability of gob area based on thin plate theory[J].Journal of Northeastern University:Natural Science,2012,33(11):1628-1632.
[9] 甄云军,陈开翔,刘应发,等.地下采空区顶板安全厚度的确定[J].化工矿物与加工,2007,36(9):19-20.
Zhen Yunjun,Chen Kaixiang,Liu Yingfa,et al.Determination of roof safety thickness for underground mined-out area[J].Industrial Minerals & Processing,2007,36(9):19-20.
[10] 赵 康,鄢化彪,冯 萧,等.基于能量法的矿柱稳定性分析[J].力学学报,2016,48(4):976-983.
Zhao Kang,Yan Huabiao,Feng Xiao,et al.Stability analysis of pillar based on energy law[J].Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):976-983.
[11] 秦四清,王思敬.煤柱-顶板系统协同作用的脆性失稳与非线性演化机制[J].工程地质学报,2005,13(4):437-446.
Qin Siqing Wang Sijing.Instability leading to rockbursts and nonlinear evolutionary mechanisms for coal-pillar-and-roof system[J].Journal of Engineering Geology,2005,13(4):437-446.
[12] 闫长斌,徐国元.动荷载诱发上下交叠硐室间顶柱失稳的突变理论分析[J].工程力学,2007,24(4):46-51.
Yan Changbin,Xu Guoyuan.Analysis on instability of the top pillar between overlap underground chambers induced by danymic loadings with catastrophy theory[J].Engineering Mechanics,2007,24(4):46-51.
[13] 任智敏.基于尖点突变理论的大跨度巷道顶板稳定性分析[J].中国矿业,2014,23(10):111-114.
Ren Zhimin.Stability analysis of large-span roadway roof based on cusp catastrophe theory[J].China Mining Magazine,2014,23(10):111-114.
[14] 张钦礼,曹小刚,王艳利,等.基于尖点突变模型的采场顶板-矿柱稳定性分析[J].中国安全科学学报,2011,21(10):52-57.
Zhang Qinli,Cao Xiaogang,Wang Yanli,et al.Stability analysis of stope roof-pillar based on cusp catastrophe model[J].China Safety Science Journal,2011,21(10):52-57.
[15] 赵延林,吴启红,王卫军,等.基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J].岩石力学与工程学报,2010,29(7):1424-1434.
Zhao Yanlin,Wu Qihong,Wang Weijun,et al.Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(7):1424-1434.
[16] 马 莎,肖 明.基于突变理论和监测位移的地下洞室稳定评判方法[J].岩石力学与工程学报,2010,29(S2):3812-3819.
Ma Sha,Xiao Ming.Judgment method for stability of underground cavern based on catastrophe theory and monitoring displacement[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S2):3812-3819.
[17] 郑东健,雷 霆.基于突变理论的高拱坝失稳判据研究[J].岩土工程学报,2011,33(1):23-27.
Zheng Dongjian,Lei Ting.Instability criteria for high arch dams using catastrophe theory[J].Chinese Journal of Geotechnical Engineering,2011,33(1):23-27.
[18] 杨治林.回采巷道底板岩层结构的后屈曲性态研究[J].煤炭学报,2011,36(S2):278-281.
Yang Zhilin.Post-buckling behavior of floor strata structure for extraction roadway[J].Journal of China Coal Society,2011,36(S2):278-281.
[19] 邵爱军,彭建萍,刘唐生.矿坑底板突水的突变模型研究[J].岩土工程学报,2001,23(1):38-41.
Shao Aijun,Peng Jianping,Liu Tangsheng.Research on a cusp catastrophic model of water bursting in pit floors[J].Chinese Journal of Geotechnical Engineering,2001,23(1):38-41.
[20] 张建文,王树仁,贾会会,等.地面施工载荷对采空区顶板变形破坏效应分析[J].煤炭科学技术,2010,38(9):19-22.
Zhang Jianwen,Wang Shuren,Jia Huihui,et al.Analysis on construction loading at surface ground to roof deformation failure effect in goaf of underground mining[J].Coal Science and Technology,2010,38(9):19-22.
[21] Zhao Wangchun,Wang Tingting,Ju Guoshuai,et al.The study on fractal damage of rock under hydraulic fracturing basing on conversation of energy[J].Applied Mechanics & Materials,2010,29/32:1363-1368.
[22] 罗斌玉,叶义成,胡南燕,等.基于应变能平衡的条带矿柱破裂宽度及其影响因素[J].金属矿山,2016(8):48-53.
Luo Binyu,Ye Yicheng,Hu Nanyan,et al.Width of fractured zone of strip pillars based on the strain energy balance theory and Its influencing factors[J].Metal Mine,2016(8):48-53.
[23] Wang Zhiqiang,Li Aiwu,Pan Yue.Energy Releasing Illustration of Rock Destabilization Based on Catastrophe Theory[J].Advanced Materials Research,2011,261/263:947-951.
[24] 潘 岳,王志强,张 勇.突变理论在岩体系统动力失稳中的应用[M].北京:科学出版社,2008:4-6.
Pan Yue,Wang Zhiqiang,Zhang Yong.Application of Catastrophe Theory to the Dynamic Stability Loss of Rock Mass System[M].Beijing:Science Press,2008:4-6.

