航天器近距离交会的固定时间终端滑模控制
袁 利,马广富,董经纬,李传江,姜博严
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引 言
航天器近距离交会是空间任务中的一项关键技术,如在轨服务、空间拦截以及大型空间结构的组装等,这些任务不仅需要追踪航天器能够快速准确地跟踪并接近目标航天器,且在交会对接的近距离段需要追踪航天器的姿态伴随轨道机动进行同步的机动或跟踪,因此要求对追踪航天器进行六自由度的位姿耦合控制才能完成任务。为了提高此阶段的控制性能,国内外学者针对不同的航天任务提出了很多六自由度位姿控制算法,比如文献[1]提出的非线性PD控制算法,文献[2]基于滑模控制和积分反步法分别设计的控制器,文献[3]提出的基于滑模控制的快速绕飞控制算法等。
但上述的六自由度位姿控制器只能保证航天器位置和姿态渐近稳定,即理论上系统状态只能在无穷的时间内收敛到平衡点。相比之下,有限时间控制方法不仅可以提高系统状态在接近平衡点位置时的收敛速度,而且能在理论上实现系统状态的有限时间内稳定。此外有限时间控制还具有精度高、抗干扰能力强等优点,因此受到广泛的关注并取得了大量的成果。目前有限时间控制器的设计方法大体可以分为三类:即齐次方法[4],加幂积分方法[5-6]和终端滑模方法[7]。相比于前两种方法,终端滑模具有能分析系统鲁棒性,能估算收敛时间上界,且设计过程简单,参数选取自由度大等优点,因此被广泛地应用到航天器控制中[8-10]。但传统终端滑模控制存在奇异问题[11],即随着系统状态收敛或者穿越平衡点,控制输出会显著增大甚至趋于无穷。为了解决该问题,许多能避免奇异的终端滑模面被先后提出,也被用在航天器的控制器中,如非奇异终端滑模[12-13],在奇异点附近切换成线性滑模面的终端滑模(滑模替换法)[14-15],以及两类不同形式的积分终端滑模[16-17]等。这几种非奇异终端滑模虽然都能使控制器避免奇异,但也都存在着不足,比如传统非奇异终端滑模不能估计系统收敛时间上界,滑模替换法中的阈值选取不当可能会导致系统状态最终为渐近收敛,而积分终端滑模又具有齐次方法或加幂积分方法特有的问题等。所以,如何设计非奇异的终端滑模控制器,同时又能解决以上问题,仍值得学者们做进一步的研究。
固定时间稳定是一类特殊的有限时间稳定概念[18],相比于有限时间控制,固定时间控制估计的系统收敛时间上界不依赖于系统初值,即不管系统初始状态是在接近平衡点处还是远离平衡点处,都能保证系统在固定的时间内稳定。此外,相比于快速有限时间稳定[19],固定时间控制器中显式含有大于1和小于1的分数幂,能同时提高系统状态在接近平衡点阶段或远离平衡点阶段的收敛速度,即具有更快的收敛速度。现有固定时间控制器都是基于终端滑模方法(固定时间终端滑模)设计的,其在航天器控制方面的研究成果相对较少,目前也仅有文献[20]针对航天器姿态稳定设计了固定时间控制器。
在以上研究的基础上,本文针对存在空间自由翻滚情形的航天器作为接近目标,主要研究近距离交会段的六自由度位姿控制器设计。该阶段的航天器运动是位姿耦合的,即姿态和位置需要同时控制才能完成交会任务,而固定时间控制具有的双幂次特性能同时提高姿态和位置稳定速度和精度,因此本文基于固定时间稳定概念设计了位姿一体化自适应控制器,其中自适应技术的使用是为了估计未知干扰的上界,以提高系统的抗干扰能力。此外,为了解决终端滑模的奇异问题,本文在传统非奇异终端滑模基础上通过引入切换函数,不仅避免了奇异问题,也使得系统的收敛时间上界可估计,且该时间上界与状态初值无关。
1 航天器运动模型
1.1 航天器相对位置动力学模型
在Hill坐标系中追踪航天器和目标航天器间的的相对运动方程为[21]
(1)
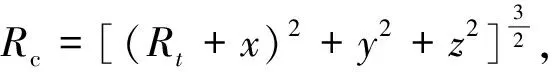
(2)
式中:
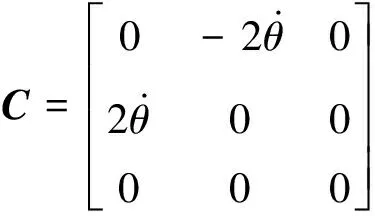
由于航天器推力器是沿着本体进行安装的,故需将本体坐标系中的控制力转到Hill坐标系中,即
(3)
式中:AHc为追踪航天器本体坐标系到Hill坐标系的转换矩阵,AHI为惯性坐标系到Hill坐标系的转换矩阵,AtI为惯性坐标系到目标航天器本体坐标系的转换矩阵,Act为目标航天器本体坐标系到追踪航天器本体坐标系的转换矩阵。
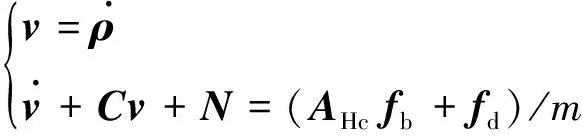
(4)
1.2 相对姿态动力学模型
采用四元数描述航天器姿态,目标航天器在本体坐标系中的姿态动力学方程为
(5)
追踪航天器的姿态动力学方程为
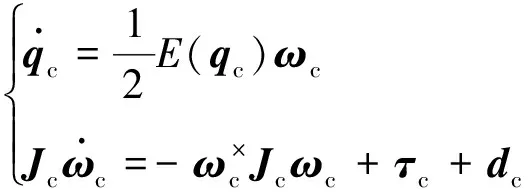
(6)
式中:τc表示追踪航天器的控制力矩,其余各符号定义与目标航天器类似,不再赘述。
追踪航天器相对目标航天器的姿态四元数为

(7)
ωr=ωc-Actωt
(8)
对式(8)求导,有
(9)
根据式(5)、(6)和(9),可得到追踪航天器相对目标航天器的姿态动力学方程为[22]
(10)
1.3 相对位置和姿态一体化模型
(11)

引理1[23].考虑如下非线性系统
(12)
式中:x(0)=0,f(0)=0,x∈Rn。若存在Lyapunov函数V(x),常量α>0,0 (13) 则系统为实际有限时间稳定。 引理2[20]. 考虑式(12)描述的非线性系统,若存在Lyapunov函数V(x),常量α>0,β>0,0 (14) 则系统为实际固定时间稳定,引入正常数θ∈(0,1),则状态会在固定时间内到达平衡点所在的邻域内 (15) 到达时间上界为T 注1. 从式(15)可以看出,固定时间稳定所需的时间上界与系统状态初值无关,且可通过调整控制器参数来设计其值。 针对式(11)给出的相对位置和姿态一体化模型,采用非奇异终端滑模方法进行控制器设计,与传统线性滑模控制相比,非奇异终端滑模控制具有更快的收敛速度以及更高的精度。本文假设航天器所受干扰是未知但有界的,并采用自适应方法对干扰上界进行估计,控制目标是在干扰上界未知的情况下,使相对位置和相对姿态在固定时间内到达期望值。 首先引入非奇异终端滑模面 s=x+sig (ky)1/p1 (16) 式中:k=diag(k1,…,k6),ki=1/(α1|xi|g1-p1+β1),α1,β1,p1,g1均为正常数,且满足1/2 定理1. 考虑式(11)描述的位置和姿态一体化模型,选取非奇异终端滑模面(16),在假设1成立的前提下,控制器(17)能够使航天器相对位置和姿态在有限时间内收敛到包含滑模面s=0的邻域内, u= -G-1(f1k-1A-1y+k-1h+f2)-G-1sgn(s)- G-1k-1A-1diag(με)[α2sig(s)p2+β2sig(s)g2] (17) 式中:f1,G,f2为式(11)中定义的非线性项。为简化控制器形式,定义新的由系统状态表示的辅助变量A和h,具体形式为 A=diag(A1,…,A6),Ai=|kiyi|1/p1-1/p1 h=-α1(g1-p1)diag(sig(x)g1-p1-1)k2diag(f1y)y 其中,α1>0,β1>0,0 (18) 证. 选取如下的Lyapunov函数 (19) (20) 由于控制器和自适应律都是分段函数,为便于稳定性分析,将相平面分成下面两个部分,并分别分析系统状态的运动趋势。 (21) 由于对任意δ>1/2,有下面的不等式成立[25] (22) 故可将不等式(21)写为 (23) 式中:γ=2(p2+1)/2α2,χ=(δγ2/(p2+1))/(2ηδ-η)。 由引理3可得 (24) 由式(24)和引理1可知,si可在有限时间内到达包含si=0的邻域内,或者进入图1所示的Ω2内,该邻域的表达式为 (25) -α2μεi|si|p2+1-β2μεi|si|g2+1 (26) [α2sig(si)p2+β2sig(si)g2] (27) 将式(27)代入一体化模型(11),得到 (28) 定理2. 对于式(11)描述的位置和姿态一体化模型,在假设1和2的前提下选取非奇异终端滑模面(16)和控制器(17),则系统状态能够在固定时间内达到平衡点所在的邻域,且到达时间上限为 T (29) 式中:T1和T2均由控制器参数决定,具体形式在下面的证明过程中给出,t(ε)表示与ε有关的一小段时间。 注2. 控制器中含有两个幂次项,一个的幂次大于1,另一个幂次小于1,故能够在全局范围内加快系统的收敛速度,并提高跟踪精度。 证. 选取Lyapunov函数 (30) 对Vi求导,可得到式(20),然后将相平面分成两个部分进行分析,如图1所示。 (31) 通过变换,可将式(31)写为 (32) (33) (34) 根据式(22)、式(34)以及引理3,不等式(33)变为 (35) 下面给出式(35)能满足引理2中式(14)形式的充分条件。通过引入常数θ∈(0,1),有 (36) (37) (38) 当式(37)或式(38)成立时,式(35)可以写为引理2中式(14)的形式,所以系统状态会在固定时间T1内收敛到D内,或进入Ω2。T1的具体表达式为 T1 (39) 令 ψ=min{ψ1,ψ2} 则区域D可以表示为 D={si|Vi≤ψ} (40) 情况2:当0≤|yi|1/p1-1≤ε,根据定理1中情况2和情况3的分析过程可知,系统轨迹会在有限时间t(ε)内穿过Ω2,此处不再赘述。 上述分析证明了系统会在固定时间内到达滑模面所在的邻域。下面给出到达滑模面后系统状态的变化情况。 (41) 可将式(41)写为 β1sig (xi)p1] (42) (43) (44) 则式(42)可以表示为 (45) 故 T2max (46) T2min (47) 综上,在控制器(17)的作用下,系统能够在式(29)所确定的时间T收敛到平衡点附件所在的邻域内,定理2得证。 注3. 由于正弦函数的存在,系统轨线穿过Ω2时间t(ε)是未知的,但由于ε是一个很小的阈值,故t(ε)有界。 注4. 本文引入正弦函数避免奇异的方法是受文献[26]的启发,但文献[26]只针对一般二阶系统设计固定时间控制器,且干扰上界需假设已知。相比之下,本文针对更复杂的近距离交会位姿耦合模型设计的控制器结合了自适应技术,在干扰上界未知时,依旧可保证系统稳定,更具有应用价值。 本小节对所提出的固定时间终端滑模自适应控制器(17)进行了仿真研究,并与文献[20]中提出的基于一种新的切换滑模面的固定时间控制器进行比较,该滑模面形式如下 Sc=y+Sa (48) 其中 (49) (50) 滑模面中,α3,β3,p3,g3和υ均为大于0的设计参数,且p3υ∈(0,1),g3υ>1,l1=(2-υ)(α3εp3-1/υ+β3εg3-1/υ)υ,l2=(υ-1)(α3εp3-2/υ+β3εg3-2/υ)υ,ε表示切换边界。相应的控制器形式如下 uc= -[α4sig(Sc)p4+β4sig(Sc)g4]+ (51) 自适应更新律为 (52) 仿真中假设目标航天器运行在椭圆轨道上,其轨道参数为at=6.8×106m,et=0.01,θ=0.1 rad,目标航天器的转动惯量Jc为diag(200, 150, 180) kg·m2。追踪航天器的质量m为200 kg,其转动惯量Jt为diag(160, 180, 190) kg·m2,参考文献[27]中干扰形式,选择作用在航天器上的干扰力矩和干扰力分别为: dc=A0[sin(nt),cos(nt),2sin(nt)]T+ D1+G(0,σ1) N·m dt=A0[2sin(nt),-cos(nt),sin(nt)]T+ D1+G(0,σ1) N·m Fd=A0[2sin(nt),-sin(nt),sin(nt)]T+ D2+G(0,σ2) N。 取A0=1.5×10-3,n为航天器的轨道角速度,D1=0.001I3×1和D2=0.01I3×1为由地球引力和大气阻力所引起的扰动,G(0,σ)表示均值为零,方差为σ的高斯白噪声,考虑到航天器交会精度的要求,设σ1=10-6,σ2=10-4。此外,假设陀螺仪的漂移误差为[3 3 3]T(°)/h,测量噪声方差σg=0.01°/h;加速度计的漂移误差为[0.003,0.003,0.003](m/s2),测量噪声方差σa=1.5×10-6m/s2。 仿真中的初始相对位置和相对姿态信息如表1所示,控制器参数如表2所示。 表1 初始位置和姿态信息Table 1 Initial conditions of position and attitude 表2 控制器参数Table 2 Control parameters 由于交会对接过程中对可靠性的要求较高,故仿真中主要对比了控制精度这项指标。图2和图3分别表示追踪航天器和目标航天器之间的相对姿态和相对角速度的变化情况,从图2~3可以看出,在控制器(17)的作用下,相对姿态四元数大约在90 s时收敛到0附近,在100 s时精度达到1×10-3以内,角速度在100 s时小于5×10-4rad/s;在控制器(51)的作用下,相对姿态四元数在100 s附近收敛到0.01内,角速度在20 s时的精度为2×10-3rad/s。图4表示追踪航天器控制力矩的变化情况,控制器(17)输出的最大控制力矩约为0.8 N·m,小于控制器(51)的最大输出力矩1.5 N·m。由仿真结果可知,两个控制器的收敛速度相差不多,但本文所设计的控制器具有更高的控制精度,且输出的控制力矩也更小。 图5和图6分别表示追踪航天器和目标航天器之间的相对位置和相对速度变化情况。从图5~6可以看出,在控制器(17)的作用下,航天器相对位置在150 s时收敛到0.02 m内,相对速度在150 s时达到0.005 m/s以内,能够满足近距离交会等航天任务的需求;在控制器(51)的作用下,航天器相对位置在150 s时在0.2 m附近,相对速度在150 s时约为0.02 m/s,误差仍较大。图7表示追踪航天器的控制力,考虑到执行机构的输出受限,在能较好完成位置跟踪任务的情况下,控制器(17)输出的控制力最大值约为20 N,且很快减小到3 N以内,而控制器(51)输出的最大控制力为30 N,控制代价较大。故本文所设计的控制器能以较小的控制量使追踪航天器跟踪上目标航天器,且具有更高的收敛精度。 在上述仿真的基础上,本文假设采用推力器作为执行机构,并利用脉宽调制(PWM)技术将连续控制信号调制成等效的脉冲信号,在不改变控制参数的前提下分析控制周期对控制器性能的影响。取控制周期T=0.8 s,最小脉冲宽度0.08 s,最大控制力矩0.5 N·m,最大控制力3 N。图8 和图9分别为经过PWM调制后的追踪航天器控制力矩和控制加速度。 图10和图11表示在控制器(17)的连续控制和PWM控制下航天器相对姿态和相对位置的范数变化情况。可以看到,与PWM控制相比,在连续控制信号作用下,航天器的姿态和位置收敛速度更快,且精度更高。 综上仿真分析可知,本文设计的控制器(17)相比于文献[27]中的控制器(51),能使航天器相对位置和姿态以较高的精度更快地收敛到期望值,同时控制量更小。当通过PWM技术将连续控制信号调制成脉冲信号时,本文所设计的控制器仍能保持较好的控制效果。故控制器(17)不仅能够以较小的控制代价使系统状态快速、高精度地收敛到平衡位置,对于干扰具有较强的鲁棒性,同时,也具有一定的工程应用价值。 本文研究了近距离交会过程中追踪航天器对目标航天器位置和姿态跟踪的控制问题,利用固定时间终端滑模方法设计了位姿一体化自适应控制器,并通过切换函数避免了奇异问题,使得系统收敛时间上界可估计,且该时间上界与状态初值无关,然后利用Lyapunov函数给出了稳定性分析,得到系统状态能够在固定时间内收敛到平衡点所在的邻域内。仿真分析中,通过与控制器(51)的对比,本文所设计的控制器具有更快的收敛速度,更高的精度,对干扰有较好的抑制效果,同时控制量也更小。此外,经过PWM调制后,控制器性能仍较好,表明所设计的控制器具有可行性和有效性。 [1] Lee D, Sanval A K, Butcher E A. Asymptotic tracking control for spacecraft formation flying with decentralized collision avoidance [J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 587-600. [2] Kristiansen R, Nicklasson P J, Gravdahl J T. Spacecraft coordination control in 6 DOF: integrator backstepping vs passivity-based control [J]. Automatica, 2008, 44(11): 2896-2901. [3] 朱彦伟, 杨乐平. 航天器快速绕飞任务的六自由度滑模控制研究[J]. 宇航学报, 2009, 30(4):1482-1488. [Zhu Yan-wei, Yang Lei-ping. 6-DOF sliding mode control for fast spacecraft circumnavigation mission [J]. Journal of Astronautics, 2009, 30(4):1482-1488.] [4] Bhat S P, Bernstein D S. Geometric homogeneity with applications to finite-time stability [J]. Mathematics of Control, Signals, and Systems, 2005, 17(2):101-127. [5] Lin W, Qian C J. Adding a power integrator: a tool for global stabilization of high-order lower-triangular systems [C]. The 38th Conference on Decision and Control, Arizona, USA, December 2-7, 1999. [6] Huang X Q, Lin W, Yang B. Global finite-time stabilization of a class of uncertain nonlinear systems [J]. Automatica, 2005, 41(5): 881-888. [7] Man Z H, Paplinski A P, Wu H R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators [J]. IEEE Transactions on Automatic Control, 1994, 39(12): 2464-2469. [8] Dong H Y, Hu Q L, Friswell M I. Dual-quaternion based fault-tolerant control for spacecraft formation flying with finite-time convergence [J]. IEEE Transactions on Control Systems Technology, 2016, 25(4): 1231-1242. [9] 张剑桥, 叶东, 孙兆伟. SE(3)上姿轨耦航天器高精度快速终端滑模控制[J]. 宇航学报, 2017, 38(2):176-184. [Zhang Jian-qiao, Ye Dong, Sun Zhao-wei. High-accuracy fast terminal sliding mode control for coupled spacecraft on SE(3) [J]. Journal of Astronautics, 2017, 38(2):176-184.] [10] Lee D, Vukovich G. Adaptive finite-time control for spacecraft hovering over an asteroid [J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1183-1196. [11] Wu Y Q, Yu X H, Man Z H. Terminal sliding mode control design for uncertain dynamic systems [J]. Systems and Control Letters, 1998, 34(5): 281-287. [12] Meng Z Y, Ren W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies [J]. Automatica, 2010, 46(12): 2092-2099. [13] Lu K F, Xia Y Q. Finite-time fault-tolerant control for rigid spacecraft with actuator saturations [J]. IET Control Theory and Applications, 2013, 7(11): 1526-1539. [14] Xu J. Fault tolerant finite-time leader-follower formation control for autonomous surface vessels with LOS range and angle constraints [J]. Automatica, 2016, 68(C): 228-236. [15] 胡庆雷, 王辉, 石忠, 等. 航天器新型非奇异饱和终端滑模姿态控制[J]. 宇航学报, 2015, 36(4): 430-437. [Hu Qing-lei, Wang Hui, Shi Zhong, et al. Novel non-singular saturated terminal sliding mode based attitude controller for spacecraft [J]. Journal of Astronautics, 2015, 36(4): 430-437.] [16] Jie G, Sheng Y, Liu X. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system [J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976. [17] Tiwari P M, Janardhanan S, Nabi M U. Rigid spacecraft attitude control using adaptive integral second order sliding mode [J]. Aerospace Science and Technology, 2015, 42: 50-57. [18] Polyakov A. Nonlinear feedback design for fixed-time stabilization of linear control systems [J]. IEEE Transactions on Automatic Control, 2012, 57(8): 2106-2110. [19] Yu X H, Man Z H. Fast terminal sliding-mode control design for nonlinear dynamical systems [J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2002, 49(2): 261-264. [20] Jiang B Y, Hu Q L, Friswell M I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults [J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1892-1898. [21] Mai B, Akira I. Periodic orbits of nonlinear relative dynamics and satellite formation [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1200-1208 [22] 廖飞, 季海波, 解永春. 追踪航天器本体坐标系下航天器姿轨一体化控制律设计 [J]. 控制与决策, 2015, 30(9): 1679-1684. [Liao Fei, Ji Hai-bo, Xie Yong-chun. Integrated orbit and attitude control for spacecraft in body fixed coordinate of chaser [J]. Control and Decision, 2015, 30(9): 1679-1684.] [23] Zhu Z, Xia Y Q, Fu M Y. Attitude stabilization of rigid spacecraft with finite-time convergence [J]. International Journal of Robust and Nonlinear Control, 2011, 21(6): 686-702. [24] Du H, Li S, Qian C. Finite-time attitude tracking control of spacecraft with application to attitude synchronization[J]. IEEE Transactions on Automatic Control, 2011, 56(11):2711-2717. [25] Lu K F, Xia Y Q. Finite-time attitude stabilization for rigid spacecraft [J]. International Journal of Robust and Nonlinear Control, 2015, 25(1): 32-51. [26] Zuo Z Y. Non-singular fixed-time terminal sliding mode control of non-linear systems [J]. IET Control Theory and Applications, 2014, 9(4): 545-552. [27] Okasha M, Newman B. Relative motion guidance, navigation and control for autonomous orbital rendezvous[J]. J.Aerosp.Technol.Manag.,2014,6(3):301-318.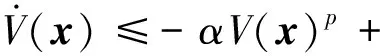


2 控制器设计

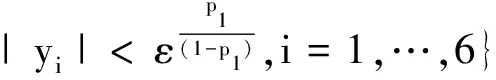







3 仿真校验



4 结 论

