模型参数扰动下的火星大气进入鲁棒状态估计方法

邓剑峰，于正湜

(1. 北京理工大学深空探测技术研究所，北京 100081；2.深空自主导航与控制工业和信息化部重点实验室，北京 100081；3.飞行器动力学与控制教育部重点实验室，北京 100081)

0 引 言

未来火星着陆探测任务要求探测器能在具体特定科学价值的区域实现定点着陆，从而实现最大的科学回报。火星进入、下降、及着陆段(Entry, Descent, and Landing, EDL)的主动制导、导航与控制(GNC)在定点着陆探测中起着重要作用，GNC系统的关键技术之一是在进入过程中精确估计探测器的状态[1]。火星进入过程中大气密度、弹道系数及升阻比等参数的不确定性都会对动力学方程造成扰动，在过载峰值及动压峰值阶段，动力学系统的强非线性会影响状态估计精度[2]。因此，如何有效抑制模型参数扰动对导航系统的影响，保证大气进入过程中系统强非线性条件下探测器的状态估计精度是火星进入高精度自主导航需要解决的难点问题。

为了分析火星大气进入过程中模型参数扰动对状态估计精度的影响，学者提出了一系列方法。广义混沌多项式法(Generalized Polynomial Chaos, GPC)[3]是成功应用于火星进入段模型参数扰动分析及状态估计的方法之一，Prabhakar等[4]研究表明广义混沌多项式能精确预测由初始状态误差、弹道系数、升阻比以及大气密度等参数扰动导致的探测器飞行轨迹随时间的演化。Dutta等[5]结合广义混沌多项式及贝叶斯估计理论对火星大气进入过程中探测器的状态及相关参数进行实时估计。广义混沌多项式方法通过求取确定的常微分方程来近似不确定动力学系统，常微分方程的个数随状态维数及扰动参数个数成指数增长，计算复杂度高。文献[6]中作者通过结合Frobenius-Perron (FP)算子理论和贝叶斯估计理论研究了火星大气进入过程中探测器的状态估计问题。FP方法与粒子滤波(Particle filter, PF)[7]方法类似，都是使用采样点来预测状态的先验概率密度函数随动力学方程的演化，但FP方法相比于粒子滤波需要的样本粒子数更少，因此计算效率相对更高。然而，上述方法由于计算量大，目前只能离线分析模型扰动参数对动力学的影响，并不能在线实时估计火星大气进入过程中探测器的状态信息。

针对上述方法的不足，学者提出了多模型自适应估计(Multiple Model Adaptive Estimation, MMAE)方法及其改进形式来处理火星进入过程中扰动参数对状态估计精度的影响[8-10]。Crassidis等[9]采用多模型自适应估计方法处理(Inertial Measurement Unit,IMU)的标度因子偏差及非校准偏差，从而提高火星进入过程中惯性导航的精度。为了避免求取Jacobi矩阵，肖等人[10-11]提出了多模型自适应秩滤波方法来处理火星大气进入过程中大气密度及气动力参数的扰动对状态估计精度的影响。多模型自适应估计方法固有缺陷在于该方法要求事先已知扰动参数的分布范围，且假设真实模型与模型集中某一模型相同或接近，该方法还存在数值下溢的问题[12]。

不同于多模型自适应估计方法，Karlgaard等人[13-14]借鉴脱敏最优控制(DOC)的思想，通过在传统Kalman滤波方法的代价函数中增加状态误差对扰动参数的灵敏度矩阵的加权积，以小量增加估计误差协方差为代价实现提高导航系统的鲁棒性及状态估计精度。并相继推导了D-EKF[14]，D-UKF[15]，D-DDF[16]。D-EKF可以用于火星大气进入段动力学方程存在模型参数扰动下的状态估计，但该方法需要实时计算动力学方程及测量方程的雅各比矩阵，且在过载峰值及动压峰值阶段估计性能较差[17-18]。D-UKF相比D-EKF可以获得更高的状态估计精度，但该方法可能会导致误差协方差阵出现非正定情况[19]。此外，现有方法的鲁棒估计方法滤波增益都是通数值求解矩阵方程得到，计算量随状态维数及扰动参数个数的增加急剧增大。插值滤波方法通过采用基于斯特灵多维插值公式来近似非线性方程，不需要求取系统的雅各比矩阵，且具有与UKF相同的先验状态估计精度，但是具有更好的滤波稳定性[20-21]。现有的插值滤波方法主要包括一阶插值滤波(DDF1)方法和二阶插值滤波(DDF2)方法，二阶插值滤波方法在动力学系统强非线性的条件下可以获得比一阶滤波方法更高的估计精度。本文在标准插值滤波方法的基础上，通过把状态估计误差对扰动参数的度量矩阵乘积的迹增广到原有代价函数中，推导了具有解析滤波增益形式的鲁棒插值滤波方法。同时，结合在线计算的系统非线性度(Degree of Nonlinearity, DoN)，给出了插值滤波方法阶次自适应选取准则。采用文献[22]提出的系统全局非线性测量方法计算火星进入过程中导航系统的非线性度。

本文的组织如下：第一部分构建了火星进入动力学模型及观测模型，并对动力学系统的扰动进行分析。第二部分介绍随机系统全局非线性测量方法，提出采用秩采样方法求取火星进入过程系统的非线性度。第三部分推导具有闭环解析形式的鲁棒插值滤波方法。最后给出了该鲁棒插值滤波方法在火星大气进入动力学系统存在参数扰动时的状态估计分析。

1 火星进入段导航系统模型建立

1.1 火星进入动力学模型

本文采用简化的进入三自由度动力学模型，进入状态x包括高度h，速度v，航迹角(Flight Path Angle, FPA)γ，方位角ψ，定义指北为零方位角，经度θ，纬度λ，动力学方程如下[23]

(1)

式中μ=4.28283×1013m3/s2为火星引力常数，Rm=3397.2 km为火星半径。σ为倾侧角，假设倾侧角为常值且在整个进入过程中倾侧角没有翻转。阻力及升力加速度D*和L*定义如下

(2)

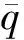
(3)

ρ*表示大气密度，由下式表示[26]

(4)

1.2 火星进入过程观测模型

本部分主要给出火星大气进入过程中目前可用的敏感器及对应的观测模型。在大气进入过程中，目前可用的敏感器主要包括惯性测量单元、压力传感器[27]以及超高频无线电收发机Electra[26-27]。

1)三轴加速度测量

加速度计主要测量火星大气进入过程中作用于探测器上的气动加速度，三轴加速度可表示如下

(5)

式中ak=[-D, -Lsinσ,Lcosσ]T表示进入过程中三轴真实的气动加速度，bk表示加速度计的常值漂移，ηk表示加速度计的零均值高斯白噪声。

2)动压测量

在火星大气进入过程中，探测器周围的动压分布可以由其携带的火星大气数据系统测量得到(Mars Entry Atmospheric Data System, MEADS)，MEADS在“好奇号”任务中首次得到应用[28]。进入过程中，动压观测模型表示如下[29]

(6)

式中vk探测器相对火星大气速度，υq,k表示动压观测噪声。

3)相对距离测量

在火星大气进入段，无线电通信频率超过探测器周围等离子体临界电子密度时，探测器携带的Electra可以通过超高频(UHF)与火星轨道器或火星表面无线电信标实现通信[27]。探测器与轨道器/火星表面信标之间的相对距离可表示为

(7)

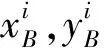
1.3 动力学系统扰动分析

由式(2)-(3)可知，气动阻力和升力加速度与火星大气密度及气动力参数紧密相关。在火星大气进入段，这些参数具有不确定性。火星大气密度的不确定性随高度降低而减小，由进入点附近的60%以上逐渐减少到火星表面的5%左右[30-32]。而探测器气动力系数的不确定性随着马赫数的变化而变化。因此，用于导航的动力学模型中标称参数只能近似描述相关参数的分布。

真实的火星大气密度随高度、位置以及进入时间随机变化，式(4)中指数模型只能近似描述进入过程中火星大气密度分布，真实大气密度可由指数模型值及对应偏差表示

ρ=ρ*(1+Δρ)

(8)

同理，真实弹道系数B及升阻比L/D与标称值之间的关系由下式表示

(9)

Δ表示实际飞行中相应参数的真实值与模型标称值之间的偏差百分比。

由式(2)可知，弹道系数及大气密度对气动加速度的影响是耦合的，定义一个新的参数τ如下

τ*=ρ*B*

(10)

大气密度及弹道系数偏差对参数τ的影响表示如下

τ=ρB=ρ*(1+Δρ)B*(1+ΔB)=τ*(1+Δτ)

(11)

ρ和B分别表示真实的火星大气密度及探测器弹道系数，在实际飞行过程中真实值不能确切知道。Δρ和ΔB表示真实参数与滤波标称值之间的偏差百分比。结合式(2)，由不确定参数引起的动力学扰动可以如下描述：

(12)

式中忽略了2阶及以上小量，通过中间变量τ，动力学中的扰动项可减少为两项。

2 导航系统非线性度量

系统的非线性会直接影响导航状态估计精度，因此，在对导航系统滤波器设计时，必须考虑系统的非线性影响。文献[22]提出的系统全局非线性度量方法基于非线性函数与近似线性函数集距离均方根提出。为衡量火星大气进入过程动力学方程及观测方程对整个导航系统非线性的影响，把动力学方程与观测方程统一成如下联合系统

zk+1=φ(xk)+ηk

(13)

传统的非线性度量方法直接测量非线性函数与其一阶线性近似函数之间的距离，本文采用的非线性度量方法直接求取非线性函数与所有近似线性函数构成的集合之间的最小距离，系统非线性度可以通过求取式(14)的最小值得到[22]：

(14)

zk+1=φ(xk)+ηk

(15)

式中Cφk=cov[φ(xk)]，Cxk=cov[xk]，Cφkxk=cov[φ(xk),xk]。系统全局非线性归一化形式如下：

(16)

由于火星大气进入段动力学系统在过载峰值及动压峰值阶段具有强非线性，本文提出利用秩采样方法来近似求取协方差矩阵Cφk，Cφkxk。秩采样点及对应的权值求取如下[12]：

(17)

3 鲁棒插值滤波方法设计

标准插值滤波方法在动力学及模型参数精确已知的条件下，可以获得较高的状态估计精度，且保证滤波的稳定性。但当动力学系统存在参数扰动时，滤波性能急剧衰减，甚至导致状态估计误差发散[17]。

进入动力学及观测方程的离散形式可表示如下：

xk=f(xk-1,uk-1,wk,α)

(18)

yk=h(xk-1,uk-1,vk,α)

(19)

式中x=[r,v,γ,θ,λ,ψ]T表示维数为nx的状态向量；yk表示观测量，维数为ny；uk表示控制量，wk和vk表示状态维数分别为nv和nw的过程噪声及测量噪声，假设都为零均值高斯白噪声，噪声协方差分别表示为Qk和Rk。变量α=[Δτ, ΔL/D]T表示维数为nl的扰动参数向量。

状态误差协方差及噪声协方差的Cholesky分解表示如下

(20)

(21)

(22)

(23)

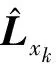
3.1 一阶鲁棒插值滤波方法 (RDDF1)

一阶插值滤波方法采用一阶插值多项式近似非线性方程，动力学方程和观测方程一阶差分矩阵的第i列定义如下[20]：

(24)

(25)

(26)

(27)

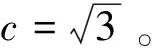
一步预测估计表达式如下

(28)

(29)

(30)

系统新息协方差如下：

(31)

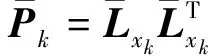
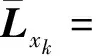
(32)

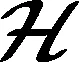
(33)

滤波测量更新方程表示如下：

(34)

(35)

(36)

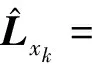
(37)

当动力学系统存在参数扰动时，推导标准一阶插值滤波方法的部分假设条件将不再满足，导致状态估计存在较大偏差甚至发散。在本文中，模型扰动参数对状态估计精度的影响通过状态估计误差对扰动参数的灵敏度矩阵度量。预测/校正状态估计误差的度量矩阵定义如下[15]:

(38)

(39)

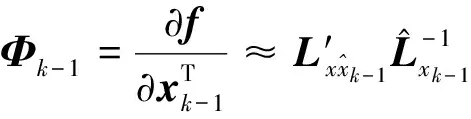
(40)

类似于标准插值滤波方法采用最小化误差协方差的迹来定义代价函数，本文采用状态对所有扰动参数的灵敏度矩阵乘积的迹来衡量扰动参数对状态估计精度的影响，并构建新的代价函数如下：

(41)

式中Wk是一个nl×nl对称半正定加权矩阵，可以随时间变化，矩阵的维数与扰动参数的个数相同。

求取式(41)对滤波增益Kk的偏导数，结合式(38)、(39)可得

(42)

令式(42)等于零，可求得具有解析形式的滤波增益:

(43)

由上式可知，本文所提方法得到的滤波增益具有闭环解析形式，大大减少了计算量。当加权矩阵Wk=0时，滤波增益与标准一阶插值滤波增益具有相同的表达形式。

3.2 二阶鲁棒插值滤波方法(RDDF2)

二阶插值滤波方法利用二阶差商来近似非线性方程，可以获得对非线性方程高阶近似。动力学方程和观测方程二阶差分矩阵的第i列定义如下[22]：

(44)

(45)

(46)

(47)

如式(18)、(19)所示，在火星进入过程中，过程噪声与量测噪声都为零均值线性加性噪声，二阶插值滤波方法一步预测值可由式(48)-(50)求得：

(48)

(49)

(50)

系统新息协方差矩阵表示如下：

(51)

同理，可求得二阶插值滤波状态预测误差协方差和残差协方差的Cholesky分解式如下

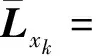
(52)

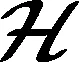
(53)

二阶插值滤波测量更新方程与一阶插值滤波形式相同，如式(34)-(35)所示，且滤波增益由最小化代价函数(41)求得。因此，二阶鲁棒插值滤波方法具有与一阶鲁棒插值滤波方法相同的闭环滤波增益。但是，二阶鲁棒插值滤波方法中状态估计误差对扰动参数的度量矩阵形式更为复杂，由于扰动参数与系统噪声不相关，故系统噪声及噪声协方差的Cholesky分解项对扰动参数的敏感度为零，扰动参数对一步预测状态估计误差的度量矩阵可由式(48)求得：

(54)

状态估计误差对扰动参数的灵敏度矩阵与式(39)形式相同，其中：

(55)

式(54)中动力学方程对状态的偏导数的简化表达式如下

(56)

式(55)中的偏导数的缩略形式与式(56)类似。

(57)

(58)

由式(50)及噪声协方差与扰动参数不相关可得：

(59)

状态一阶差分及二阶差分矩阵的第i列向量对扰动参数αj的偏导数可结合式(24)及式(44)求得：

(60)

(61)

(62)

式中

(63)

式(63)中右边差分矩阵对扰动参数的偏导数可分别由式(26)和式(46)求得。

(64)

(65)

3.3 自适应阶次鲁棒插值滤波方法 (ARDDF)

当系统非线性较弱时，一阶鲁棒插值滤波方法和二阶鲁棒插值滤波方法的状态估计精度差异不大，而二阶鲁棒插值滤波方法的计算量大。在火星大气进入过程中，动力学仅在过载峰值及动压峰值阶段呈现强非线性。为保证状态估计精度及导航系统的解算速度，结合上述推导的一阶及二阶鲁棒插值滤波方法，以及第二部分系统给出的系统非线性度量方法，给出自适应阶次鲁棒插值滤波方法，具体实施过程如下：

步骤1：根据文中第二部分系统非线性度量方法计算整个系统的全局非线性度；

步骤2：对比步骤1所求系统全局非线性度与给定阈值DoNT，当系统非线性度小于或等于给定阈值时，导航系统选定一阶鲁棒插值滤波方法，否则，采用二阶鲁棒插值滤波方法。

步骤3：根据步骤2选定的插值滤波方法估计火星大气进入过程探测器的状态信息，令k=k+1，跳转步骤1。

很显然，根据本文提出的阶次选取原则，只有当导航系统非线性度大于给定阈值时，自适应阶次鲁棒插值滤波方法才选取二阶鲁棒滤波方法，非线性度阈值可以根据导航方案设计任务对状态估计精度及导航解算时间确定。

4 仿真校验

在仿真分析中，假设火星大气进入过程持续时间为400秒，仿真步长为0.2秒，采用4阶龙格-库塔法作为动力学方程积分器，本文采用MATLAB 2016a作为仿真工具，仿真采用的电脑配置为3.60 GHz Intel Core i7-4790四核处理器和4G RAM。

表1 仿真初始状态Table 1 Initial states for simulation

表2 火星轨道器的轨道参数Table 2 Parameters of the Mars orbiter

一阶、二阶鲁棒插值滤波方法以及本文提出的基于系统非线性度自适应阶次鲁棒插值滤波方法状态估计误差如图2所示，Y轴取以十为底的对数，其中加权矩阵假设为Wk=diag(0.5, 0.01)。黑色虚线代表一阶鲁棒插值滤波方法(RDDF1)、蓝色实线表示二阶鲁棒插值滤波方法(RDDF2)、红色点画线表示本文所提自适应阶次鲁棒估计方法(ARDDF)。由图可知，自适应阶次鲁棒插值滤波方法比一阶鲁棒插值滤波方法状态估计精度更高(参见网站彩色电子版图)，尤其是在过载峰值和动压峰值阶段的速度估计，整体状态估计精度与二阶鲁棒插值滤波方法估计性能相近。

方法时间RDDF10．8917sRDDF218．5218sARDDF6．5316s

三种滤波方法的平均每次运行时间如表3所示。显然，采用ARDDF滤波方法比整个火星进入过程采用二阶鲁棒插值滤波方法运行时间更短，解算效率提高一倍以上。图2为自适应阶次鲁棒插值滤波方法阶次变化，在整个火星大气进入过程中，只有在进入初始阶段及过载峰值及动压峰值阶段采用二阶鲁棒插值滤波方法。图3展示了进入过程中导航系统的非线性度随时间的变化曲线。因为初始进入状态偏差较大，秩采样点分布范围较大，导致在线计算的非线性较强，而过载峰值阶段由于气动力的剧烈变化导致系统强非线性。仿真中系统非线性的阈值假设为0.0002，阈值的大小直接决定了自适应策略对鲁棒插值滤波方法阶次的选取。

图4和图5分析了自适应阶次鲁棒插值滤波方法中不同阈值条件下导航系统的状态估计精度及对应滤波阶次的变化。由图4可知，不同的阈值对状态估计精度的影响较为明显，尤其对速度的估计。当系统非线性度阈值较大时，自适应阶次鲁棒插值滤波方法选取二阶插值滤波方法的时间较短，计算效率高，在过载峰值段探测器状态估计精度较低；反之，系统非线性度阈值较小时，采用二阶鲁棒插值滤波方法的时间较长，计算效率较低，但状态估计精度较高。图5展示了三种不同阈值条件下对应的滤波阶次变化，很显然，当阈值为0.00015时，选取二阶鲁棒插值滤波的时长占火星整个进入过程的一半左右，对应于图4中导航状态估计精度最高。阈值的大小直接影响了系统的解算效率及导航系统状态估计精度。因此，可以根据探测任务对导航精度的要求及星载计算机的解算能力合理确定系统非线性度的阈值，保证自主导航的实时性和状态估计精度。

5 结论

本文提出把扰动参数对状态估计精度影响的度量矩阵乘积的迹增广为代价函数，推导了具有解析滤波增益形式的一阶及二阶鲁棒插值滤波方法，克服了模型参数扰动导致火星大气进入状态估计发散的难题。同时引入系统非线性度，给出了自适应阶次鲁棒插值滤波方法，在系统非线性弱时选取一阶鲁棒插值滤波方法，在系统强非线性时选取二阶鲁棒插值滤波方法。既保证了进入过程中导航系统状态估计精度，同时降低了计算量，能满足火星大气进入过程导航实时性需求。

[1] Braun R D, Manning R M. Mars exploration entry, descent, and landing challenges [J]. Journal of Spacecraft and Rockets 2007; 44(2):310-323.

[2] 崔平远, 于正湜, 朱圣英. 火星进入段自主导航技术研究现状与展望 [J]. 宇航学报 2013; 34(4):447-456. [Cui Ping-yuan, Yu-Zheng-Shi, Zhu Sheng-ying. Research progress and prospect of autonomous navigation techniques for mars entry phase [J]. Journal of Astronautics, 2013; 34(4):447-456.]

[3] Xiu D, Karniadakis G E. The Wiener-Askey polynomial chaos for stochastic differential equations [J]. SIAM Journal on Scientific Computing 2002; 24(2):619-644.

[4] Prabhakar A, Fisher J, Bhattacharya R. Polynomial chaos-based analysis of probabilistic uncertainty in hypersonic flight dynamics [J]. Journal of Guidance, Control, and Dynamics 2010; 33(1):222-234.

[5] Dutta P, Bhattacharya R. Nonlinear estimation of hypersonic state trajectories in Bayesian framework with polynomial chaos [J]. Journal of Guidance, Control, and Dynamics 2010; 33(6):1765-1778.

[6] Dutta P, Bhattacharya R. Hypersonic state estimation using the Frobenius-Perron operator [J]. Journal of Guidance, Control, and Dynamics 2011; 34(2):325-344.

[7] Arulampalam M S, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking [J]. IEEE Transactions on signal processing 2002; 50(2):174-188.

[8] Dubois-Matra O, Bishop R. Multi-model navigation with gating networks for Mars entry precision landing [C]. AIAA Atmospheric Flight Mechanics Conference and Exhibit. Providence, USA, August 16-19, 2004.

[9] Marschke J M, Crassidis J L, Lam Q M. Multiple model adaptive estimation for inertial navigation during Mars entry [C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Hawaii, USA, August 18-21, 2008.

[10] Xiao Q, Fu H M, Wang Z H, et al. Multiple model adaptive rank estimation for integrated navigation during Mars entry [J]. The Journal of Navigation 2016:1-18.

[11] 傅惠民, 肖强, 吴云章, 等. 秩滤波方法 [J]. 机械强度 2014; 36(4):521-526. [Fu Hui-min, Xiao Qiang, Wu Yun-zhang, et al. Rank filter method [J]. Journal of Mechanical Strength, 2014; 36(4):521-526.]

[12] Chaer W S, Bishop R H, Ghosh J. A mixture-of-experts framework for adaptive Kalman filtering [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 1997; 27(3):452-464.

[13] Karlgaard C, Shen H. Desensitized optimal filtering [C]. AIAA Guidance, Navigation, and Control Conference, Portland, USA, August 08-11, 2011.

[14] Karlgaard C D, Shen H J. Desensitised Kalman filtering [J]. IET Radar, Sonar & Navigation 2013; 7(1):2-9.

[15] Shen H J, Karlgaard C D. Desensitized unscented Kalman filter about uncertain model parameters [C]. Institute of Navigation International Technical Meeting, Newport Beach, California, USA. 2012.

[16] Karlgaard C D, Shen H J. Robust state estimation using desensitized divided difference filter [J]. ISA Trans 2013; 52(5):629-637.

[17] Wang L S, Xia Y Q. Mars entry navigation with uncertain parameters based on desensitized extended Kalman filter [J]. IEEE Transactions on Industrial Informatics 2015; 11(5):998-1005.

[18] Lou T S, Zhao L Y. Robust Mars atmospheric entry integrated navigation based on parameter sensitivity [J]. Acta Astronautica 2016; 119:60-70.

[19] Van Der Merwe R, Wan E A. Efficient derivative-free Kalman filters for online learning [C]. ESANN. Bruges, Belgium, April 25-27, 2001.

[20] NøRgaard M, Poulsen N K, Ravn O. New developments in state estimation for nonlinear systems [J]. Automatica 2000; 36(11):1627-1638.

[21] Ahmadi M, Khayatian A, Karimaghaee P. Attitude estimation by divided difference filter in quaternion space [J]. Acta Astronautica 2012; 75:95-107.

[22] Liu Y, Li X R. Measure of nonlinearity for estimation [J]. IEEE Trans Signal Processing 2015; 63(9):2377-2388.

[23] Vinh N X, Busemann A, Culp R D. Hypersonic and planetary entry flight mechanics [J]. NASA STI/Recon Technical Report A 1980; 81.

[24] Lévesque J F, Lafontaine J D. Innovative navigation schemes for state and parameter estimation during Mars entry [J]. Journal of guidance, control, and dynamics 2007; 30(1):169-184.

[25] Gazarik M J, Wright M J, Little A, et al. Overview of the MEDLI project [C]. 5th International Planetary Probe Workshop, Bordeaux; France, June 23-29, 2007.

[26] Lightsey E G, Mogensen A E, Burkhart P D, Ely T A, Duncan C. Real-time navigation for Mars missions using the Mars network [J]. Journal of Spacecraft and Rockets 2008; 45(3):519-533.

[27] Morabito D. The spacecraft communications blackout problem encountered during passage or entry of planetary atmospheres [R]. IPN Progress Report 2002:42-150.

[28] Dutta S, Braun R D. Statistical entry, descent, and landing performance reconstruction of the Mars science laboratory [J]. Journal of Spacecraft and Rockets 2014; 51(4):1048-1061.

[29] Karlgaard C D, Beck R E, O’Keefe S A, et al. Mars entry atmospheric data system modelling and algorithm development [C]. The 41st AIAA Thermophysics Conference, San Antonio, USA, June 22-25, 2009.

[30] Spencer D A, Braun R D. Mars Pathfinder atmospheric entry-trajectory design and dispersion analysis [J]. Journal of Spacecraft and Rockets 1996; 33(5):670-676.

[31] Justus C, Duvall A, Johnson D. Mars global reference atmospheric model (Mars-GRAM) and database for mission design [C]. Mars Atmosphere Modeling and Observations, Granada; Spain, January 13-15, 2003.

[32] 崔平远, 胡海静, 朱圣英. 火星精确着陆制导问题分析与展望 [J]. 宇航学报 2014; 35(3):245-253. [Cui Ping-yuan, Hu Hai-jing, Zhu Sheng-ying. Analysis and prospect of guidance aspects for Mars pecision landing [J]. Journal of Astronautics, 2014; 35(3):245-253.]