敬畏数学
袁诚+郭宏彬

【中图分类号】G633.3 【文献标识码】A 【文章编号】2095-3089(2018)02-0110-03
我对数学的钟爱,是从什么时候开始的呢?
大概三四岁的时候,我比较喜欢玩弄一台破旧的计算器。当时完全把一个个数字当成一场场游戏,我不知不觉地对各个数字毫无知觉的进行加减乘除。
有一天,妈妈想逗逗我,便问我“99×99等于几?”四岁的我脱口而出:“9801。”妈妈最开始以为我在开玩笑,然而当她用计算器验证后大吃一惊,又紧接着问:“98乘以98?”“9604”。“66乘以66?”“4356”……妈妈不知为何,脸上乐开了花。
……
我对数学的天赋便被挖掘出来。
……
十三年过去了,我对数学的热爱丝毫不减。在繁重的学习中,也时不时写一些数学演草。这不是作业,却是一个让我快乐的方式。同样,每次的大考,数学都会给我带来惊喜。2017年信阳市数学聯考中,我作为信阳高中普通班的一名学生,数学取得了全市唯一的满分!我意识到数学成为了我的名牌。
数学真的很难学吗?是的,数学真的很难。
我共有几本数学资料?一本。并且是学校发的。如果学校不作要求,我将一本资料也不用。
最好的资料是什么?课本。
一、重视课本
多数人的课本几乎没翻过,却抱着一本本额外资料如饥似渴。难怪成绩上不去,基础不牢,地动山摇!课本上的知识是解题的基础。都说茶壶里煮饺子——有货倒不出,但是连货都没有,又怎么能倒出货呢?
以下几例道出一个事实:对数学的感悟不强,只怪不看课本。
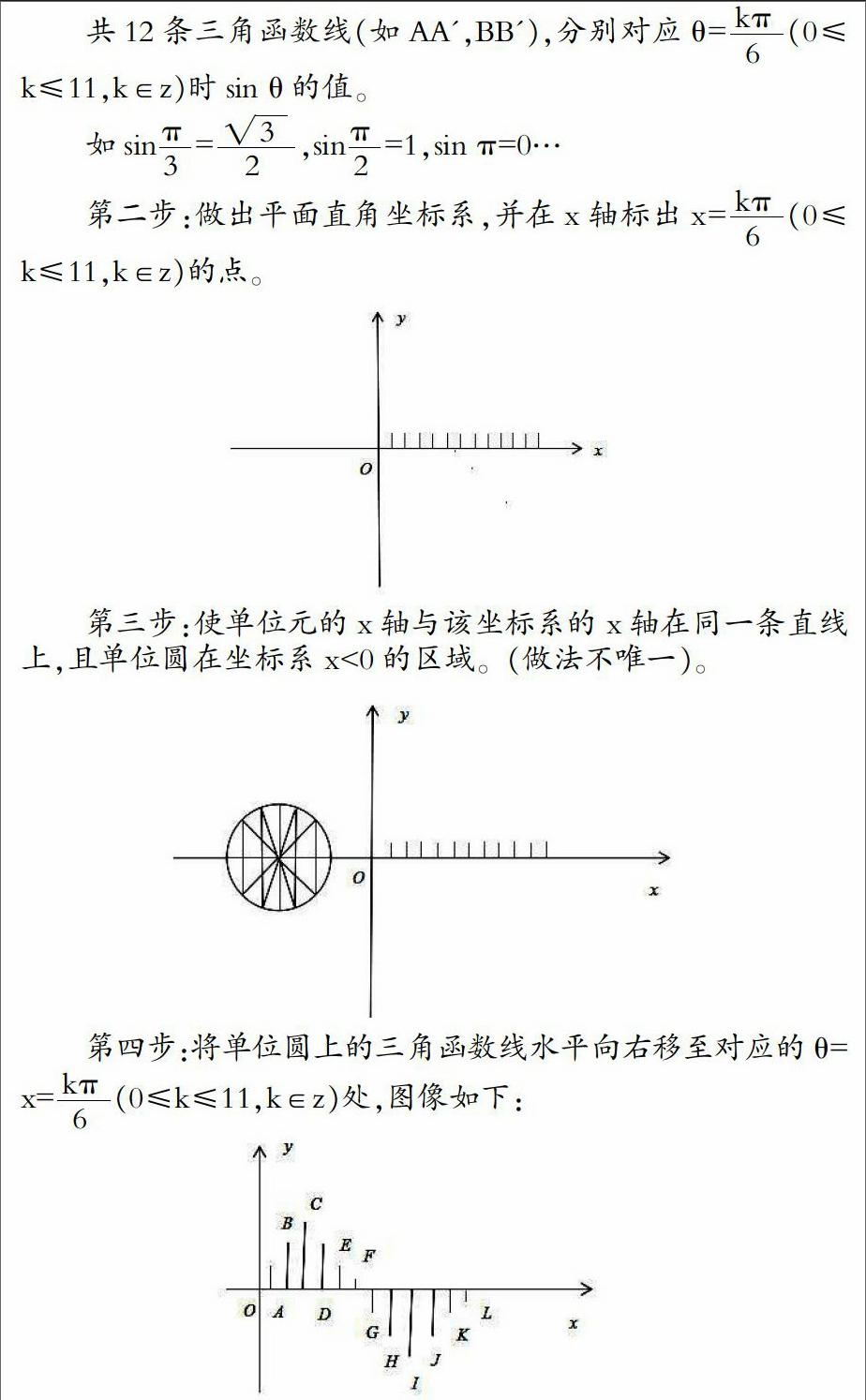
例1:几何法作y=sin x的图像的方法。
多数人不假思索的回答:当然是五点作图法!我的资料对五点作图法的介绍很详细!随便来问。
☆恭喜你们,离谱的错了。而这个问题的根源,还是回归教材《数学4》。
第一步:做出三角函数线:
这道课本习题看似简单,但是蕴含了丰富内涵:
①需要精确找出本题的切入点。
②需要利用对数运算公式进行计算。
这也正符合了高考命题趋势,简明的题干蕴含着综合的能力。课本习题也迎合了这种趋势。一个字:妙!
再看一例,《数学五》课本例题:是否存在边长为连续正整数的三角形,使最大角是最小角的两倍?
这道题的题干简明扼要,可一旦着手计算这道题,就会发现这道题的分量。请认真阅读本题剖析,你会有所提高。
不妨先画出简图如下:
由图可以设出AB
由(20)式,可得sin A=sin 2C,即sin A=2cos C sin C,即■=2cos C(21),■可用含k的代数式表示(正弦定理),cos C也用含k的代数式表示(余弦定理),可列出等式:
■=2×■(22),
由(22)式,易求k=4,所以三角形三边长为4,5,6。
综合分析一下本题的考点:
(i)大边对大角的性质
(ii)正弦定理
(iii)余弦定理
(iv)二倍角公式。
而题干有几个字呢?我只能再次佩服编写课本的专家老师们。
以上聊了聊课本的重要性和如何利用课本。课本是基石,我们应该将投入到各式各样的教辅资料上的精力投入到翻课本中。再强调一遍:课本是最好的资料!
再简单地聊一聊思维与数学:
数学和思维是不可或缺的。但是,并不是每道压轴题都需要极强的思维。有些人一见到压轴题想都不想就进行高思维强度训练,这样极可能得不偿失!我认为,在数学学习中,( )> 基础>思维。
基础和课本唇齿相依,在之前已经详述。如何培养思维?可以从以下几方面着手,但不必太认真,毕竟思维并不是决定数学学习的主要因素,只是一个有利条件。
①尽量多接触和数学有关的事物,培养数学的敏感。
②多和同学讨论数学话题。
③尽可能接触数学古代文化。
④多和数学老师交谈。
而( )处应该填什么?什么能超过思维?甚至超过基础?我认为这就是——作图观。是否具有作图的观念,决定了你的数学素养和能力。

