图的Wiener指数的逆区间

胡 鹏，邵燕灵，刘 奇

(中北大学 理学院， 太原 030051)

1 背景

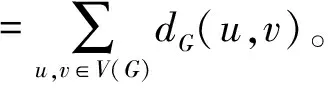
Wiener指数是一种基于分子距离的重要的拓扑指数，它能较好地反映化合物分子结构和物理化学性质之间的联系。因此，为了人工合成所需要的具有某种性质的化合物，人们可以通过刻画具有一定 Wiener指数值的分子图，进而根据分子结构进行合成。基于化合物分子图的Wiener指数与其化学性质之间的密切关系，1995年Gutman和Yeh[1]提出研究连通图Wiener指数的最大逆区间问题。所谓n阶图的Wiener指数的最大逆区间问题是指：寻找一个长度最大的正整数区间[a,b]，使得对于该区间内任意正整数c，均存在一个n阶连通图G使其Wiener指数为c。

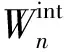
本文主要研究n阶简单连通图G的Wiener指数的最大逆区间问题，将2016年Matjaž Krnc和Ristekrekovski提出的Wiener指数逆区间从蒲公英图延伸到双星图。

2 相关引理

用Kn、Pn、Sn-1分别表示n阶完全图、路图、星图。在文献[13]中定义了n阶蒲公英图D(n,b)，它是将一个星图Sn-b的中心点(记为v0)与一个路图Pb的某一个端点合并成一点得到的n阶图，其中b是一个正整数，且2≤b≤n-2。如果b=2,则D(n,b)即是星图Sn-1。图1是蒲公英图D(17,8)。

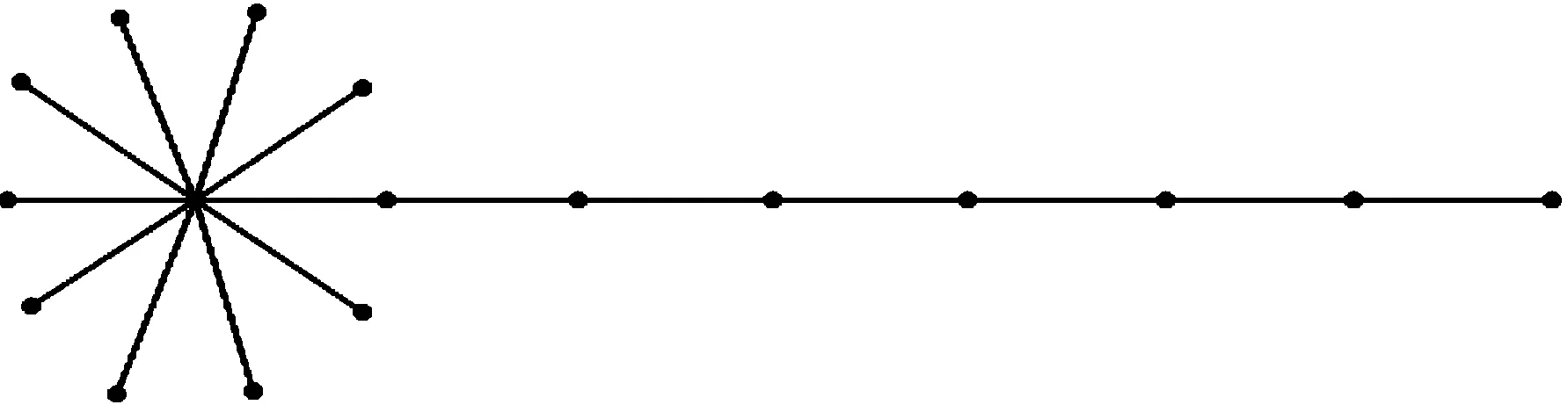
图1 蒲公英图D(17,8)

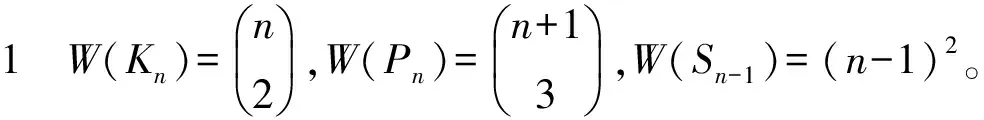
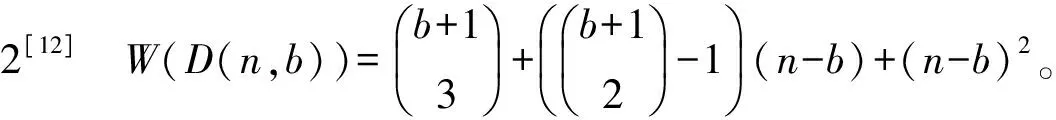
引理4[12]Kn～Sn-1。

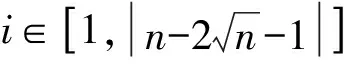
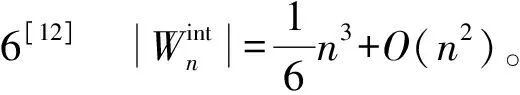
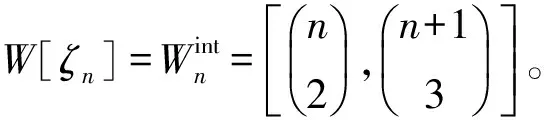
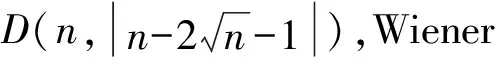
3 主要结论

下面定理1表明，当n≤16时，引理5的结果可以被改进。

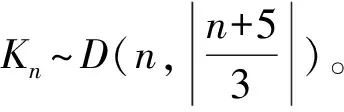
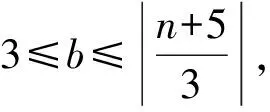
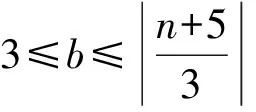
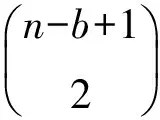
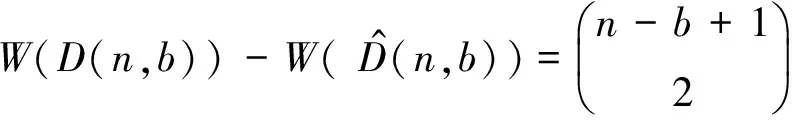
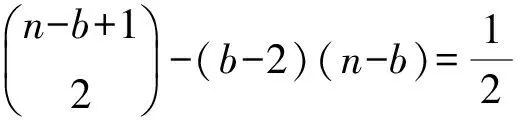
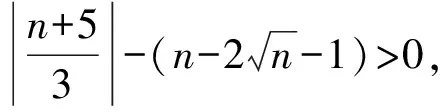
下面考虑文献[12]中定义的图P(a1,…,ak)，它是在路Pk的k个顶点上依次分别粘贴a1,a2,…,ak个悬挂点得到的图，其中k≥1，ai≥0,i=1,2,…,k。由此引出以下的n阶双星图、三星图及四星图。

在P(a1,…,ak)中，若a2=…=ak-1=0，a1=a≥2，ak=b≥2，k=n-a-b，称这样的图为n阶双星图，记为G(n;a,b)。不难看出，双星图G(n;a,b)是分别将星图Sa，Sb的中心点与路图Pn-a-b的两个端点粘贴而成，如图2所示。

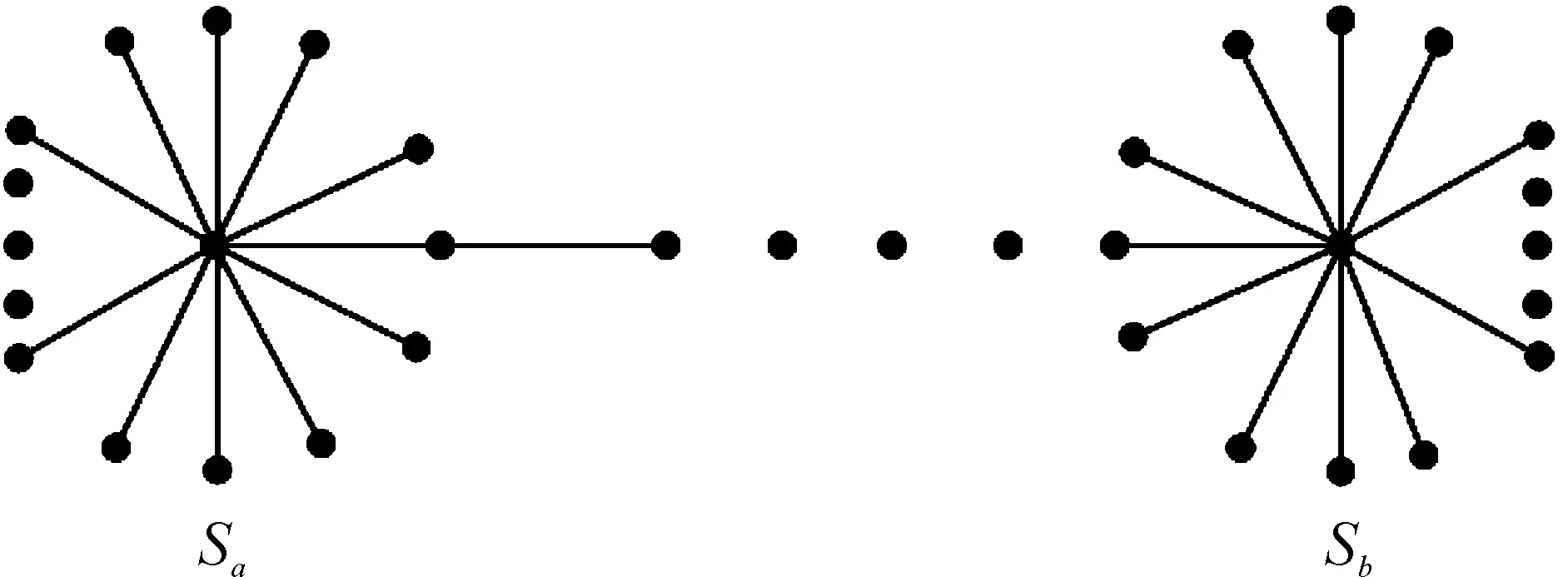
图2 双星图G(n;a,b)

n阶三星图G(n;r,s,t)指在P(a1,…,ak)中，令a3=…=ak-1=0，a1=r，a2=s，ak=t，k≥3，记为三星图G(n;r,s,t)，如图3所示。显然，当s=0时，三星图退化为双星图，即G(n;r,0,t)=G(n;r,t)。

图3 三星图G(n;r,s,t)

n阶四星图G(n;p,q,r,t)是在P(a1,…,ak)中，令a3=…=ak-2=0，a1=p，a2=q，ak-1=r，ak=t，k≥4，如图4所示。

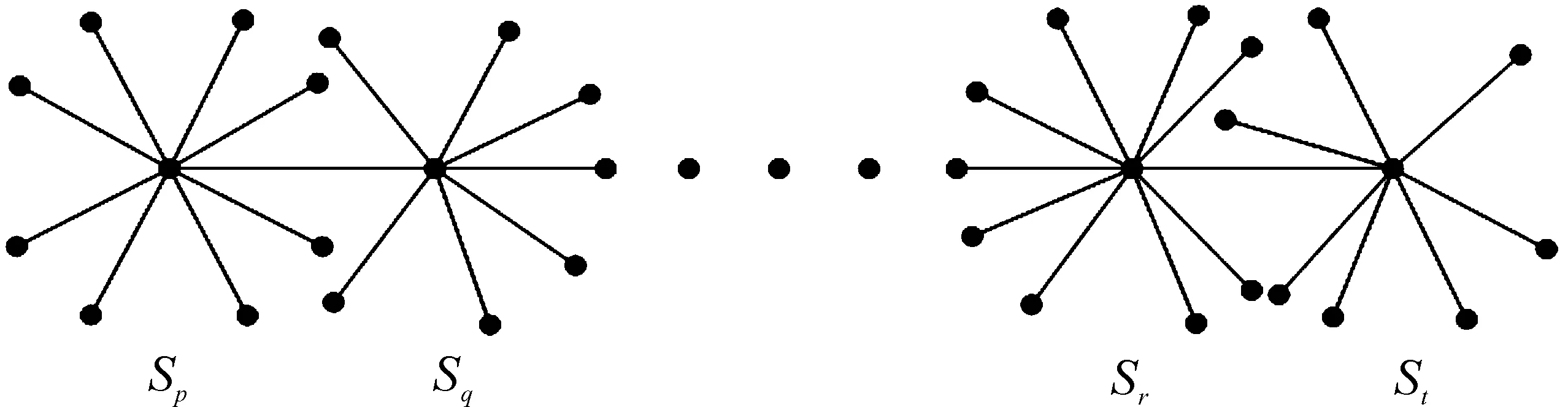
图4 四星图G(n;p,q,r,t)

引理8 设G=G(n;a,b)如图2所示，则

证明由图2可得：

(1)

因为

代入式(1)合并整理得

证明完毕。

证明注意到W(G(n;r+1,s-1,t))-W(G(n;r,s,t))=s-1-r+n-r-s-2 =n-2r-3。

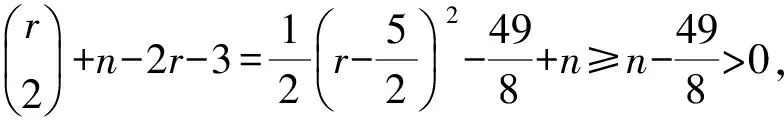
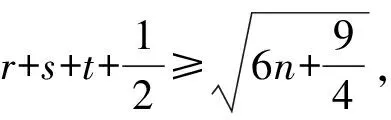
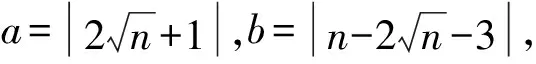
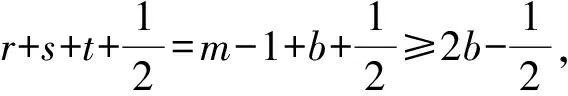
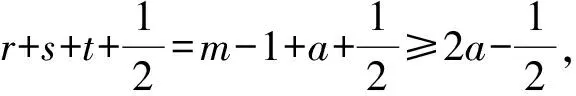
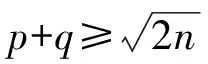
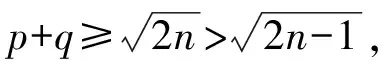
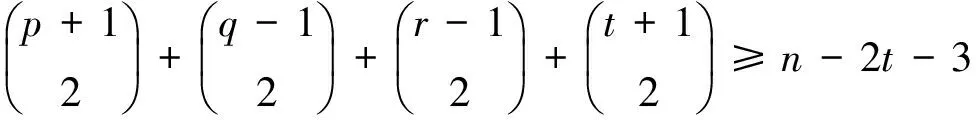
因此，G(n;p+1,q-1,r,t)～G(n;p+1,q-1,r-1,t+1)。

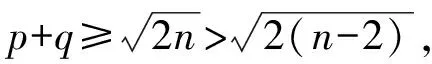
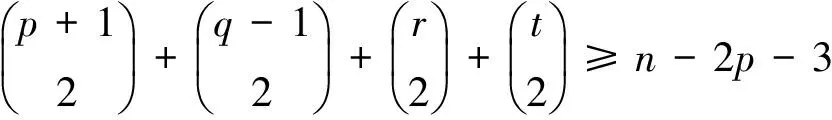
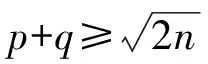
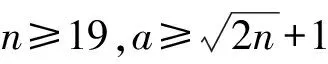
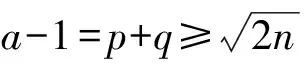
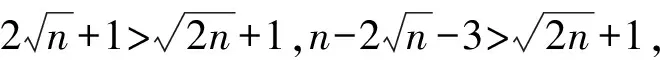
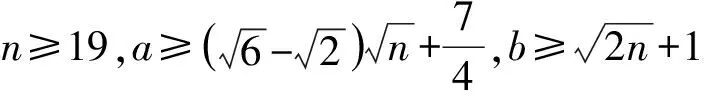
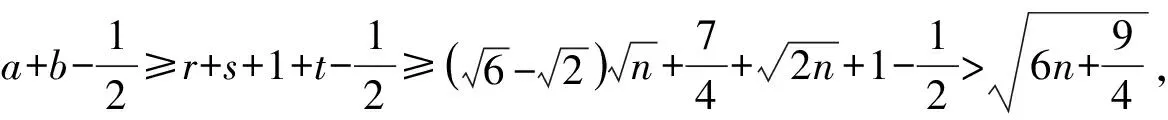
根据本节的引理与推论，得出本文的主要结论：

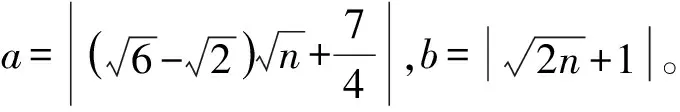
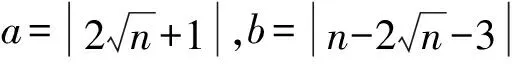
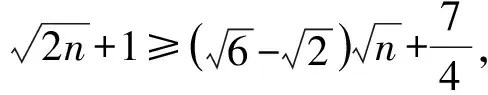
下面计算表明，当n≥86时，定理2的结论改进了引理5的结论。

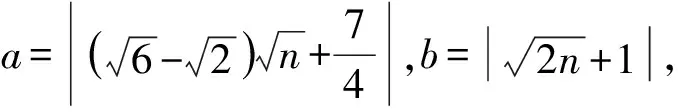
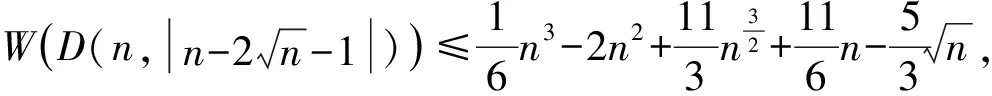
[1] GUTMAN I，YEH Y N.The sum of all distances in bipartite graphs[J].Math Slovaca，1995，45:327-334.

[3] GOLDMAN D，ISTRAIL S，LANCIA G，et al.Algorithmic strategies in combinatorial chemistry[R].USA:Society for Industrial and Applied Mathematics Philadelphia，2000:275-284.

[4] WAGNER S.A Class of trees and its wiener index[J].Acta Appl Math，2006,9l(2):119-132.

[5] WANG H，YU G.All but 49 Numbers ale Wiener Indices of Trees[J].Acta Appl Math，2006，92(1):15-20.

[6] BAN Y A，BESPAMYATNIKH S，MUSTAFA N H.A conjecture on wiener indices in combinatorial chemistry[J].Algorithmica,2004，40(2):99-117.

[7] BEREGA S，WANG H.Wiener indices of balanced binary trees[J].Discrete Applied Mathematics,2007，155(4):457-467.

[8] CZABARKA É，SZÉKELY L，WAGNER S.The inverse problem for certain tree parameters[J].Disc Appl Math,2009，157(15):3314-3319.

[9] LI X L，WANG L.Solutions for two conjectures on the inverse problem of the Wiener index of peptoids[J].SIAM J Disc Math,2004，17(2):210-218.

[10] WAGNER S，WANG H，YU G.Molecular graphs and the inverse Wiener index problem[J].Disc Appl Math，2009，157(7):1544-1554.

[11] FINK J，LUŽAR B，KREKOVSKI R.Some remarks on inverse Wiener index problem[J].Disc Appl Math，2012,160:1851-1858.