基于蒙特卡洛模拟的源网非同调的电网简化方法
张双梅,王国城,刘瑞超(.国网天津市电力公司 宝坻供电分公司,天津 30800;.光大生物能源(天津蓟县)有限公司,天津 30907)
0 引 言
电力系统源网间的协同调控问题是电力系统安全、经济、可靠运行的核心问题。然而,由于系统运行的不均匀性[1-2],导致了源网非同调现象的产生,该现象是指网的安全制约了最经济源的运行,使部分网不随源而变化或变化趋势相反的现象。随着电力系统的发展,风、光、储等可再生能源以分散或集中的方式大规模的并入电网,源的类型、网的规模空前庞大和复杂,导致该现象将进一步加剧。
与此同时,等值简化对异常复杂的电力系统显得尤为必要[3-4],简单且精确的模型可以极大地提高系统的计算效率。近年来,国内外专家学者对此展开了大量的研究[5-6],在动态等值中,同调机群识别、电动机、发电机、原动机等参数简化一直是研究的热点。静态等值中的系统结构分区、网络等值简化等方面也出现了大量的研究成果[7-8]。但这些方法或仅对某一特定元件参数或仅对系统网络结构展开研究,没有考虑源网间的非同调关系,且简化后的等效模型存在依赖于运行点、网络潮流模式变化较大等问题[9-10]。
针对上述情况,本研究提出源网同调和非同调的指标、判别源网同调的方式,以及利用源网同调特点实现电网分类简化的方法。
1 源网非同调现象
根据功率分布理论,电网中任意支路中的潮流为具有不同系数的电源提供的功率分量的代数和,功率分量的归属电源明确,体现了源网之间的耦合关系。然而,对应负荷曲线中某点,电源最经济运行方式受网的制约而出现非同调的现象。本研究采用三节点系统对此情况进行说明,如图1所示。

图1 三节点系统
系统负荷运行模式如表1所示。

表1 负荷运行模式(单位:MW)
1.1 源网同调
在负荷模式一情况下,对其进行连续潮流计算,得到系统各电源及网络潮流变化情况如表2所示。负荷最大时系统运行如图2所示。此时恰好满足网的制约(支路1-2达输电限值)。
结果显示,在该负荷模式下,随着负荷的增加,源网保持同步增加,源的最经济运行方式不受网的制约,源网同调。

表2 负荷模式一下系统有功变化情况(单位:MW)
1.2 源网非同调
在负荷模式二下,节点1、节点3处的负荷保持不变,节点2处的负荷由60 MW增长至116 MW,对其进行连续潮流计算,可得系统各电源及网络潮流变化情况如表3所示。
负荷最大时系统运行如图3所示。

图2 负荷模式一最值时系统运行

负荷1负荷2负荷3电源A电源B电源C电源D支路1-2潮流支路1-3潮流支路2-3潮流初值5060225502850012615966终值501162252228508412613110
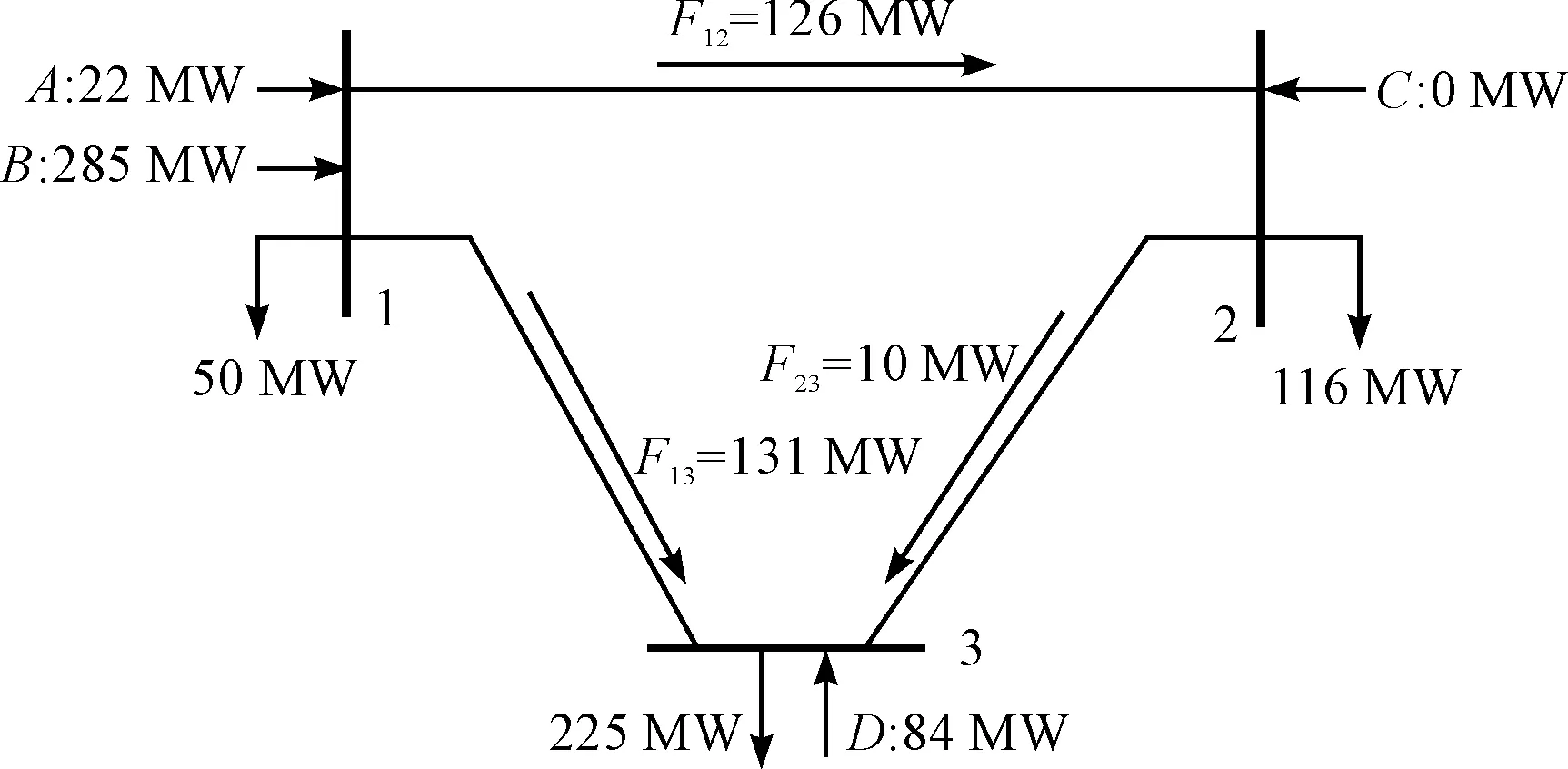
图3 负荷模式二最值时系统运行
此时,随着节点2负荷增大,受网的制约,电源A、支路1-3、支路2-3有功减小,电源D有功增大,支路1-2有功保持不变,网不随电源D同调变化。
2 源网非同调识别指标
与源网非同调相反,同调的源和网指的是源网有功变化同步增大或减小,表现了源网内部无制约和挤兑,可分为一类,显示源的属性;而部分网在源的变化过程中保持不变,相对独立,也可分为一类,显示网的特性;若同调源与其互联的网非同调,则网将其分为独立的类。经过此划分,原电力系统可简化为由同类的源与网组成的简化系统。
同调属性是一个动态变化识别的过程,设当前时刻为t0,定义超前时刻t1时,源网非同调的识别指标为:
(1)


3 蒙特卡洛模拟及源网分类识别
3.1 蒙特卡洛模拟系统运行
在不同时刻电力系统的负荷可能不同,服从随机变化规律,而蒙特卡罗模拟预测法[11]是一种利用随机数来解决具有动态随机性质问题的方法,在电力系统分析中已得到广泛应用[12]。
假设系统的发电、负荷服从区间内的均匀分布,即:
(2)
(3)
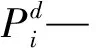

(4)
(5)

3.2 源网同调状态识别
根据潮流计算结果,设t1时刻得到的系统源网功率分别为:
(6)
式中:n—系统节点数;b—支路数。
设t0时刻系统潮流分布已知,表示为:
(7)
则t1时刻相对于t0时刻源和支路的有功变化量分别为:
(8)
其中:
(9)
(10)
根据式(8)的数据,使用(1)的识别指标可识别出系统的同调源和同调网,进一步对式(8)进行计算,可得到识别源网同调的矩阵:
C=(ΔP)T⊗(ΔPl)′
(11)

在上述计算过程中,存在部分源节点保持不变的情况,这部分节点为联络性节点,可根据系统结构将其分类。
4 实验及结果分析
笔者采用IEEE118进行仿真,以验证本研究的算法,系统结构参数参考文献[13]。
经过本研究第1及第2部分分类算法,将系统分为3类的距离比分为两类的小,所以将系统分为3类为最优的分类,分为3类的结果如表4、图4所示。
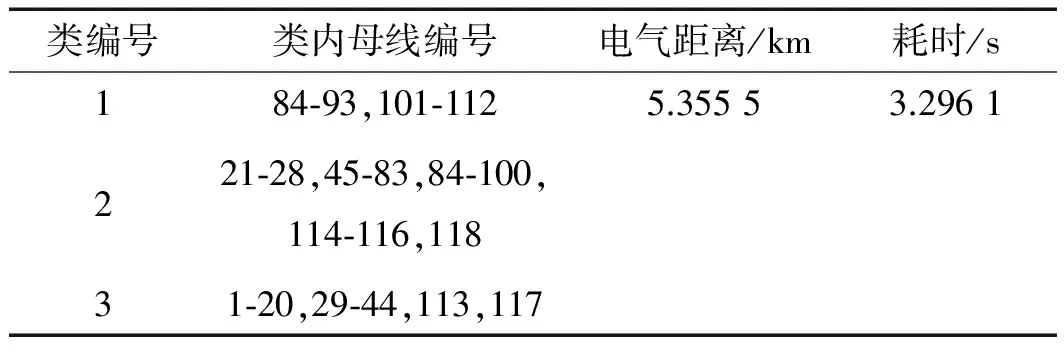
表4 IEEE118母线系统分为3类结果

图4 IEEE118母线系统分为三类示意图
按图4所示的分类结果将系统简化为如图5所示的三母线系统。
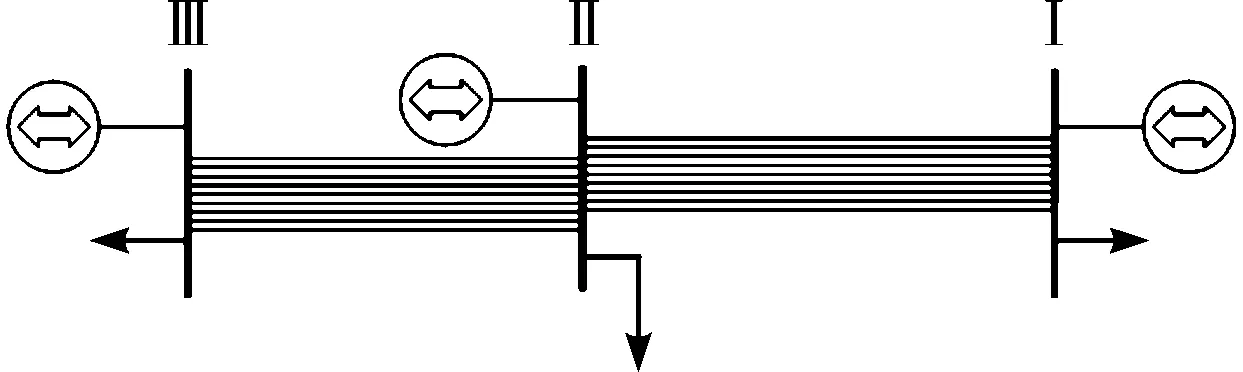
图5 IEEE118母线系统简化为三母线系统示意图
其中,母线Ⅰ与Ⅱ之间有83-84、83-85、94-93、94-92、100-92、100-101、100-103、100-104、100-106共9条并行支路,母线Ⅱ与Ⅲ之间有21-20、23-32、26-30、27-32、28-29、49-42、45-44、65-38、114-31共9条并行支路。
根据文献[14]算法计算图8所示简化电网PTDF矩阵Hr及节点有功注入Pr分别为:
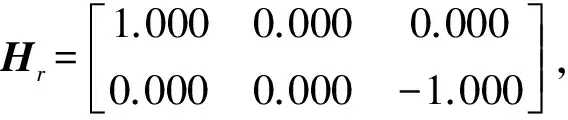
笔者使用本文所提方法对图5所示简化系统进行潮流计算,与文献[14]的比较结果如表5所示。

表5 简化IEEE118母线系统潮流结果比较/MW
5 结束语
本研究根据电网各个电源具有同调的特点提出了一种新的电网简化方法。通过使用本研究所提方法,在算例部分可以看出,可以极大简化电网的分析和调度,有助于提高电网监视的效率,且可以达到与原始电网相同的调度结果。
[1] AAR K B, ALLXLLED S S, MUSTAFA M W, et al. A novel method for ATC computations in a large scale power system[J].IEEETrans.OnPowerSystems,2004,19(2):1150-1158.
[2] OU Y, SINGH C. Assessment of available transfer capability and margins[J].IEEETrans.Onpowersystems,2002,17(2):463-468.
[3] ANNAKKAGE U D, NAIR N K C, LIANG Y, et al. Dynamic system equivalents: a survey of available techniques[J].IEEETransactionsonPowerDelivery,2012,27(1):411-420.
[4] GHASSEMI F, KOO K L. Equivalent network for wind farm harmonic assessments[J].IEEETransactionsonPowerDelivery,2010,25(3):1808-1815.
[5] 刘宝英,杨仁刚.采用辅助问题原理的多分区并行无功优化算法[J].中国电机工程学报,2009,29(7):47-51.
[6] 颜 伟,何 宁.基于Ward等值的分布式潮流计算[J].重庆大学学报:自然科学版,2006,29(11):36-40.
[7] LIANG Min. Total transfer capability computation for multi-area power systems[J].IEEETransactionsonPowerSystems,2006,21(3):1141-1147.
[8] 刘志文,刘明波.基于Ward等值的多区域无功优化分解协调算法[J].电力系统自动化,2010,34(14):63-69.
[9] 苏勋文,米增强,王 毅.风电场常用等值方法的适用性及其改进研究[J].电网技术,2010,34(6):175-180.
[10] XV Jian-zhong, GOLE A M, ZHAO Cheng-yong. The use of averaged-value model of modular multilevel converter in DC grid[J].IEEETransactionsonPowerDelivery,2015,30(2):519-528.
[11] JI Y H, JUNG D Y, KIM J G, et al. A real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions[J].IEEETransactionsonPowerElectronics,2011,26(4):1001-1009.
[12] PATEL H, AGARWAL V. Matlab-based modeling to study the effects of partial shading on PV array characteristics[J].IEEETransactionsEnergyConversion,2008,23(1):302-310.
[13] 王锡凡,肖云鹏,王秀丽.新形势下电力系统供需互动问题研究及分析[J].中国电机工程学报,2014,34(29):5018-5028.
[14] HYUNGSEON O. A new network reduction methodology for power system planning studies[J].IEEETrans.onPowerSystems,2010,25(2):677-684.

