含源支路欧姆定律应用的探究

严明忠

（福建师范大学福清分校电子与信息工程学院，福建福清350301）

含源支路欧姆定律是电学的重要知识点，尤其是在电路分析中应用率较高，因此，注重含源支路欧姆定律的分析，牢固掌握这一重要知识点，有助于提高学生解决电路中各种复杂问题的能力。

一、含源支路及欧姆定律

含有电源的支路称为含源支路。在这类电路中应用欧姆定律较为复杂，尤其是当电路中含有其他电气元件时，需要考虑的问题较多，分析难度较大，容易出现差错。

1.含单电源支路的欧姆定律

如图1一条含源支路，假设电路中的电流由A流向B，电流大小为IA，计算支路中电流、电动势以及电压之间的关系。

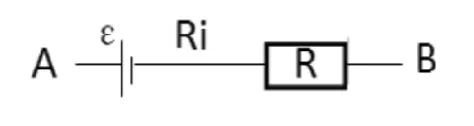
图1

由欧姆定律的微积分理论可得：

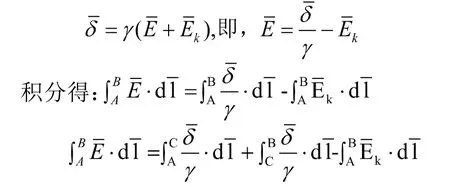
当电源处于放电状态时，电流密度与积分方向并不相同；当电源充电时电流密度和积分方向保持一致。

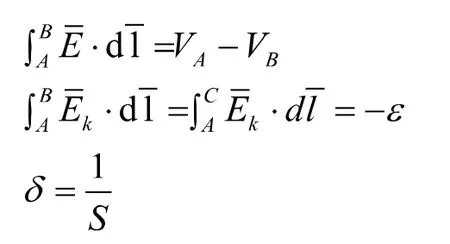
将其带入上式得：

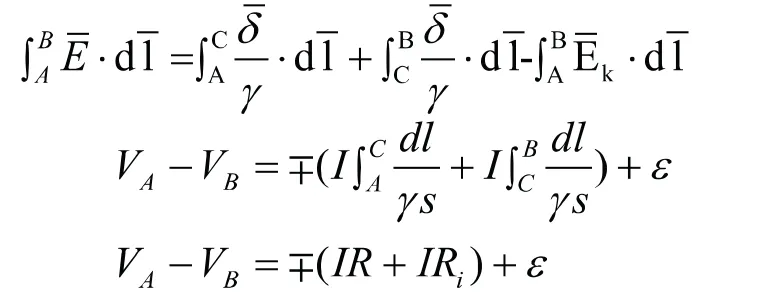
在上述公式中，当电动势和电流方向一致时，取负号；当电动势和电流方向相反时取正号，公式即为含源电路的欧姆定律。其中当电阻R的值为0时，电源处于放电状态，电动势高于端电电源处于充电状态时，电动势低于端电压。当支路电源处于断开状态，支路电流值为0，端电压的值与电动势相同。另外，当A、B两点相连，那么，即电源电动势和电路中总电阻之比即为电路电流。

2.含多电源电路的欧姆定律

在实际的电路中会遇到一条支路中含有多个电源，此时的欧姆定律可用公式表示，其中符号的选择仍是重点。一般按照以下原则确定正负号：任意选取线积分路径方向，将初末两端电势差写出，当积分路径方向和电流方向一致时，电流取负号，反之取正号。另外，当电动势指向和积分路径保持一致时，电动势取正号；当两者反向时取负号。

3.含源支路欧姆定律的拓展

在解决实际电学问题时，常会遇到一些含有复杂节点与支点且无法将其转化为等效并联、串联电路组合的复杂电路，对这类含源复杂电路进行分析时，需在欧姆定律的基础上进行拓展。

图2

如图2的电路由三条含源支路构成，假设回路的绕行方向为顺时针方向，根据知，

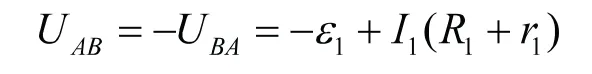
支路AC含有两个电源，可将其等效成一个电源，等效电源的电动势为：方向与电源3的相同，内电阻为两个电源的内电阻之和，即，，由欧姆定律得：

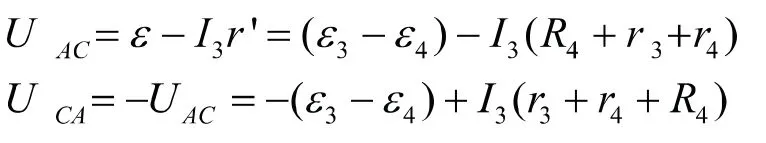
依据回路中电流之间的关系，联合以上公式，得：

选择正负号的依据为：当绕行方向与经过电阻中电流的方向相同，电阻上的电压降为正；当两者的方向相反，则电阻上的电压降为负；当绕行方向和电源电动势方向相同时，电动势的符号为正，当两者的方向相反时，电动势的符号为负。从而得出：任意回路电动势的代数和与电阻上电压的代数和相等，这就是著名的基尔霍夫回路电压方程。

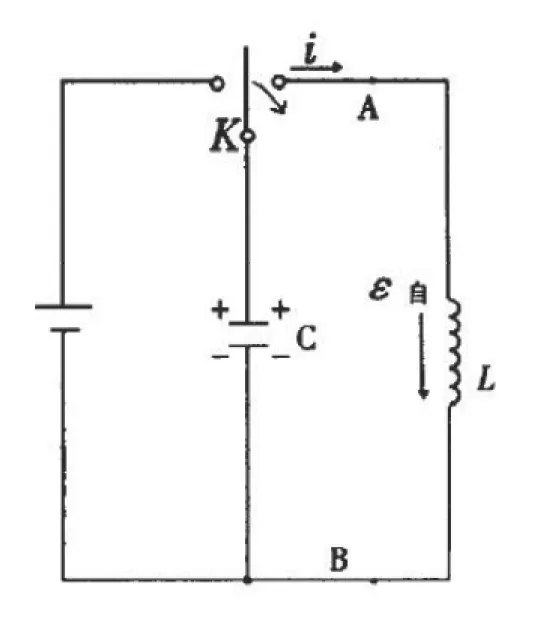
图3

另外，针对一些低频交变电路，直流电路的一些规律仍然适用，可运用含源电路的欧姆定律来解决。

如图3所示，含源电路中存在一LC振荡电路，当开关K向左关闭时，电源会给电容器充电，充电完成后，电容器的上下板分别带上正、负电。当开关向右关闭时，电容器会放电，电流方向如图4所示。受电路中电流变化的影响，线圈会产生自感电动势自，取自感电动势的正方向和电流方向保持一致，那么。振荡回路可看作由两条支路构成，线圈的电阻忽略不计，那么AB右端的支路可看作没有电阻的电源，由欧姆定律知右边支路为对象进行分析与电容器上的电压数值相等，可得电路方程又因电容器处于放电状态可得最终得出电路方程为：

二、含源支路欧姆定律的应用及注意事项

1.含源支路欧姆定律的应用

如图4电路，其中电池A、B的电动势分别为24V、12V，电池A的内电阻为2，电池B的内电阻为1，其中电阻R的值为3。求解：（1）电路中电流大小；（2）电池A、B端U12、U34的值；（3）电池B消耗的化学能功率及输出的有效功率；（4）输入电池B的功率和转为化学能的功率；（5）电阻R的热功率。

图4

（2）假设选择的积分路径从1经电池A到2，使用含源电路欧姆定律可得：

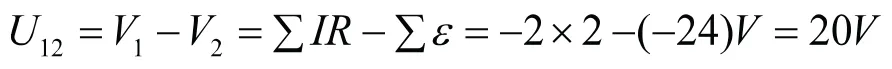
假设积分方向从3流经电池B到4，此时仍可使用含源电路欧姆定律，即：

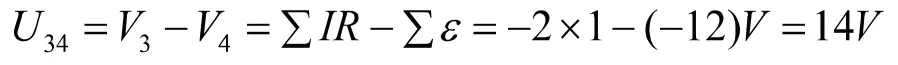
解答第（3）问需借助电动势定义，即，当电源中存在大小为I的电流时，电源做功的功率为：

第（4）问的计算方法和问题（3）相似，可得出输入电池B的功率、转化为化学能的功率、内阻消耗的功率分别为：28、24、4。

需要注意的是依据能量守恒定律，电池A消耗的化学能功率应是两电池内阻上的热功率、消耗在外电阻以及电池B转变成化学能的功率。

2.运用含源支路欧姆定律应注意的事项

在运用欧姆定律解决含源支路相关问题时，为保证分析问题的正确性，应根据电路图实际情况正确判断方向，尤其应牢牢把握以下内容：一般情况下，如电流的方向为正，表明电流实际的方向和假设的方向一致，反之相反。当根据实际状况无法准确判断电流方向时，可先假设电流的方向，依据假设如果得出电流的方向为负，表明电流的真实方向和假设方向刚好相反。但在解题过程中电流的假设方向一旦确定，在进行电路分析时不应再更改假设的电流方向，以确保整个思路的清晰，提高电路图的分析效率。

同时，在解决复杂电路问题时，应注意利用等效法适当简化电路图，看清整个电路的本质，有助于提高电路分析的效率。当然，可能会遇到比较熟悉的电路图，此时应根据经验直接运用之前推导过的公式，也能达到事半功倍的效果。

另外，文中推导出的基尔霍夫回路电压方程在应用过程中有其适用条件，在应用时应注意：当电路中存在n个节点时，可列出的相互独立的节点电流方程数为（n-1）个。同时，新选择的回路至少应有一段电路是已选回路中没有出现过的，而且独立方程个数应和未知数的个数相等。另外，可随意假设每个电路中的电流方向，当得出的结果是负值时，表明假设的电流方向和实际的电流方向相反，反之相同。

总之，含源支路欧姆定律的应用涉及较多知识点，而且部分电路中含有多个电源，甚至含有LC振荡电路，一定程度上增加了电路分析的难度。为此，在对电路进行分析时，应牢记欧姆定律应用过程中应注意的事项，总结含源电路欧姆定律的应用技巧与方法，不断提高电路分析的能力，最终得出正确的电路分析结果。

四、总结

欧姆定律在解决含源电路的相关问题时发挥巨大作用，为此，应充分理解欧姆定律的本质，明确欧姆定律的来龙去脉，尤其要正确选取公式中的正负号。同时，在遇到复杂的电路图时，要在正确理解的基础上灵活运用欧姆定律。

[1]申小海.含源支路欧姆定律应用的探究[J].科技信息(科学教研),2008,(1):211.

[2]周金苟.含源电路欧姆定律及其应用[J].井冈山师范学院学报,2002,(5):56-58.

[3]高祖庆,陶昌,高鹏.含源电路欧姆定律在交直流电路磁路中的拓展[J].曲靖师范学院学报,2006,(3):42-44.

[4]李文静,安工厂.基尔霍夫电压定律在电路分析中的应用[J].电子科技,2013,(7):136-138.

[5]孙武明.用基尔霍夫方程组解复杂电路的讨论[J].许昌师专学报,2000,(2):109-113.

[6]滕建辅,赖崎,张洪暄.节点间含源电路的简化分析法[J].天津大学学报,2003,(5):576-579.

[7]王福谦,张国文,岳丛建.一段含源电路的欧姆定律与库仑场[J].长治学院学报,2005,(5):63-65.

[8]何勇军.电路问题中的等效电源及其运用[J].物理教学探讨,2011,(9):35-36.

[9]颜云华,赵红顺.一段有源支路欧姆定律的教学及推广应用[J].科技创新导报,2008,(18):180.

[10]于新生.由欧姆定律的微分形式导出含源电路的电路方程[J].信阳师范学院学报(自然科学版),1996,(3):256-257.

[11]周亚伯.含源电路欧姆定律教学探讨[J].云南教育,1982,(2):25.

[12]于世新.用电势分析法解一段含源电路和复杂电路[J].物理通报,2013,(3):36-38.