Despeckling of Ultrasound Images Using Modified Local Statistics Mean Variance Filter

Ranu Gupta, Rahul Pachauri and Ashutosh Singh

1 Introduction

In the field of medical imaging various modalities, such as computed tomography (CT),magnetic resonance imaging (MRI), and ultrasound imaging, are used for clinical diagnosis and assessment. Ultrasound is considered one of the most commonly used real time medical imaging techniques. It has got several attractive features like low cost,portable, better image quality, non-invasive i.e. no instrument is placed inside the body,hence, painless. Ultrasound waves consist of frequency range 0.5-30 MHz which lies beyond the human audio spectrum. In medical science, ultrasound brightness mode (B-mode) imaging is the most common modality [Cronan (2006)] in which interested body part is imaged through the ultrasound transducer by placing it on the patient's skin. An ultrasound pulse travels into the body in the form of beam which strikes the tissues with different impedances and gets reflected back as different frequency signals. To convert these signals into a 2-D ultrasound image, signals are processed through the various signal processing units and finally added in constructive/destructive manner. However,resolution of the obtained image is greatly affected by the presence of speckle noise.

Speckle is primarily introduced in the ultrasound image due to interference of the returning signals after scattering process with different frequencies. This scattering process arises due to presence of body organs such as blood cells and blood vessels with different impedances. Speckle in ultrasound B-scans is seen as dark and bright spots and it degrades the quality of the image. Thus, the visualization of a speckled image becomes poor and limits the detectability of diseases by the experts. Speckle noise is also an obstacle to the effective application of image processing and analysis algorithms like segmentation, edge detection, registration etc. Therefore, speckle can be considered as a dominant source of noise in ultrasound images and should be filtered out (despeckled)taking care of important features of the image. Thus, the objective of this work is to present an effective despeckled method for ultrasound images.

In literature, traditional spatial filters have been presented to filter out the speckle noise from ultrasound images. These filters are categorized as: linear (i.e. Wiener, Mean, Lee,Kuan, Frost, etc.) and nonlinear (i.e. median and weighted median etc.). Usually, spatial filters suppress speckle in a better way, but at the same time they have poor edge preserving capability. Therefore, another type of filters, known as local statistics mean variance (LSMV) filters, is mostly preferred in the literature [Christodoulou, Loizou,Pattichiset al. (2002); Kondo, Ichioka, Suzukiet al. (1977); Lee (1981a, b); Lee (1980);Loizou, Pattichis, Christodoulou et al. (2005); Loizou, Pattichis, Christodoulou et al.(2002); Walkup and Choens (1974)] to despeckle the ultrasound images. In this filtering technique, closely resembling regions (i.e. having similar statistics) of an image are replaced by a local mean value, while regions with different characteristics are kept unaltered. The weighted statistics of an image are computed by applying LSMV filter with an optimum odd size window varying from 3×3-15×15. In LSMV filtering, window size significantly affects the quality of despeckled image. A larger size window performs over smoothing and causes loss of subtle details of the image. On the other hand, smaller size window reduces the filtering capability and do not despeckle the image effectively.LSMV filters are non-recursive and do not require any type of transforms which avoids complex 2-D computations. These filters are considered very useful in real time digital image processing applications in the presence of multiplicative as well as additive noise.LSMV filters are easy to implement, process the similar characteristics pixels independently, and exploits the local mean and variance.

The paper is organized further as follows. In section-2, brief literature review of some filters is mentioned. Subsequently in section-3, proposed LSMV filter with its implication is included. Section-4 gives various parameters of analysis. The results and comparative analysis with existing LSMV methods are documented in section-5. Finally, conclusion is presented in section-6.

2 Literature review

Loizou et al. [Loizou, Pattichis, Christodoulou et al. (2005)] evaluated various speckle reduction filters on ultrasound images of the carotid artery. There are various types of spatial filters available in literature. A brief review about them is presented below.

2.1 Mean filter

Mean filter [Gonzalez and Woods (2002); Narayanan and Wahidabanu (2009)] is a simple filter and averages the speckle over the entire image. It blurs the image. It gives unsatisfactory results as the detail information is lost. Therefore mean filter is not the optimal choice.

2.2 Median filter

Median filter [Caloope, Medeiros, Marques et al. (2004); Loupas, Mcdicken, Allen et al.(1989); Pratt (1978)] is used for reducing speckle since it has edge preserving capability.The median filter is implemented by sorting all the values in ascending order and then the median is calculated. It improves the quality of the images as compared to mean filter.The disadvantage is that it is slow and robust and requires large computational time.

2.3 First Order Statistics Filter (Lsmv)

These filters are implemented by calculating first order parameters like mean and variance of the image. All lsmv filters assume that the speckle to be of multiplicative and additive form [Christodoulou, Loizou, Pattichiset al. (2002); Kondo, Ichioka and Suzuki(1977); Lee (1981a, b); Lee (1980); Loizou, Pattichis, Christodoulou et al. (2005);Loizou, Pattichis, Christodoulou et al. (2002); Walkup and Choens (1974)] as given in Eq.(10). The types of lsmv filters are summarized below.

2.3.1 Lee filter

Lee filter [Lee (1981a, b); Lee (1980)] is based on multiplicative noise as well as additive noise. It can effectively preserve the edges and important features. Lee filter is based on minimizing the mean square error (MMSE). It applies linear approximation and local mean and variance is calculated. If the variance over the window is low, smoothing will be done. Lee filter is described as:

where,

and σχ2is the variance of the pixel values within the kernel and defined as:

where MxM is the size of the mask window and gn,mis the pixel value within the window at indices n and m, g̅ is the mean value within the window. The parameter σ2is the variance of the whole image. The disadvantage of Lee filter is that it ignores noise closer to the edges in the image.

2.3.2 Wiener filter

The Wiener filter [Kondo, Ichioka and Suzuki (1977); Walkup and Choens (1974)] is a linear filter in spatial domain. Wiener filter can be used in frequency domain as well as in spatial domain. The frequency domain Wiener filter is used for both denoising and deblurring, while spatial domain is used for denoising only. The statistical properties in an image vary from one region to other. The global statistics (like mean, variance) and local statistics are important. Wiener filter is based on both, global and local statistics and is given by:

where f(n,m)is the approximated noise-free pixel, g(n,m)is the noisy pixel, g̅ is the localmean value within the window and, k(n,m)is a weighting factor and n, m are the pixel coordinates. The factor k(n,m)in a moving window is given by:

The values σ2and σn2are the variance in the moving window and in the whole image.The noise variance is calculated by computing the average within a window which is larger than the filtering window. The noise variance is calculated as:

To some extent it preserves the edges and other detailed information. The disadvantage of this method is the higher time consumption.

2.3.3 Other lsmv filter

It can be found in the literature [Loizou, Pattichis, Christodoulou et al. (2005)] that by varying the weighting factor kn,mdifferent local statistics mean variance (lsmv) filters can be formed. These weighting factors may be derived as:

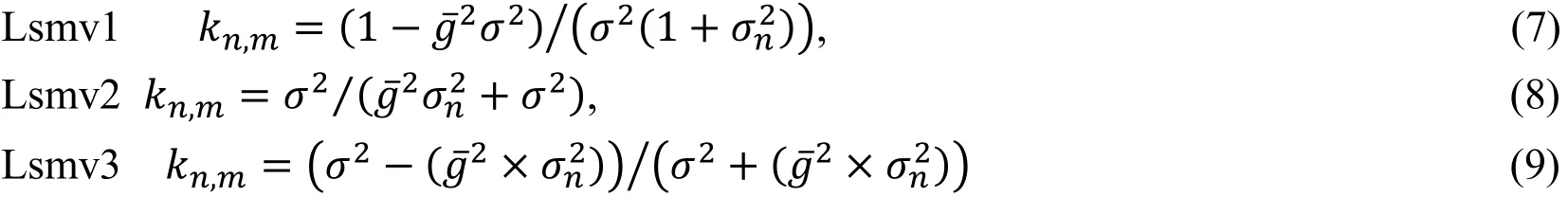
Despite remarkable advancement in image quality over the past decade, small progress has been made towards removing the speckle from ultrasound B-scan mode images.Whether speckle is viewed as image signal or noise depends largely on the imaging context. Some researchers believed that the despeckle filters as mentioned in Eq. (10)-(12)reduces speckle but at low variance but for the higher level of noise variance the quality of the image is degraded drastically. Thus the aim of this article is to design an lsmv filter which maintains the quality of the image at higher noise variance level and at the same time it would remove the noise from the image.

3 Proposed method

In order to propose an efficient despeckling filter, suitable speckle noise model should be established. It is well evident in the literature [Frost et al. (1982)] that an ultrasound image contains additive as well as multiplicative noise. Therefore, envelope of a noisy image can be expressed as:

where, zi,jdenotes the noisy pixel,xi,jdenotes the noise free pixel, ni,jand ai,jdenotes the multiplicative and additive noise respectively, and i,jare the real numbers representing the indices of the pixel locations in 2-D image. Since, the effect of additive noise is considerably less significant [Michailovich and Tannenbaum (2006)] in comparison to multiplicative noise, thus Eq. (10) can be approximated as:

The logarithmic compression transforms the multiplicative noise into additive noise which enables it into an additive white Gaussian noise model. The speckle noise after logarithmic compression becomes very close to the uncompressed signal having Rayleigh distribution. Thus, after applying logarithmic compression Eq. (11) becomes:

For the rest of the article, the term lg(zi,j) which is the observed pixel after logarithmic compression is denoted as gi,j, and the terms lg(xi,j), and lg(ni,j) are the noise-free pixel and noisy component termed as fi,jand nli,jrespectively.

It has been described in the literature that most of the methods use local statistics for speckle reduction filtering and in all of them it is assumed that the speckle noise model has a multiplicative form as mentioned in Eq. (10). The filters using local statistics such as mean and variance of the neighborhood can be described with model illustrated as in Eq. (13). Therefore, filtering algorithm for this model has been expressed with the following equation [Loupas, Mcdicken and Allen (1989)]:

where fi,jis the noise free pixel, g̅ is the local mean value, gi,jthe noisy pixel and i,j are the pixel coordinates,ki,jis the weighting factor with k ∈ (0….1) expressed as:

where σ2is the local variance of the moving window of size 5×5. The local statistical parameters are more important rather than global parameters in the image. Thus, the proposed method has given more emphasison the local statistical parameters. If the centre pixel is on the edge the weighting factor would approach to one and the pixel remains unchanged whilefor other than the edge, the weighting factor would be high or low depending upon the amount of noise. Better smoothing takes place for larger noise variance. In this work, filtering has been carried out after contaminatingoriginal image with synthetic speckle noise of different variance.

From the simulation results and their analysis following conclusions have been drawn:

(i) If gi,j＜ g̅ and σ2≫ then gi,jis the position of pixel where image intensity does not change and local variance is high. In this case, smoothing takes place and weighting factor ki,jreaches closer to one or zero depending upon the noise. It helps to recover the fine details of the image.

(ii) If gi,j＜ g̅ and σ2≪ then gi,jis the position of pixel where image intensity does not change and local variance is low. In such position the weighting factor ki,jrapidly reaches closer to one and more smoothing will be done.

(iii) If gi,j＞ g̅ and σ2≫ then gi,jis the position of pixel where image intensity changes very rapidly indicating the edge pixel and local variance is high. In such position the weighting factor ki,jrapidly reaches closer to zero and less smoothing will be done in order to preserve the edges.

(iv) If gi,j＞ g̅ and σ2≪ then gi,jis the position of pixel where image intensity changes very rapidly indicating the edge pixel and local variance is low. In such position the weighting factor ki,jrapidly reaches closer to zero and less smoothing will be done in order to preserve the edges.

The mean and standard deviation of original ultrasound image of carotid artery as well as for despeckled image by various methods is calculated for lumen, tissue and adventia layer. The higher mean values of proposed filter in Tab. 1 indicates brighter image and low values of standard deviation in comparisons to other filters indicates that the proposed method preserves the edges efficiently.

Table 1: Mean and Standard deviation of different filters with the proposed

4 Performance Indices

In this study, ultrasound images of the carotid artery were taken for the investigation.Total of six filters, including proposed filter, were applied for the despeckling of the images. The performance of these filters was investigated on the basis of following indices:

4.1 Universal Quality Index (Q)

Universal quality index is a combination of three different performance parameters: loss of correlation, luminance distortion, and contrast distortion. Mathematically it is defined as [Wangand Bovik (2002)]:

where g̅ and f̅ represent the mean of the original and despeckled image, σgand σfrepresent the standard deviation of original and despeckled image of the analysis window,σgfrepresent the covariance between the original and despeckled image. Q is computed for a sliding window of 88 size. If gi,j=fi,jthen it is 1 and if fi,j=2g̅-gi,jthen it is-1 which is the lowest.

4.2 Structural similarity index Measure (SSIM)

The structural similarity index between two images is given by Wanget al.[Wang, Bovik,Sheikh et al. (2004)]:

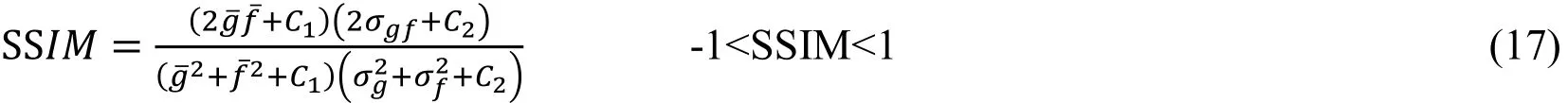
where C1=0.01dr andC2=0.03dr with dr=255 is the dynamic range for the gray scale ultrasound image. The range of SSIM lies between -1 to +1. -1 is for a bad and +1 is for a good similarity. It is calculated similar to Q for 8x8 window size.

4.3 Geometric Average Error (GAE)

The geometric average error (GAE) is computed as [Winkler (2000)]:

If there is a small difference between the original and the despeckled image then geometric average error is approaching towards zero otherwise it is high.

4.4 Mean Square Error (MSE)

It measures the change in quality between the original and processed image.

If the difference between the original image and despeckled image is low then MSE is low for a better despeckled image.

4.5 Peak Signal to Noise Ratio (PSNR)

It is defined as:

where Imaχis the maximum intensity of the pixel in the noisy image. PSNR is higher for a better filtered image and lower for a poorly filtered image.

5 Results and Discussion

The proposed method is analyzed on the parameters like MSE, PSNR, GAE, Q, and MSSIM. The performance analysis is done for noise variance of the range from 0.01 to 0.09 with zero mean. The parameter analysis is done on longitudinal B-mode carotid artery ultrasound image taken from AlokaProsound Ultra-6 of frequency 7.5 MHz.The proposed method has been implemented on MATLAB7.9.0 (R2009b) software background.The parameter analysis is done on Intel(R) Core (™) 2 Duo CPU T5870@2.00 GHz with 3GB RAM computer. The results obtained for different noise variance is listed in Tab. 2.

Table 2: Results of different parameters with different speckle noise variance of Proposed Method (0.01-0.09)

From Tab. 2, it is quite clear that in the proposed method mean square error is quite low.The geometric average error is zero which shows that the proposed filtering approach is good. The quality index and mean structural similarity index is approaching towards one which shows that the quality of the image is better.

5.1 Comparative analysis

A comparison has been made on 20 ultrasound carotid artery images between proposed and existing methods based on performance indices shown in section-3. For this comparison, the original ultrasound image taken is shown below. The speckle is introduced synthetically through Mat lab. After despeckling by using various filter methods the output image is also shown below.

Figure1: Despeckled images with various filters at σ2=0.06 (a) original image (b)speckled image, despeckled images by (c) lsmv1, (d) lsmv2, (e) lsmv3, (f) proposed, (g)Wiener, (h) Lee filters

By visualization from Fig. 1, that the picture quality of Lee filtering is very poor as compared to other filters. Further, this is quantified and verified by evaluating all the performance parameters. Although lsmv1 and lsmv3 are performing better than Lee filter but are still inferior to Wiener, lsmv2 and proposed filter. But it is quite difficult to visualize and quantify the difference in the performances of lsmv2, Wiener and proposed filtering methods from Fig. 1. Therefore, their performance comparison is done on the basis of performance indices stated above and the results obtained are shown in Tab. 3 and Fig. 2.

Table 3: Comparisons of various filters with the proposed method at 0.06 noise variance level

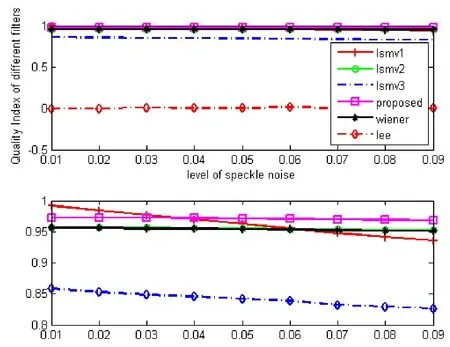
Figure 2(a): Comparison of quality index for different filters

Figure 2(b): Comparison of MSSIM for different filters

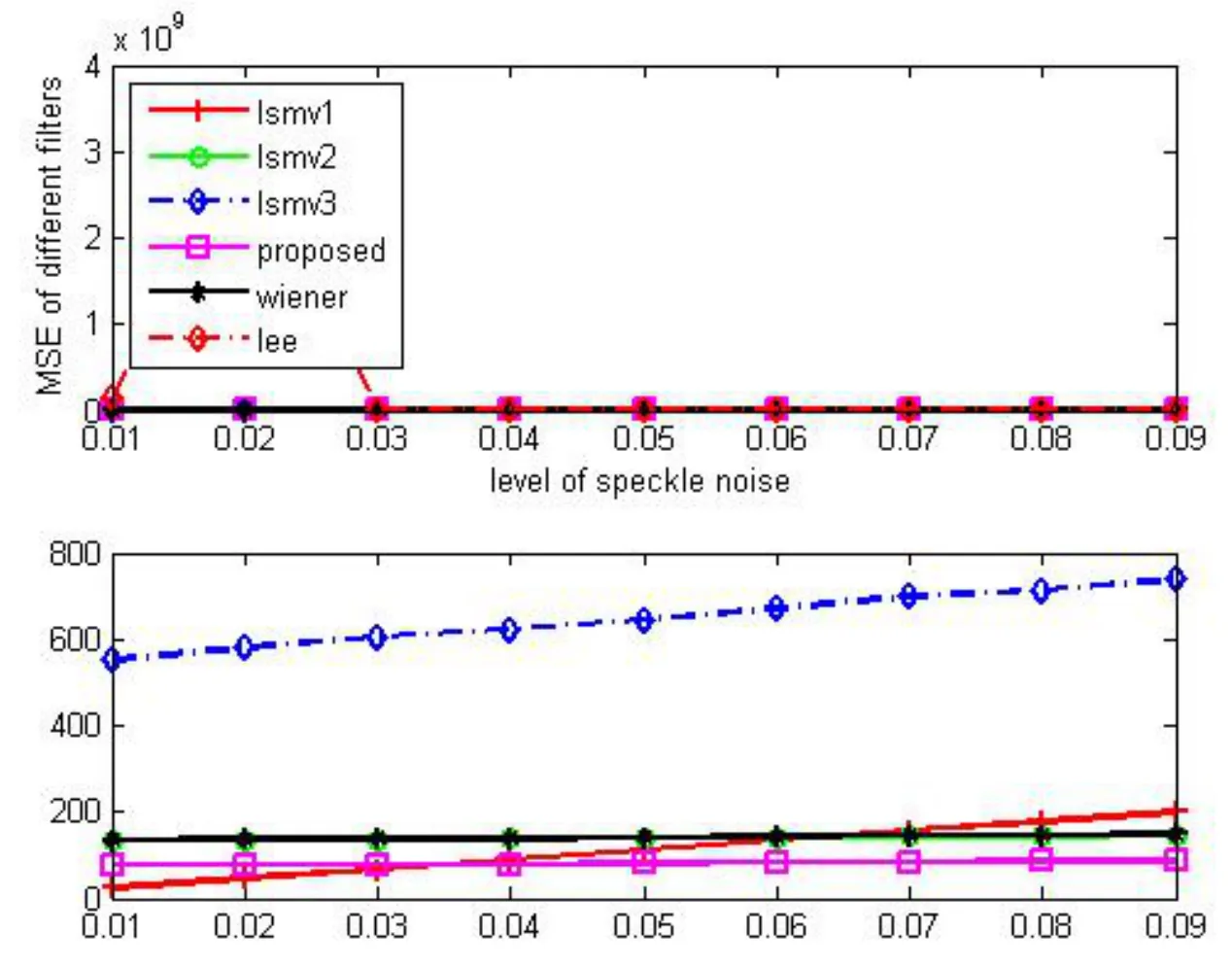
Figure 2(c): Comparison of MSE for different filters

Figure 2(d): Comparison of PSNR for different filters

As evident from the comparison of Universal Quality Index shown in Fig. 2(a), that the higher value of quality index even for higher noise variance from the proposed method preserves the information of the image in a better way as compared to the other methods. The higher value of MSSIM for the proposed method as it is evident from Fig. 2(b) shows that the proposed method preserves the edges in a superior manner which is important for intimamedia thickness measurement. Since the mean square error is less as shown in Fig. 2(c),therefore its peak signal to noise ratio is high as depicted from Fig. 2(d).

6 Conclusions

Speckle noise removing is a prior step for further processing of image. It detoriates the quality and visualization of the image. Thus making it difficult for the doctors to diagnose the disease of the patient for future treatment. Thus a better speckle reduction as the proposed method would definitely solve the problem. In this paper a local statistics mean variance filter method is proposed and its performance analysis is done on almost 20 data sets on various parameters as mentioned above. The comparison is done only for one iteration and the size of window is 5×5. The comparison results show that the proposed method is superior method than existing ones. It removes the speckles in a better way and at the same time preserves the edges. The experimental results show that local mean and variance technique is very effective tool in noise filtering applications.

Disclosure: The authors state no conflict of interest and have nothing to disclose. The research was not supported by any financial help.

Caloope, P. B.; Medeiros, F. N. S.; Marques, R. C. P.; Costa, R. C. S. (2004): A comparison of filters for ultrasound images. International Conference on Telecommunications,pp. 1035-1040.

Christodoulou, C. I.; Loizou, C. P.; Pattichis, C. S.; Nicolaides, A. (2002): Despeckle filtering in ultrasound imaging of the carotid artery. The Second Joint meeting of the IEEE Engineering in Medicine and Biology society and the Biomedical Engineering Society (EMBS/BMES) Houston, Texas, pp. 1027-1028.

Cronan, J. J. (2006): Ultrasound: is there a future in diagnostic imaging? Journal of the American College of Radiology, vol. 3, no. 9, pp. 645-646.

Frost, V. S.; Stiles, J. A.; Shanmugan, K. S.; Holtzman, K. C. (1982): A model for radar images and its application for adaptive digital filtering of multiplicative noise. IEEE Transaction on Pattern Analysis and Machine Intelligence, vol.4, no. 2, pp. 157-165.

Gonzalez, R. C.; Woods, R. E. (2002): Digital Image Processing. Addison-Wesley Publishing Company.

Kondo, K.; Ichioka, Y.; Suzuki, T. (1977): Image restoration by Wiener filtering in the presence of signal dependent noise. Applied Optics, vol. 16, no. 9, pp. 2554-2558.

Lee, J. S. (1981): Speckle analysis and smoothing of synthetic aperture radar images.Computer Graphics and Image Processing, vol. 17, no. 1, pp. 24-32.

Lee, J. S. (1981): Refined filtering of image noise using local statistics. Computer Graphics and Image Processing, vol. 15, no. 4, pp. 380-389.

Lee, J. S. (1980): Digital image enhancement and noise filtering by using local statistics.IEEE Transaction on Pattern Analysis and Machine Intelligence, vol. 2, no. 2, pp. 165-168.

Loizou, C. P.; Pattichis, C. S.; Christodoulou, C. I.; Istepanian, R. S. H.; Pantziaris,M. et al. (2005): Comparative evaluation of despeckle filtering in ultrasound imaging of the carotid artery. IEEE Transactions on Ultrasonic, Ferroelectrics and Frequency Control, vol. 52, no. 10, pp. 1653-1669.

Loizou, C.; Christodoulou, C.; Pattichis, C. S.; Istepanian, R.; Pantziaris, M. et al.(2002): Speckle reduction in ultrasound images of atherosclerotic carotid plaque. IEEE 14thInternational Conference on Digital Signal Processing Santorini, Greece, July 1-3,pp. 525-528.

Loupas, T.; Mcdicken, W. N.; Allen, P. L. (1989): An adoptive weighted median filter speckle suppression in medical ultrasound images. IEEE Transaction on Circuits Systems,vol. 36, pp. 129-135.

Michailovich, O. V.; Tannenbaum, A. (2006): Despeckling of medical ultrasound images. IEEE Transaction on Ultrasonic Ferroelectrics and Frequency Control, vol. 1,no. 53, pp. 64-78.

Narayanan, S. K.; Wahidabanu, R. S. D. (2009): A View on despeckling in ultrasound imaging. International Journal of Signal Processing, Image Processing and Pattern Recognition, vol. 2, no. 3, pp. 85-98.

Pratt, W. K. (1978): Digital Image Processing. Wiley, New York.

Walkup, J. F.; Choens, R. C. (1974): Image processing in signal dependent noise.Optical Engineering, vol. 13, no. 3, pp. 250-266.

Wang, Z.; Bovik, A. C.; Sheikh, H. R.; Simoncelli, E. P. (2004): Image quality assessment: From error measurement to structural similarity. IEEE Transaction on Image Processing, vol. 13, no. 4, pp. 600-612.

Wang, Z.; Bovik, A. (2002): A universal quality index. IEEE Signal Processing Letters,vol. 9, no. 3, pp. 81-84.

Winkler, S. (2000): Vision models and quality metrics for image processing applications(Ph.D. Dissertation). University of Lausanne, Switzerland.