Complex Modal Analysis for the Time-Variant Dynamical Problem of Rotating Pipe Conveying Fluid

Lihua Wang and Zheng Zhong

1 Introduction

Time-variant dynamical systems are widely used in many aerospace and mechanical engineering applications, such as deployable spacecraft antenna, belt-pulley drives, water supply and sewerage, and petroleum transmission. Pipe conveying fluid system is a typical time-variant system in which vibration characteristics and dynamic stability are of critical importance. For conventional time-dependent problems, finite difference method(FDM) is a typical method to deal with the time-domain discretization [Mitchell and Griffiths (1980); Weiland (1996)]. However, FDM tends to be unstable if the critical time step is not properly selected. Restrictions to regular problem domain and slow rate of convergence also hinder the development of FDM. Finite element method (FEM) became popular after 1940s because of its easy implementation in complex geometry and desirable stability [Matagne, Leburton, Destine et al. (2000); Shi, Yang, He et al.(2013); Shi and Lan (1999)]. Although FEM is first introduced to discretize the space domain, it's also a good candidate for the discretization in the time domain, which is called time-domain finite element method [Lee, Lee and Cangellaris (1997); Xu and Prozzi (2015)]. For time-variant problems, although the solutions based on time-domain FEM are continuous in time domain, the continuity of their derivatives can not be guaranteed. However, this is vital to the accuracy and convergence of time-variant problems. Besides, the difficulty of unstructured 3-D mesh generation is also an obstacle to its wide use.

Considering the study techniques on time-variant pipe conveying fluid model, Guran et al.[Guran and Atanackovic (1998)] presented an analytical solution for the model with shear and compressibility and Thomsen et al. [Thomsen and Dahl (2010)] gave an analytical prediction for its primary resonant response. Some other researchers such as Sugiyama et al. Sugiyama et al. [Sugiyama, Katayama and Kanki (1996)] and Paidoussis et al.[Paidoussis and Semler (1998)] made many efforts on the experimental studies to validate the theoretical investigations. Numerical simulations were proposed by using Galerkin method [Thomsen and Dahl (2010); Huo and Wang (2016); Chellapilla and Simha (2007);Yan, He, Zhang et al. (2009)], hybrid Galerkin-Fourier method [Paidoussis (2008)]multiple scales method [Sorokin and Terentiev (2003)], power series method [Fung and Yan (1999)], variational iteration method [Li and Yang (2017)], Newmark method[Wang (1998)] etc. For the rotating flexible pipe conveying fluid model, the solution techniques include Galerkin method [Panussis and Dimarogonas (2000)], Runge-Kutta method [Yoon and Son (2007); Wang and Zhong (2014)] and some meshfree methods such as radial basis collocation method [Wang and Zhong (2015)]. Although many numerical methods can be used for solving such problems, very few analytical or semi-analytical solutions can be found for reference of different models.

For time-variant problems, the damping is time-variant and usually non-classical[Veletsos and Ventura (1986)], and the natural frequencies and modes of vibration are complex. Therefore, the standard mode superposition method is no longer applicable to the time-variant dynamic analysis, and the equations of motion have to be decoupled in the complex domain in which the technique of complex modal analysis was developed[Lee (1991); Kraver, Fan and Shah (1996)]. Kessler [Kessler (1999)] introduced complex modal analysis for the rotating systems and presented the two sub-modes of forward mode and backward mode. The complex mode superposition method was performed by Oliveto et al. [Oliveto, Santini and Tripodi (1997)] for the dynamical analysis of a simply supported beam with two rotational viscous dampers attached at its end. Agostini et al.[Agostini and Souza (2010)] presented a complex modal analysis in conjunction with finite element method for the vibration analysis of vertical rotors with gravitational and gyroscopic effects. Complex modal analysis method has been frequently used for solving time-invariant linear equations of motion. However, time-variant complex modal analysis is still lack of investigation.

In this paper, we present a complex modal analysis for the time-variant rotating pipe conveying fluid system. A semi-analytical procedure for the investigation of complex frequencies and modes of vibration is proposed and the orthogonality conditions which allow the decoupling of the equation of motion are derived. Exact responses of damped linear vibrating systems to arbitrary excitations are obtained. Numerical examples are studied to validate the proposed method.

2 Discretization for the dynamical problem of rotating pipe conveying fluid

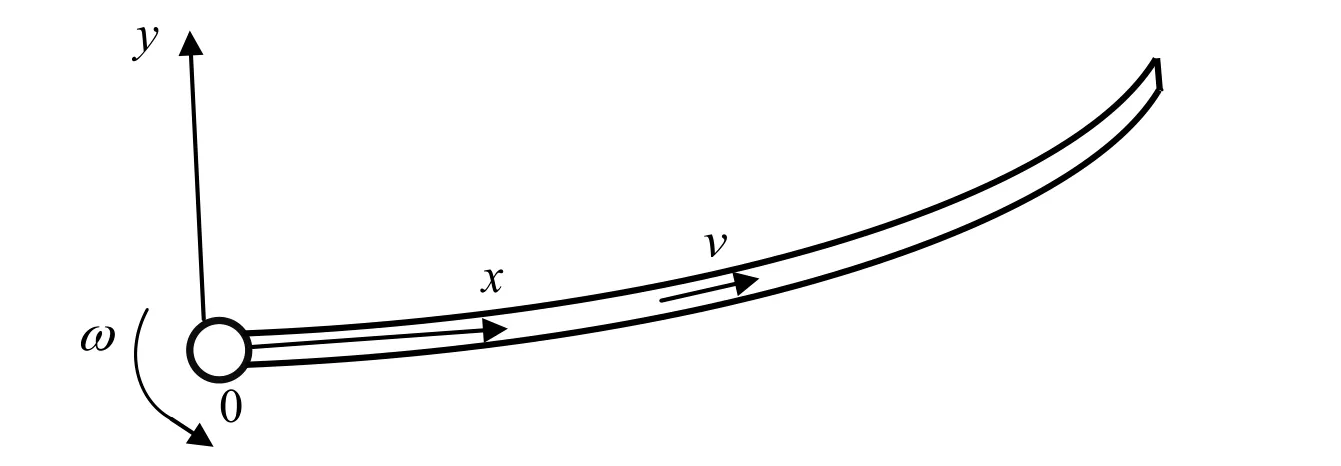
Figure 1: Schematic model of a rotating flexible pipe conveying fluid

Consider a rotating flexible pipe conveying fluid and its schematic model is shown in Fig.1. Atx = 0, the end is fixed and the system is subjected to fixed-axis rotation. Atx = L whereL is the length of the pipe, the end is free. The governing equation of motion for this system which has been derived in Wang et al. [Wang and Zhong 2014)] is given as

where u is the transverse displacement,M1is the mass per unit length of the pipe,M2is the mass per unit length of the fluid,ω0is the angular velocity of the pipe rotation,v =v(t)is the velocity of the fluid and t is the time,EIis the bending stiffness of the pipe.

By utilizing the classical separation of variables technique [Wang, Hu, Zhong et al.(2009)], the solution of Eq. (1) can be expressed as

wheren is the number of discretized terms, and dj(t)are the non-dimensional temporal functions in generalized coordinates. For the cantilever boundary conditions considered in this system,φj(x)can be expressed as

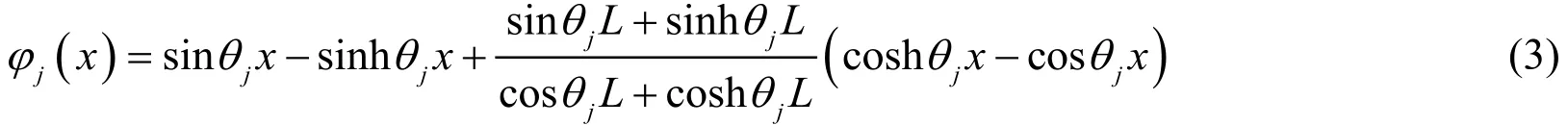
where θjcan be obtained from the equation cosθjL c oshθjL =-1. Substituting (2) into the governing equation of motion (1), multiplying it byφi( x), and integrating the equation from x=0to L, subsequently, the discretized equation of motion for the system can be formulated as

with

in which i,j = 1 ,2,… ,nandδijis the Kronecker delta function. The initial conditions for Eq. (4) are given as

3 Complex modal analysis

Consider a general dynamical problem with time-variant coefficients of the following form

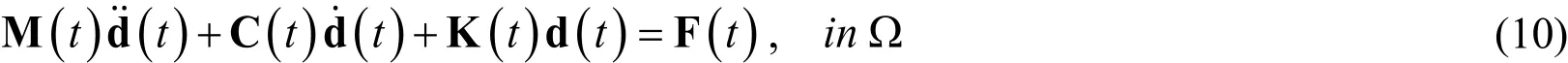
where M (t)is the mass matrix,C (t)is the damping matrix and K(t)is the stiffness matrix.F (t)is the arbitrary excitation matrix, and Ωis the problem domain. In the proposed problem, Eq. (4) can be taken as a special case of Eq. (10) and hereinM is a constant matrix. WhenM(t)is a non-singular matrix, Eq. (10) can be reformulated as

After that, we define an unknown vector as

Combining (11) and (12) we can obtain

where

and I is an identity matrix. The initial conditions are given as

Combining (12) and (15) we can gain the combined initial conditions as

Invoking the initial conditions in Eq. (16), the general solution of Eq. (13) can be expressed as

where

Defining ξas the roots of the following eigenfunction, we have

in which the eigenvectors corresponding to eigenvalues ξiare yi, i.e.

and yisatisfy the following condition

Next, define a generalized mode matrix as

Combining Eq. (20) and Eq. (22) we have

Since the eigenvalues are diverse, the eigenvectors are linear independent. Therefore, we

can multiply Y-1(the inverse matrix of Y ) on both sides of Eq. (23) which renders

Eq. (24) can be rewritten as

Subsequently we can obtain

Finally, substituting (26) into (17) gives the general solution of Eq. (10) as

4 Comparison of finite difference method and complex modal analysis

In finite difference method, we take Runge-Kutta method as an example. In Runge-Kutta method, Eq. (10) can also be reformulated as in Eq. (13). Evaluate one arbitrary row in Eq. (13), which can be expressed as

Fourth-order Runge-Kutta method is employed as follows

where

The requirement of stability gives the amplification factor as

and we can obtain the stability condition as follow

This describes that Runge-Kutta method is conditionally stable. The convergence of Runge-Kutta method has the fourth-order accuracy as

Follow the same procedure, we can also find the stability condition and accuracy for any other finite difference methods.

In complex modal analysis, since no discretization is implemented in the time domain,this method is always unconditionally stable. The convergence of complex modal analysis only depends on the method utilized for numerical integration. For example,when using n -th order Gauss integration, this proposed scheme has the accuracy as

5 Numerical examples

The material coefficients of the rotating pipe conveying fluid model are: elastic modulus of the pipe E = 7 .8×109Pa, cross-sectional area of the pipe A = 1 .57 × 10-8m2,moment of inertia of the pipeI = 1 .21×10-17m4, length of the pipe L =0.025m, mass per unit length of the pipe= 1 .884×10-5kgm, mass per unit length of the fluid= 1 .6485×10-5kgm. The coefficients of initial conditions are=0.001m,u˙0=0ms. Denote a as a positive integer in the numerical simulations.v＞0defines the fluid flows from the fixed end to the free tip and v＜0defines the fluid flows from the free tip to the fixed end. Since damping is involved in Eq. (10), the eigenvalues corresponding to the system are complex. We define the eigenvalue asξ=σ+ωi, in which the real part of the eigenvalueσdescribes the damping of the system and the imaginary partωsignifies the frequencies of the system.

Figure 2: Numerical solution for the tip displacement of the pipe whenv =a,ω0=100rads

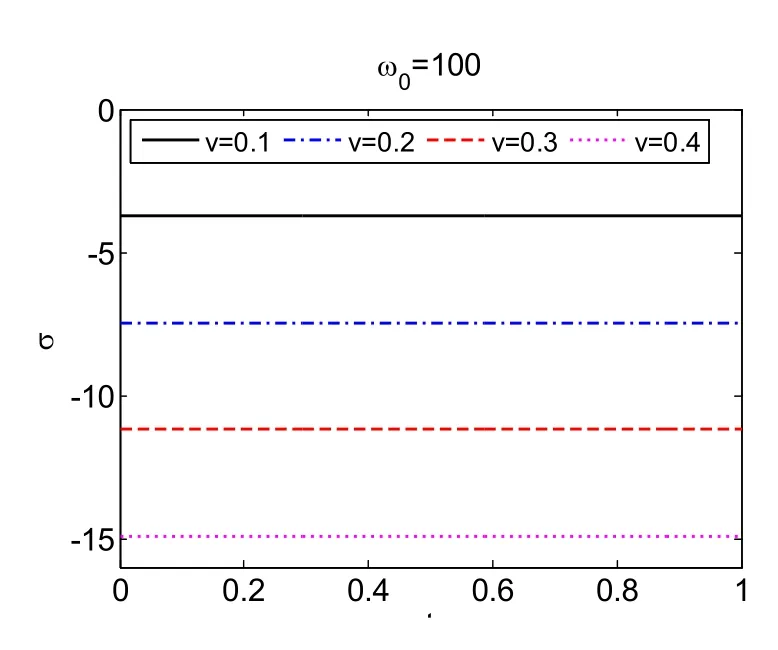
Figure 3: Damping of the system when v =a,ω0=100rads

Figure 4: Fundamental Frequency of the system when v =a,ω0=100rads

Figure 5: Numerical solution for the tip displacement of the pipe when v = at,ω0=100rads

Figure 6: Damping of the system when v =at,ω0=100rads

Figure 7: Fundamental Frequency of the system when v =at,ω0=100rads

Figure 8: Numerical solution for the tip displacement of the pipe when v = at2,ω0=100rads

Figure 9: Damping of the system when v = at,ω0=100rads

Figure 10: Fundamental Frequency of the system when v =at2,ω=100rads0

Table 1: Comparisons of CPU time cost in Runge-Kutta method and complex modal analysis when v＞0,ω0=100rads

Runge-Kutta 2753.98 2828.39 2903.04 2975.84 CMA 13.84 13.88 13.87 13.88

Figure 11: Numerical solution for the tip displacement of the pipe when v = -a,ω0=100rads

Figure 13: Fundamental Frequency of the system when v =-a,ω0=100rads

Figure 16: Fundamental Frequency of the system when v = -at,ω0=100rads

Table 2: Comparisons of CPU time cost in Runge-Kutta method and complex modal analysis when v＜0,ω0=100rads

Figure 17: Numerical solution for the tip displacement of the pipe under different angular velocities when v =0.2ms

Figure 18: Damping of the system under different angular velocities when v =0.2ms

Figure 19: Fundamental Frequency of the system under different angular velocities when v =0.2ms

Figure 20: Numerical solution for the tip displacement of the pipe under different angular velocities w hen v =0.2tms

Figure 21: Damping of the system under different a ngular v elocities w hen v =0.2tms

Figure 22: Fundamental Frequency of the system under different angular velocities when v =0.2tms

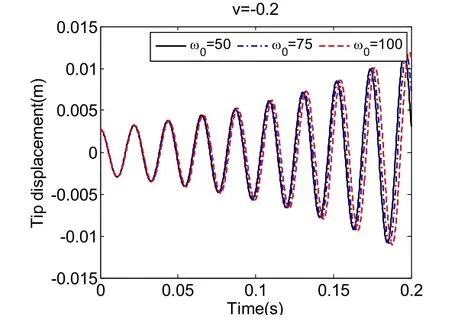
Figure 23: Numerical solution for the tip displacement of the pipe under different angular velocities when v = -0.2ms

Figure 24: Damping of the system under different angular velocities when v =-0.2ms

Figure 25: Fundamental Frequency of the system under different angular velocities when v =-0.2ms

Figure 26: Numerical solution for the tip displacement of the pipe under different angular velocities when v =-0.2tms

Figure 27: Damping of the system under different a ngular velocities w hen v =-0.2tms.

Figure 28: Fundamental Frequency of the system under different angular velocities when v =-0.2tms

We fist compare the numerical solutions obtained from Runge-Kutta method and complex modal analysis. As shown in Fig. 2, Fig. 5, Fig. 8, Fig. 11 and Fig. 14, the solutions obtained from the two methods are in good agreement with each other.Complex modal analysis is much more efficient than Runge-Kutta method when comparing the computation time in the solutions as schematized in Tab. 1 and Tab. 2,which describe that the CPU time cost in complex modal analysis is two orders of magnitude lower than time cost in Runge-Kutta method. Furthermore, solution of complex modal analysis is always stable and its accuracy only depends on the accuracy of numerical integration. Solution of Runge-Kutta method is conditionally stable and the solution becomes unstable if the critical time step cannot satisfy the stability conditions in(32). Generally, in order to guarantee the stability condition, very small time step is required which leads to a lot of computation costs.

We then investigate the influences from the velocity of the fluid v. The angular velocity of the pipe rotation is set to be a constantω0=100rads. When vis a constant and positive, Fig. 2 illustrates that tip displacement of the pipe is gradually decreasing. Higher vmakes the tip displacement decreases faster. Similar phenomenon can be observed in Fig. 5 whenv is a linear function and in Fig. 8 when vis a quadratic function.Damping of the system is presented in Fig. 3, Fig. 6 and Fig. 9 which demonstrate that the damping of the system is a constant whenvis a constant, the damping is growing linearly whenv is a linear function and it's growing quadratically when vis a quadratic function. The fundamental frequencies are displayed in Fig. 4, Fig. 7 and Fig.10. The frequencies are constants whenv is a constant. Higher vintroduces lower frequency of the system. The frequencies of the system are decreasing whenvis increasing with time. The fastervincreases, the faster the frequency decreases.

As shown in Fig. 11 and Fig. 14, when the velocity of the fluidv＜0, the resulting amplitude of the pipe is growing with time. The higher the velocity is, the faster the amplitude increases. Whenvis a constant and negative, the negative damping [Wang,Hu, Zhong et al. (2009, 2010)] of the system is a constant as shown in Fig. 12, and when vis a linear function and negative, the negative damping of the system increases linearly as exhibited in Fig. 15. The variations of frequency displayed in Fig. 13 and Fig.16 are the same as in the cases ofv＞0.

To compare the influences of pipe angular velocity on the response of the system vibration, we set the velocity of fluidvas a constant as shown in Fig. 17 and Fig. 23.Different angular velocities lead to little change of the system frequency since the angular velocity does not affect the stiffness term in (7) very much. Angular velocity hardly affects the pipe amplitude. Higher angular velocity brings in lower frequency of the system regardless of whethervis positive or negative, which can be checked in Fig. 19 and Fig. 25. As depicted in Fig. 18 and Fig. 24, higher angular velocity of the pipe rotation results in lower damping or negative damping of the system. When the velocity of fluidvis a linear function of time, similar conclusions can be observed in Fig. 20 and Fig. 26, Fig. 21 and Fig. 27 as well as Fig. 22 and Fig. 28. The damping or negative damping is a linear function of time and the frequency of the system is decreasing with time increase. These numerical simulations provide the preparations for the system control.

6 Conclusions

A new scheme of complex modal analysis is proposed for the time-variant dynamical problem of rotating pipe conveying fluid. The explicit semi-analytical solutions are validated by the results obtained from numerical Runge-Kutta method which demonstrates that the proposed method can be applicable for solving time-variant problems. This method outperforms finite difference method by less computation costs and good stability. Moreover, complex eigenvalues obtained in the complex modal analysis can clearly describe the variation tendency of damping (or negative damping)and the frequencies of the system. The proposed method provides a general semi-analytical solution scheme for the similar time-variant dynamical problems.

Acknowledgement: This work is supported by National Natural Science Foundation of China (Project No. 11572229), Shanghai Chenguang Plan (Project No. 14CG18) and Fundamental Research Funds for the Central Universities (Project No. 22120180063).

Agostini, C. E.; Souza, E. C. (2010): Complex modal analysis of a vertical rotor by finite elements method. 9th Brazilian Conference on Dynamics, Control and their Applications, pp. 449-457.

Chellapilla, K. R.; Simha, H. S. (2007): Critical velocity of fluid-conveying pipes resting on two-parameter foundation. Journal of Sound and Vibration, vol. 302, pp.387-397.

Fung, E. H. K.; Yan, D. T. W. (1999): Effects of centrifugal stiffening on the vibration frequencies of a constrained flexible arm. Journal of Sound and vibration, vol. 224, no. 5,pp. 809-841.

Guran, A.; Atanackovic, T. M. (1998): Fluid conveying pipe with shear and compressibility. European Journal of Mechanics, A/Solids, vol. 17, no. 1, pp. 121-137.

Huo, Y.; Wang, Z. (2016): Dynamic analysis of a vertically deploying/retracting cantilevered pipe conveying fluid. Journal of Sound and Vibration, vol. 360, pp. 224-238.

Kessler, C. L. (1999): Complex Modal Analysis of Rotating Machinery (PhD dissertation). Cincinnati University, Cincinnati.

Kraver, T. C.; Fan, G. W.; Shah, J. J. (1996): Complex modal analysis of a flat belt pulley system with belt damping and coulomb-damped tensioner. Journal of Mechanical Design, vol. 118, no. 2, pp. 306-311.

Lee, C. W. (1991): A complex modal testing theory for rotating machinery. Mechanical Systems and Signal Processing, vol. 5, no. 2, pp. 119-137.

Lee, J. F.; Lee, R.; Cangellaris, A. (1997): Time-domain finite-element methods. IEEE Transactions on Antennas & Propagation, vol. 45, no. 3, pp. 430-442.

Li, Y. D.; Yang, Y. R. (2017): Vibration analysis of conveying fluid pipe via He’s variational iteration method. Applied Mathematical Modelling, vol. 43, pp. 409-420.

Matagne, P.; Leburton J. P.; Destine J.; Cantraine G. (2000): Modeling of the Electronic Properties of Vertical Quantum Dots by the Finite Element Method.Computer Modeling in Engineering & Sciences, vol. 1, no. 1, pp. 1-10.

Mitchell,A. R.; Griffiths, D. F. (1980):The finite difference method in partial differential equations. A Wiley-Interscience Publication, John Wiley & Sons, Ltd.,Chichester.

Oliveto, G.; Santini, A.; Tripodi, E. (1997): Complex modal analysis of a flexural vibrating beam with viscous end conditions. Journal of Sound and Vibration, vol. 200, no.3, pp. 327-345.

Paidoussis, M. P.; Luu, T. P.; Prabhakar, S. (2008): Dynamics of a long tubular cantilever conveying fluid downwards, which then flows upwards around the cantilever as a confined annular flow. Journal of Fluids and Structures, vol. 24, pp. 111-128.

Paidoussis, M. P.; Semler, C. (1998): Nonlinear dynamics of a fluid conveying cantilevered pipe with a small mass attached at the free end. International Journal of Non-Linear Mechanics, vol. 33, no. 1, pp. 15-32.

Panussis, D. A.; Dimarogonas, A. D. (2000): Linear in-plane and out-of-plane lateral vibrations of a horizontally rotating fluid-tube cantilever. Journal of Fluids and Structures, vol. 14, pp. 1-24.

Shi, G., Yang, Q.; He, X.; Liew, K. M. (2013): A Three-Dimensional Constitutive Equation And Finite Element Method Implementation for Shape Memory Polymers.Computer Modeling in Engineering & Sciences, vol. 90, no. 5, pp.339-358.

Shi, G.; Lan, K. Y. (1999): Finite element vibration analysis of composite beams based on higher-order theory. Journal of Sound and Vibration, vol. 219, pp. 707-721.

Sorokin, S. V.; Terentiev, A. V. (2003): Nonlinear statics and dynamics of a simply supported nonuniform tube conveying an incompressible inviscid fluid. Journal of Fluids and Structures, vol. 17, pp. 415-431.

Sugiyama, Y.; Katayama, T.; Kanki, E. (1996): Stabilization of cantilevered flexible structures by means of an internal flowing fluid. Journal of Fluids and Structures, vol. 10,pp. 653-661.

Thomsen, J. J.; Dahl, J. (2010): Analytical predictions for vibration phase shifts along fluid-conveying pipes due to Coriolis forces and imperfections. Journal of Sound and Vibration, vol. 329, pp. 3065-3081.

Veletsos, A. S.; Ventura, C. E. (1986): Modal analysis of non-classically damped linear systems. Earthquake Engineering and Structural Dynamics, vol. 14, pp. 217-243.

Wang, L. H.; Hu, Z. D.; Zhong, Z.; Ju, J. W. (2009): Hamiltonian dynamic analysis of an axially translating beam featuring time-variant velocity. Acta Mechanica, vol. 206, no.3-4, pp. 149-161.

Wang, L. H.; Hu, Z. D.; Zhong, Z.; Ju, J. W. (2010): Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length. Acta Mechanica, vol. 214,pp. 225-244.

Wang, L.; Zhong, Z. (2014): Dynamics of the dragonfly wings raised by blood circulation. Acta Mechanica, vol. 225, no. 4-5, pp. 1471-1485.

Wang, L.; Zhong, Z. (2015): Radial basis collocation method for the dynamics of rotating flexible tube conveying fluid. International Journal of Applied Mechanics, vol. 7,no.3, pp. 1550045.

Wang, S.; Liu, Y.; Huang, W. (1998): Research on solid-liquid coupling dynamics of pipe conveying fluid. Applied mathematics and mechanics, vol. 19, no. 11, pp. 1065-1071.

Weiland, T. (1996): Time domain electromagnetic field computation with finite difference methods. International Journal of Numerical Modeling Electronic Networks Devices & Fields, vol. 9, no. 4, pp. 295-319.

Xu, Q.; Prozzi, J. A. (2015): A time-domain finite element method for dynamic viscoelastic solution of layered-half-space responses under loading pulses. Computers &Structures, vol. 160, pp. 20-39.

Yan, Y.; He, X. Q.; Zhang, L. X.; Wang, C. M. (2009): Dynamic behavior of triple-walled carbon nanotubes conveying fluid. Journal of Sound and Vibration, vol. 319,pp. 1003-1018.

Yoon, H. I.; Son, I. S. (2007): Dynamic response of rotating flexible cantilever pipe conveying fluid with tip mass. International Journal of Mechanical Sciences, vol. 49, pp.878-887.