不同弯矩作用下腰椎正常与压缩骨折模型的有限元分析
黄桂雄,罗世兴,纪德朋
有限元分析方法是用于骨科受力分析的一种常用的方法[1-3],因其方便及可重复性,越来越受到国内外学者的青睐。腰椎压缩骨折常导致脊柱失稳,甚至引起脊髓损伤,常见于交通事故或高处坠落[4]。按照压缩的椎体前后高度比,分为三度:Ⅰ度,前后比<1/3;Ⅱ度,前后比约为1/2;Ⅲ度,前后比>2/3。因为腰椎压缩骨折后会造成脊柱不稳,有学者提出,当腰椎压缩骨折类型为II度或III度时应行手术治疗,而I度的压缩骨折则提倡非手术治疗。许多学者对腰椎压缩骨折手术方式进行研究,但对于腰椎I度压缩骨折是否必要行手术治疗仍存在争议[5-6]。本研究通过运用Mimics[7]、 Hypermesh[8]和Abaqus[7]软件构建腰椎正常模型和L2压缩骨折(I度)模型进行对比受力分析,目的是观察在不同弯矩应力下两种模型的椎间盘及关节突的力学分布差异。
资料与方法
1 数据来源
取一位健康男性志愿者,排除腰椎疾病,既往无腰椎骨折及结核等疾病;排除一些有可能影响到腰椎骨质的基础性疾病。采用CT扫描志愿者腰椎,将扫描活动的CT图像以DICOM的格式保存,以便导入相关软件进行建模。
2 相关软件处理
将扫描后的腰椎CT数据,选择L1~3区域的图片,导入Mimics 16.0软件。进行三维重建,将在Mimics软件中生成的腰椎正常模型,并将正常L2椎体上端切割,建立压缩骨折模型;再分别以STL格式导入Hypermesh中进行面网格划分,然后再以STL格式导入Abaqus软件中划分体网格,并建立终板、松质骨及皮质骨[9]集合;椎体、纤维环和髓核材料属性设为各向同性;装配两种模型,并以Spring[10-11]单元模拟建立前纵韧带、后纵韧带、脊间韧带、脊上韧带、黄韧带、横突间韧带及关节囊韧带,并按照相关文献[12-13],赋予韧带、松质骨、皮质骨及终板等物理属性。将腰椎和纤维环、腰椎和髓核之间的关系设为绑定(Tie),上下关节突关节面之间设为面面接触关系,摩擦系数为0.15。接触设置为硬接触。
模拟:工况一,模型在一大小为500N垂直向下作用下,模拟正常人体直立上半身时所受的重力;工况二:工况一与一个弯矩大小为5Nom做前屈运动;工况三:工况一与一个弯矩大小为10Nom做前屈运动;工况四:工况一与一个弯矩大小为15Nom做前屈运动;工况五:工况一与一个弯矩大小为5Nom做后伸运动;工况六:工况一与一个弯矩大小为10Nom做后伸运动;工况七:工况一与一个弯矩大小为15Nom做后伸运动。
3 边界条件
L3椎体和L3椎体双侧下关节突完全固定,并计算在不同工况下不同模型的L1~2椎间盘、L2~3椎间盘、L1关节突、L2关节突和L3关节突受力分布情况,结果用米塞斯应力(Von Mises)表示。
结 果
建立了正常腰椎模型和L2椎体压缩骨折模型,包括皮质骨、松质骨、终板及相关韧带等结构,见图1、2,骨折数据见图3。

图1 正常模型图2 骨折模型图3 L2椎体压缩骨折模型参数
在本实验中,骨折模型的L1~2椎间盘最大应力值可超出正常模型的132.93%,出现在以10Nom前屈运动时;最小可超出正常模型的15.48%,出现在以15Nom做后伸运动时。骨折模型的L2~3椎间盘最大应力值可超过正常模型的66.5%,出现在以15Nom做后伸运动时;最小可超出正常模型的11.59%,出现在直立体位时(图4~6)。骨折模型椎间盘的应力在七种工况下均大于正常模型,并且骨折模型的应力分布部位与正常模型不完全一致(表1、2)。

图4 不同工况下L1~2椎间盘最大应力值

图5 不同工况下L2~3椎间盘最大应力值

表1 L1~2椎间盘最大应力分布部位

表2 L2~3椎间盘最大应力分布部位
在本研究中,骨折模型的关节突在不同弯矩作用下,前屈体位时,L1关节突和L2关节突最大应力值均小于正常模型,而在后伸体位,随着弯矩逐渐增大和关节突位置的降低,出现最大应力值逐渐增大的过程(图6~8)。关节突最大应力的分布部位与正常模型有所差别,分布无明显规律(表3~5)。
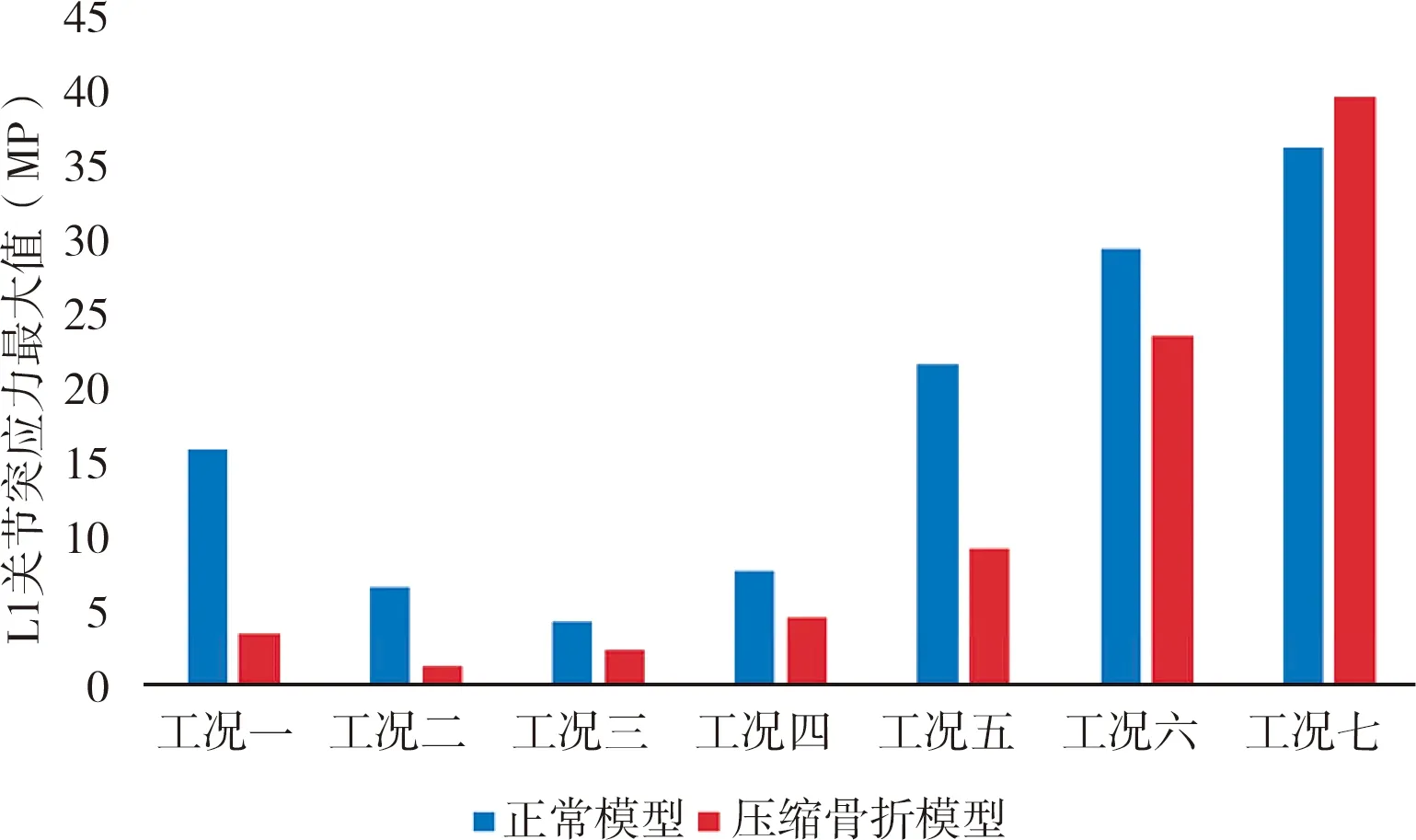
图6 不同工况下L1关节突最大应力值
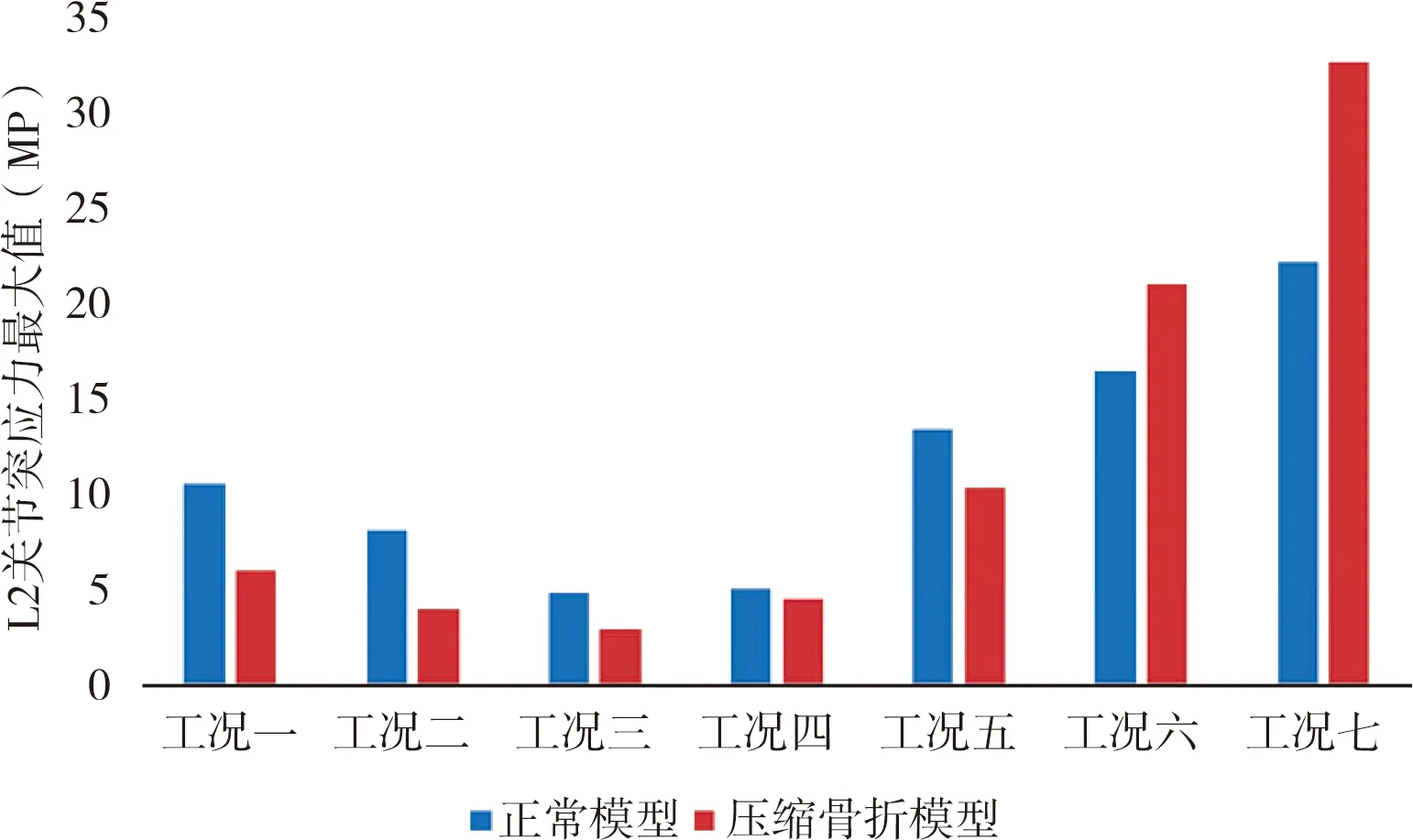
图7 不同工况下L2关节突最大应力值
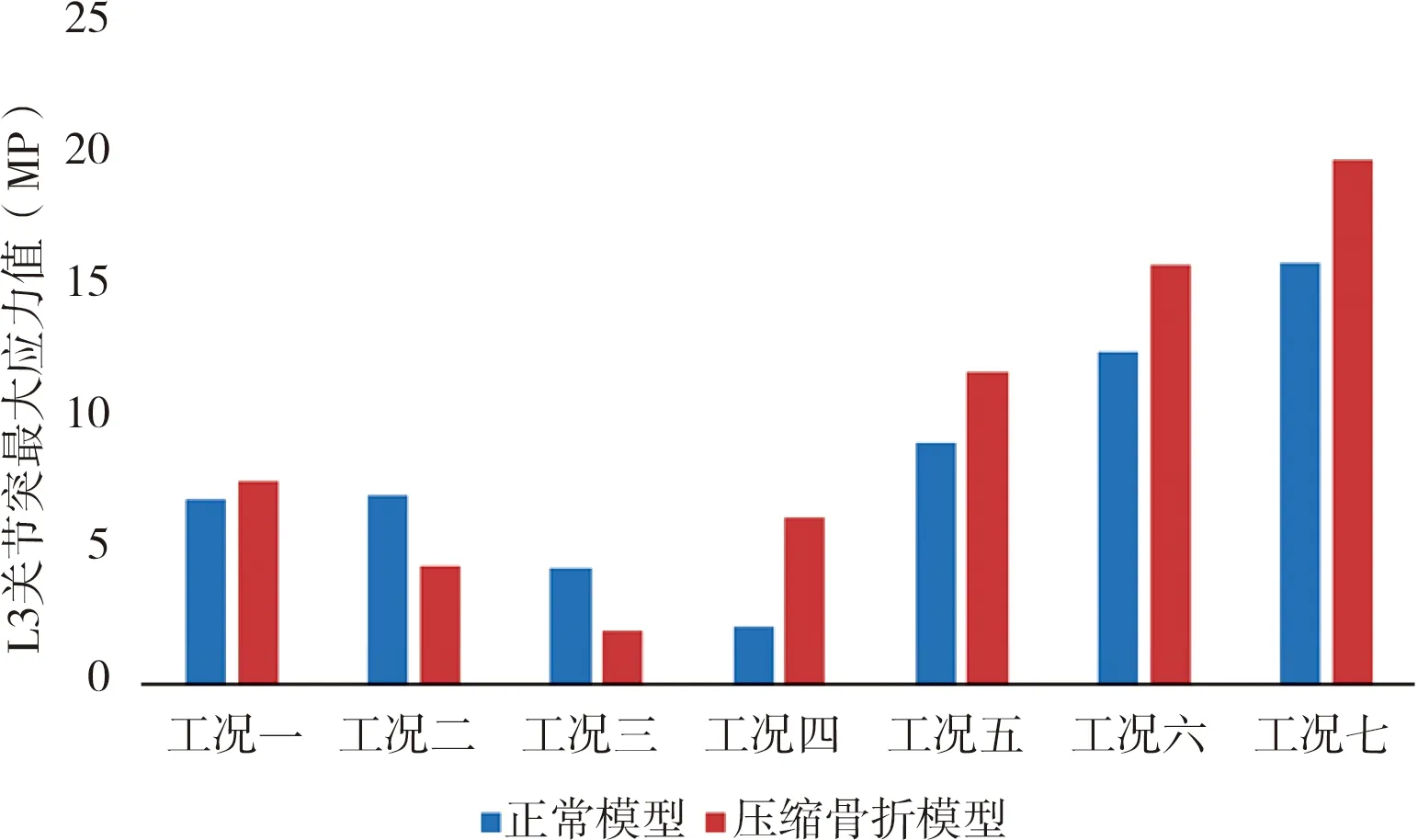
图8 不同工况下L3关节突最大应力值

表3 不同工况下L1关节突最大应力分布部位

表4 不同工况下L2关节突最大应力分布部位

表5 不同工况下L3关节突最大应力分布部位
本研究结果和Chien等[14]的研究结果大致相同,以L1~2椎间盘,在10Nom前屈和后伸的计算结果云图为例(图9、10)。

图9 正常模型在10Nom的弯矩下做前屈运动的云图

图10 骨折模型在10Nom的弯矩下做前屈运动的云图
讨 论
有限元分析[15-16]是医学类特别是骨科受力学分析常用的研究方式。Travert等[17]已运用有限元的方法来分析材料属性和外部载荷对脊柱强度的影响。本研究结合Mimics、Abauqs、Hypermesh软件,建立腰椎的相关模型并进行受力分析,建立L1~3正常腰椎模型和合并L2椎体压缩骨折的L1~3腰椎模型并进行有限元分析,观察在不同弯矩应力下两种模型的椎间盘及关节突的力学分布差异。
本研究结果表明,L2压缩骨折模型在不同的前屈后伸的弯矩作用下其L1~2椎间盘和L2~3椎间盘受到应力为最高。因为应力的增加,最主要的并发症是邻近节段退变[18],从而引起椎间盘突出。Saleem等[19]研究表明,腰椎间盘突出和腰椎管狭窄大多数原因是由于长期腰椎退变和抵抗应力的综合作用的结果。综合学者研究结果,笔者认为腰椎Ⅰ度压缩骨折的患者脊柱的退变可能会加速,甚至将来有可能导致续发骨折[20]。
有研究表明[21]男性比女性更容易因为机械应力的增加而损害腰椎间盘。本研究结果表明,随着前屈和后伸的弯矩增大,大部分模型的椎间盘受到的应力均增大,前屈的动作较后伸的动作增大更明显,这就验证了前屈的动作会增加腰椎间盘突出的概率。从事重体力活动且伴有频繁弯腰动作容易出现腰椎间盘突出,并且胸腰段脊柱是整个脊柱的应力集中部位,容易发生骨折,尤其在骨质疏松的老年人多见[22]。
在不同弯矩的作用下,前屈运动时大部分应力位于椎间盘的前右侧,这是因为人体在受向前运动弯矩的作用下,重力也向前移动,而因为惯用右手的人,脊柱的上胸椎偏向右,而腰椎则代偿性凸向左侧[23],所以重心偏向右侧,导致右侧受应力大于左侧;当在后伸的弯矩作用下,应力的分布偏向后右侧的原理也如此,说明了临床上有些患者腰椎间盘突出偏向右的原因。
本研究中,在直立状态下腰椎压缩骨折模型椎间盘的应力明显大于正常模型的应力,而大部分骨折模型的关节突在前屈时应力较正常模型小;在不同的体位和不同的弯矩大小作用下,骨折模型在不同节段的关节突应力成分考虑为关节突和椎弓根受前屈到后伸的体位改变的影响,分别为关节突压应力减小,椎弓根到拉应力增大,再转变为关节突压应力增大的过程;说明腰椎压缩骨折后,关节突应力的大小和后伸的幅度和关节突的节段均有关,并且在骨折模型中,应力增大的关节突,因为力学机制的变化,有可能对关节突本身产生不利的影响。笔者认为,在直立体位时骨折模型的关节突应力最大值较正常模型的大,可能是腰椎压缩骨折后,脊柱后凸畸形,导致脊柱重心向前,即重力的向前水平分力增加,后部受水平分力减少,相应的应力也减小。所以可推测,椎间盘和关节突的应力大小与椎体的形状可能相关。再者,腰椎压缩骨折时,由于压缩的椎体横截面积发生改变[24],导致应力集中分布于椎体压缩骨折皮质骨的前上半部。L1~2椎间盘的应力分布>L2~3椎间盘的原因,有可能是应力分布以L2压缩骨折上终板前端和皮质骨交界处为中心,离该中心越远,相同的材料属性,应力相对越小。在不同前屈和后伸的弯矩作用下,两种模型的椎间盘在前屈时应力增加幅度较大,说明前屈的动作对椎间盘的损害较大;后伸时椎间盘应力变化不明显,考虑为椎体后部的杨氏模量值较椎间盘的值大,应力主要由椎体后部结构承担,这就是应力遮挡的原理[25]。所以前屈时,椎体重心前移,脊柱骨皮质的杨氏模量值较大,承担了大部分应力,所以腰椎后部的关节突应力变化不明显。L1、L2和L3关节突最大应力分布情况,大部分分布在右下关节突关节面的上方,部分分布在椎弓根,这就可能导致关节突关节因为应力集中容易退变[26-27]。
本研究假设在腰椎所能承受的应力范围内进行分析,不考虑各个材料的塑性区和断裂区。结果表明,压缩骨折模型腰椎间盘和部分腰椎关节突的应力较正常模型大。在生理活动下,由于高周疲劳(high-cycle fatigue,是指材料在低于其屈服强度的循环应力作用下,经10 000~100 000以上循环次数而产生的疲劳。高周疲劳的特点是作用于零件或构件的应力水平较低)[24],有压缩骨折病史的患者再发生骨折的可能性大。
综上所述,有限元力学分析显示腰椎压缩骨折后,伤椎的椎间盘和关节突的压应力较正常椎体增大,提示骨折后可能脊柱退变加速。相对关节突,椎间盘的应力分布较规律,关节突应力分布的不规律可能提示骨折后脊柱后柱退变加速具体部位具有不确定性。
[1] Divya VA,Edward KW,Ronald AL,et al.Bilateral pedicle screw fixation provides superior biomechanical stability in transformational lumbar interbody fusion: a finite element study [J].Spine J,2015,15(8):1812-1822.
[2] Bisschop A,Holewijn RM,Kingma I,et al.The effects of single-level instrumented lumbar laminectomy on adjacent spinal biomechanics[J].Global Spine J,2015,5(1):39-48.
[3] Agarwal A,Zakeri A,Agarwal AK,et al.Distraction magnitude and frequency affects the outcome in juvenile idiopathic patients with growth rods: finite element study using a representative scoliotic spine model[J].Spine J,2015,15(8):1848-1855.
[4] Ivancic PC.Biomechanics of thoracolumbar burst and chance-type fractures during fall from height[J].Global Spine J,2014,4(3):161-168.
[5] Dohm M,Black CM,Dacre A,et al.A randomized trial comparing balloon kyphoplasty and vertebroplasty for vertebral compression fractures due to osteoporosis [J].AJNR Am J Neuroradiol,2014,35(12):2227-2236.
[6] Saracen A,Kotwica Z.Treatment of multiple osteoporotic vertebral compression fractures by percutaneous cement augmentation[J].Int Orthop,2014,38(11):2309-2312.
[7] Faraipour H,Jamshidi N.Effects of different angles of the traction table on lumbar spine ligaments: a finite element study[J].Clin Orthop Surg,2017,9(4):480-488.
[8] Filardi V,Simona P,Cacciola G,et al.Finite element analysis of sagittal balance in different morphotype: forces and resulting strain in pelvis and spine[J].J Orthop,2017,14(2):268-275.
[9] Garo A,Arnoux PJ,Wagnac E, et al.Calibration of the mechanical properties in a finite element model of a lumbar vertebra under dynamic compression up to failure[J].Med Biol Eng Comput,2011,49(12):1371-1379.
[10] Jung TG,Woo SH,Park KM,et al.Biomechanical behavior of two different cervical total disc replacement designs in relation of concavity of Articular Surfaces: ProDisc-C®VS Prestige-LP®[J].Int J Prec Eng Manufac,2013,14(5):819-824.
[11] Clin J,Aubin CE,Lalonde N,et al.A new method to include the gravitational forces in a finite element model of the scoliotic spine[J].Med Biol Eng Comput,2011,49(8):967-977.
[12] Goel VK,Monrone BT,Gilbertson LG,et al.Interlaminar shear stresses and laminae separation in a disc: finite element analysis of the L3-4motion segment subjected to axial compressive loads[J].Spine,1995,20(6):689-698.
[13] Jones AC,Wilcox RK.Finite element analysis of the spine: towards a framework of verification,validation and sensitivity analysis[J].Med Eng Phys,2008,30(10):1287-1304.
[14] Chien CY,Kuo YJ,Lin SC,et al.Kinematic and mechanical comparisons of lumbar hybrid fixation using dynesys and cosmic systems[J].Spine(Phila Pa 1976),2014,39(15):E878-884.
[15] Imai K.Analysis of vertebral bone strength,fracture pattern,and fracture location: a validation study using a computed tomography-based nonlinear finite element analysis[J].Aging Dis,2014,6(3):180-187.
[16] 延东,毛景松,石先明,等.不同载荷下腰1椎体内应力分布规律的有限元分析[J].中国脊柱脊髓杂志,2014,24(9):882-887.
[17] Travert C,Jolivet E,Sapin-de Brosses E,et al.Sensitivity of patient specific vertebral finite element model from low dose imaging to material properties and loading conditions[J].Med Biol Eng Comput,2011,49(12):1355-1361.
[18] Palepu V, Kodigudla M,Goel VK.Biomechanics of disc degeneration[J].Adv Orthop,2012,2012:1-17.
[19] Saleem S,Aslam HM,Rehmani MA,et al.Lumbar disc degeneration disease: disc degeneration symptoms and magnetic resonance image findings[J].Asian Spine J,2013,7(4):322-334.
[20] Ren HL,Jiang JM,Chen JT,et al.Risk factors of new symptomatic vertebral compression fractures in osteoporotic patients undergone percutaneous vertebroplasty[J].Eur Spine J,2015,24(4):750-758.
[21] Wang YX,Griffith JF.Effect of menopause on lumbar disk degeneration: potential etiology[J].Radiology,2010,257(2):318-320.
[22] Bouza C,López-Cuadrado T,Almendro N,et al.Safety of balloon kyphoplasty in the treatment of osteoporotic vertebral compression fractures in Europe: a meta-analysis of randomized controlled trials[J].Eur Spine J,2015,24(4):715-723.
[23] 柏树令.系统解剖学[M].2版.北京:人民卫生出版社,2013:37-44.
[24] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2004:1-27.
[25] Zhao J,Chen LJ,Yu K,et al.Effects of chitosan coating on biocompatibility of Mg-6%Zn-10% Ca3(PO4)2implant[J].Trans Nonferrous Met Soc China ,2015,25(3):824-831.
[26] Rohlmann A,Lauterborn S,Dreischarf M,et al.Parameters influencing the outcome after total disc replacement at the lumbosacral junction.Part 1: misalignment of the vertebrae adjacent to a total disc replacement affects the facet joint and facet capsule forces in a probabilistic finite element analysis[J].Eur Spine J,2013,22(10):2271-2278.
[27] Park WM,Kim K,Kim YH.Changes in range of motion,intradiscal pressure,and facet joint force afterintervertebral disc and facet joint degeneration in the cervical spine[J].J Mech Sci Technol,2015,29 (7): 3031-3038.

