基于稀疏表示和多成分字典学习的超分辨率重建

徐志刚, 李文文, 袁飞祥, 朱红蕾, 许亚美

(兰州理工大学计算机与通信学院, 甘肃 兰州 730050)

0 引 言

随着图像处理与分析技术的飞速发展,人们对高分辨率图像和视频信息的需求日益增长。但是,由于硬件条件、成本及成像环境等因素的影响,图像的空间分辨率往往较低,不能满足实际应用的需要。图像超分辨率重建技术通过软件处理手段来获取满足应用需求的高分辨率图像,不必改变现有硬件系统,在成本上和技术上具有较大优势,因此近年来在遥感监测、医学成像、公共安全等领域得到了广泛的研究与应用[1-4]。

单帧图像超分辨率重建方法是近年来图像超分辨率重建研究的主要领域，基于稀疏表示的方法是目前单帧图像超分辨率重建研究的热点[5-7]。

文献[8]利用输入低分辨率(low resolution,LR)图像块和待重建高分辨率(high resolution,HR)图像块在特定字典对下具有相同稀疏系数的先验约束来重建高分辨率图像,获得了较好的重建结果。文献[9]提出利用高斯混合模型聚类算法对训练图像块进行聚类,然后使用改进字典更新方式的K-奇异值分解 (K-singular value decomposition,K-SVD)算法来快速获得高、低分辨率字典对,从而改善基于字典学习的图像超分辨率重建效果欠佳的问题。文献[10]利用图像形态分量分析(morphological component analysis,MCA)方法将输入LR图像分解为结构部分和纹理部分。对于结构部分采用新边缘导向插值(new edge-directed interpolation,NEDI)算法重建。而对于纹理部分,则采用基于稀疏模型的方法进行重建。文献[11]在稀疏字典重建模型基础上引入图像的非局部自相似性和超拉普拉斯先验作为正则化约束,由此增强了稀疏模型的有效性。

上述算法都是基于单字典的稀疏重建方法。这类方法实现较为简单,重建效果总体良好。但是,在表征复杂自然图像中不同形态细节信息等方面仍可进一步改进。

为解决基于单字典稀疏重建方法存在的问题,更好地恢复重建图像高频细节信息,文献[12]将输入LR图像分解为结构分量和纹理分量,并分别采用稀疏表示方法对它们进行重建,然后再融合生成HR重建图像。文献[13]在利用多字典重建图像时,采用多成分Gabor字典来表征图像的平滑、结构和纹理特征,能够提高图像特征表达能力。文献[14]在设计基于自适应多字典学习的单幅图像超分辨率重建算法时,对低分辨率图像金字塔结构中的图像块进行聚类,并在聚类结果引导下对训练样本库中的图像块进行分类,然后利用各类样本分别构建针对不同类的多个字典,从而能够确定表达重建图像块的最优字典。

多字典稀疏重建方法在增强稀疏字典的自适应能力、有效表征和恢复待重建LR图像边缘细节信息方面表现更好一些。但是,这类方法的计算复杂度相对较高。

基于上述分析,为了提升重建算法对于输入LR图像边缘及纹理细节信息的保持与恢复能力,消除重建HR图像容易出现的块效应和模糊伪影,在文献[12,15]的基础上提出基于稀疏表示和多成分字典学习的超分辨率重建算法。该算法利用MCA方法将图像分解为纹理层和结构层,并分别构造纹理、结构分量稀疏表示字典。在提取图像特征时,对纹理层图像采用Gabor变换方法进行特征提取。同时在训练字典和重建过程中,利用L1/2正则模型构造约束项。对于重建图像,再利用全局约束与非局部相似性约束相结合的方式进行优化。实验结果表明,该算法在重建图像的主观视觉效果上有一定改善,同时在客观评价指标上有较显著的提升。

1 本文算法

1.1 算法设计

本文算法可以分为两部分。第1部分是基于L1/2正则模型的结构、纹理多成分重建字典构造。第2部分是基于多成分字典的单幅图像超分辨率重建。算法具体流程图如图1和图2所示。

1.2 基于MCA的图像结构、纹理信息提取

图像MCA方法假设图像包含多种形态特征分量,并且每种形态在对应的字典下可以稀疏表示,而该字典对其他的形态特征不具有稀疏性。借助对应的稀疏字典就可以获得图像的结构、纹理层信息[16]。

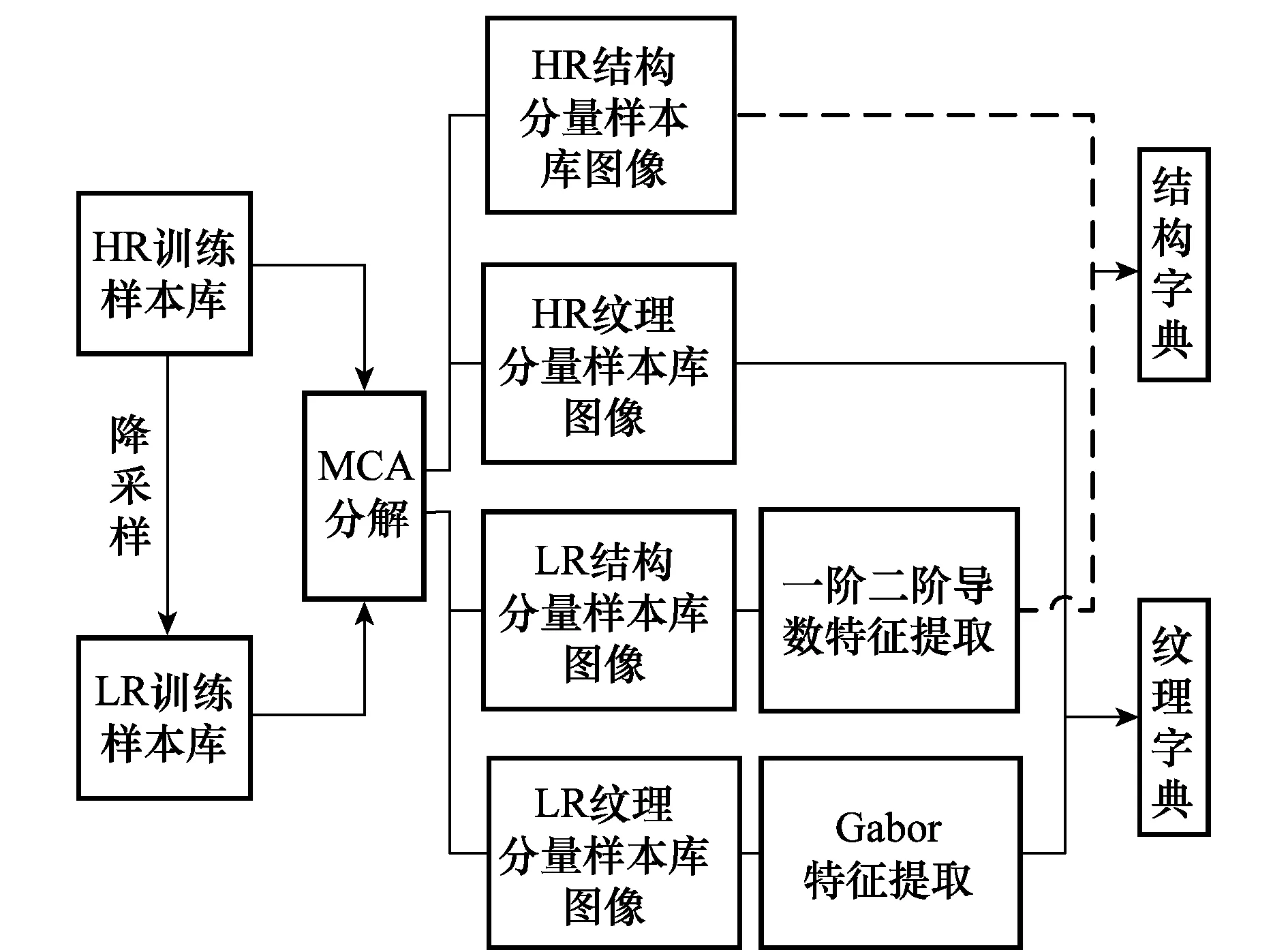
图1 字典训练Fig.1 Dictionary training

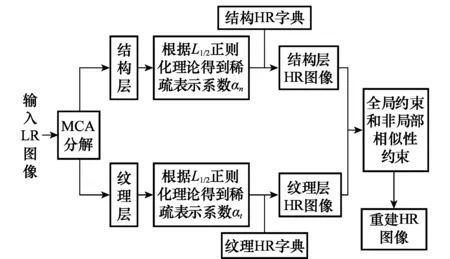
图2 图像重建Fig.2 Image reconstruction

设待处理的图像F由包含纹理层Ft和结构层Fn的分量图像叠加形成,即F=Ft+Fn,并可稀疏表示为

Ft=Dtαt

(1)

Fn=Dnαn

(2)

式中,αt、αn是在纹理、结构冗余字典Dt、Dn下的稀疏表示系数。

1.3 利用Gabor变换提取纹理层图像特征

在图像重建过程中,特征提取对图像重建的质量具有重要意义。为了使训练的字典能更好地匹配输入LR图像,提高重建HR图像质量,选择有效的特征提取方法是必要的。对自然图像和纹理/结构层图像使用一阶二阶导数方法进行特征提取是常规做法[8,12]。总体而言,对于图像结构信息,一阶二阶导数方法可以较好地实现特征提取。但是,由于纹理层图像包含大量的中高频细节信息,采用一阶二阶导数方法难以全面有效地对这些信息进行表征。所以,应该使用更有针对性的方法进行特征提取。

Gabor变换具有良好的空域局部化特征,是重要的纹理特征提取与表示工具。利用Gabor变换对图像纹理边缘敏感,能够提供良好的空间局部性和方向选择性的特点,可以有效地描述图像的纹理信息。而且Gabor变换对光照、姿态具有一定的鲁棒性,其处理的数据量较少。因此,本文对经过MCA分解的结构层图像采用一阶二阶导数进行特征提取,而对纹理层图像则采用Gabor变换特征提取方法。Gabor核函数的定义为

(3)

式中,(x,y)为坐标位置;σ为高斯函数标准差;k确定了Gabor的尺度;θ确定了Gabor函数的方向。本文中,θ选取π/4、π/2、3π/4和π四组值来进行特征提取。

1.4 基于L1/2正则模型构造字典学习算法

在对字典进行训练时,文献[8]和文献[12]均采用基于L1正则约束的方法

D=minα,D‖Y-Dα‖2+λ‖α‖1

(4)

但是,文献[17]指出,相对于L1正则约束,L1/2正则约束的解更稀疏,且更稳定。因此,本文采用L1/2正则约束模型[18],并采用联合字典训练方法来构造高低分辨率结构、纹理字典对，即

Di=minαi,Di‖Yi-Diαi‖2+λ‖αi‖1/2,i=t,n

(5)

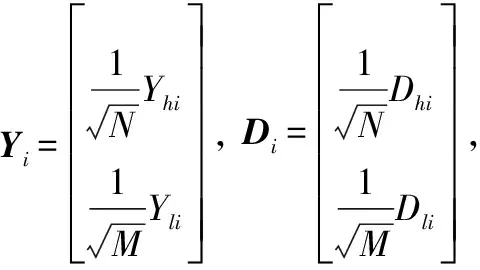
1.5 重建图像约束优化

在得到多成分稀疏字典对(Dhi,Dli)(i=t,n)后,利用基于L1/2稀疏正则模型的多成分字典超分辨率重建方法就可以得到输入LR图像Y的重建HR图像X。

但是,在重建过程中由于噪声、匹配误差等因素的影响,基于块的稀疏重建方法在重建HR图像中容易出现块效应及模糊伪影[20]。考虑到常规的反向投影全局优化模型难以更有效地保持重建图像局部区域的边缘纹理细节,而非局部相似性先验约束则可以非局部图像块相似性为基础,通过图像块匹配方法在图像一定的邻域内搜索与当前图像块相似的图像块,然后利用匹配图像块间的权重作为先验知识来更好地保持图像的细节信息。因此,为了更好地消除重建图像的块效应和模糊伪影,本文在反向投影全局优化模型的基础上引入非局部相似性先验约束[21]来优化HR图像。本文的全局约束和非局部自相似约束模型为

(6)

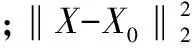
(7)

式中,N(xi)表示图像中第i个图像块;N(xj)表示搜索到的与N(xi)相似的块;h为衰减因子;z(i)表示归一化参数。

(8)

2 实验分析

为了验证本文算法性能,采用峰值信噪比(peak signal-to-noise ratio,PSNR)作为客观评价指标来评价重建图像质量，表示为

(9)

式中,r表示重建HR图像;f表示原始HR图像;MSE(·)表示r和f的均方误差(mean squared error,MSE)函数，表示为

(10)

式中,MN表示图像总像素数;rij和fij表示重建后的HR图像和原始HR图像在点(i,j)处的像素值。

为了验证和分析算法的性能,利用双三次插值(Bicubic)、文献[8]算法(sparse coding super-resolution,ScSR)、文献[12]算法(multi-morphology super-resolution,MmSR)和本文算法来对比图像重建质量。在测试上述算法性能时,利用文献[3,22]采用的Set5和Set14集中的图像作为测试对象。

为了便于比较,本文算法实验所采用的训练样本库与文献[8]和文献[12]相同。LR图像块大小为5×5,图像块之间的像素重叠为4,迭代次数为20,字典大小为1 024。

部分设置了3组实验,分别针对上采样因子为2和3以及上采样因子为2,但LR图像受高斯噪声污染的情况展开。

实验1设置上采样因子为2。表1给出了利用Bicubic算法、ScSR算法、MmSR算法和本文算法重建图像的PSNR对比。

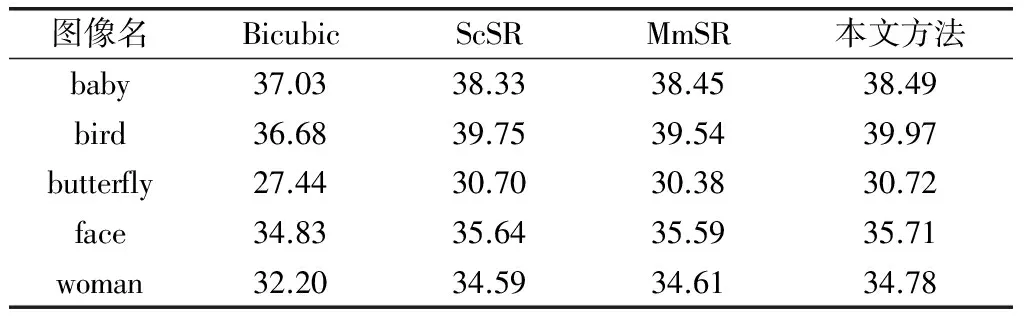
表1 重建图像PSNR值对比

图3为实验1中bird图像的重建对比结果。其中,图3(a)为LR图像,图3(b)为原始HR图像,图3(c)为Bicubic算法重建结果,图3(d)为ScSR算法重建结果,图3(e)为MmSR算法重建结果,图3(f)为本文算法重建结果。由图3中bird的眼睛部位可以看到,Bicubic算法得到的重建结果模糊现象比较明显。ScSR算法得到的结果图像细节相对清晰,但在边缘区域仍有一些模糊和伪影现象存在。而MmSR算法得到的重建图像边缘区域的模糊和伪影现象有一定程度减弱。对比前述算法,本文算法重建图像的边缘轮廓更加清晰,图像的视觉效果得到了改善。

图3 Bird图对比实验结果Fig.3 Compared with the experimental results of the bird image

实验2设置上采样因子为3。表2给出了利用Bicubic算法、ScSR算法、MmSR算法和本文算法重建图像的PSNR对比。从表2中可以看到,随着上采样倍数的增加,各算法的PSNR值普遍呈现下降趋势。

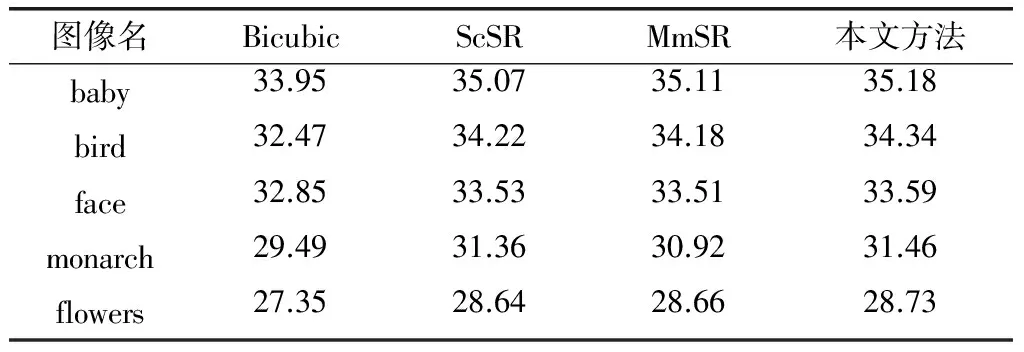
表2 重建图像PSNR值对比

实验2中monarch图像的重建对比结果如图4所示。

图4 Monarch图对比实验结果Fig.4 Compared with the experimental results of the monarch image

由图4中monarch图像的翅膀部位可以看到,Bicubic算法重建的图像存在比较严重的模糊,边缘区域的锯齿现象也最明显。ScSR算法重建图像的质量较好,但边缘区域仍然存在较明显的伪影。MmSR算法重建图像相对于Bicubic算法模糊程度减轻,但重建图像的边缘区域重建效果不甚理想。而本文算法在提升重建图像清晰度的同时更好地抑制了伪影现象。

实验3设置上采样因子为2,但LR图像受均值为0,均方差为0.001的高斯噪声污染。考虑到ScSR算法、MmSR算法和本文算法在重建算法设计中均未将去除LR图像噪声作为重点研究内容,因此,本文先利用双边滤波方法[23]去除LR图像噪声,然后再使用上述3种方法进行重建。表3给出了利用ScSR算法、MmSR算法和本文算法重建图像的PSNR对比。从表3中可以看到,3种算法重建结果的PSNR值相对于表1均有较大幅度的降低。

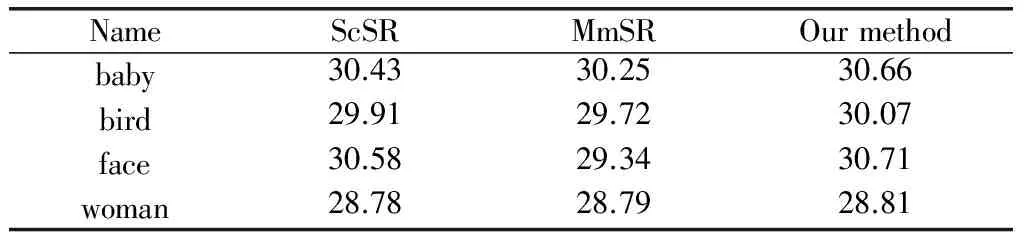
表3 重建图像PSNR值对比

实验3中face图像的重建对比结果如图5所示。

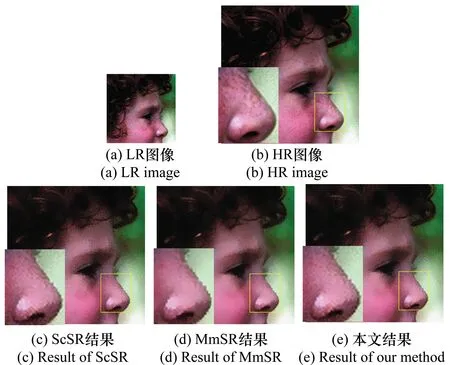
图5 Face图对比实验结果Fig.5 Compared with the experimental results of the face image

由图5中face图像的鼻子部位可以看到,由于受高斯噪声污染,尽管经过双边滤波去噪,但是ScSR算法、MmSR算法和本文算法重建结果中边缘区域的光滑程度均有较大程度的弱化。但相对而言,本文算法在图像细节恢复和图像伪影消除方面表现较好。

3 结 论

为了解决基于稀疏表示模型的图像超分辨率重建方法难以有效提升图像高频信息恢复能力,易产生视觉伪影的问题,提出基于稀疏表示和多成分字典学习的超分辨率重建方法。该方法在利用MCA方法构建结构和纹理多成分重建字典时,分别利用一阶二阶导数和Gabor变换提取结构和纹理特征。采用L1/2正则模型用于字典训练和图像重建。同时,采用全局约束与非局部相似性约束模型对重建图像进行优化。实验结果表明,该方法在消除重建HR图像视觉伪影,保持和恢复重建HR图像边缘细节信息方面有较好的表现。

[1] FU W, LI S, FANG L, et al. Adaptive spectral-spatial compression of hyperspectral image with sparse representation[J]. IEEE Trans.on Geoscience and Remote Sensing, 2017, 55(2): 671-682.

[2] MANDAL S, BHAVSAR A, SAO A. Noise adaptive super-reso-lution from single image via non-local mean and sparse representation[J]. Signal Processing, 2017, 132: 134-149.

[3] DONG C, LOY C, HE K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307.

[4] LIU D, WANG Z, WEN B, et al. Robust single image super-resolution via deep networks with sparse prior[J]. IEEE Trans.on Image Processing, 2016, 25(7): 3194-3207.

[5] DONG W, FU F, SHI G, et al. Hyperspectral image super-reso-lution via non-negative structured sparse representation[J]. IEEE Trans.on Image Processing, 2016, 25(5): 2337-2352.

[6] UIBOUPIN T, RASTI P, ANBARJAFARI G, et al. Facial image super resolution using sparse representation for improving face recognition in surveillance monitoring[C]∥Proc.of the Signal Processing and Communication Application Conference, 2016: 437-440.

[7] AHMADI K, SALARI E. Single-image super resolution using evolutionary sparse coding technique[J]. IET Image Processing, 2017, 11(1): 13-21.

[8] YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Trans.on Image Processing, 2010, 19(11): 2861-2873.

[9] 詹曙, 方琪, 杨福猛, 等. 基于耦合特征空间下改进字典学习的图像超分辨率重建[J]. 电子学报, 2016, 44(5): 1189-1195.

ZHAN S, FANG Q, YANG F, et al. Image super-resolution reconstruction via improved dictionary learning based on coupled feature space[J].Acta Electronica Sinica,2016,44(5):1189-1195.

[10] 管超,金波,张爱新.基于MCA分解的超分辨率重构算法[J].通信技术, 2013, 46(3): 87-90.

GUAN C, JIN B, ZHANG A. MCA-based image super resolution[J]. Communications Technology, 2013, 46(3): 87-90.

[11] 李娟, 吴谨, 陈振学, 等. 基于自学习的稀疏正则化图像超分辨率方法[J]. 仪器仪表学报, 2015, 36(1): 194-200.

LI J, WU J, CHEN Z, et al. Self-learning image super-rsolution method based on sparse representation[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 194-200.

[12] LIU W, LI S. Multi-morphology image super-resolution via sparse representation[J]. Neurocomputing, 2013, 120(10): 645-654.

[13] 刘梓, 宋晓宁, 於东军, 等. 基于多成分字典和稀疏表示的超分辨率重建算法[J]. 南京理工大学学报(自然科学版), 2014, 38(1): 1-5.

LIU Z, SONG X, YU D, et al. Super-resolution reconstruction algorithm based on multi-component dictionary and sparse representation[J]. Journal of Nanjing University of Science and Technology (Natural Science Edition), 2014, 38(1): 1-5.

[14] 潘宗序, 禹晶, 肖创柏, 等. 基于自适应多字典学习的单幅图像超分辨率算法[J]. 电子学报, 2015, 43(2): 209-216.

PAN Z, YU J, XIAO C, et al. Single image super resolution based on adaptive multi-dictionary learning[J]. Acta Electronica Sinica, 2015, 43(2): 209-216.

[15] 徐志刚,李文文.基于多字典L1/2正则化的超分辨率重建算法[J].吉林大学学报(信息科学版), 2017, 35(3): 354-362.

XU Z, LI W. Super-Resolution reconstruction based onL1/2regularization of multi component dictionary[J]. Journal of Jilin University(Information Science Edition), 2017, 35(3): 354-362.

[16] STARCK J L, ELAD M, DONOHO D L. Image decomposition via the combination of sparse representations and a variational approach[J].IEEE Trans.on Image Processing,2005,14(10):1570-1582.

[17] XU Z, CHANG X, XU F, et al.L1/2regularization: a thresholding representation theory and a fast solver[J]. IEEE Trans.on Neural Networks and Learning Systems,2012,23(7):1013-1027.

[18] 徐志刚,李文文,朱红蕾,等.一种基于L1/2正则约束的超分辨率重建算法[J].华中科技大学学报(自然科学版),2017,45(6): 38-42.

XU Z, LI W, ZHU H, et al. Super-resolution reconstruction based on L1/2regularization[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2017,45(6):38-42.

[19] 谢林林. 一种快速求解L1/2正则化问题的新算法[D]. 大连：大连理工大学, 2014.

XIE L. A new algorithm for fast solvingL1/2regularization problem[D]. Dalian: Dalian University of Technology, 2014.

[20] ZHANG J, XIONG R, CHEN Z, et al. Concolor: constrained non-convex low-rank model for image deblocking[J]. IEEE Trans.on Image Processing, 2016, 25(3): 1246-1259.

[21] XU Z, WANG X, CHEN Z, et al. Nonlocal similarity based dem super resolution[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 110: 48-54.

[22] DONG C, LOY C, HE K, et al. Learning a deep convolutional network for image super-resolution[C]∥Proc.of the European Conference on Computer Vision, 2014: 184-199.

[23] SANKARAN K S, AMMU G, NAGARAJAN V. Patch based image restoration using adaptive bilateral filtering[C]∥Proc.of the International Conference on Information Communication and Embedded Systems,2014:1-5.