拦截导弹的制导律辨识与弹道预报

胡志恒, 周 荻, 邹昕光

(1. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001; 2. 哈尔滨工业大学电气工程及自动化学院, 黑龙江 哈尔滨 150001)

0 引 言

近几十年来,导弹制导律的研究取得了许多成果。从经典的比例导引律到增广比例导引律,再到各种现代制导律。导弹制导律的不断改进,给导弹规避方提出了更大的挑战。单纯对导弹运动参数进行观测已经不能满足要求,因此产生了识别制导律的新思路,即利用我方观测器对敌方拦截导弹的外部观测数据,对敌方拦截导弹的制导律进行辨识和参数估计。与传统的弹道预报相比,可以得到对方拦截导弹未来加速度的变化规律,从而建立更精确的运动模型,对未来位置进行更精确的预报,对于机动突防和反拦截有着重要意义。

制导律辨识问题中,由于制导律的多样性,识别问题的难点在于构造统一的通用数学模型,对制导行为进行描述。文献[1]假设敌方拦截导弹使用比例导引律,然后以比例导引系数作为未知量建立观测数据方程,通过求解制导控制量方程得到制导律参数。文献[2]的仿真结果表明,对于未知的制导律同样可以假设为比例导引律,通过调整比例导引系数拟合任意未知的制导律。为了滤除测量噪声对识别结果造成的影响,用取均值的简易滤波方法对数据进行了处理,提高了识别结果的精确度和稳定性。文献[3]令观测方进行某种机动,通过参照模型库辨识大气层外拦截器的导航比。文献[4]采用交互多模型(interacting multiple model, IMM)思想,基于扩展卡尔曼滤波(extended Kalman filter, EKF)算法和CV、CJ、CA模型,实现对来袭导弹的状态估计。文献[5]通过线性化导引律方程,利用多模型自适应估计(multiple model adaptive estimation, MMAE)思想,实现了二维平面内的导引律辨识。文献[6]采用无迹卡尔曼滤波(unscented Kalman filter, UKF)方法和MMAE方法,设计了导弹的导引律及参数辨识器,在三维坐标内实现了对多种制导律及参数的辨识。文献[7]从决策的角度研究了拦截末端导弹导引律的辨识问题,文献[8]研究了自动寻的导弹三自由度拦截的导弹导引律辨识问题。

在实际应用中,制导律通常采用零化视线角速率的思想,其都可以等效为不同导航系数的比例导引律。因此,用比例导引律作为制导律的模型,把制导律辨识问题转化为比例导引律的参数辨识问题。

系统的可观性是滤波器设计的理论前提,但是在前述制导律辨识的研究中并没有对该问题从理论上给出严格的证明。

非线性系统的可观性问题比较复杂,通常的做法是将其局部线性化,然后利用线性系统的可观性理论进行研究。文献[9]对非线性系统可观性理论的发展做了详细的介绍;文献[10]利用微分几何理论,提出了“局部弱可观”概念,为非线性系统可观性理论分析做出了重大贡献。

弹道预报主要分为两个问题:通过滤波估计目标的位置和速度,提高滤波的精度,为预报提供准确的初值;为目标运动建立准确的预报模型,得到准确的预报结果。

目前关于弹道预报问题也已经有了不少研究,但是研究对象多为弹道导弹。文献[11]使用基于当前统计模型和UKF进行估计,然后用修正的动力学模型进行预报。文献[12]使用基于IMM算法的UKF算法估计弹道系数。

传统的弹道导弹在大气层外时做惯性运动，进入大气层后主要受气动力作用，故其运动模型容易建立。当预测目标有主动机动时,模型建立比较困难。而本文研究的内容中,预测目标的加速度受到制导律约束。因此,用待定制导系数的比例导引律拟合预测目标的制导律,可以得到未来加速度的变化规律,从而实现对未来轨迹更精确的估计。

1 问题描述

考虑三维平面内导弹拦截目标的问题。在本文研究的问题中,导弹是敌方,目标是我方。建立坐标系如图1所示,我方惯性坐标系Txyz,原点T为我方初始位置,Tx轴指向敌方初始位置,Ty轴铅垂向上,Tz轴由右手定则确定；敌方惯性坐标系Mxyz,原点M为敌方初始位置,Mx轴指向我方初始位置,My轴铅垂向上,Mz轴由右手定则确定。为处理敌方导弹制导律,建立敌方的视线坐标系Mxsyszs,原点M为敌方位置,Mxs轴指向我方,即敌方的视线方向,Mys轴在铅垂平面内垂直于视线指向上,Mzs轴由右手定则确定。由敌方的惯性坐标系和视线坐标系可以定义两个视线角qε、qβ。

图1 坐标系关系图Fig.1 Relation of coordinates

将系统状态变量取为

式中,rx、ry、rz为目标-导弹位置在我方惯性系下的分量;vx、vy、vz为目标-导弹速度在我方惯性系下的分量;axm、aym、azm为导弹的制导加速度在我方惯性系下的分量;Ny、Nz为导弹俯仰、偏航两通道的制导系数。则系统状态方程为

(1)

式中,axt、ayt、azt为目标的机动加速度在我方惯性系下的分量;uxm、uym、uzm为导弹制导指令在我方惯性系下的分量;τ是导弹动态特性的时间常数。

按照比例导引律,视线系下导弹的制导指令为

(2)

式中,r、qε、qβ分别是目标-导弹的相对距离和俯仰、偏航视线角。

为简化方程形式,对制导律进行解耦。在俯仰平面内,比例导引律的制导指令在视线系下为

(3)

式中

由视线系到我方惯性系的转换矩阵为

(4)

式中

于是导弹加速度指令在我方惯性系下为

(5)

类似地,得到偏航平面

(6)

代入式(1)得到完整的状态方程表达式。

目前,在对敌方防空反导导弹的近程探测预警系统中,被动探测方式依然是主流,但是随着激光雷达的发展,主动探测方法也变得可行。

激光雷达是传统雷达技术与现代激光技术相结合的产物,具有分辨率高、体积小、简单方便等优点。将新兴的激光雷达技术与业已成熟的被动红外探测技术相结合,综合利用红外技术优秀的目标方位、俯仰参数测量能力以及激光雷达精确的距离测量能力,可以更加准确测量可疑飞行器的飞行方向、距离和速度参数[13],未来可以应用于大气层外拦截导弹动能拦截器。

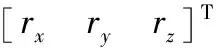
(7)

2 制导律辨识问题的可观性分析

非线性系统的可观性比线性系统复杂得多。文献[10]利用微分几何方法研究了非线性系统的局部弱能观性。

已知非线性系统为

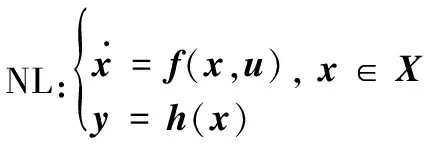
这里假设X是连通的n维C∞流形。F表示由f(x,u*)(u*是任意常数)生成的最小对合分布。h=[h1,…,hr]T,hi都是C∞类的。H是包含h1,…,hr且关于F的微分不变的最小函数空间,dH是它在X上的余分布,dH关于F也是不变的。

定义1[9]对于x0,当x1≠x0时,总有u(t)和T>0,使得在0≤t≤T时,y(t,x0,u(t))≠y(t,x1,u(t)),则称系统在x0处是可观的。如果对于一切x∈X都成立,则称系统是可观的。

定义2[9]存在x0的邻域U,任给x0的邻域V⊂U,当x1∈V,x1≠x0时,总有u(t)和T>0,使得在0≤t≤T时,x(t,x0,u(t))⊂V,x(t,x1,u(t))⊂V,且y(t,x0,u(t))≠y(t,x1,u(t)),则称系统在x0处是局部弱可观的。如果对于一切x∈X都成立,则称系统是局部弱可观的。

已知x0∈X,如果dim dH(x0)=n,那么系统在x0处是局部弱可观的。如果对于一切x∈X都成立,那么系统是局部弱可观的[9]。

将系统(1)写成一般形式

(8)

没有外部输入,所以易得

F=span{f(x)}

(9)

定义导数为

记

则

h01(x)=rx

h02(x)=ry

h03(x)=rz

h11(x)=Lf(x)h01(x)=Lf(x)rx=vx

h12(x)=Lf(x)h02(x)=Lf(x)ry=vy

h13(x)=Lf(x)h03(x)=Lf(x)rz=vz

h21(x)=Lf(x)h11(x)=Lf(x)vx=axt-axm

h22(x)=Lf(x)h12(x)=Lf(x)vy=ayt-aym

h23(x)=Lf(x)h13(x)=Lf(x)vz=azt-azm

h31(x)=Lf(x)h21(x)=-(uxm-axm)/τ

h32(x)=Lf(x)h22(x)=-(uym-aym)/τ

h33(x)=Lf(x)h23(x)=-(uzm-azm)/τ

⋮

h10,3(x)=Lf(x)h93(x)=…

H为以上向量张成的函数空间,即

H=span{rx,ry,rz,vx,vy,vz,axt-axm,axt-aym,azt-azm,

-(uxm-axm)/τ,-(uym-aym)/τ,-(uzm-azm)/τ,…}

将以上各项分别对各状态变量求偏导,生成的函数空间即为dH。将函数空间的维度改写成矩阵的秩,因此局部弱可观条件变成

(10)

式中,∂um/∂r是控制量um对于相对距离的偏导数矩阵;∂um/∂v是控制量um对于相对速度的偏导数矩阵;∂um/∂Ny、∂um/∂Nz是控制量um对于导航比Ny、Nz的偏导数。

仿照线性系统可观性理论,可以把式(10)中的矩阵看作非线性系统的可观性矩阵。

如果∂um/∂N≠0,那么就可以得到可观性矩阵满秩,系统可观。在这里忽略坐标系偏差,近似认为在比例导引律中

(11)

因而

(12)

(13)

不满秩。

这一点结合实际情景也很容易说明。控制指令为0就相当于制导律没有起作用,自然无法观测制导系数。

3 滤波器设计

设系统的非线性模型为

(14)

式中,X(t)是系统的状态变量;Z(t)是测量量;W(t)是干扰;V(t)是测量噪声。

根据泰勒公式,有

(15)

忽略二次项以后,系统可离散为

(16)

式中,F(X(k))是f(X(k))的Jacobi矩阵。

因此对应的EKF算法为

(17)

其中

(18)

(19)

Q是状态转移预测过程中的处理噪声协方差矩阵。制导律解耦对x轴方向造成的误差更大,故令vx、ax的分量大一些。为使制导系数收敛得更快,令Ny、Nz的分量大一些,令Q=diag(10,10,10,50,10,10,50,10,10,1,1),R是观测值噪声的协方差矩阵。这里测量标准差设为3 m,故取R=diag(9,9,9)。

4 弹道预报

4.1 预处理

通过卡尔曼滤波获得的估计值往往带有一定的误差,测量误差的影响会使得估计结果出现抖动的现象,如果直接用滤波器获得的结果进行预报,必然会带来很大误差,因此有必要将滤波结果进行必要的平滑处理。

(20)

由于滤波器初值选取存在误差,滤波结果收敛到真值需要一定时间。因此需要结果收敛的指标,当滤波数据达到要求后,便可利用数据进行弹道预报工作。

对于滤波产生的若干个数据x1,x2,…,从第i个数据xi开始,顺次选取N个数据,给定波动上界ε,若这N个数据中的最大值xmax和最小值xmin满足xmax-xmin<ε,则认为数据收敛,用xi+N-1进行计算;否则,从i+1开始重新选取数据。

4.2 预报方程

通过滤波获得对方制导律参数和位置速度信息后,便可通过求解微分方程进行弹道预报。

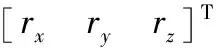
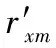
5 仿真

5.1 制导律辨识

以雷达对相对位置和相对速度的测量值作为滤波器的初值,有一定的误差,根据误差的大小设定滤波器的参数P。敌方加速度初值可取0,制导系数根据经验可取2。导弹动态特性的时间常数τ可以根据经验选取,这里取0.015,实际上,这个值对仿真结果影响很小。敌方导弹可以按照比例导引律顺利拦截我方飞行器。惯性系下相遇过程双方弹道如图2所示。

图2 相遇过程双方弹道Fig.2 Trajectories of Engagement

相对距离、相对速度、拦截导弹加速度的真实值和滤波器估计值如图3～图5所示。其中,图5还描述了拦截导弹的机动情况。

图3 相对距离的真实值和估计值Fig.3 Estimate and actual range

由图3～图5可知,通过调整滤波器的各项参数,滤波器对各项参数的估计效果均能满足要求。由于测量误差的存在,对加速度的估计结果抖动现象会比较明显。

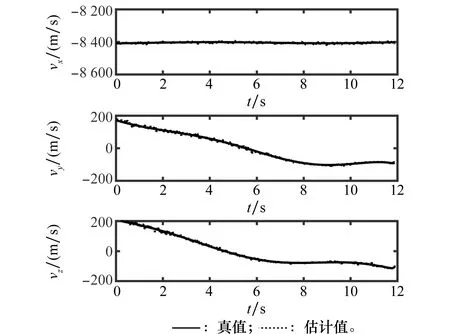
图4 相对速度的真实值和估计值Fig.4 Estimate and actual range rate

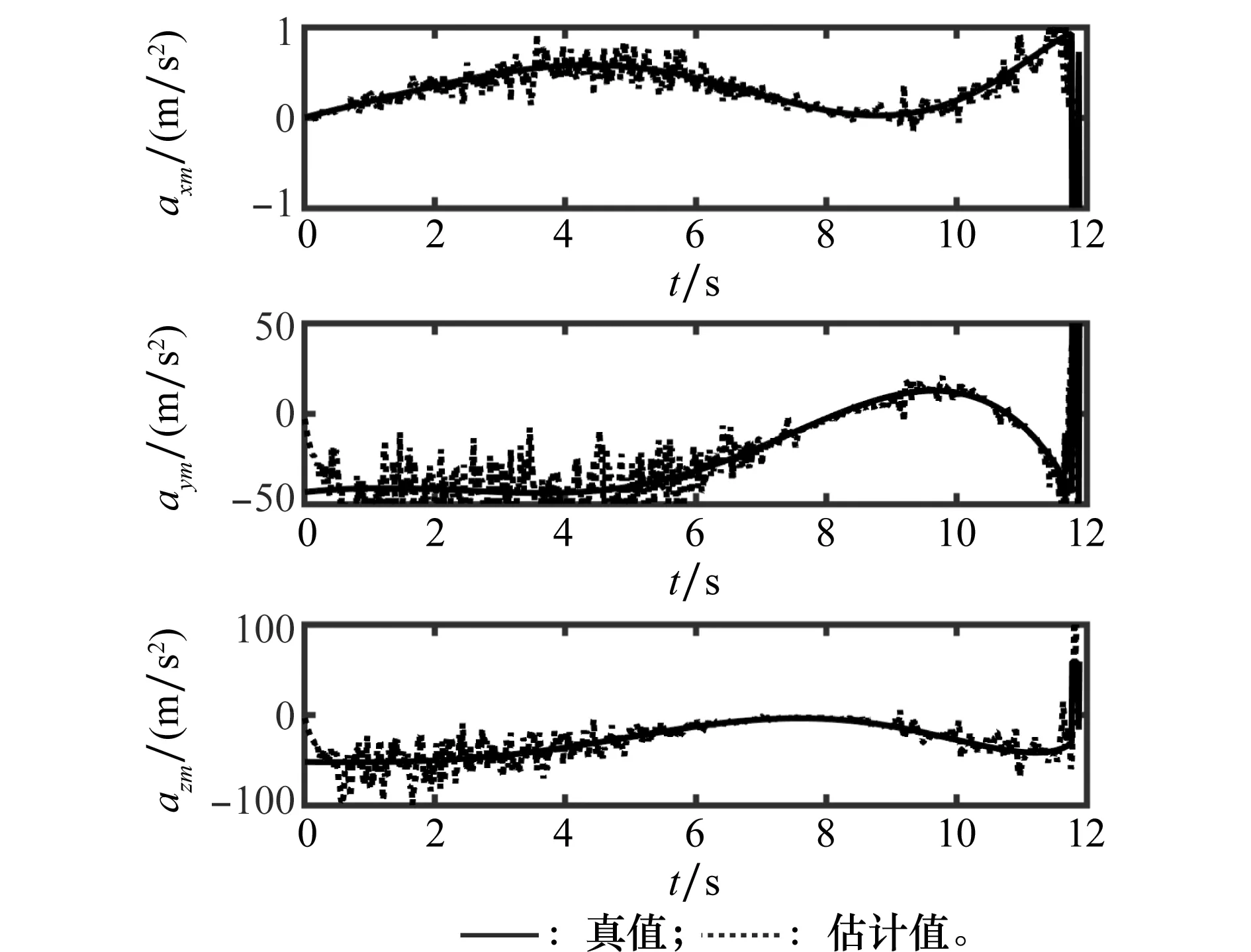
图5 拦截导弹加速度的真实值和估计值Fig.5 Estimate and actual interceptor acceleration

制导系数估计值随时间的变化情况，如图6所示。

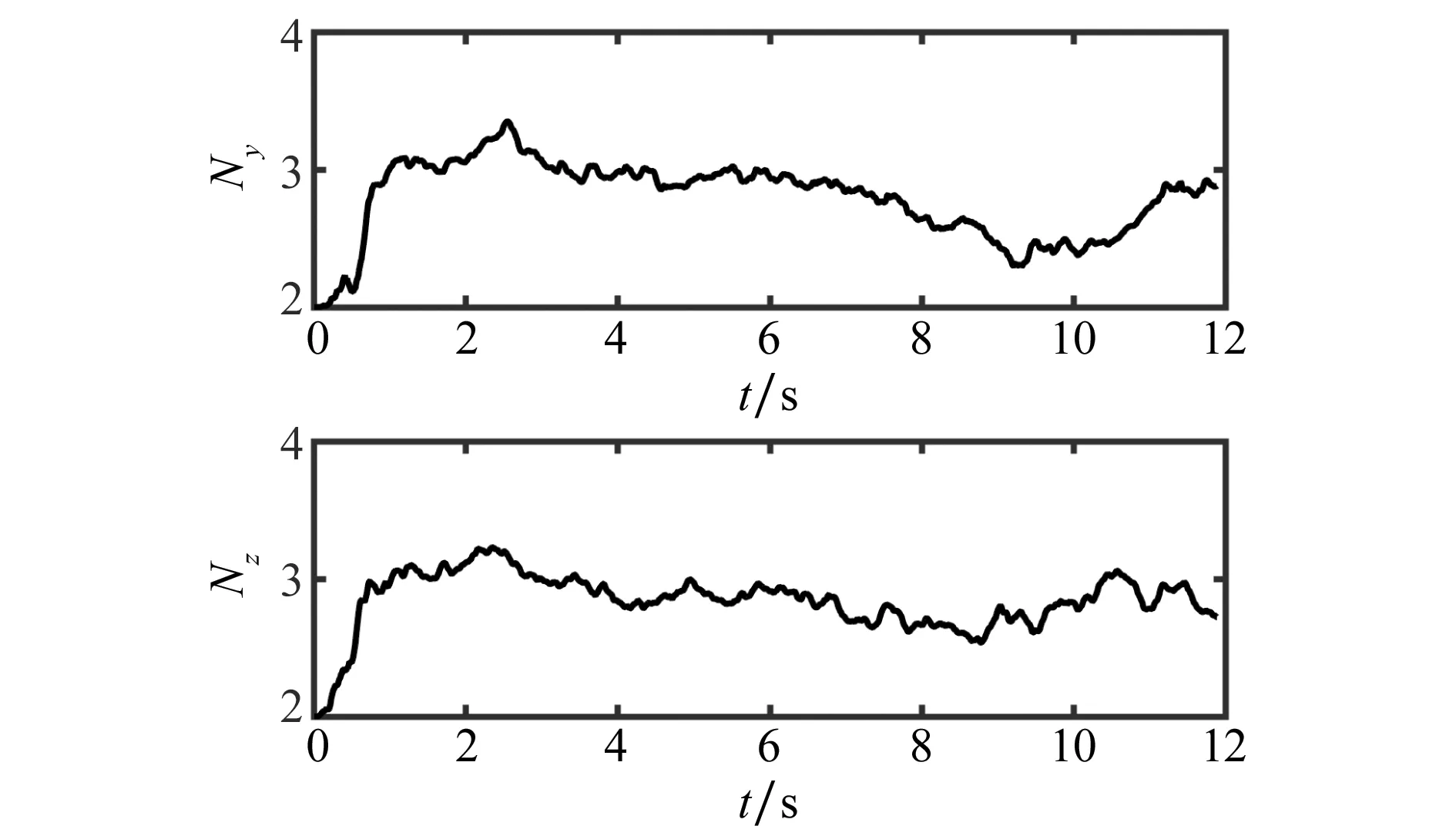
图6 制导系数估计值Fig.6 Estimate guidance coefficient

由图6可知,通过调整滤波器参数,制导系数的估计效果可以满足要求。经过平滑处理后,滤波结果可以在1 s左右到达真值附近。

5.2 弹道预报

根据前面所述方法对滤波所得数据进行处理。取M=200,N=30,ε=0.1。处理之后系统认为在1.36 s时数据可以用来预报。拦截导弹弹道预报的误差[exeyez]T如图7所示。未来10 s后,即11.36 s时的位置预报结果误差为[-2.861 0.515 -0.179]Tm,算法平均所用时间为0.045 599 s。

图7 弹道预报误差Fig.7 Error of trajectory prediction

在敌方导弹的运动过程中,x轴加速度不大,近似于匀速运动。所以初始速度一旦出现偏差,它的影响就会一直存在。而y轴和z轴,因为预报模型中有制导律的作用,所以即使初值有误差,预报位置也会有向拦截目标位置接近的趋势。这使得即使中间过程误差比较大,最终的拦截点也会和真值比较接近。而制导律中的参数,即制导系数,与真值越接近,整条预报弹道与真值也就越接近。由此可见,预报初值的精度和制导律参数辨识的精度对最后弹道预报的精度影响较大。

6 结 论

以上理论分析和仿真实验说明,在视线角速率不为0的条件下,通过EKF方法可以估计比例导引律的制导系数,收敛速度和最终精度都能满足要求。以滤波器的估计结果为预报初值,进一步可以对拦截导弹未来的位置进行预报,满足一定的精度和速度要求,对我方飞行器规避敌方的拦截具有一定意义。

[1] GROVES G W, BLAIR W D, HOFFMAN S. Some concepts for trajectory prediction for ship self defense[C]∥Proc.of the American Control Conference, 1995: 4121-4126.

[2] LIN C S, RAETH P G. Prediction of missile trajectory[C]∥Proc.of the IEEE International Conference on Intelligent Systems for the 21st Century: Systems, Man and Cybernetics, 1995: 2558-2563.

[3] 鲜勇, 田海鹏, 王剑, 等. 中段智能突防的EKV导引律辨识方法研究[J]. 弹箭与制导学报, 2013, 33(6): 1-5.

XIAN Y, TIAN H P, WANG J, et al. Method of the identification of the EKV guidance law based on the middle intelligent penetration[J]. Journal of Projectiles Rockets Missiles & Guidance, 2013, 33(6): 1-5.

[4] NAIDU V P S, GIRIJA G, SHANTHAKUMAR N. Three model IMM-EKF for tracking targets executing evasive maneuvers[C]∥Proc.of the 45th AIAA Aerospace Sciences Meeting and Exhibit, 2007: AIAA-2007-1204.

[5] SHAFERMAN V, SHIMA T. Cooperative multiple-model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance Control and Dynamics, 2010, 33(6): 1801-1813.

[6] 王小平, 蔡远利, 于振华, 等. 一种导弹导引律及参数的非线性 MMAE 辨识方法[J]. 飞行力学, 2015 (5): 430-434.

WANG X P, CAI Y L, YU Z H, et al. Nonlinear MMAE-based missile guidance law and parameter identification[J]. Flight Dynamics, 2015 (5): 430-434.

[7] DIONNE D, MICHALSKA H. Decision-directed adaptive estimation and guidance for an interception endgame[J]. Journal of Guidance Control and Dynamics, 2006, 29(4): 970-980.

[8] CHEN R H, SPEYERY J L. Homing missile guidance and estimation for three-dimensional intercept[C]∥Proc.of the AIAA Guidance Navigation and Control Conference and Exhibit, 2008: AIAA-2008-7457.

[9] 韩正之,潘丹杰,张钟俊.非线性系统的能观性和状态观测器[J].控制理论与应用,1990,7(4): 1-9.

HAN Z Z, PAN D J, ZHANG Z J. Nonlinear observability and state observers[J].Control Theory and Applications,1990,7(4):1-9.

[10] HERMANN R, KRENER A J. Nonlinear controllability and observability[J]. IEEE Trans.on Automatic Control, 1977, 22(5): 728-740.

[11] 慈颖. 高精度实时弹道预报方法研究[J]. 飞行器测控学报, 2010(5): 80-84.

CI Y. Study on algorithm for high accuracy real-time trajectory prediction[J]. Journal of Spacecraft TT&C Technology, 2010(5): 80-84.

[12] 陈映, 文树梁, 程臻. 一种基于多模型算法的纯弹道式弹道落点预报方法[J]. 宇航学报, 2010, 31(7): 1825-1831.

CHEN Y, WEN S L, CHENG Z. An IMM-based impact point prediction method of ballistic target[J]. Journal of Astronautics, 2010, 31(7): 1825-1831.

[13] 刘斌, 张军, 鲁敏, 等. 激光雷达应用技术研究进展[J]. 激光与红外, 2015, 45(2): 117-122.

LIU B, ZHANG J, LU M, et al. Research progress of laser radar applications[J].Laser & Infrared,2015,45(2):117-122.