基于知识辅助的天波雷达海杂波抑制方法
曹 健, 王兆祎, 胡进峰, 何子述
(电子科技大学电子工程学院, 四川 成都 611731)
0 引 言
天波雷达中,舰船等慢速目标回波的多普勒谱靠近强大的海杂波谱,容易被海杂波所掩盖[1]。因此,抑制海杂波是检测慢速舰船目标的关键问题之一,受到广泛关注。
目前,已有的海杂波抑制方法主要分为3类:①基于海杂波信号重建和对消的方法,如循环对消方法[2]、基于幅度相位估计的对消方法[3]以及神经网络方法[4],这类方法首先估计并重构海杂波信号,然后从原信号中减去重构的海杂波信号;②子空间类方法,如基于特征值分解的方法[5]、基于奇异值分解的方法[6]和通过多普勒频率估计杂波子空间的方法[7],这类方法根据杂波在子空间的聚集特性,将杂波空间分为强杂波空间和噪声子空间,通过将回波信号投影到噪声子空间来实现海杂波抑制;③基于最优滤波的方法[8-9],这类方法在目标无失真通过滤波器的约束条件下,最小化输出能量,实现海杂波的抑制。
其中,第3类基于最优滤波的方法尤其受到关注。该方法将海杂波抑制问题转换成最优化问题,直接将最大化输出信杂噪比作为优化的目标函数,因此理论上,在所有滤波器中,该方法输出信杂噪比最大,效果最好。文献[8]利用目标信号的单频特性,以最大化目标位置的输出信杂噪比为优化的目标函数,提出利用最优滤波抑制海杂波方法。文献[9]将最优滤波方法与神经网络方法进行对比,发现最优滤波方法具有更大的输出信杂噪比,进一步证明了在复杂的海态环境下,最优滤波方法比神经网络方法具有更好的海杂波抑制效果。
但是,上述方法中都没有有效利用先验知识进行杂波抑制。在目前已有的利用先验知识杂波抑制方案中,主要针对机载雷达方向[10-11]和基于知识空时自适应处理(space-time adaptive processor,STAP)算法方向[12-14],在天波雷达海杂波抑制领域很少有方法考虑到利用先验知识提升海杂波抑制性能,同时也没有考虑到进行海杂波抑制时,利用海面环境因素作为先验知识提升海杂波抑制效果。
在天波雷达中,除了脉冲重复周期、天线增益等雷达参数等先验知识,还有海平面风速、风向等环境先验知识,将这些知识加入最优滤波器的设计,有望提升海杂波的抑制效果。因此,本文提出基于知识的天波雷达海杂波抑制方法。该方法首先利用脉冲重复周期、海平面风速、风向等作为先验知识构建杂波模型,然后将杂波的先验模型加入最优滤波设计中,得到新的基于知识的海杂波抑制算法。对实测数据的处理结果表明,与文献[8-9]的最优滤波类方法相比,本文所提方法海杂波抑制效果可提升3 dB以上。
1 最优滤波海杂波抑制方法
本文采用相控阵天波超视距雷达,其发射信号为线性调频连续波,接收信号在经过匹配滤波和多普勒处理后可得到距离-多普勒数据矩阵,该矩阵中距离单元l处的回波信号r(l)∈CM×1可以表示为
r(l)=x(l)+c(l)+n(l)
(1)
式中,x(l),c(l),n(l)分别为距离单元l(l=1,2,…,L)处的目标、杂波和噪声;M为相干积累时间(coherent integration time,CIT)内的脉冲数目。
距离单元l中的第i个多普勒单元的时域导向向量为s(fi)∈CM×1,表达式为
(2)
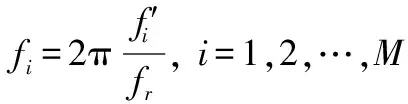
文献[8-9]给出的未利用知识辅助的最优滤波海杂波抑制方法为:在距离单元l第i个待检测多普勒单元处,以目标信号无失真通过滤波器为约束条件,令滤波后的信号能量最小,从而实现海杂波的抑制。
(3)
式中,H表示共轭转置;wo为待计算得到的最优滤波器权向量;Rr为利用参考单元估计得到的距离单元l处的杂波协方差矩阵,即
(4)
式中,L为总的距离单元数;r(l)为距离单元l处的回波信号;CUT表示待检测单元。
2 基于知识辅助的天波雷达海杂波抑制方法
针对目前的天波雷达海杂波抑制方法中没有有效利用先验知识的问题,本文提出将天波雷达的先验知识结合到海杂波抑制算法中,以提高海杂波抑制效果。
所提方法首先根据天波雷达的先验知识对天波雷达海杂波建模,所用到的天波雷达先验知识主要有:脉冲重复周期、雷达工作频率、海面风速、风向(通过气象雷达测得)。在此基础上,将海杂波模型与传统的基于最优滤波的天波雷达海杂波抑制方法结合,得到新的基于知识的天波雷达海杂波抑制方法,本文所提方法的计算流程图如图1所示。
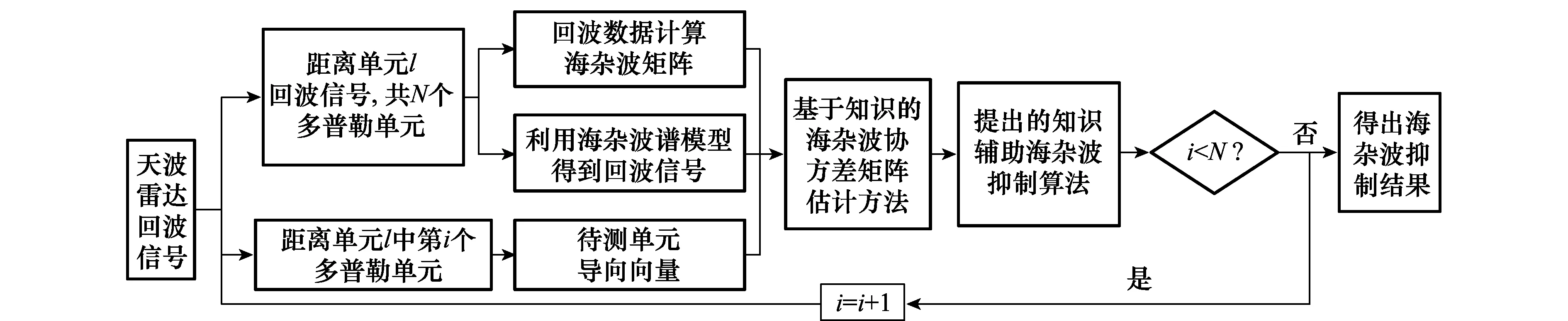
图1 基于知识辅助的海杂波抑制算法流程图Fig.1 Knowledge-aided ocean clutter suppression algorithm flow chart
2.1 基于知识的天波雷达谱模型
2.1.1 海杂波回波谱
天波雷达探测范围中大部分区域为海面区域,在天波雷达接收的信号中,海杂波信号强度远大于其他信号。通过文献[15-17]中海杂波谱分析可知,海杂波谱主要由一阶海杂波谱和二阶海杂波谱组成。
σ(w)=σ(1)(w)+σ(2)(w)
(5)
式中,w为多普勒频移;σ(1)(w),σ(2)(w)分别表示海杂波的一阶谱和二阶谱。
2.1.2 海浪的有向高谱
有向谱用于描述海浪波高随海浪频率和传播方向的分布情况,可以表示为无向波高谱和方向因子的乘积。
S(k)=S(k)d(θk-β)
(6)
式中,S(k)代表无向波高谱,用于描述波高相对于频率的分布,在天波雷达工作的高频区域内,由观测资料综合得到其表达式为
S(k)=0.005k-4exp[-0.74(kc/k)2]
(7)
式中,kc=g/v2为无向浪高谱的截止波数,v为海面上19.5 m处的风速。
d(θk-β)代表方向因子,其表达式为
(8)
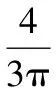
2.1.3 海杂波一阶谱
海杂波一阶谱的强度很大,谱宽较窄,Barrick将高频雷达海面回波多普勒频谱和海面的浪高谱、海面表面流速度以及海面风速参数相联系,在无表面流的情况下,导出单位面积海面的一阶散射强度为
(9)
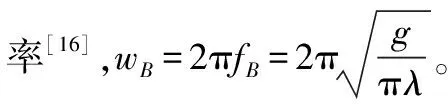
2.1.4 海杂波二阶谱
高阶海杂波谱不仅存在幅度较大的一阶谱,在一阶布拉格峰周围存在低十几分贝的连续谱,即海杂波的二阶谱。Barrick推导出窄波束雷达二阶回波的多普勒截面方程[17]为
(10)
式中,Γ是耦合系数,包含水动力学耦合系数ΓH和电磁学耦合系数ΓEM两部分
Γ=ΓH+ΓEM
(11)
(12)
(13)
Δ是垂直极化电波入射粗糙海面时的归一化波阻抗,近似为:Δ=0.11-0.012i;k0为雷达波矢量;k是第一列正弦波的波矢量;k′是第二列正弦波的波矢量。对电磁耦合项,k,k′还需要满足
k·k′=0
(14)
即两列波矢量相互正交,否则ΓEM=0。
通常来说,二阶谱存在的频谱范围为1.1fB<|f|<2fB,0<|f|<0.9fB,但是在实际情况中,针对舰船检测的多普勒观测范围通常大于-2fB~2fB,所以在模拟海杂波谱时需要计算更大范围的杂波谱,通过补零来实现,由此可以得到海杂波二阶谱。
2.2 基于知识的海杂波协方差估计方法
在问题描述中给出了在距离-多普勒数据矩阵中,利用参考单元得到的距离单元l处的杂波协方差矩阵见式(4)。
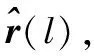
(15)
将式(4)表示的基于接收信号的杂波协方差矩阵和式(15)表示的基于谱模型的杂波协方差矩阵进行有效结合,可以估计出基于知识的海杂波协方差矩阵为
Rk=αRr+βRC
(16)
式中,α,β为权值系数,用于调节估计的海杂波协方差矩阵中Rr,RC的相对大小。
α,β系数取值的目标为:使得在距离单元l第i个待检测多普勒单元中,估计的基于知识的海杂波协方差矩阵Rk=αRr+βRC能够最佳地拟合无目标存在时的真实海杂波的协方差矩阵,由此提出α,β系数计算方案为[18]
(17)
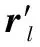
2.3 基于知识辅助的海杂波抑制方法
利用基于知识的海杂波协方差矩阵Rk,提出基于知识辅助的海杂波抑制方法,即
(18)
式中,wk为待计算得到的距离单元l中第i个多普勒单元处的基于知识的最优滤波器权向量;Rk由式(16)得到;α,β由式(17)得到。
传统最优滤波方法中,选择相邻距离单元作为参考单元是基于相邻距离单元的杂波环境与待测单元杂波环境相同的假设,但是在实际情况中,由于海杂波是很不稳定的信道环境,实测海杂波受海况、风向等环境因素的影响很大,相邻两个距离单元的杂波环境可能区别很大,此时,利用相邻距离单元得到的杂波协方差矩阵的误差很大,传统的最优滤波方法得到的海杂波抑制效果会明显下降。
在本文基于先验知识的海杂波抑制方法中,利用已知的脉冲重复周期、雷达工作频率等雷达参数以及海平面风向、风速等环境因素作为先验知识,构造基于先验知识的杂波协方差矩阵,利用权值系数调节两个协方差矩阵的相对大小,可以很好解决不稳定环境下相邻单元突变造成的协方差矩阵不准确的问题,提升海杂波的抑制效果。
利用拉格朗日乘子法对式(18)处理得到距离单元l处的第i个待检测多普勒单元处的基于知识的最优滤波器权向量为
(19)
距离单元l处的第i个待检测多普勒单元的输出信杂噪比(signal to clutter plus noise rate,SCNR)为
(20)
3 仿真结果
仿真全部采用某天波雷达的实测数据,对实测数据的处理表明,与文献[8-9]中的方法相比,所提方法对海杂波的抑制性能可提升2~4 dB。
所用数据为某天波超视距雷达实测数据,数据采集参数为:雷达工作频率f0=18.3 MHz,脉冲重复周期T=12 ms,脉冲积累个数M=512,相干积累时间CIT=6.144 s。由观测雷达得到的参数为:雷达波束与风向之间夹角为152°,雷达波到海浪波的入射角为21°,海平面19.5 m处的风速为4级风速,约17 m/s。
为了便于与文献[8-9]中最优滤波方法对比分析,参考单元数目、处理场景和结果显示都参照文献[8-9]的形式。
3.1 实测海杂波抑制
为了验证所提算法的有效性,对一组实测数据进行处理和对比分析。其中,该组数据中有一个已知目标,其多普勒频率为4.72 Hz。
某距离单元的原始信号频谱图如图2所示。该距离单元中有一个已知的舰船目标,该目标在4.72 Hz处。从图2中可看出,目标信号处在强的海杂波谱中,难以检测,因此需要进行海杂波抑制。
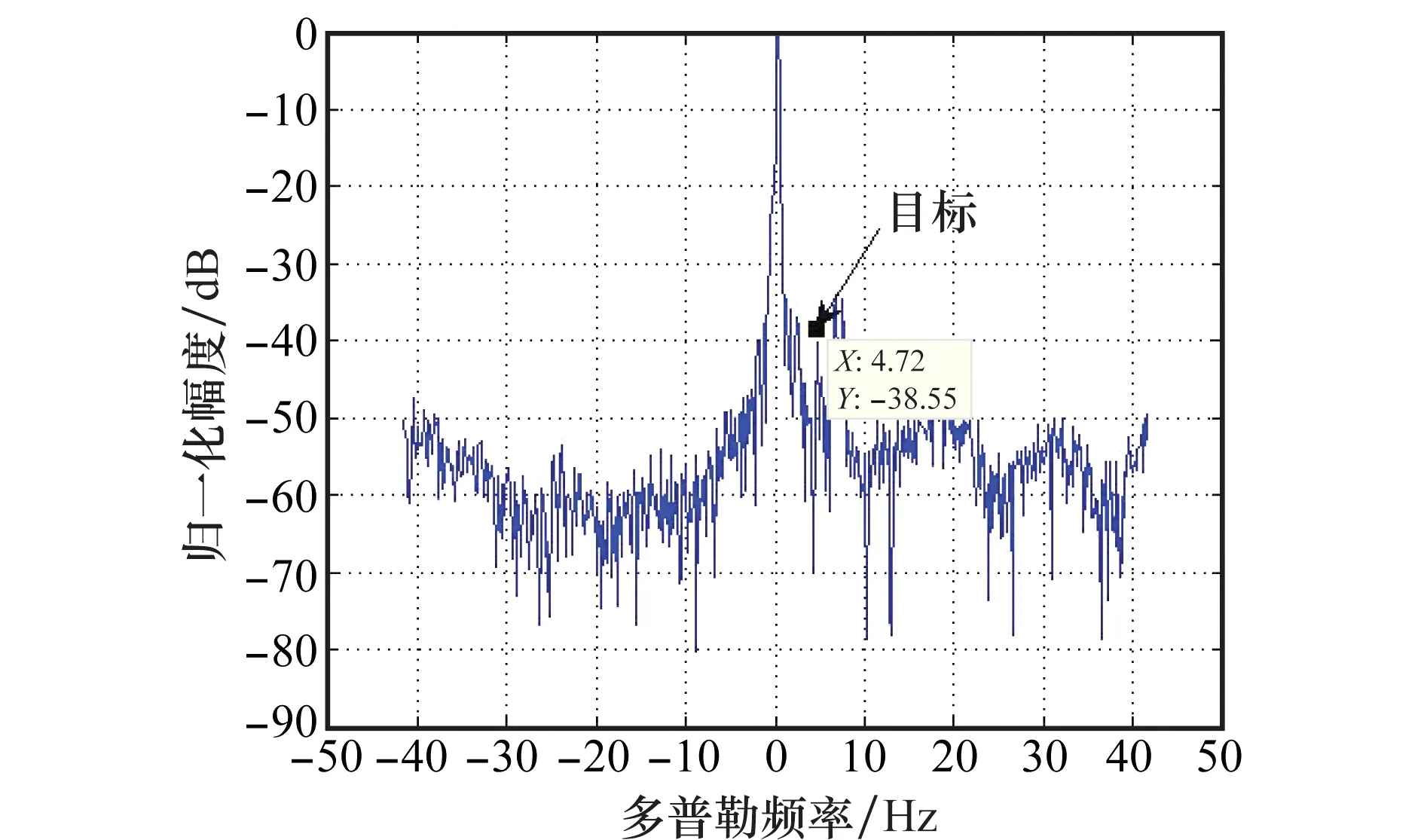
图2 某距离单元信号频谱Fig.2 Signal spectrum of one distance cell
图3为该距离单元的归一化输出信杂噪比。其中,图3(a)为最优滤波海杂波抑制方法的结果;图3(b)为基于先验知识的海杂波抑制方法的结果。
从图3(a)中可以看出,利用最优滤波海杂波抑制方法得到的最大残留海杂波在16.44 Hz处,其SCNR为-5.433 dB;从图3(b)中可以看出,利用本文提出的海杂波抑制方法得到的最大残留海杂波在2.604 Hz处,其SCNR为-8.433 dB。因此,图3的仿真结果表明,本文提出的基于知识辅助的海杂波抑制方法相比于最优滤波方法提升了3 dB。
3.2 性能对比分析
本实验验证了在不同输入SCNR的条件下,最优滤波方法和本文所提方法抑制海杂波的性能对比分析。仿真结果表明,所提方法比最优滤波方法对海杂波的抑制性能提升3 dB左右。
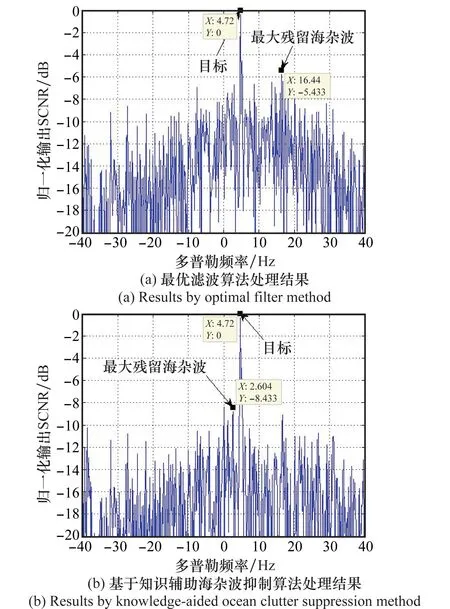
图3 该距离单元中归一化输出信杂噪比Fig.3 Output SCNR of this distance cell
实验用实测的天波雷达海杂波数据。为了便于性能分析,在第144个距离单元添加多普勒频率为fd=1 Hz的目标,目标信号的输入SCNR从-25~-10 dB变化。
海杂波抑制的性能曲线如图4所示,表明了在不同输入SCNR条件下,目标位置SCNR与抑制后最强残留海杂波SCNR的差值。该差值表征了目标对应多普勒单元处的输出 SCNR 的凸起程度,差值越大说明目标越容易被检测到。
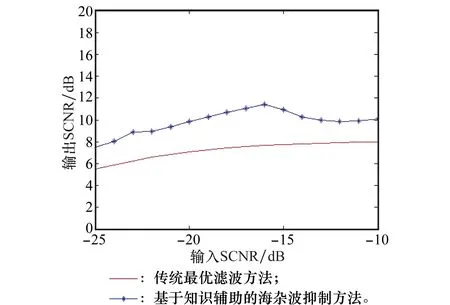
图4 海杂波抑制的性能曲线Fig.4 Performance curve of ocean clutter suppression
从图4中可以看出,利用基于先验知识的海杂波抑制方法比最优滤波海杂波抑制方法提升2~4 dB。
4 结 论
针对目前天波雷达海杂波抑制方法中未充分利用先验知识的问题,提出基于先验知识的海杂波抑制方法,经过实测数据验证得出,基于先验知识的天波雷达海杂波抑制方法相比于最优滤波海杂波抑制方法,性能提升3 dB左右。
[1] HEADRICK J M, SKOLNIK M I. Over-the-horizon radar in the HF band[J]. Proceedings of the IEEE, 1974, 62(6):664-673.
[2] ROOT B T. HF-over-the-horizon radar ship detection with short dwells using clutter cancelation[J].Radio Science,2016,33(4): 1095-1111.
[3] GUO X. The ship detection of sky wave over-the-horizon radar with short coherent integration time[J]. Journal of Electronics & Information Technology, 2004, 26(4): 613-618.
[4] XUE Y, YANG L, HAYKIN S. Decoupled echo state networks with lateral inhibition[J]. Neural Networks, 2007, 20(3):365-376.
[5] WANG G, XIA X G, ROOT B T, et al. Manoeuvring target detection in over-the-horizon radar using adaptive clutter rejection and adaptive chirplet transform[J].IEE Proceedings Radar, Sonar and Navigation, 2003, 150(4):292-298.
[6] TANG Y, LUO X, YANG Z. Ocean clutter suppression using one-class SVM[C]∥Proc.of the IEEE Signal Processing Society Workshop on Machine Learning for Signal Processing, 2005:559-568.
[7] ZHAO Z, CHEN J, ZHENG B. A method to estimate subspace via Doppler for ocean clutter suppression in skywave radars[C]∥Proc.of the IEEE CIE International Conference on Radar, 2011:145-148.
[8] WU P, WANG J, WANG W. A novel method of small target detection in sea clutter[J]. Isrn Signal Processing, 2014, 2011(2011).
[9] HU J, ZHU H, LI H, et al. Sea clutter suppression and weak target signal enhancement using an optimal filter[J]. IEICE Trans.on Fundamentals of Electronics Communications & Computer Sciences, 2016, 99(1):433-436.
[10] 周宇, 张林让, 刘楠, 等.空时自适应处理中基于知识的训练样本选择策略[J].系统工程与电子技术, 2010,32(2):405-409.
ZHOU Y, ZHANG L R, LIU N, et al. Knowledge aided secondary data selection in space time adaptive processing[J]. Systems Engineering and Electronics, 2010, 32(2):405-409.
[11] CAPRARO C T, CAPRARO G T, BRADARIC I,et al. Implementing digital terrain data in knowledge aided space-time adaptive processing[J]. IEEE Trans.on Aerospace and Electronic Systems, 2006, 42(3):1080-1099.
[12] 陆达, 张弓.知识辅助的机载MIMO雷达降秩STAP算法[J].数据采集与处理, 2012,27(4):429-435.
LU D, ZHANG G. Knowledge-aided reduced-rank STAP algorithm for airborne MIMO radar[J]. Journal of Data Acquisition & Processing, 2012, 27(4):429-435.
[13] 李晓明,冯大政,夏宇垠,等.基于重构协方差矩阵空时二维杂波抑制方法[J].系统工程与电子技术,2008,30(12):2366-2370.
LI X M, FENG D Z, XIA Y Y, et al. Method for clutter suppression based on covariance matrix reconstruction in airborne radar[J]. Systems Engineering and Electronics, 2008, 30(12):2366-2370.
[14] 刘聪锋,廖桂生.基于Bayes准则的STAP协方差矩阵估计算法[J].西安电子科技大学学报(自然科学版),2008,35(2):223-227.
LIU C F, LIAO G S, Covariance matrix estimation for the STAP based on the Bayes criterion[J]. Journal of Xidian University (Science and Technology), 2008, 35(2):223-227.
[15] 文必洋, 石振华. 高频雷达海洋回波谱的数字模拟[J].武汉大学学报,2000,46(1): 127-130.
WEN I Y, SHI Z H. Numerical simulation for the sea echo spectrum of HF radar[J].Wuhan University Journal,2000,46(1):127-130.
[16] BARRICK D. First-order theory and analysis of MF/HF/VHF scatter from the sea[J]. IEEE Trans.on Antennas and Propagation, 1972, 20(1):2-10.
[17] BARRICK D. Remote sensing of sea state by radar[C]∥Proc.of the IEEE International Conference on Engineering in the Ocean Environment, 1972: 186-192.
[18] WU Y, WANG T, WU J, et al. Robust training samples selection algorithm based on spectral similarity for space-time adaptive processing in heterogeneous interference environments[J]. IET Radar, Sonar and Navigation, 2015, 9(7):778-782.

