两轮式随动支撑装置轨迹生成算法优化及编程实现

（河北科技大学 机械工程学院，石家庄 050018）

0 引言

与传统材料相比，先进复合材料[1]具有质量轻、强度高、密度低、设计制造一体化等优点，现已被大量应用于航空航天领域[2]。目前，对飞机机身、机翼、风电叶片等大型复合材料构件的加工工艺采取了纤维丝束自动铺放技术[3]。但由于飞机机身等为弱刚性构件，在铺放过程中，加工力的作用会使加工构件产生过大的挠曲变形，影响加工精度。为了减少构件在铺放过程中产生的挠性变形，满足铺放工艺要求，河北科技大学机械学院设计了一种能用于正曲率截面构件的两轮式随动支撑装置[6]，并开发了支撑轮运动轨迹自动生成软件。

1 两轮式随动支撑装置及轨迹生成算法

图1 两轮式随动支撑装置

图2 工作原理图

两轮式随动支撑随动装置如图1所示，主要有伺服电机、丝杠螺母副、直线滚动导轨、支撑轮及安装底座等部分构成。该装置的工作原理如图2所示，工件在设备主轴的带动下绕工件旋转中心O做逆时针回转运动时，半径为R的左右两支撑轮在距工件旋转中心为L的支撑轮运动水平线上水平往复运动，其瞬态位置由上位计算机提前计算生成，并传送给下位的运动控制器，运动控制器根据主轴旋转角度，通过控制两套伺服电机丝杠系统来分别控制两个支撑轮的瞬态位置，使其始终与工件相切，对工件进行实时支撑[3]。

图3 求解O'iωi示例图

如图3所示，以右支撑轮为例，轨迹生成算法步骤如下。被支撑截面轮廓曲线以多线段形式存储，多线段的各端点按顺时针依次用Pi（xi,yi），支撑位置取在各多段线的中点Mi（xMi,yMi）（其中i=1,2,3,…），过点Mi做线段PiPi+1的中垂线，设中垂线上距离点Mi为R（支撑轮半径）的点为线段PiPi+1与线段垂直，故线段的斜率为：

此时有限制条件yOi'＜yMi。根据式(1)、式(2)求解得到坐标为然后将支撑轮与芯模以O为圆心，为半径逆时针旋转，直到支撑轮圆心位于直线y=-L上，此时为支撑轮在该处的支撑位置Oi(xoi，yoi)，所以|OO'i|=|OOi|。则：

2 支撑轨迹生成算法的优化改进

2.1 求解O'i的算法改进

联立式(1)和式(2)两式可得：

将式(2)代入式(1)可求得：

将式(4)代入式(1)可求得：

以上两组解分别分布在被支撑截面轮廓的内、外两侧。由于支撑轮圆心位于轮廓外才是合理的，所以应取距离旋转中心O较大的值作为的坐标值。

上述求解过程中，斜率不存在的情况可能发生，也就是相邻的两坐标点的横坐标值相等。当斜率不存在时，用下面算法求解的坐标值。

当xMi＞0时，坐标点位于第一、四象限时：yO'I=yMi，xO'I=yMi+R；

当xMi＜0时，坐标点位于第二、三象限时：yO'I=yMi，xO'i=yMi-R。

2.2 求解芯模旋转角ω的算法改进

图4 旋转角度为钝角

如图4所示该直线的初始位置在第一象限，旋转至支撑位置的角度为此时角度ω为钝角。对上述问题在编程过程中加入了二维坐标旋转公式，假设上一次的旋转角为旋转之前O'i的坐标为(xO'i，yO'i)，旋转后的点记为Or(xOr，yOr)，那么：

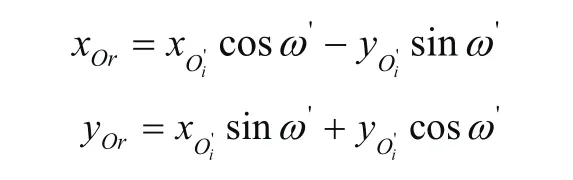
被支撑截面每旋转一次，对所有轮廓点的坐标在二维坐标系中进行相旋转角度的坐标变换。这样就保证了每次旋转时两直线之间的夹角都为锐角，那么原算法中求取旋转角的方法就适用于各象限区域点。

3 支撑轮运动轨迹编程实现及仿真

针对上述两轮式支撑随动装置，根据算法流程图，采用VB6.0对算法进行了编程实现，下面对实现过程中的关键步骤做详细阐述。

3.1 读取支撑截面DXF文件

截取被支撑构件在支撑位置处的截面轮廓信息，采用AutoCAD软件将该截面轮廓转换成首尾相接的闭合多线段，保存成DXF格式的文件。

在该DXF文件中，每段信息都以“0”为开始，整个文件以“ENDSEC”为结束，所需图形几何信息全包含在ENTITIES(实体段)中。实体段存储的图元类型为LWPOLYLINE(多线段)，组码“10”后的码值为多线段上端点X轴坐标值，组码“20”后的码值为多线段上端点Y轴的坐标值[7]，如图5所示。

在VB6.0中利用LINE INPUT指令逐行读取DXF文件中文本内容，根据关键字“0”、“ENTITIES”、“LWPOLYLINE”、“10”和“20”等即可读取各多线段端点的坐标值，并按读取先后顺序保存在一个二维动态数组中。

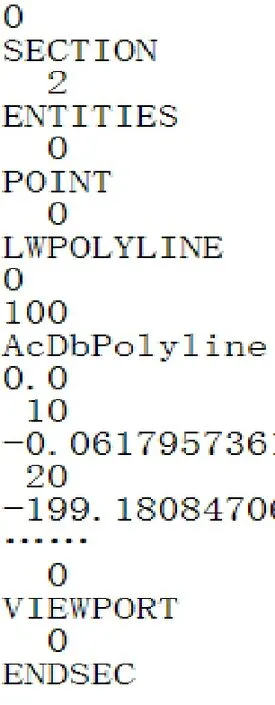
图5 DXF文件格式

图6 支撑圆截面初始仿真状态

图7 理论值计算方法

3.2 判断读取点的顺序

选择初始三个连续坐标值，分别以A(x1,y1),B(x2,y2),C(x3,y3)表示。

3.3 运动仿真功能开发

为了能直观观察计算生成的运动轨迹是否合理，开发了图形运动仿真功能。在仿真界面中，用两个圆来表示左右支撑轮，在VB6.0中采用CIRCLE指令生成。利用FOR-NEXT循环和PSET指令将从DXF文件中读取的端点坐标逐点重画，生成被支撑截面，如图6所示。

为实现被支撑截面绕旋转中心的动态旋转，每隔一定角度对被支撑截面的轮廓点做一次坐标旋转变换，再用PSET指令逐点画出旋转后的截面图形。

利用前述算法生成的支撑轮的圆心运动轨迹保存在动态数组中。仿真时，被支撑截面每旋转一定角度，从动态数组中读取该角度对应的支撑轮当前位置值，利用CIRCLE指令在新位置上重新画出支撑轮，实现支撑轮轨迹的运动仿真。

4 实验验证

为验证软件自动生成的支撑轮轨迹数据，需将其与理论值比较。实验中，采用了几何测量的方法获得被支撑截面轮廓的理论值。具体方法是在AutoCAD软件中，对芯模每隔相同角度进行一次旋转，每旋转一次在支撑轮运动水平线上做左右两个圆（代表支撑轮）与芯模相切，如图7所示。然后利用软件中的测量工具量取两支撑轮中心距旋转中心之间的距离OO左和OO右。已知OQ的距离为L，则可利用三角形勾股定理求得两支撑轮位置|OO左|和|OO右|。

选取圆截面构件、椭圆截面构件和小鹰500飞机机身芯模对软件自动生成支撑轨迹数据进行了实验验证。实验的参数为：主轴旋转中心距支撑轮运动水平线的距离为L=175mm，支撑轮的半径R=25mm。

4.1 支撑圆截面构件

两轮式支撑装置支撑圆截面构件，理论上无论圆截面随着主轴旋转角度如何，左、右两支撑轮的位置应固定不变，并且左右两支撑轮应保持对称。在验证过程中，用内接于半径为170mm的边数为720的正多边形近似代替圆。实验时，经软件自动计算生成的两支撑轮的全部轨迹位置固定不变且距支撑轮运动水平线位置Q距离为86.02mm，与理论值相符。

4.2 支撑椭圆截面构件

选取一个长轴为170mm，短轴为155mm的椭圆形截面，每隔15度测量计算一次理论值，将理论值与利用软件自动生成的轨迹数据进行对比，如表1所示。

表1 支撑椭圆截面构件实验数据（单位：mm）

分析实验数据，左支撑最大误差为0.466mm，平均误差为0.189mm；右支撑最大误差为0.293mm，平均误差为0.172mm。

4.3 支撑小鹰500机身芯模

小鹰500机身芯模截面接近四方形，截面轮廓点距旋转中心距离范围在150mm～180mm之间，在四角处曲线弯曲明显，曲率变化大，而其他线段近乎直线，曲率变化小，且整个轮廓曲线无负曲率。每隔5度测量计算一次理论值，将理论值与自动生成轨迹数据进行对比，如表2所示。

分析实验数据，左支撑最大误差为0.361mm，平均误差为0.098mm；右支撑最大误差为0.289mm，平均误差为0.078mm。

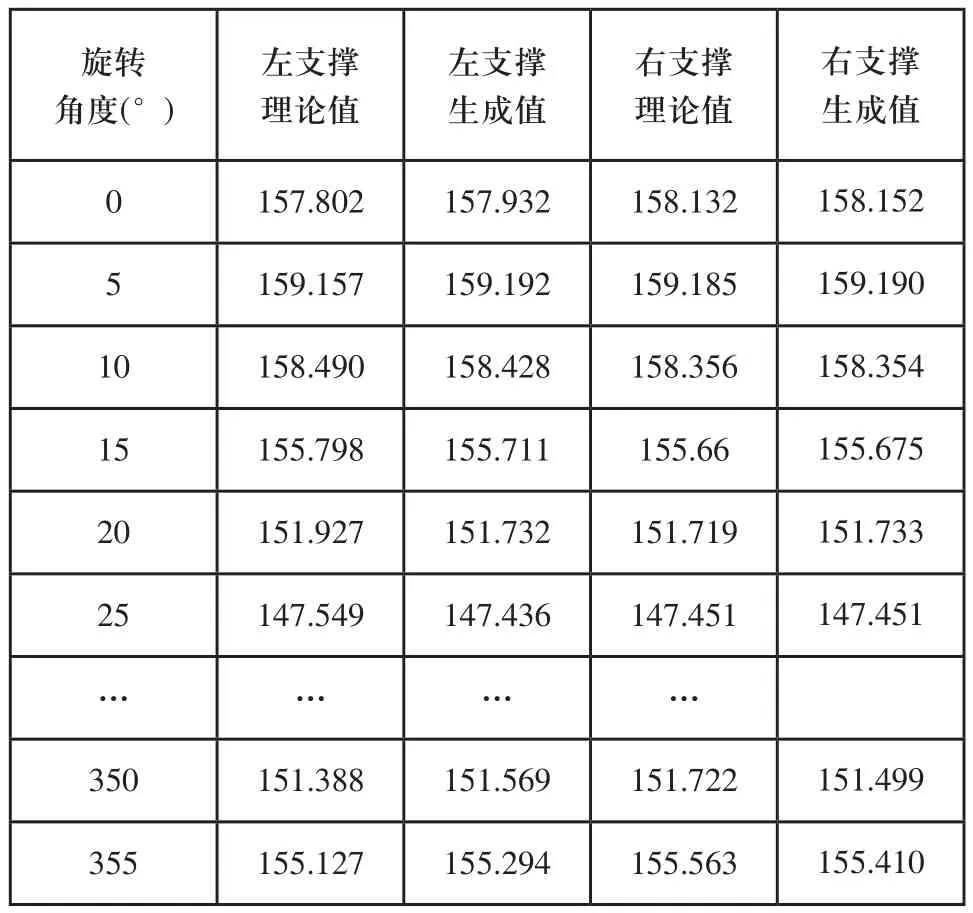
表2 支撑机身芯模截面构件实验数据（单位：mm）

4.4 误差分析

影响误差大小的因素如下：1）支撑截面的DXF文件中保存多线段时，保存的点数多少会影响误差大小，增加点数会使支撑位置更精确，有利于减小误差；2）对于曲率不同的图形，曲率变化大时存取的多线段多于曲率变化小时存取的多线段，导致取值不均匀，影响误差大小；3）支撑轮的运动轨迹是按照所存取的多线段的端点值生成的，不能保证在每隔相同的角度都有确定的支撑位置与该角度对应，编程实现时选取该角度附近的两个支撑位置取平均值来作为该角度的支撑位置，从而产生误差。

【】【】

5 结论

针对两轮式随动支撑装置开发的支撑轨迹自动生成软件，能够读取支撑构件截面的DXF文件，提取轮廓多线段信息，自动计算出两支撑轮的位置轨迹数据。经不同截面形状构件的实验验证，其数据误差大小合理，能够满足工程实际运行对误差的允许值。该软件配合下位支撑运动控制系统使得两轮式随动支撑装置的运行变得简单可靠。

[1]陈博.复合材料发展现状要略[J].高科技纤维与应用,2012,37(6):53-56.

[2]王恩青,张斌.复合材料在航空航天中的发展现状和未来展望[J].科技信息,2011,(33):290-290.

[3]许斌,安鲁陵,肖军,周来水.自动铺丝机运动控制信息的生成与仿真[J].制造业自动化,2005,27(1):1-4,73.

[4]冯磊强.复合材料异型构件铺放设备中间支撑系统研究[D].石家庄:河北科技大学,2016:7-14.

[5]辛志博.非圆截面旋转加工中间支撑系统设计[D].石家庄:河北科技大学,2014:14-16.