企业财务困境预测研究的历史演进

（博士）

一、财务困境的概念内涵

虽然许多文献将财务困境定义为“长期严重的现金流问题”，但在实证研究中通常以“破产”为财务困境的标志（Ball、Foster，1982）。Beaver（1966）将“失败”定义为公司无法支付到期债务。从营运角度定义，下述事件只要有一个发生，公司即可宣告失败：破产、债券违约、透支银行账户或拒付优先股股息。Mears（1968）对上述构成经营失败的后三种情形有疑虑，因为债务违约可以被修正，银行账户透支问题可以得到妥善处理，优先股股息也可以重新计算，这三种情形并不一定与经营失败相关。

Deakin（1972）进一步将“失败”严格限定为正经历破产、由于资不抵债或其他原因被清算的公司。Ohlson（1980）对“失败”的界定拘泥于法律条文：失败企业是指根据美国《国家破产法》第十章、第十一章或其他预示进入破产程序的法律法规而申请破产的企业。Zmijewski（1984）将企业陷入财务困境定义为向法院提出破产申请的行为：如果一家企业在此期间递交了破产申请，则被认定为破产公司，否则为非破产公司。

随后Dietrich（1984）总结道：上述研究针对破产的定义是依据法律规定，而不是经济实质。但是破产在概念上并不是同质的，而是存在内部差异。有一些公司选择自愿破产（美国《国家破产法》第十一章），而有些公司可能是被债权人申请强制破产的（美国《国家破产法》第十章）。虽然这两类破产在法律处理上是相似的，但是经济条件可能完全不同。即使在这两种破产类型内部，人们对破产企业的同质性也有疑虑。更为重要的是，即使是破产企业也可能给股东带来正面收益。可见，以往文献仅根据经济状况将财务困境划分为破产与非破产可能过于简单。

此外，Ball、Foster（1982）提出，以破产为标准来定义财务困境，忽略了企业的实际场景：即使一个公司面临着长期现金流问题，它也拥有除破产之外的许多其他选择。如通过剥离相关业务或出售企业股份，重新制定企业目标或减少规模业务，或者变卖所有资产来获得收益，又或者寻求合并伙伴。

为规避将财务困境区分为失败与非失败公司的传统二元分类的概念缺陷，Lau（1987）将公司财务情况划分为五种状态：状态0，财务稳定；状态1，省略或减少派息；状态2，技术性违约和拖欠贷款；状态3，申请破产保护；状态4，破产清算。状态1～状态4属于陷入财务困境的境地，其严重程度逐步增加。

而国内，依据我国上市公司制度背景，学术界通常把“ST公司”定义为财务失败企业（陈静，1999；陈晓、陈治鸿，2000；张鸣、张艳，2011）。所谓ST公司（Special Treatment），指的是按证监会［1998］6号文《关于上市公司状况异常期间的股票特别处理方式的通知》对“状况异常”的上市公司实行股票交易的特别处理。而“异常状况”通常是指“连续两年亏损”或“每股净资产低于股票面值”。事实上破产企业的结局有两种：重组和清算。据统计，大约30%的破产上市公司会重组成功（Casey et al.，1986）。上市资格仍然是一种珍贵的“壳”资源，所以即便上市公司面临破产，也会有其他实体对其重组。因此ST公司作为发生财务困境而重组的先兆，在我国制度背景下是测量财务困境的合格标志。

二、经营失败公司的特征

经营失败的公司不仅现金流较低，而且现金（速动资产）储备较少。失败公司偿还债务的能力较弱，但是它们反而更倾向于举债融资（Beaver，1966）。

经营失败的公司在破产前3～4年往往会快速扩张且融资来源是债务和优先股，而不是普通股或留存收益，募集的资金也是投入厂房和设备而不是流动资产。此后，公司不能产生足够的营业收入和净利润来支撑这些沉重的债务，于是它们的总资产在破产前三年迅速减少（Deakin，1972）。

三、财务困境的预测因子

寻求能够警示公司是否会陷入财务困境的预测因子，一直是此类研究的重点。预测因子通常可以分为三类：会计数据、现金流数据、市场数据。

（一）会计数据

最初，Beaver（1966）选择现金流/负债总额、净利润/总资产、负债总额/总资产、营运资本与总资产比率、流动比率、非信用间隔6个财务比率来预测公司是否会经营失败。紧接着，Altaman（1968）收集了22个财务比率，并将其分为5个类别，包括流动性、盈利能力、杠杆率、偿付能力和营运效率比率。依据每个预测因子对整体判别函数的贡献，经过迭代选择，最终将预测因子确立为：营运资本/总资产、留存收益/总资产、息税前利润/总资产、营业收入/总资产。对于财务困境的预测变量，可以确定四个统计显著的基本因素：公司规模、资本结构、绩效、流动性（Ohlson，1980）。

Ohlson（1980）认为，会计数据的“预警”作用有限。他发现，13个被误分类为破产的公司中，11个有正的营业利润，剩余2个亏损并不明显，并且财务状况良好（资产负债率分别为23%和37%）。一些公司甚至在破产前一年支付股息。此外，审计师并没有关注持续经营问题，出具了11份无保留意见和2份带强调事项段无保留意见的审计报告。

（二）现金流数据

越来越多的证券分析师、财经作家、会计政策制定者主张：对于公司经营业绩的反映，相对于损益表和资产负债表，现金流量表提供的信息更准确。但是Casey、Bartcak（1984）认为经营性现金流（Operating Cash Flow，OCF）并不是一个很好的预测财务困境的指标。他们研究了290家公司（其中60家已经宣告破产），发现五年跨度的营运现金流量数据无法区分健康与即将破产的企业。对于破产的预测，经营性现金流的预测准确性远不及6个常规性权责发生制的会计指标的线性组合。Casey、Bartcak（1985）将经营现金流与权责发生制会计比率一同分析时，发现经营现金流数据并没有提高预测精度，原因在于经营性现金流比率的组内离散程度高。

经营性现金流对财务困境的预测能力较差，还可以归咎于大量非破产公司被错误归类为破产公司，而这些公司往往不会有太多经营现金流。所以诊断财务状况时，如果太依赖经营性现金流，很可能导致投资者和债权人将健康的公司误认为陷入财务困境的公司。这些公司在某些时期经营性现金流较少，但是大多数不会破产。比如成长型企业，在争取市场机会和赢得市场份额时，应收账款和存货较多，往往不能产生正的经营现金流。但是，只要债权人和股权投资者能够看到增长潜力，这些公司并不会出现营运现金短缺的问题。而一些成熟企业，即使经营性现金流出现短缺，也不意味着有危险。周期性公司就是一个典型的例子，这些企业经常在营运高峰期前消耗现金建立库存，如果按照经营现金流判定，即使是正常运营，预测结果也会显示企业即将陷入财务困境。相反，一些公司虽然报告了大量的、正的经营现金流，但这可能是处于生命周期后期的企业缩减业务投资并获得现金的结果（Casey、Bartcak，1984）。

然而，以上论述并不能说明现金流比率对财务困境预测没有效用，Casey、Bartcak（1984）提出，如果扩大现金流的界定范围（例如将经营性现金流扩展至现金流总额），则可能提高判别的准确性。例如Emery、Cogger（1982）断定总现金流的方差是预测企业生存能力的一个重要因子。在上述基础上，Gentry et al.（1985a）以Helfert（1982）开发的收付实现制现金流模型为依托，将现金流的8个组成部分纳入logit回归，得到了与Casey、Bartczak（1985）一致的结论：经营现金流比率不能有效区别破产与非破产公司，但是分配股利的现金流（DIV）可以。

更进一步，Gentry et al.（1985b）将净营运资本的现金流（NWCFF）用存货、应收账款、应付账款等5项加以替换，得到12项现金流比率预测因子，然后进行probit回归，发现投资、股利和应收账款现金流要素在5%的水平上显著，再将这12项现金流组成部分纳入9项权责发生制的财务比率模型进行probit回归，发现12项现金流比率能提供额外识别财务困境的信息。Aziz et al.（1988）的研究与Gentry et al.（1985b）类似，但不使用Helfert（1982）的现金流模型，而是依托Lawson（1971）开发的现金流恒等式，以财务困境对现金流恒等式的6个组成部分（经营现金流、净资本投资现金、税收现金、流动性变化、债权人现金流、股东现金流）进行多元判别分析和logit回归。他们发现，对于破产公司的判别效率，该模型（Cash Flow Based Model，简称CFB）与ZETA模型总体上差不多（破产前两年ZETA模型较好，而破产前3～5年CFB更优秀一些）。但是ZETA模型需要估计破产公司的先验概率以及破产成本，从这个角度来说，CFB模型更具操作性。

总结上述将现金流数据作为财务困境预测因子的文献可以发现，以现金流比率，特别是经营性现金流比率为自变量的预测模型并没有展现出其先进性。Casey、Bartcak（1985）推测，这只是 FASB（财务会计准则委员会）和其他人的一种主观判定——经营性现金流是一个预示企业陷入财务困境可能性的有效指标，并没有理论依据。这种主观判定来源于分析家的偏好——在评估企业财务绩效时，倾向使用现金流数据（Hawkins，1977）。

（三）市场数据

除了会计数据、现金流数据，市场数据也可以作为预测因子。Beaver（1968）较早尝试利用市场信息预测企业是否会陷入财务困境（破产），研究发现股票市场价格变化也可以预测企业破产，但是预测能力不如财务比率。然而，这并不说明市场忽视了财务比率所蕴含的信息。他发现，投资者（股票价格变化）对破产的预测比任何比率都要敏感，价格变化领先于财务比率变化，财务比率与股票回报预测正相关。

紧接着，Altman（1968）在财务困境的判定模型中引入了一个市场数据指标——股票的市场价值/负债总额的账面价值。与类似更常用的会计比率——净资产/债务总额（账面价值）相比，股票的市场价值/负债总额的账面价值更能有效地预测破产。

此外，Aharony et al.（1980）运用资本市场信息比较破产公司与非破产公司的风险和收益特征，发现破产前4年至破产前公司总风险显著上升，这主要是由公司私有特征引起的，而不是市场因素引起的。也就是说，风险的上升是主要归咎于公司的私有特征，对于破产公司来说，系统风险并不是一个有用的预测指标。因此，他们采用异常收益来衡量因私有特征进而衡量企业陷入财务困境的概率，并发现这种方法是可行的。

Ohlson（1980）对上述研究进行了总结：对于如何在多元模型中选择自变量，目前并没有经济理论提供支持，通常采用经验主义的方法来选择自变量（财务比率）。一种方法是使用在以往文献中发现的变量作为自变量（预测变量）；另一种方法是在开始时几乎纳入所有自变量，然后采用类似因子分析或逐步判别分析的方法来缩减自变量。实证结果往往是针对样本的具体示例，并不能代表它们是预测财务困境最合适的指标（Ball、Foster，1982）。

四、财务困境判别模型

构建财务困境预测模型的动机主要有两个：①考察财务要素与财务困境之间的关联；②在一定时间间隔内预测哪些公司会陷入财务困境（破产）。破产预测模型可以使用不同的估算方法，每种方法的基本假设不同，计算复杂度也不同。先前的研究表明，对于应该选取何种估算方法以及如何在各种方法之间进行权衡，学界并没有达成共识（Dietrich，1984）。

与经营失败征兆有关的正式研究出现在20世纪30年代。Smith、Winakor（1935）和后来的几项研究表明，与持续经营的实体对比，破产企业会表现出显著不同的财务比率测量值。此外，也有研究关注的是经历履行固定债务义务困难时公司的财务比率特征（Hickman，1958）。Beaver（1966）的贡献在于，首次通过经验数据证实了财务比率对于预测的有效性，特别是失败预测。

（一）单变量分析

Beaver（1966）检验了各财务比率是否符合正态分布，发现在公司失败前每一年，以现金流与总负债比率为代表的财务比率总是显著偏斜的，即使经过简单转变（如求对数和求平方根），变量仍不符合正态分布假设。因为大多数多元判别分析依赖于正态分布假设，所以Beaver（1966）只用单变量进行检验。

所谓的单变量分析（一元分析），就是只用一个财务比率来预测一家公司是否失败。Beaver（1966）将该方法命名为二元分类检验，其步骤为：首先，将每个比率按升序进行排列。其次，在队列中挑出一个最优分界点。如果一个公司的比率低于（或高于）最优分界点，该公司被归为失败；如果公司的比率高于（或低于）最优分界点，该公司被列为非失败。最后，在判别每家公司的未来状态之后，将预测状况与实际状况进行比较，计算出差错率。差错率越低，预测能力越强。确定最优分界点是一个反复试错的过程，该检验经常受到批评，因为它是事后选择分界点。在现实情况中，决策者并不具备这样的信息优势，必须对未来样本做出预测。在这种情况下，做出决策时样本最终是否会破产是未知的。

Beaver（1966）研究发现，预测失败能力最强的指标是现金流与总负债的比率。失败前1年预测正确率为87%，前2～5年分别是21%、23%、24%、22%。同时他也开发了一些多元判别分析模型，但是发现结果并不非常理想，他认为在某种意义上，最好的单变量模型的预测能力不弱于多变量模型。

单变量分析的缺点在于：第一，只关注一个指标，容易被经理人粉饰，以使公司表现出良好的财务状况（张鸣、张艳，2011）；第二，使用不同的财务比率对公司财务状况进行判定时，几个指标值的分类结果很可能会相互矛盾，导致无法做出判断。因此，Altaman（1968）对单变量模型进行适当扩展，融合几种预测方法，生成一个更为广泛接受的预测模型——多元判别分析。虽然其不如回归分析流行，但自从20世纪30年代以来，其已经被运用于多个学科。在早些年，多元判别分析主要运用于生物和行为科学，后来该方法成功应用于金融领域，如消费信贷评估及投资分类。

（二）多元判别分析

多元判别分析（Multiple Discriminant Analysis，MDA）是指依据个体特征，判别一个个体属于多个先验分组中的哪一个类别。它主要用于辨别和预测，其特征就是被解释变量以定性的形式出现。

1.基本原理。首先，建立清晰的组别，组别的数量既可以是两个，也可以是多个。然后，收集各组的个体数据。接下来，尝试构建个体特征的线性组合，使之能够最为有效地判别新个体的组别归属。如果一个特定对象（如一家公司），其个体特征（财务比率）可以在分析中进行量化，那么可以确定一组判别系数。当这些系数应用于实际财务比率时，就可以判断新的观测样本应属哪一个类别。

多元判别分析技术的优势在于，它可以考虑与企业相关的、共有的全部财务比率及其交互作用。而单变量判别分析每次只能使用一个财务比率。除此之外，多元判别分析还可以减少分析的空间维度。财务困境研究的多元判别分析多涉及两组，一组由破产公司组成，另一组由非破产公司组成。因此，检验可转化成最简单的形式：一维。在先验样本分为两组的情况下，线性多元判别分析（LMDA）生成一个线性判别函数（Linear Discriminant Function，LDF），其形式为：

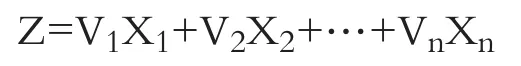
其中：V1，V2，…，Vn为判别系数；X1，X2，…，Xn为自变量；Z为判别值。

线性判别函数上的点代表来自两个不同组别的实体。通过这个线性判别函数，所有的p维空间观测值简化为一维空间观测值，并使两组在线性判别函数上的点最大限度地分离。这个判别函数将样本的一组变量值转化为单个判别值（Z值），可以用Z值来判断样本属于哪一类别。当拥有一系列Xj时，可以用多元判别分析计算出辨别系数Vj。

Altaman（1968）基于过去的研究，收集了22个财务比率，并将其分为五个标准类别：流动性、盈利能力、杠杆率、偿付能力和营运效率比率。考虑各预测变量对整体判别函数的贡献，经过迭代选择，确立的最终判别函数如下所示：

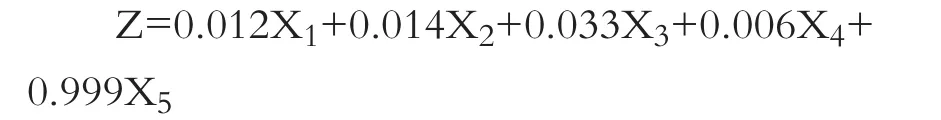
其中：X1为营运资本/总资产；X2为留存收益/总资产；X3为息税前利润/总资产；X4为股票市场价值/负债总额的账面价值；X5为营业收入/总资产。

Altman（1968）通过观察初始样本中被判别模型错误分类的公司，得出以下结论：①所有Z值大于2.99的公司都不会破产；②Z值小于1.81的公司都破产了；③Z值在1.81～2.99之间的区域被定义为“未知区域”或者“灰色地带”，因为这部分公司很容易被错误分类。如果一家新公司的Z值在“未知区域”，将不能确定它的归属类别，因此需要为这部分公司建立正确的判别指南。

运用多元判别模型来预测企业破产表现出很多优点，但是银行家、信贷经理、高管、投资者通常无法掌握复杂的计算步骤。因此，有必要将复杂的计算机程序预测模型扩展为更简便的方法来预测企业破产的可能性，可以选择分界点或者最适宜的Z值。Altman（1968）以错误分类数量最小化作为判断依据，发现辨别破产公司和非破产公司的最佳分界点为Z值等于2.675。

Altman（1968）使用判别分析的方法，根据破产前1年数据计算出的判断准确率（公司是否会破产）达到了95%。然而，随着间隔年份的加大，模型的预测能力急剧下降。在经营失败前第2～5年判断的准确率分别为72%、48%、29%、36%，相对于Beaver（1968）的二元检验（只用一个指标，即现金流/负责总额比率），判别分析的差错率更高。基于此，Deakin（1972）提出了一个预测企业经营失败的优化模型：将Beaver（1968）使用的财务比率加入到多元判别分析程序中。

2.贝叶斯判别。Joy、Tollefson（1975）根据先验概率对财务困境企业进行判定。归属于组i的先验概率为pi，组i的个体误判为组j的代价为Cij，假设其目标是尽量减少期望误判总成本。Z的临界值为：

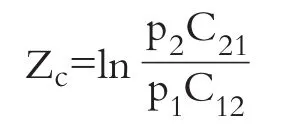
Altman et al.（1977）构建了适用于零售业和制造业的ZETA模型，其判定正确率（破产前1年为96%，而在破产前第5年为70%）优于其他模型。在确定临界值时，考虑了破产公司与非破产公司的先验概率（破产组q1=0.02，非破产组q2=0.98），还以商业银行贷款函数作为分析框架确定了第一类错误的误判成本（C1），为0.70，以无风险资产回报率确定第二类错误的误判成本，为0.02，根据公式，计算出临界点：

3.多元判别分析的步骤。假设有两个样本A和B，各自的样本规模为nA和nB。每个观察值有p维自变量。接下来，将样本A拆分为两个独立子样本A1和A2，各自样本规模为nA1和nA2。我们将A1称为分析样本（Analysis Sample），A2称为交叉验证样本（Cross Validation Sample），B为跨期验证样本（Inter-temporal Validation Sample）。

（1）通过分析样本（A1）拟合出一个线性判别函数（LDF），把判别函数的结果定为LDFA1。Altman（1968）就直接使用函数LDFA1对分析样本A1的个体进行判别。这种基于分析样本的判别结果并不能提供有意义的信息。

（2）通过交叉验证样本事后判别。事后判别指的是：用线性判别函数LDFA1对交叉验证样本（A2）进行分类。在金融研究中，一个最常见的错误是将这一步与预测相混淆。事后判别有助于解释过去，但是对于预测未来，它不能提供足够的证据。当然，如果假定总体是平稳的，不会随着时间而改变，这时事后判别相当于预测。

（3）如果事后判别结果良好，则需要根据子样本A1和A2重新合并后的样本A拟合出一个新的线性判别函数（LDFA）。显然，LDFA只是将系数更新，并没有更换新的自变量。

（4）跨时期验证。预测需要跨时期验证，而解释只需要交叉检验。事前预测是用线性判别函数LDFA对样本B进行辨别。一个成功的预测性线性判别函数模型对于样本B的观测值的分类成功率显著高于其他判别方案。

4.多元判别分析的缺点。多元判别分析也存在着一些问题：

（1）对于属性或者自变量的分布性质有某些特定统计要求。例如，不同组别的p维自变量的方差—协方差矩阵相等。此外，通常假定p维自变量（属性）符合多元正态分布。而有时自变量是虚拟变量，不符合该假定。

（2）多元判别分析中通常使用的样本“配对”程序存在一些问题。失败公司与非失败公司通常根据某种标准进行匹配，例如资产规模和行业。Zmi⁃jewski（1984）认为非破产的配对样本选择并不是一个随机抽样的过程，而是一个择机抽样：一个观测值能否被抽中依赖于特定属性（自变量）值。也就是说，研究人员需要首先观察某一属性特征，然后基于这种认知进行抽样。如果不使用适当的估计技术，这种抽样估计可能会产生参数以及破产概率的估计值偏差。平均而言，较低的破产公司采样频率会导致新观测值的估计破产概率较低。因此，降低破产公司的采样频率，会导致更低的估计常数、更低的破产公司分类正确率、更低的被分为破产公司的可能性，以及更高的非破产公司分类的正确率和更高的被认为是非破产公司的可能性（负相关）。当样本破产公司与非破产公司的比率接近总体时，偏差减少，而使用加权probit回归模型可以消除这种偏差。

（3）样本量太少导致结果不够稳健。Altman、McGough（1974）将Altman（1968）开发的Z指数模型运用于1970～1973年间28家破产公司。Altman（1968）报告的差错率大约为5%。同样的模型，只是样本所属年份不同，Altman、McGough（1974）报告的差错率为18%，可见Z指数模型可能缺乏稳健性。Moyer（1977）使用1965～1975年的数据重新检验Altman（1968）的模型［Altman（1968）的样本期间为1946～1965年］。Moyer（1977）报告的Altman（1968）Z指数模型的差错率达到了25%。因此Ohlson（1980）认为一个高质量的预测模型应在不同数据收集和估计程序下保持一定的稳健性。

为了克服这些局限性，多元逻辑回归（logit）和多元概率比回归（probit）被引入财务困境预测研究。

（三）logit预测分析

Ohlson（1980）选择了logit回归的计量经济学方法，将问题简化为已知一个公司具有某些性质（由财务比率指标呈现），计算它在一段时间内陷入财务困境的条件概率有多大。如果计算出的概率大于设定的分割点，则判定该公司在这段时间内会陷入财务困境（张鸣、张艳，2001）。该方法的优势主要在于：不用假定破产的先验概率以及自变量的分布。

X表示由自变量组成的向量。Xi为第i个公司的预测变量。β表示自变量的未知系数向量。P（Xi，β）为给定Xi、β时，第i个观测点破产的条件概率。就一个观测值i而言，可以将以Xi为条件的观测写成：

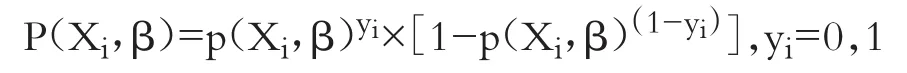
观测值i的对数似然可以写成：

通过运用极大似然法来估计模型的参数，对于一组样本其对数似然函数为：

其中，S1是破产公司组，S2是非破产公司组。对于特定的函数p，通过L（β）的最大值求得β系数的估计值β1，β2，…。对于原先的样本，根据求出的估计值β1，β2，…，计算出p的估计值，也就是陷入财务困境的概率p以及非破产的概率（1-p）。然后再寻找一个差错率最小化临界点。

Ohlson（1980）使用二分类probit回归和由1970～1976年105家破产公司和2058家非破产公司组成的非配对样本，分析了样本公司在破产概率区间上的分布以及两类判别错误和分割点的关系，总体差错率最小化的概率分界点为0.038，此时17.4%的非破产公司以及12.4%的破产公司被错误分类。

Lau（1987）使用多类别logit分析来构建财务困境预测模型。利用解释变量X预测每个公司的财务状况Zj，在这里有五种财务状况，j=0，1，2，3，4，5，Pj为一个给定的公司将最终进入状态j的概率。

（四）多维制图技术

Chernoff（1971）开发了制图技术，简单来说就是用一副面部表情描述K维空间中的一个点。面部表情的特征是由点的位置决定的，对于感兴趣的变量，首先经过简单的数学变化，再用其构造面部表情。例如，一个变量控制鼻子的长度，另一个变量控制鼻子的宽度。面部表情实际绘制由计算机程序控制。Moriarity（1979）运用多维制图技术描绘公司的财务状况。结果表明，相对于财务比率和财务报告，面部表情是一种传递财务数据信息更为有效的方式，也比Altman（1968）的多元判别模型更为有效。Altman（1983）认 为 Moriarity（1979）运 用 Altman（1968）的Z指数模型是不合适的，毕竟Z指数模型只适用于制造业而不适用于折扣连锁店。Altman、Haldeman和Narayanan（1977）的Zeta模型的预测能力更强。

（五）人工智能方法

20世纪90年代以后，涌现了大量人工智能理论模型，如人工神经网络（Odom、Sharda，1990）、遗传算法（Back et al.，1996）、粗糙集（Tay、Shen，2002）、案例推理（Jo et al.，1997）等。虽然这些方法具有较强的处理定性指标的能力和数据挖掘能力以及较高的预测效率，但是实证研究表明其并没有比多元判别分析、logit回归分析方法的判别能力更强，加上运算复杂、训练样本数量要求高、不能进行结构分析、结构不稳定、通用性差等缺点，限制了其在会计实务中的应用。

五、是否存在最优的判别方法

如果想对上述多元判别模型的预测能力按高低进行排序，则首先需要确定一个选择标准，即为什么模型A的预测能力比模型B好。以往评估模型的预测能力时，通常以两个非常具体和限制性假设为基础。第一，分类矩阵被认为能够充分反映模型的判别结果。第二，两种类型的分类错误具有可加性，错误率总和最小的那个模型是最佳模型。大多数研究都假定预测结果的两类误差所带来的成本是一样的，即认为一家公司破产与否的概率是一样的，而且将一家即将破产的公司预测为不会破产所带来的成本与将不会破产的公司预测为会破产所带来的成本是一样的。但是在进行判别分析的过程中，发生第一类错误的成本很可能远高于发生第二类错误的成本，并且需明确发生第一类错误与第二类错的概率。

由于时间间隔（从上一年年底到破产的时间）、预测因子（例如财务比率）、数据样本各不相同，预测结果也很容易受到估计方法的影响（例如是使用logit模型还是多元判别模型），所以很难在模型之间进行比较。事实上，各种统计方法的很多“合理的”优化措施致使判别效果都差不多（Ohlson，1980）。

六、小结

本文通过对国内外相关文献进行梳理和归纳总结，得到以下结论：财务困境、现金流风险、财务风险、破产、经营失败等概念在研究中通常可以互相替换，或者说其内涵是一致的，体现为以下几个方面：

1.概念标志物是一致的。在实证研究中，通常以“破产”或者“ST”上市公司作为标志物，来标记陷入财务困境、财务风险或现金流风险较大的企业。例如刘红霞（2005）将因“财务状况异常”而受到特别处理的A股上市公司作为现金流风险的界定标准。

2.内涵是一致的。财务危机、破产等发生的原因都是不能支付到期债务。财务危机（破产）是由众多因素交织在一起相互作用而导致的，事实上不论在何种情况下，财务危机都有共性的因素在发挥作用——现金流。企业生产经营能否持续的基本条件为是否获得了足够的现金流，现金流不足是企业发生财务危机的最重要的信号（刘红霞，2005）。现金流是一个企业的血液，一旦出现问题，就会引起“供血不足”，最终导致企业破产（何丹，2005）。

3.度量方法可以通用。早期的研究者根据其理论和实践经验使用了不同的财务指标构建度量方法，都可以用来预测财务困境、现金流风险。

Altman E..Financial Ratios，Discriminant Analysis and the Prediction of Corporate Bankruptcy［J］.Journal of Finance，1968（4）.

Altman E.，MCGough T..Evaluation of A Company as A Going Concern［J］.Journal of Accountancy，1974（6）.

Altman E..MultidimensionalGraphicsand Bankruptcy Prediction:A Comment［J］.Journal of Accounting Research，1983（1）.

Aziz A.，Emanuel D.，Lawson G..Bankruptcy Prediction-An Investigation of Cash Flow Based Models［J］.Journal of Management Studies，1988（5）.

Deakin E..A Discriminant Analysis of Predictors ofBusinessFailure［J］.JournalofAccounting Research，1972（1）.

Emery G.，Cogger K..The Measurement of Liquidity［J］.Journal of Accounting Research，1982（2）.

Joy M.，Tollefson J..On The Financial Applications of Discriminant Analysis［J］.Journal of Financial and Quantitative Analysis，1975（5）.

Lau A..A Five-state Financial Distress Prediction Model［J］.Journal of Accounting Research，1987（1）.

Moriarity S..Communicating Financial Information Through Multidimensional Graphics［J］.Journal of Accounting Research，1979（1）.

Ohlson J..Financial Ratios and the Probabilistic Prediction of Bankruptcy［J］.Journal of Accounting Research，1980（1）.

陈静.上市公司财务恶化预测的实证分析［J］.会计研究，1999（4）.

何丹.现代企业集团现金流风险预警体系的构建［J］.财会月刊，2005（17）.

刘红霞.企业现金流风险识别研究［J］.中央财经大学学报，2005（6）.

张鸣，张艳.财务困境预测的实证研究与评述［J］.财经研究，2001（12）.

王静，张进军.Z模型准确度影响因素实证研究——基于叶贝斯分类理论［J］.东岳论从，2013（6）.