一种基于GCV法改进的频域内位场正则化向下延拓的参数选取方法

刘 帆, 李正文, 种 洋

(1.61365部队，天津 300140；2.61206部队，北京 100042;3.信息工程大学 地理空间信息学院，郑州 450001;4.地理信息工程国家重点实验室，西安 710054 5.海军工程大学 导航工程系，武汉 430033)

0 引言

位场向下延拓是航空重力和磁力测量数据处理的重要技术，向下延拓能够突出局部场源，以此提高异常解释的可靠性；向下延拓也可用于构建高精度的空间地磁数据库以满足高精度地磁导航的需求。通常在空间域上的位场延拓算法面临着大型矩阵存储和运算困难的问题，因为借助FFT(快速傅里叶变换)的频域延拓算法具有计算快速和处理格网数据方便的优势[1]，所以频率域上的向下延拓方法一直是研究热点。2006年徐世浙[2]院士提出了积分迭代法，此法实现了大深度的位场向下延拓；刘东甲[3]将徐世浙的空间域迭代方法推广至波数域，得到了波数域迭代法。由于向下延拓问题是一个不适定问题，下延算子会放大观测数据中的高频噪声； Tikhonov[4]于上世纪60年代使用正则化方法给出了稳定的向下延拓频率响应；梁锦文[5]从四种频率响应的分析中得出了合适的频率响应公式。如今，反问题的正则化解法被广泛应用于位场的向下延拓，其延拓精度要优于绝大多数的延拓方法，但是正则化方法的实施难点在于正则化参数的确定，并且正则化参数对延拓精度有很大的影响。目前有关正则化参数确定方法的研究较少，马涛等[6]研究了基于L曲线法的位场下延正则化参数的选取问题；刘晓刚等[7]研究了重磁数据下延中的最优正则化参数确定方法；曾小牛[8]提出了基于径向谱的位场向下延拓正则参数选取方法。

正则化参数的选取方法大致分为先验选取和后验选取两大类，先验策略难以在实际应用中检验其成立的条件，因而确定正则化参数的后验策略研究具有很大的实用意义，目前在位场延拓问题的正则化求解中广泛使用的后验策略有L曲线法、GCV法(广义交叉验证法)、拟最优准则等。L曲线法是被普遍认为比较可靠的方法，但是基于频域的L曲线算法十分复杂；GCV法的计算比较方便快速，但由于将空间域中矩阵的求迹运算转换至频域内求解十分困难，所以GCV法在频域中难以实施，其他的方法几乎难以转换至频域内实现。笔者借鉴GCV函数值的计算形式，提出一种在频域内可实施的参数选取方法，并分别通过仿真数据和实测数据的向下延拓实验来进行验证，实验结果表明这种方法实用可行，且具有良好的延拓精度。

1 正则化参数选取方法

在向下延拓中u0(x,y)表示观测面上的位场数据，uh(ε,η)表示延拓面上的位场数据，h为延拓深度，由位场向上延拓的表达式[9]，可以得到：

(1)

式(1)可表示为卷积方程式：

u0(x,y)=Kuh(x,y)

(2)

其中:K为第一类Fredholm积分算子，使用Tikhonov正则化迭代法时，式(2)的解为[10]：

(3)

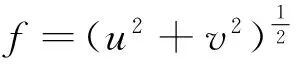
(4)

在式(3)、式(4)中α取值较大会使拟合误差过大，但α取值较小会使正则解过于接近原问题的不适定解而发生震荡，笔者使用L曲线法和一种新的方法来确定正则化参数，并比较使用这两种参数选取方法的延拓精度。

1.1 频率域的L曲线法

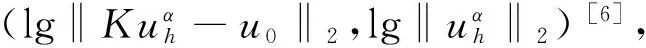
(5)

(6)

通常取L曲线的曲率最大点对应的α作为最优正则化参数，曲率计算公式如式(7)所示。

(7)

用一阶差分和二阶差分来代替函数ρ(α)、θ(α)的一阶导数与二阶导数。为了快速计算出c(α)序列，把ρ(α)、θ(α)转换到频域进行数值计算，根据Parseval等式，这两个函数的频域计算式如下：

(8)

(9)

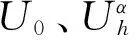
1.2 借鉴GCV法的构造泛函法

(10)

式中：

Hα=K(KTK+αI)-1KT

(11)

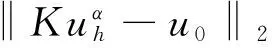
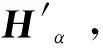
(12)

则有：

(13)

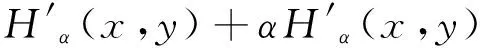
=K(x,y)*K(x,y)

(14)

对式(14)两端同时进行傅里叶变换，得到：

Φ(u,v)Φ(u,v)Gα(u,v)+αGα(u,v)=

Φ(u,v)Φ(u,v)

(15)

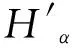
(16)

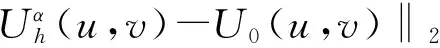
(17)

对比L曲线法，从式(16)、式(17)中可以看到，由于Φ(u,v)很容易求得,所以Gα是容易得到的,并且式(17)远比式(7)的计算流程少，计算更加简洁、易于实现。式(17)既满足了频域计算要求,又兼顾了方便快速计算的优点,笔者使用式(17)计算得到的V(α)最小值对应的α为最优正则化参数，为了验证此方法的正确性，分别使用仿真磁异常数据和实测磁异常数据进行了向下延拓实验(本文提出的参数选取方法为构造泛函法)。构造泛函法选取正则化参数求解位场向下延拓问题的流程图如图1所示。

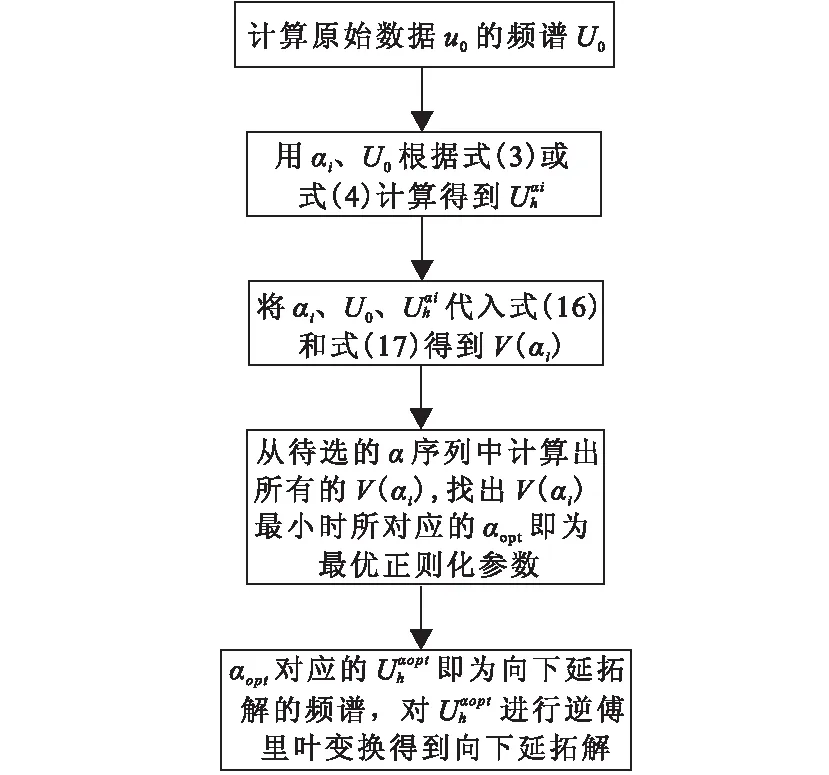
图1 构造泛函法用于正则化迭代法求解下延位场的流程Fig.1 The process for downward continuation using regularized iteration method with the constructing functional method

2 仿真数值实验

笔者使用球体磁异常正演模型生成仿真磁力测量数据[11]：

3x1z1sin 2IcosD+

3x1y1cos2Isin 2D-

3y1z1sin 2IsinD]

(18)

式中：取Z轴向上为正；μ0=4π×10-7H/m为真空导磁率；M为磁化强度；v为球体的体积；I为磁化倾角；D为磁化偏角；x1=x-x0、y1=y-y0、z1=z-z0；(x,y,z)是计算点坐标；(x0,y0,z0)为模型球体的球心坐标，实验所用球体磁异常正演模型参数见表1；分别生成高度为0m和100m的理论磁异常平面格网数据，每个平面上的格网间距为20m×20m,测点数88×88个，格网数据的统计特性见表2，实验中在高度为100m的格网数据中加入了标准差为3nT的高斯白噪声，然后将含噪声的数据向下延拓5倍点距，最后将延拓结果与高度为0m的磁异常理论值相比较，用平均相对误差(MRE)和均方根误差(RMSE)来评价不同参数选取方法的延拓精度，各观测面数据等值线见图2。为了减小边界效应，在进行延拓实验前，先对高度为100m含有噪声的格网数据使用了区域场[13]扩边法进行扩边处理，扩边点数为各方向20个，计算结束后再缩边20点得到向下延拓结果。实验中分别使用了Tikhonov正则化迭代法和Landweber正则化迭代法进行向下延拓，两种迭代法的迭代次数均设置为20次，Tikhonov正则化迭代法中参数α是从首项α1为10-8、末项αN为1的等比数列中选取的，N=200；Landweber正则化迭代法中参数α是从首项α1为0.7、末项αN为2的等比数列中选取的，N=200；两种迭代法都分别使用L曲线法和本文提出的方法选取最优参数以做对照。

表1 球体磁异常模型参数

表2 不同高度面上理论磁异常数据统计

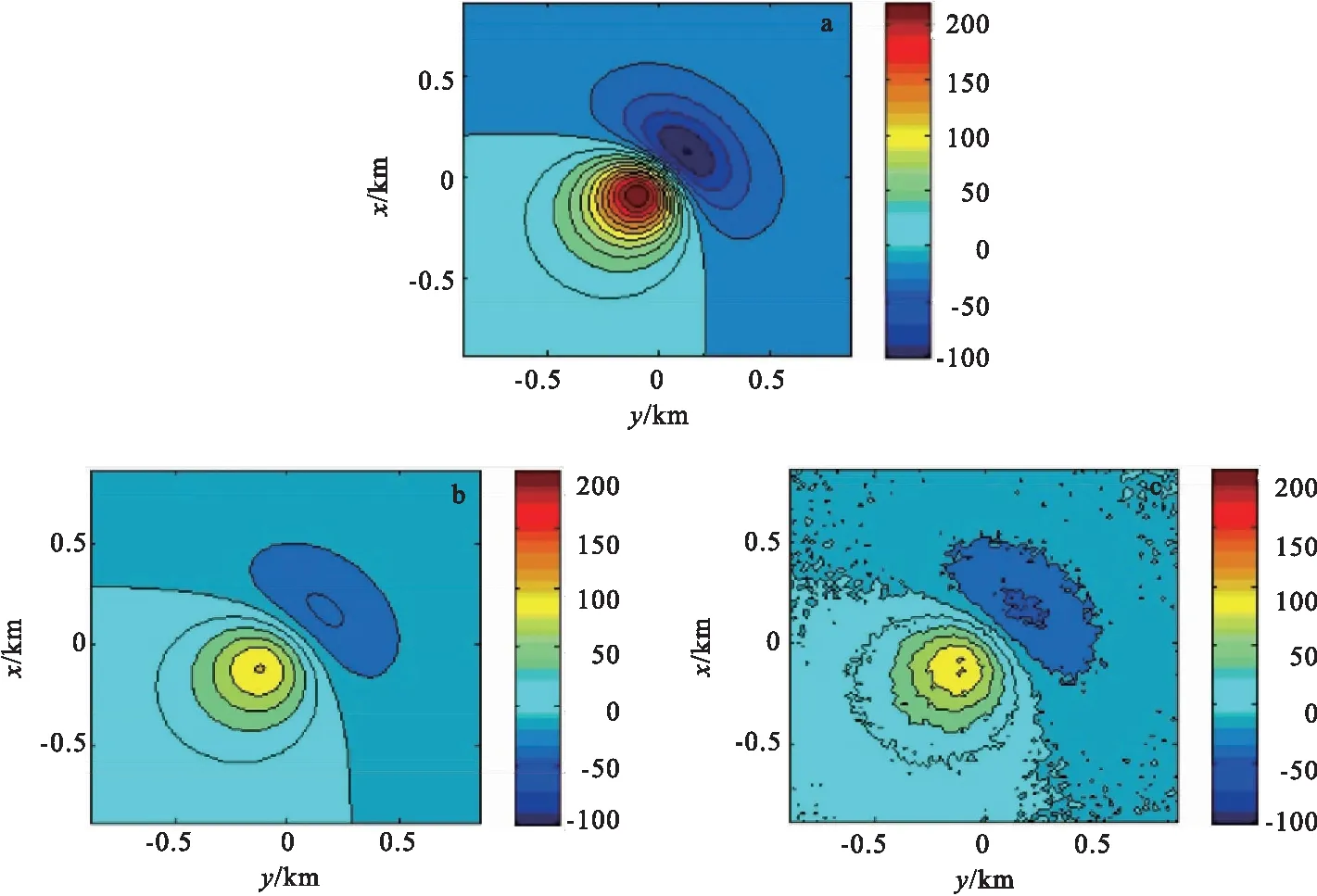
图2 各观测面上的磁异常理论值等值线图Fig.2 The contour map of magnetic anomaly on each observation plane(a)z=0 m理论磁异常；(b)z=100 m理论磁异常；(c)z=100 m含噪声理论磁异常

向下延拓精度统计见表3，Tikhonov正则化迭代法延拓结果等值线图的对比见图3，Landweber正则化迭代法延拓结果等值线图的对比见图4。Tikhonov正则化迭代法延拓结果过异常中心的剖面对比见图5(a)，Landweber正则化迭代法延拓结果过异常中心的剖面对比见图5(b)。

为了进一步比较和说明各个方法所选参数的优劣，统计了试验中两种迭代法迭代20次所对应的最优参数及其延拓精度(表4)。两种迭代法中根据式(17)计算出的V(α)值与参数α对应的关系曲线见图6。

表3 仿真数值向下延拓实验精度统计

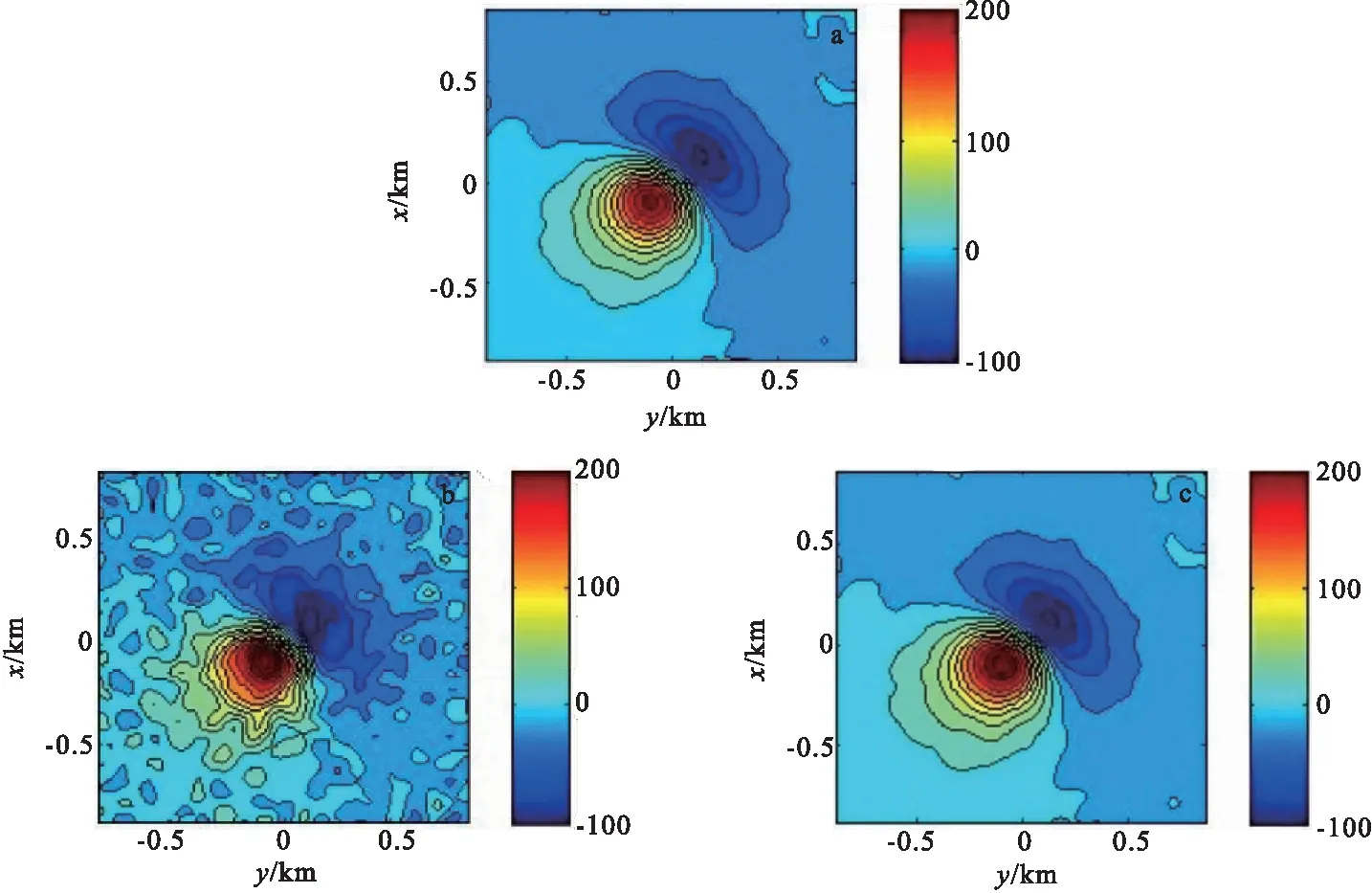
图3 频域Tikhonov正则化迭代法向下延拓结果等值线图Fig.3 The contour map of Tikhonov regularization iterative method’s downward continuation results in frequency domain(a)最优参数向下延拓结果；(b)L曲线法所选参数向下延拓结果;(c)构造泛函数所选参数向下延拓结果

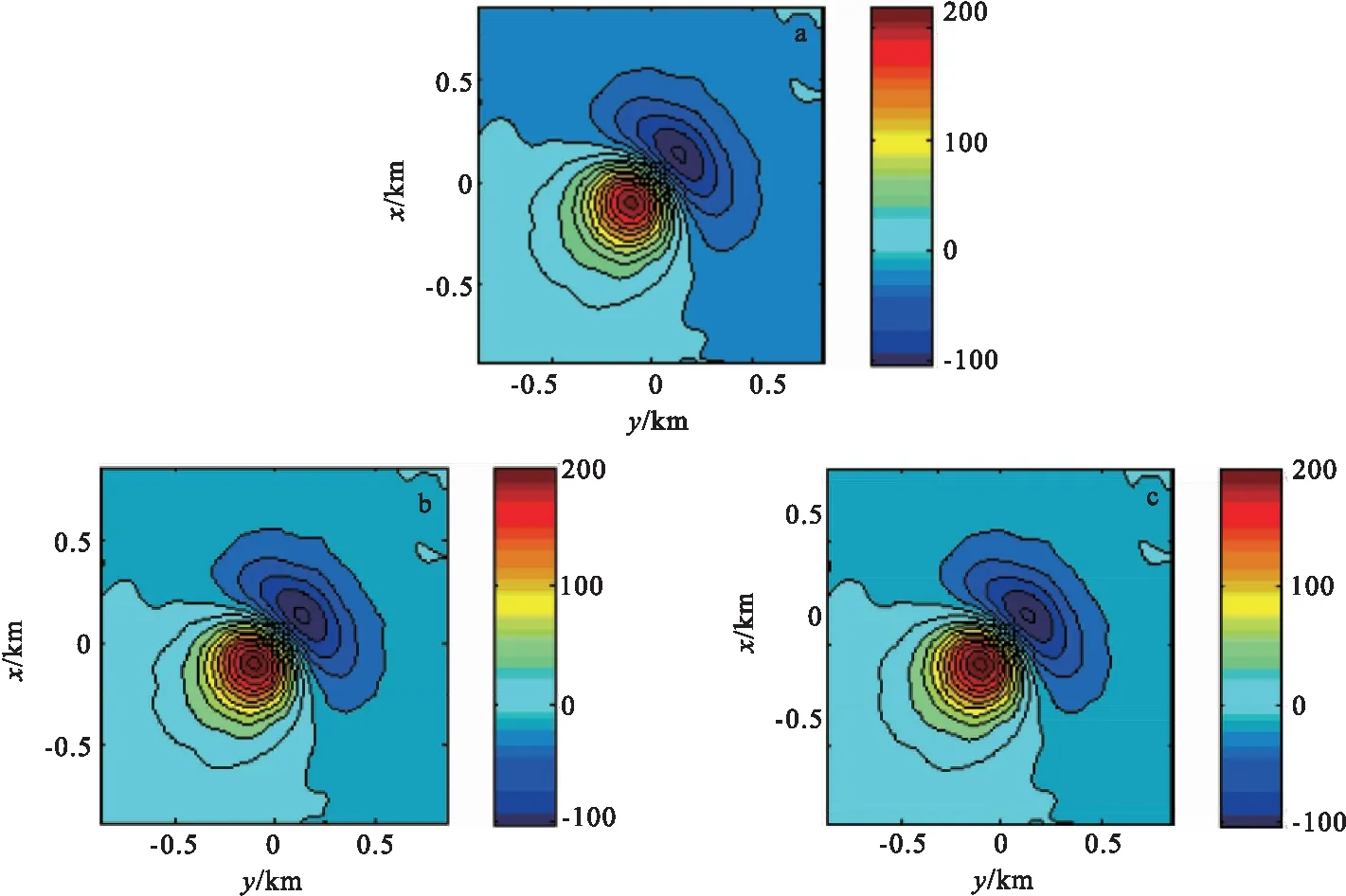
图4 频域Landweber正则化迭代法向下延拓结果等值线图Fig.4 The contour map of Landweber regularization iterative method’s downward continuation results in frequency domain(a)最优参数向下延拓结果；(b)L曲线法所选参数向下延拓结果;(c)构造泛函数所选参数向下延拓结果

迭代方法实际最优参数RMSE/nTMRE/%Tikhonov正则化迭代法0.39632.63126.76Landweber正则化迭代法1.94792.66886.85

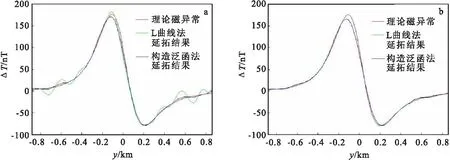
图5 频域内两种正则化迭代法向下延拓的剖面对比图Fig.5 Sectional comparison of two regularized iteration methods in the frequency domain(a)Tikhonov正则化迭代法延拓结果过异常中心的剖面对比;(b)Landweber正则化迭代法延拓结果过异常中心的剖面对比

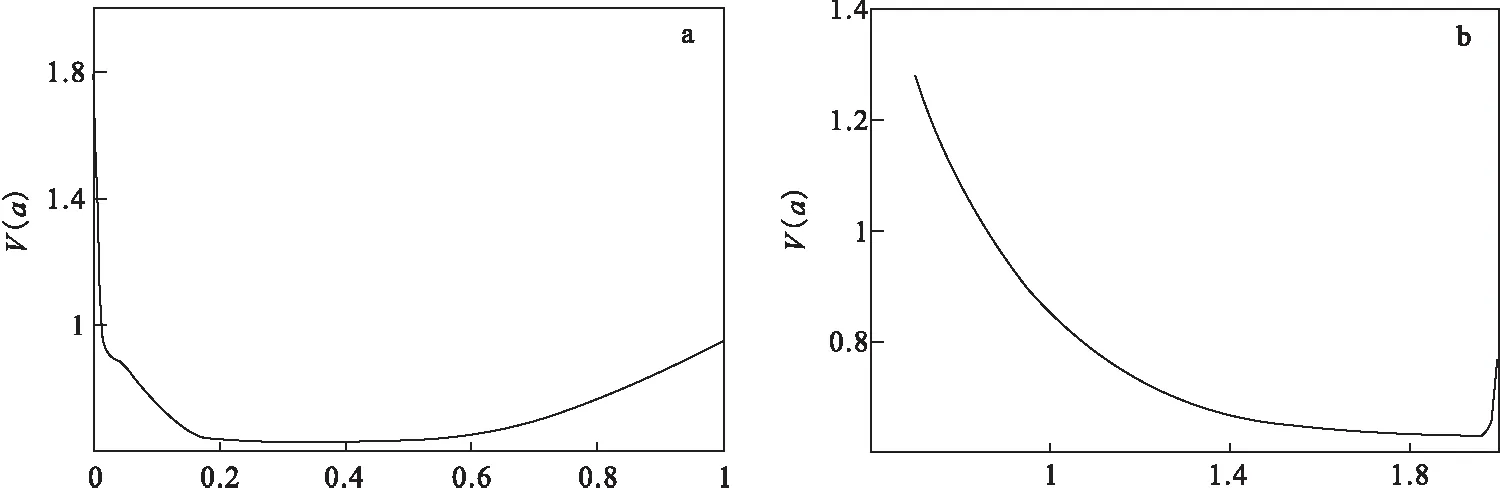
图6 频域内两种正则化迭代法向下延拓的α-V(α)曲线Fig.6 The α-V(α) curves of two regularization iterative methods’ downward continuation in frequency domain(a)频域Tikhonov正则化迭代法的v倍曲线；(b)频域Landweber正则化迭代法的v倍曲线

对比表3和表4，再结合图1～图4，可以发现在两种迭代法中，使用构造泛函法均比使用L曲线法得到的参数更优，均不同程度地提高了延拓精度；并且在这两种正则化迭代法中，使用构造泛函法选取的参数更接近实际最优参数，延拓精度也更接近最优延拓精度。对于Tikhonov正则化迭代法而言，使用构造泛函法选取参数的延拓精度比使用L曲线法的延拓精度有大幅度提高；对于Landweber正则化迭代法而言，使用构造泛函法选取参数的延拓精度比使用L曲线法的延拓精度有略微提高。从图6中可以看出，在Tikhonov正则化迭代法中，V(α)曲线在α∈(0.15,0.6)时较为平缓，曲线在极小值点附近变化很小；而在Landweber正则化迭代法中V(α)曲线是明显的先下降再上升的形态，在极小值点附近变化较为明显。

3 实测数据实验

笔者使用美国地质勘探局(USGS)海军科学研究实验所(NRL)于2008年在阿富汗实测的航空磁力资料进行数据处理检验。从官方网站上所下载到的数据，已经过数据预处理并被归算到离地面5 000m的高度。我们截取了东经64°～64.814°、北纬31°～31.814°之间的经过交叉测线改正后的磁异常观测数据进行延拓实验。试验中先将该区域内的数据处理成点距为1km的88×88点的格网(延拓前的原始磁异常格网)，然后将此格网向上延拓5倍点距后再向下延拓5倍点距至原高度，用向下延拓后的结果与原始实测格网异常数据进行比较并统计精度。试验中使用区域场法对原始格网数据进行扩边，扩边点数为20个，对计算得到的结果再缩边20个点得到向下延拓结果，向下延拓的实验方法与仿真数值试验方法相同。图7为用于延拓实验的原始磁异常格网，图8为分别使用L曲线法和构造泛函法选取参数的Tikhonov正则化迭代法的延拓结果。图9为分别使用L曲线法和构造泛函法选取参数的Landweber正则化迭代法的延拓结果。Tikhonov正则化迭代法延拓结果过异常中心的剖面对比见图10(a)，Landweber正则化迭代法延拓结果过异常中心的剖面对比见图10(b)。表5为延拓前的原始磁异常格网数据的统计特性，表6为实测航磁数据延拓实验的精度统计。

从表6中可以看出，在两种迭代法中使用构造泛函法选取参数的延拓精度都要优于L曲线法。在实测数据实验中，基于L曲线法选择参数的Tikhonov正则化迭代法的延拓精度明显好于仿真实验，因为上延是低通滤波过程，平滑掉了原始数据中的高频干扰，所以这一现象也说明了Tikhonov迭代法抗干扰能力比Landweber迭代法差。

对比表3和表6，可以看到无论是仿真实验还是实测数据实验，在Tikhonov正则化迭代法中，使用构造泛函法和L曲线法选出的参数相差较大，但是在Landweber正则化迭代法中，使用两种方法选出的参数相差不大，这说明在Tikhonov正则化迭代法中，构造函数法选取参数的优势更加明显，在实测数据实验中，所有方法的延拓精度都十分理想，平均相对误差均小于7%，相比图7，可以看到图8和图9中的延拓结果几乎没有明显的畸变和边界效应。

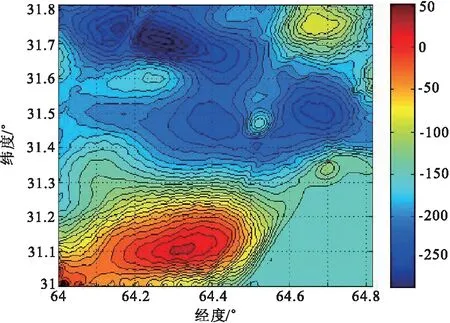
图7 原始磁异常数据格网Fig.7 The original magnetic anomaly data grid

观测面高度/m最小值/nT最大值/nT平均值/nT标准差/nT5000(原始异常)-282.690859.8296-151.906166.6123

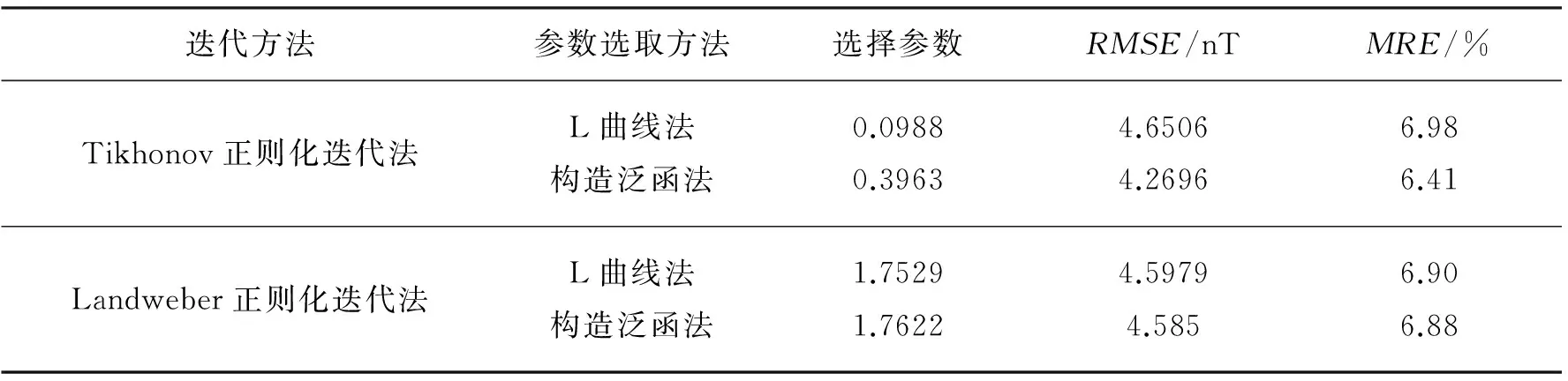
表6 实测航磁数据向下延拓实验精度统计

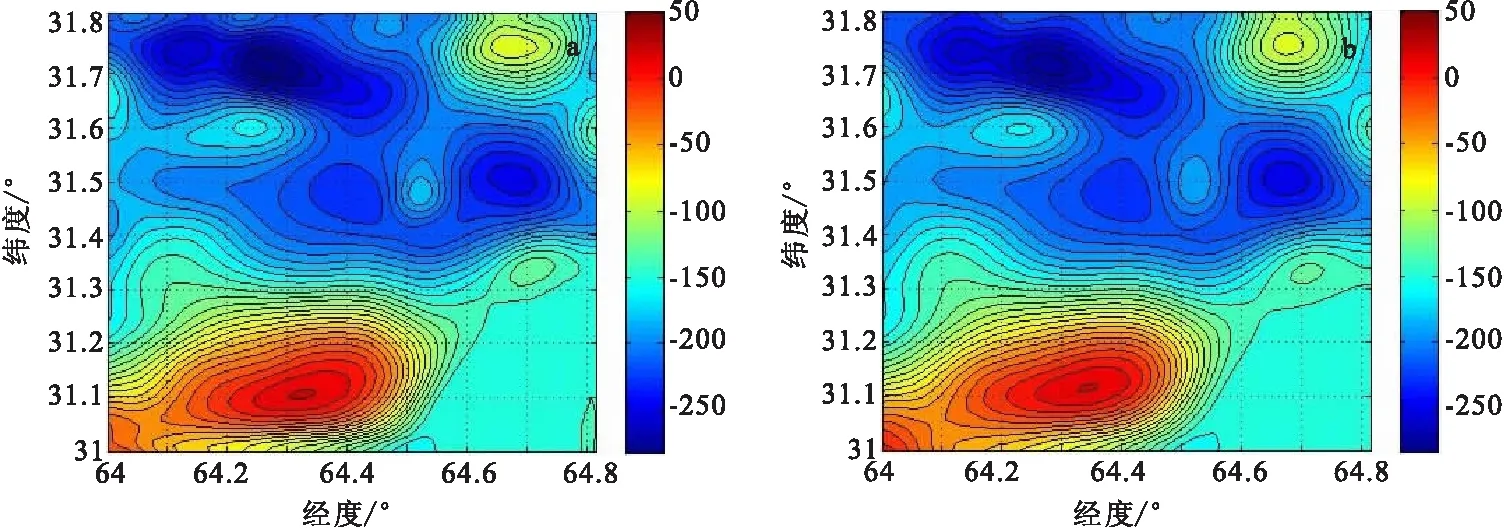
图8 频域Tikhonov正则化迭代法向下延拓结果等值线图Fig.8 The contour map of Tikhonov regularization iterative method’s downward continuation results in frequency domain(a)L曲线法所选参数向下延拓结果；(b)构造泛函数所选参数向下延拓结果

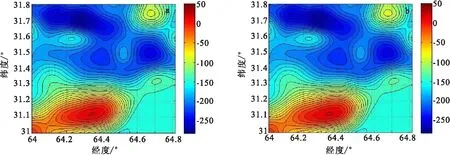
图9 频域Landweber正则化迭代法向下延拓结果等值线图Fig.9 The contour map of Landweber regularization iterative method’s downward continuation results in frequency domain(a)L曲线法所选参数向下延拓结果；(b)构造泛函数所选参数向下延拓结果

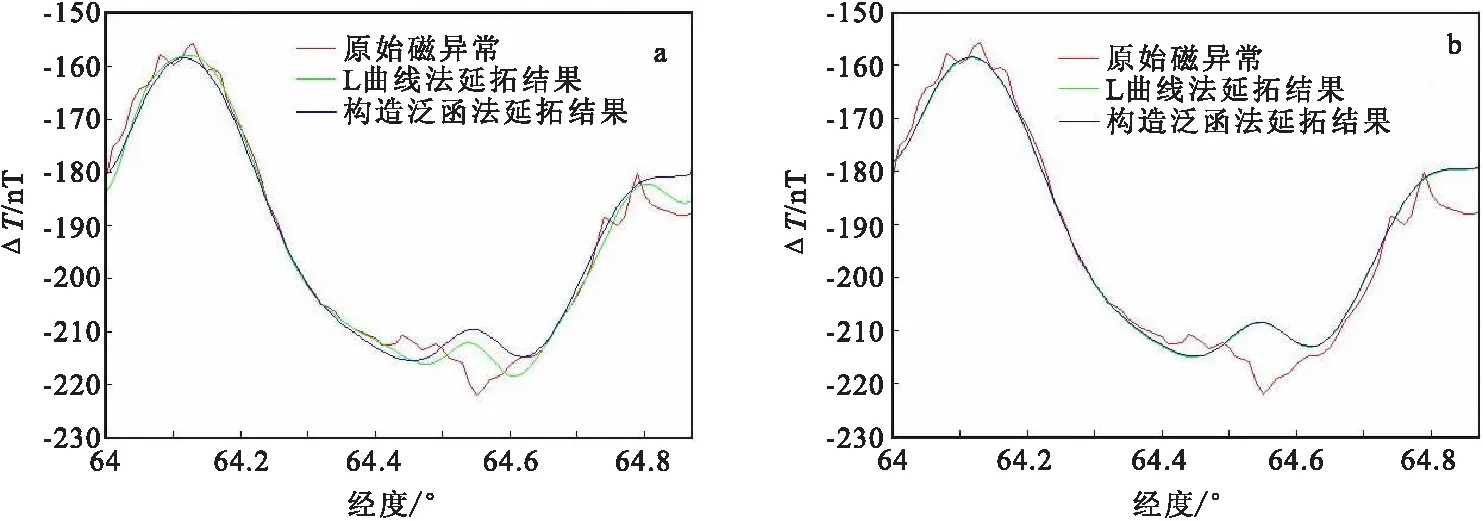
图10 频域内两种正则化迭代法向下延拓的剖面对比图Fig.10 Sectional comparison of two regularized iteration methods in the frequency domain(a)Tikhonov正则化迭代法延拓结果过异常中心的剖面对比;(b)Landweber正则化迭代法延拓结果过异常中心的剖面对比

4 结论

通过对仿真数值实验和实测数据实验的统计结果进行分析，得到以下结论：

1)在频域内使用正则化迭代法进行向下延拓时，使用构造泛函法选取的参数优于使用L曲线法选取的参数，使用Tikhonov正则化迭代法时，构造泛函法的优势更加明显。

2)相比L曲线法而言,构造泛函法的计算过程不涉及到求导运算，计算过程更加方便快速，并且具有更好的延拓精度。

3)构造泛函法选出的参数与实际最优参数十分接近，且在两种迭代法中选取参数的效果比较稳定，不同数据的延拓精度处于同一个水平。

[1] 周波阳,罗志才,许闯,等．航空重力数据向下延拓的FFT快速算法比较[J].大地测量与地球动力学,2013,33(1):64-73.ZHOUBY,LUOZC,XUC,etal．Comparisonamongfastfouriertransformalgorithmsfordownwardcontinuationofairbornegravitydata[J].Journalofgeodesyandgeodynamics,2013,33(1):64-73.(InChinese)

[2] 徐世浙. 位场延拓的积分-迭代法[J].地球物理学报,2006,49(4):1176-1182.XUSZ.Theintegral-iterationmethodforcontinuationofpotentialfields[J].ChineseJ.Geophys,2006,49(4):1176-1182.(InChinese)

[3] 刘东甲, 洪天求, 贾志海,等．位场向下延拓的波数域迭代法及其收敛性 [J].地球物理学报，2009,52(6):1599-1605.LIUDJ,HONGTQ,JIAZH,etal．WavenumberdomainiterationmethodfordownwardcontinuationofPotentialfieldsanditsconvergenee. [J].ChineseJ.Geophys,2009,52(6):1599-1605. (InChinese)

[4]TIKHONOVAN,ARSENINVY.Solutionofcertainintegralequationsofthefirstkind[J].JournalofAssociateComputerMachine,1962(9):84-97.

[5] 梁锦文.位场向下延拓的正则化方法[J].地球物理学报,1989,32(5):600-608.LIANGJW.Downwardcontinuationofregularizationmethodsforpotentialfields[J].ChineseJ.Geophys., 1989, 32(5):600-608 . (InChinese)

[6] 马涛,陈伟龙,吴美平,等．基于L曲线法的位场向下延拓正则化参数选择[J] .地球物理学进展,2013,28(5):2485-2494.MAT，CHENLW，WUMP，eta1．TheselectionofregularizationparameterindownwardcontinuationofpotentialfieldbasedonL-curvemethod[J].ProgressinGeophys,2013,28(5):2485-2494. (InChinese)

[7] 刘晓刚,李迎春,肖云,等．重力与磁力测量数据向下延拓中最优正则化参数确定方法[J] .测绘学报,2014,43(9):881-887.LIUXG,LIYC,XIAOY,etal．Optimalregularizationparameterdeterminationmethodindownwardcontinuationofgravimetricandgeomagneticdata[J].ActaGeodaeticaetCartographicaSinica,2014,43(9):881-887. (InChinese)

[8] 曾小牛,李夕海，陈鼎新，等．基于径向谱的位场向下延拓正则参数选取方法[J].石油地球物理勘探，2015,50(4):749-755.ZENGXN,LIXH，CHENDX,etal．Newregularizationparameterselectionforpotentialfielddownwardcontinuationbasedontheradialspectrum[J].OilGeophysicalProspecting，2015,50(4):749-755. (InChinese)

[9] 曾小牛,李夕海,韩绍卿,等．位场向下延拓三种迭代方法之比较[J].地球物理学进展,2011 ,26(3):908-915.ZENGXN,LIXH,HANSQ,etal.Acomparisonofthreeiterationmethodsfordownwardcontinuationofpotentialfields[J].ProgressinGeophys,2011 ,26(3):908-915. (InChinese)

[10]徐新禹, 李建成, 王正涛,等．Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J].测绘学报,2010,39(5):465-470.XUXY,LIJC,WANGZT,etal．ThesimulationresearchontheTikhonovregularizationappliedingravityfielddeterminationofGOCEsatellitemission[J].ActaGeodaeticaetCartographicaSinica,2010,39(5):465-470. (InChinese)

[11]骆遥,吴美平．位场向下延拓的最小曲率方法[J].地球物理学报，2016,59(1):240-251.LUOY,WUMP．Minimumcurvaturemethodfordownwardcontinuationofpotentialfielddata[J].ChineseJ.Geophys,2016,59(1):240-251. (InChinese)

[12]胡小平．水下地磁导航技术[M].北京:国防工业出版社,2013.HUXP．Technologiesonunderwatergeomagneticfieldnavigation[M].Beijing:NationalDefenceIndustryPress,2013. (InChinese)

[13]段本春, 徐世浙．磁(重力)异常局部场与区域场分离处理中的扩边方法研究[J].物探化探计算技术 ,1997,19(4):298-304.DUANBC,XUSZ．Astudyoftheschemeofextendingedgeintheprocessingofseparatinglocalfieldfromregionalfieldformagnetic/gravityanomaly[J].ComputingTechniquesForGeophysicalAndGeochemicalExploration,1997,19(4):298-304. (InChinese)