电导率连续变化二维海洋大地电磁场自适应有限元正演研究

潘林冬， 李予国,2*， 赵 慧

(1.中国海洋大学 海洋地球科学学院，青岛 266100;2.海底科学与探测技术教育部重点实验室，青岛 266100；3.国防科技大学,长沙 410073)

0 引言

大地电磁测深法(MT)是地球物理学中的一种重要探测方法。它根据电磁感应原理研究天然场源在大地中激励的电磁场分布，并由观测到的电磁场研究地球电性结构。大地电磁测深法在地壳和上地幔地质构造研究等领域应用广泛[1-3],在石油天然气勘探、地热和地下水资源调查等领域也发挥着重要作用[4-5]。1990年以来，大地电磁测深法已成功地应用到大洋中脊和大陆架地质构造研究中[6-8]。

岩矿石在形成过程中受湿度、含水率等多种因素的影响，这些因素将导致岩矿石的电导率连续变化[9]。电导率连续变化介质大地电磁场正演方法研究始于20世纪80年代。Kao 等[10-12]提出了层状介质电阻率随深度线性变化或指数变化时大地电磁场计算方法;徐世浙等[13]利用有限元法实现了一维分层电阻率连续变化介质大地电磁场正演。近年来，电导率分块连续变化介质二维和三维电磁场模拟研究也取得了一些进展。李予国等[14]用有限元法模拟了电导率分块连续变化二维大地电磁场响应；戴前伟等[15]讨论了电导率分块线性变化二维高频大地电磁场有限元正演模拟；阮百尧等[16]提出了电导率连续变化三维电阻率测深有限元模拟方法；李勇等[17]用有限元法模拟电导率分块连续变化三维可控源电磁场响应。

众所周知，结构网格难以精确模拟海底地形起伏和倾斜界面等复杂地质构造和地下复杂形状异常体。近年来，基于非结构网格剖分技术的自适应有限元方法在大地电磁场和海洋可控源电磁场数值模拟中取得了很好的应用效果[18-22]。赵慧等[23]研究了非结构三角单元网格自适应有限元海洋大地电磁场二维正演算法，它能够真实地模拟海底地形起伏、倾斜界面等复杂地质构造和地下复杂形状异常体，并能够克服海水与海底围岩巨大电阻率差异引起的数值模拟困难，提供可靠稳定的数值解。在自适应网格细化过程中，采用后验误差估计指导网格细化，只对具有较大局部误差的网格进行细化，从而减少了计算内存需求和节约了计算时间。我们将以上算法推广到二维电导率连续变化介质中，通过在有限元网格节点上进行电导率赋值，并且利用单元块属性区分开不同区域块体同一边界上的电导率赋值，使得它能够模拟电导率连续变化介质二维大地电磁场响应。

1 基本理论

1.1 大地电磁场的边值问题及有限单元法

考虑二维大地电磁模型，假设在x轴方向电导率保持不变，z轴垂直地表指向地下。平行走向电磁场分量满足如下偏微分方程[24]

▽·(τ▽u)+λu=0

(1)

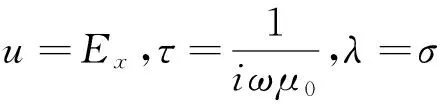
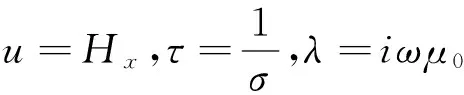
其中：ω为角频率；σ为电导率(S/m)；介质的磁导率μ0=4π×10-7H/m。

假定有限元模拟区域离二维不均匀体足够远，以致不均匀体产生的异常电磁场在其边界上衰减为零。在模拟区域左、右边界上可以采用Dirichlet边界条件，其电磁场表达式在文献[23]中已经给出。

二维大地电磁场边值问题与下列泛函极值问题等价[23-24]。

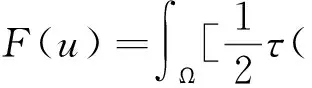
(2)

其中：Ω为模拟区域；Γ为模拟区域Ω的边界。

笔者采用三角网格有限单元法求解上述变分问题，将模拟区域Ω剖分成ne个三角形单元。由此，方程(2)的积分就转换为各个单元积分之和：

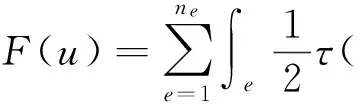
(3)

其中：Γe表示底边界CD上的线段；e表示三角单元。

在以往的数值模拟中，假定单元内的电性参数(τ和λ)为常数，即在单元内电性是均匀的，电性参数保持不变，但是连续变化的电性参数可能更符合实际情况。在我们的算法中，假定单元内电性参数(τ和λ)与电磁场u均是线性变化的，且可以近似为：

(4)

其中：ui、τi和λi分别是三角单元中第i(i=1,2,3)个节点上u、τ和λ的函数值；Ni是三角单元的形函数，其表达式如式(5)所示。

(5)

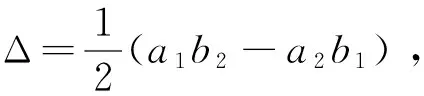
a1=z2-z3,b1=y3-y2,c1=y2z3-y3z2

a2=z3-z1,b2=y1-y3,c2=y3z1-y1z3

(6)

a3=z1-z2,b3=y2-y1,c3=y1z2-y2z1

方程(3)中第一个单元面积分可以写成式(7)。

(7)

其中：ue=(u1,u2,u3)T；K1e为单元矩阵

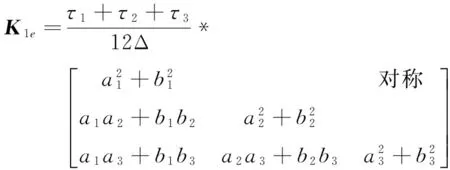
(8)

如果令式(8)中,τ1=τ2=τ3=τ,即得电性参数为常数情形的单元矩阵。

方程(3)中第二个单元面积分可以表示为式(9)。

(9)

(10)

如果令式(10)中,λ1=λ2=λ3=λ,即得电性参数为常数情形的单元矩阵K2e。

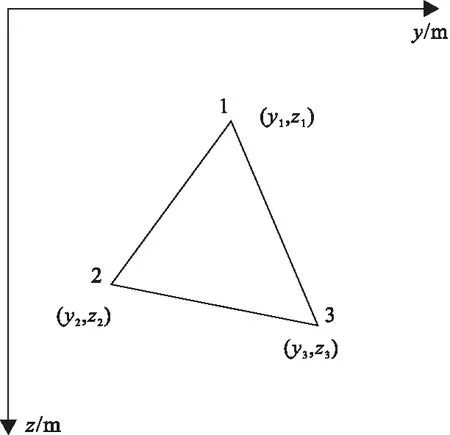
图1 线性插值三角单元Fig.1 Atriangular element

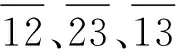
(11)

其中：K3e是一个3×3的对称矩阵，其非零元素为：

(12)

其中：

δ11=12τ1k1+3τ1k2+3τ2k1+2τ2k2

δ21=3τ1k1+2τ1k2+2τ2k1+3τ2k2

(13)

δ22=2τ1k1+3τ1k2+3τ2k1+12τ2k2

令式(13)中τ1=τ2=τ3=τ，k1=k2=k3=k，即得到CD边上电性参数为常数时单元矩阵K3e的元素。

计算得到每个单元的系数矩阵后，将其扩展和合并成总体系数矩阵为式(14) 。

(14)

于是得到泛函的离散形式为式(15)。

(15)

对方程(15)求变分得

KU=0

(16)

方程(16)的系数矩阵是对称的，但是奇异的。换句话说，需要代入边界条件，线性方程组才是唯一可解的。代入边界条件后，方程(16)变为式(17)。

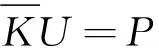
(17)

求解方程(17)即可得到电磁场平行走向分量。

由上述有限单元法得到的平行走向电场或磁场值的精度与网格紧密相关，合理可靠的离散网格设计是获得高精度数值模拟结果的关键。对于简单的地电模型，基于经验可以得到优化离散网格，而对于复杂模型，仅凭研究者的经验难以取得优化网格。新近发展起来的自适应有限元法能够自动细化网格,并提供可靠的数值解,该方法所涉及的主要技术是后验误差估计和自适应网格细化。

1.2 非结构网格和自适应有限元模拟技术

非结构网格具有更好地模拟海底地形起伏和地下复杂异常体的能力；自适应有限元模拟技术是指在得到的初始网格基础上，利用基于梯度恢复的后验误差估计对需要提高精度的网格进行加密，使得到的解满足精度要求。自适应有限元模拟涉及的主要技术问题，是后验误差估计和自适应网格细化。

本文算法采用基于梯度恢复的后验误差估计方法对有限元网格进行评判，指导离散网格的细化，提高解数值的精度[25]。在L2范数条件下，恢复梯度与有限元解的梯度之差为给定单元上的局部误差指示子:

ηe=‖(R-I)▽uh‖L2(e)

(18)

式中：R为一个梯度恢复算子；I为单位算子；▽uh为有限元解的梯度；恢复梯度为R▽uh。Bank等[26]提出了一种新的超收敛梯度恢复算子R=SmQh，其中Qh为L2投影算子，m为光滑算子平滑迭代次数(通常取2)。采用平滑算子Sm对Qh▽uh进行平滑，uh为分段线性的，因此▽uh是分段常数。随着单元减小，后验误差估计逐渐逼近真实的梯度误差[26]。后验误差估计表达式为式(19)。

ηe=‖(SmQh-I)▽uh‖L2(e)

(19)

基于局部误差指示子的网格细化，对于获得求解区域的精确解是合适的，可得到全局精度的解。但是在很多情况下，仅仅需要求得特定位置(如测点)的精确解[18]。如果想要减小测点处数值解的误差，需要考虑整个区域对局部误差的影响，可采用对偶加权误差估计方法[27]解决这个问题。

采用内积形式，将方程(1)转化成等价的变分问题，可得：

B(u,v)=0

(20)

其中：

(21)

式中：TE模式时u=Ex,k=1,q=iωu0σ；TM模式时，u=Hx,k=1/σ,q=iωu0。

定义泛函G为电磁场偏微分方程的精确解与有限元数值解的误差u-uh的函数，则有如下对偶方程为式(22)。

B*(w,v)=G(v)

(22)

这里B*(w,v)是对偶或伴随算子，假定B*(w,v)=B(v,w)，则有

G(u-uh) =B*(w,u-uh)

=B(u-uh,w)

=B(u-uh,w-wh)

(23)

其中：w和wh分别为对偶问题的解析解与有限元解。由式(23)可得:

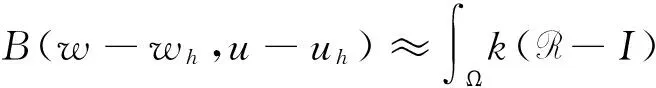
(R-I)▽uhdΩ

(24)

根据式(24)，定义基于对偶加权的误差指示子：

(25)

其中，

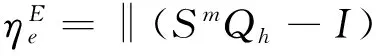
(26)

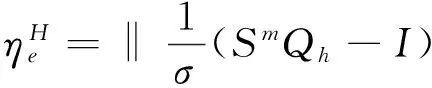
(27)

自适应有限元算法的基本思路如下：①将模拟区域进行初始剖分，产生一个粗糙的初始网格，并在该初始网格上进行有限元正演计算得到数值解；②计算每个单元的局部误差，选取一定比例具有较大局部误差的单元进行网格细化，产生一个新网格,并在新网格上进行有限元正演计算；③重复以上过程，直到有限元解满足假定的收敛精度或达到最大网格细化次数为止。我们设定的细化网格百分比为5%，收敛精度为1%。具体操作流程如图2所示。

2 算例

2.1 一维模型

为了验证本文算法的正确性及有效性,模拟一个三层地电模型(图3)的大地电磁测深响应。假定第一层和第三层的电导率分别为0.1S/m和0.01S/m，第一层的厚度为1 000m。第二层是厚度为500m的过渡层，其电导率随深度线性增加。

首先，按文献[24]中一维电导率连续变化有限元理论编写了程序；然后，对比程序计算结果与徐世浙《有限单元法》中的结果一致；最后，我们模拟电导率连续变化一维模型大地电磁场响应,并与一维电导率连续变化有限元算法结果进行比较。

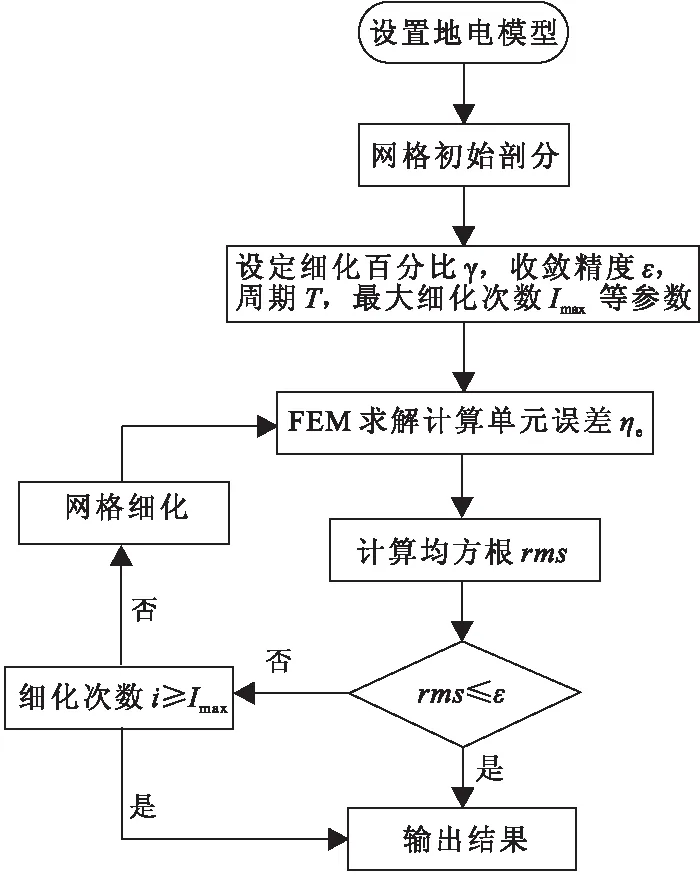
图2 自适应有限元正演算法流程图Fig.2 Adaptive finite element forwarding algorithm flow chart

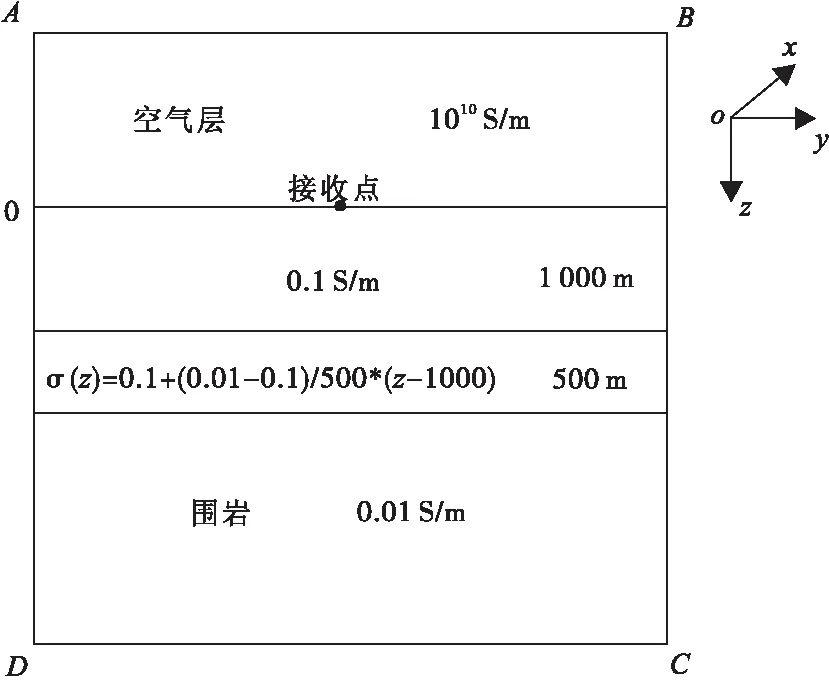
图3 一维电导率连续变化地电模型Fig.3 A 1D model with linear variation of conductivity

图4为笔者所述三角单元网格剖分自适应有限元算法得到的大地电磁测深视电阻率曲线和相位曲线，与用文献[13]一维有限元法及二维矩形网格剖分有限元方法所得计算结果的对比。由图4可见，三种方法的计算结果非常一致。

假定视电阻率相对误差和相位绝对误差为：

(28)

(29)

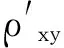
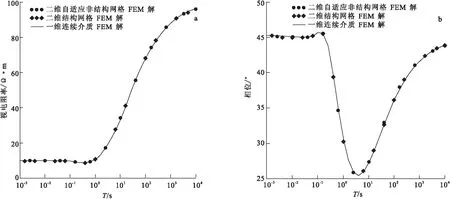
图4 一维层状模型大地电磁响应曲线Fig.4 Magretoele ctromagnetic response curve of one-dimensional layered model(a)视电阻率测深曲线图；(b)相位曲线

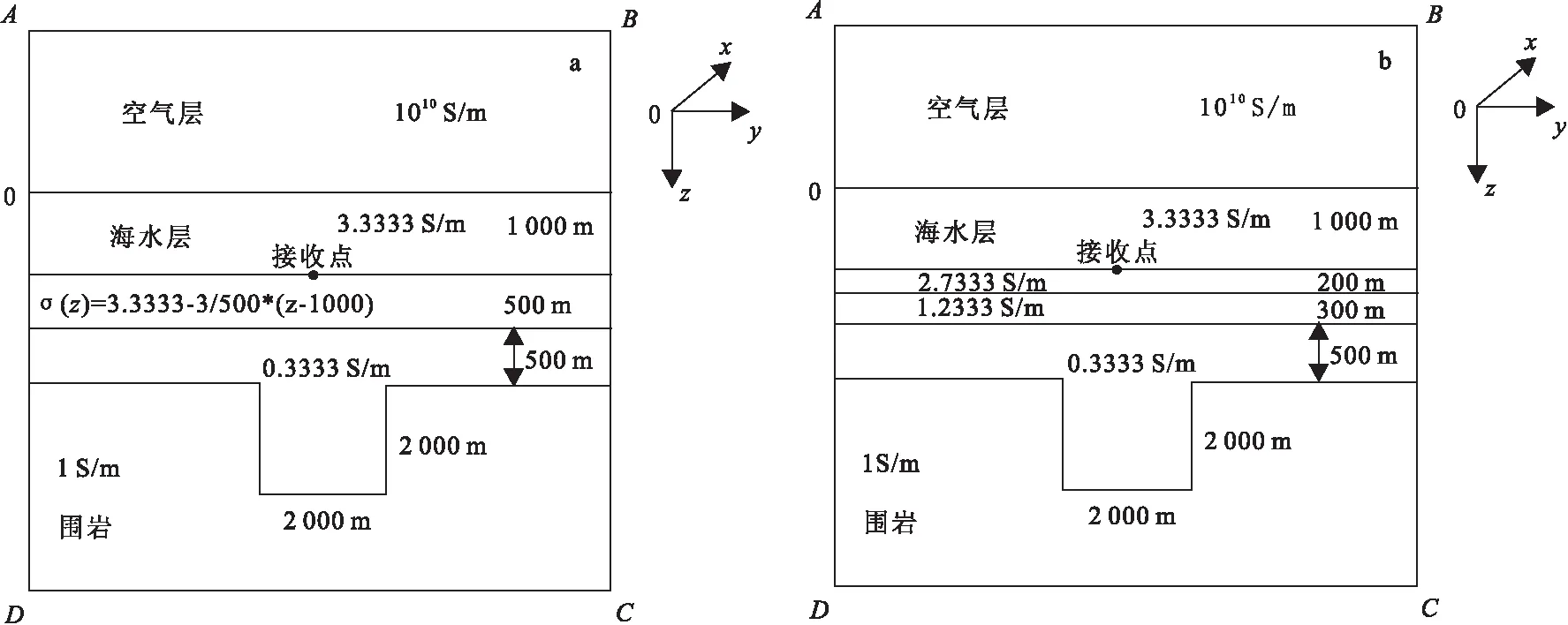
图5 等效二维地堑模型Fig.5 Equivalent two-dimensional graben model(a)二维含电导率连续变化层地堑模型图；(b)二维电导率分块均匀体地堑模型

2.2 二维地堑模型

图5(a)为一个四层地堑模型。第一层是电导率为3.333 3S/m，厚度为1 000m的海水层。第二层为500m厚的过渡层，其电导率随深度线性增加：

σ(z)=3.3333-3/500×(z-1000)

(30)

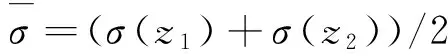
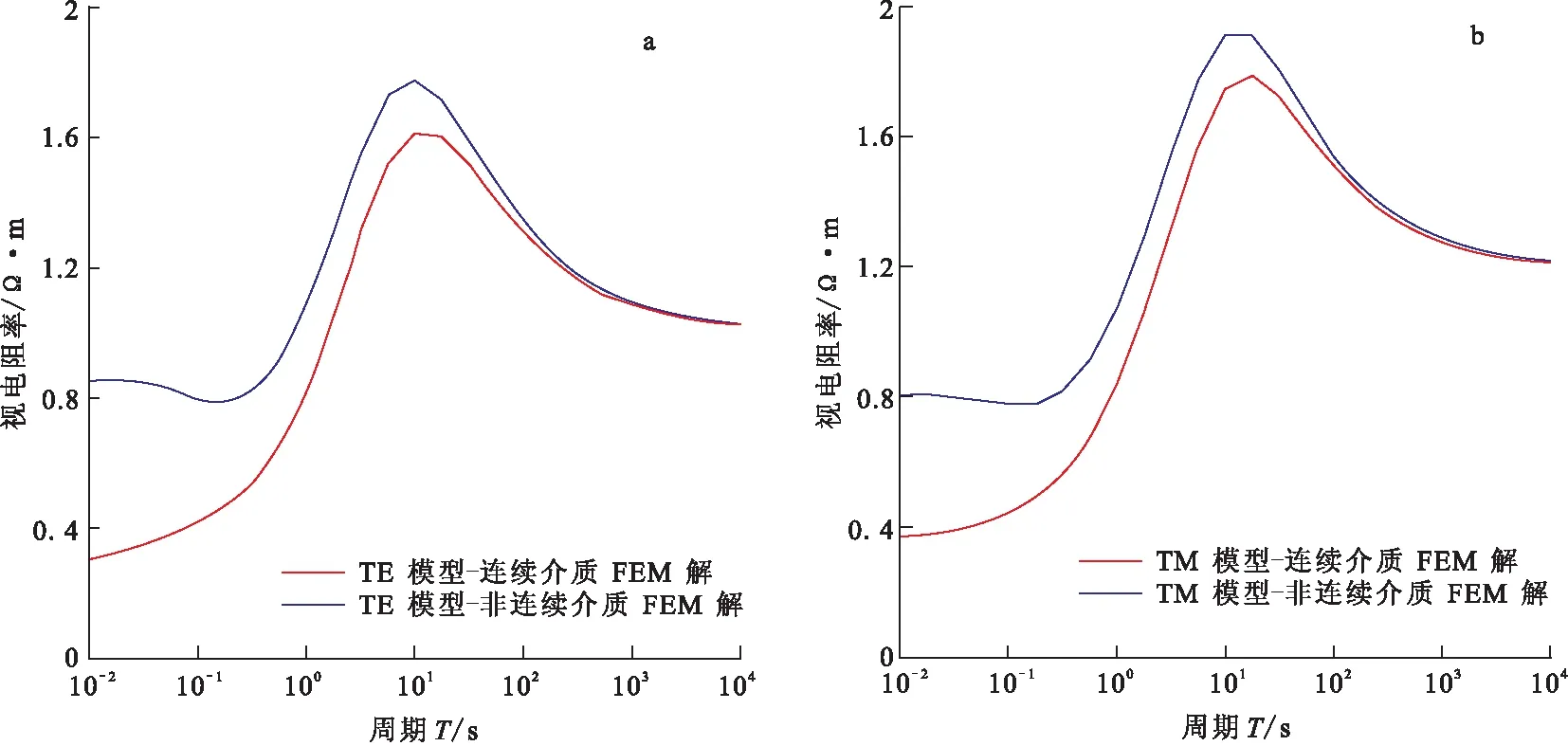
图6 视电阻率随周期变化曲线图Fig.6 MT apparent resistivities for TE mode and TM mode(a)TE模式；(b)TM模式

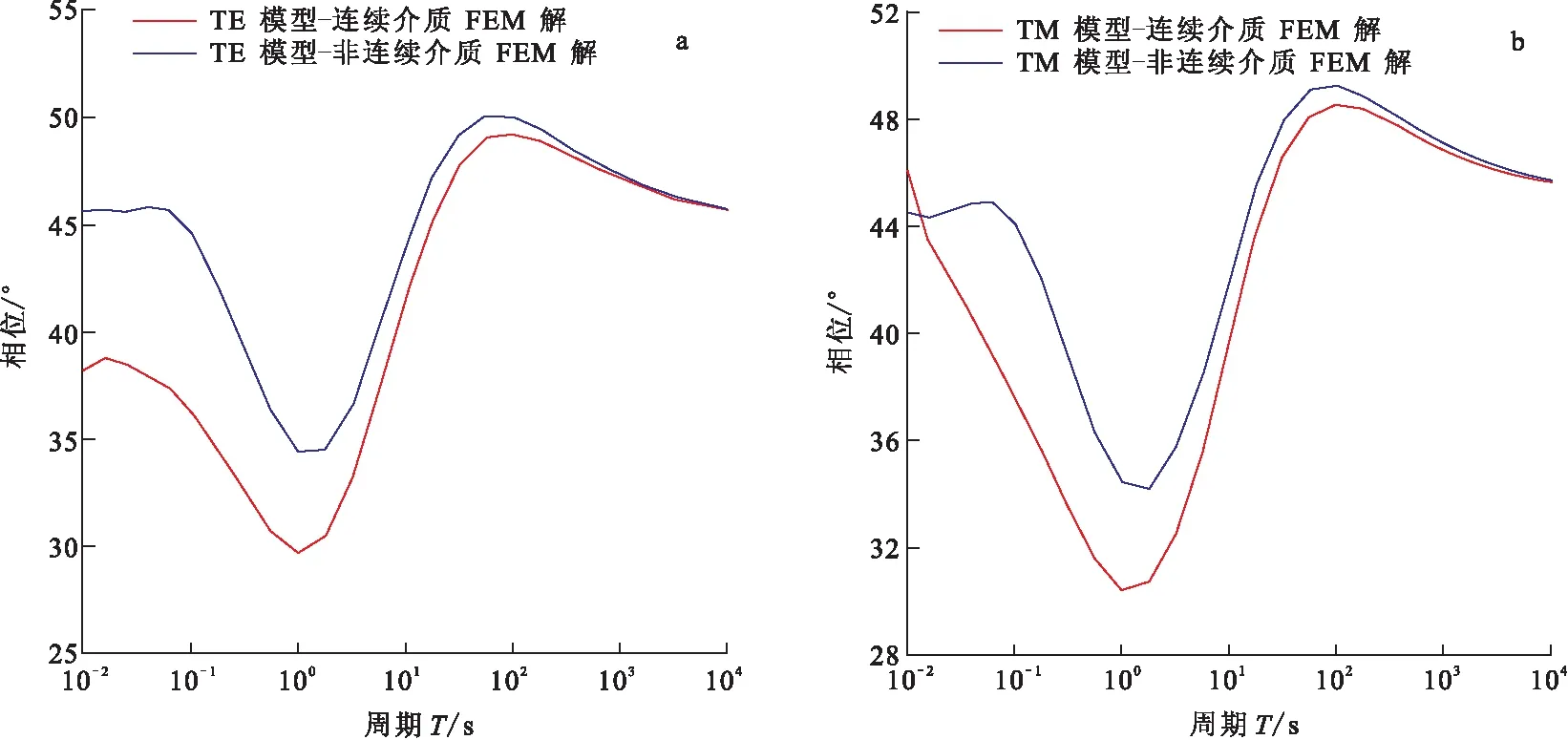
图7 相位随周期变化曲线图Fig.7 MT impedance phase for TE mode and TM mode(a)TE模式；(b)TM模式

2.3 复杂地电模型

设计一个如图8所示的复杂二维海洋地电模型，该模型关于y=0 m对称。海水层电导率3.333 3 S/m，厚度为1 000 m。在海底下方，有两个厚度各为1 000 m的电导率随深度线性变化水平地层。第一层的电导率随深度线性减少，由顶部处的3.333 3 S/m减小到底部处的0.333 3 S/m。第二层的电导率随深度线性增加，由顶部处的0.333 3 S/m增加到底部处的1 S/m。海底下方第三层是电导率为1 S/m的半空间，但其中含有一个形态较复杂的二维异常体。该异常体由上、下两部分组成，下面部分是电阻率为10 S/m的高导体，而上面部分电导率线性连续变化。

图9和图10分别为图8地电模型的初始网格和细化的最终网格，由图9和图10可以看出在接收站处网格得到了加密。

我们模拟了该模型的大地电磁测深响应。计算频率范围为10-4Hz～101Hz，计算频率点均匀分布，每个数量级取10个频点，总共计算了51个频率的大地电磁场响应。接收站在-15 000 m～15 000 m范围内按点距为500 m布设在海底，总共61个测点。

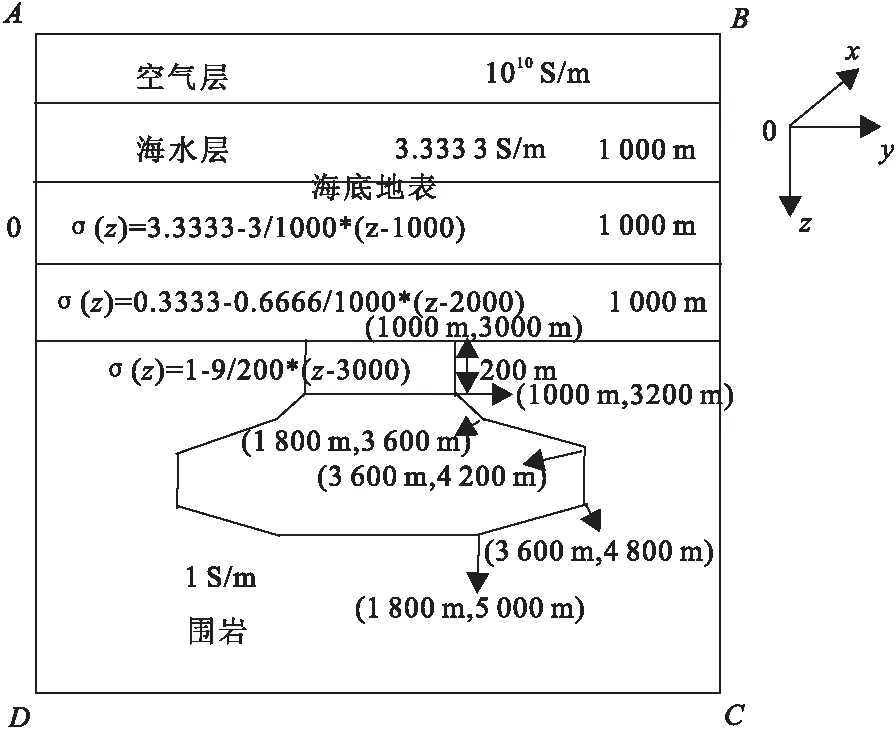
图8 二维复杂地质体电导率连续变化地电模型Fig.8 A two-dimensional model with linear variation of conductivity

图9 二维复杂地质体初始网格Fig.9 Initial mesh of two - dimensional complex geological

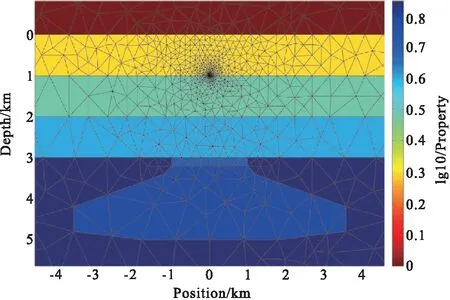
图10 二维复杂地质体细化最终网格Fig.10 Two dimensional complex geological body refinement final mesh

图11为TE模式大地电磁测深视电阻率和相位断面图。由图11可以很清楚地推断出深部高导体(低阻体)，也能看出海底下方两个电导率连续变化的水平层。图12为TM模式的视电阻率和相位断面图。对比图11(a)和图12(a)可知，TE模式深部视电阻率曲线是圈闭的，而TM模式视电阻率曲线在最下方并未圈闭，说明了TE模式对勾画异常体的范围效果更好些。

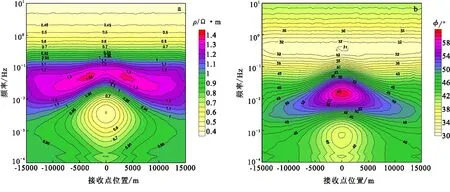
图11 TE模式视电阻率断面图和相位断面图Fig.11 TE mode apparent resistivity pseudosection and phase pseudosection(a) 视电阻率断面图；(b)相位断面图

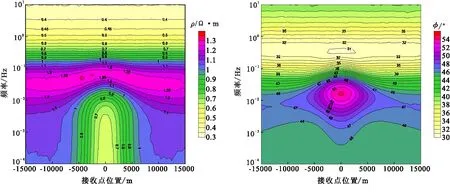
图12 TM模式视电阻率断面图和相位断面图Fig.12 TM mode apparent resistivity pesudosection and phase pseudosection(a) 视电阻率断面图；(b)相位断面图

3 结论

研究了电导率连续变化二维介质大地电磁场自适应有限元正演算法。与电导率分块均匀介质数值模拟方法不同，我们在单元节点上进行电导率赋值，在不同区域块体的相同边界的节点电导率利用区域块编号属性来区分，单元内各点处的电导率通过线性插值获到，从而使得我们能够模拟电导率线性连续变化介质电磁场响应。同时，由于采用了非结构三角单元网格剖分技术，我们的算法能够更好地模拟复杂地电模型。

致谢

感谢外审专家提出的宝贵意见，感谢刘颖博士的帮助和讨论。

[1] 马晓冰，孔祥儒. 青藏高原岩石圈热状态及其东西部差异[J].地球物理学进展，2001，16(3)：12-20. MA X B，KONG X R. The thermal status of Qinghai-Tibet plateau and the differen-ces between the western and the eastern plateau[J]. Progress in Geophysics，2001，16(3)：12-20.(In Chinese)

[2] 魏文博，邓明，谭捍东，等.我国海底大地电磁探测技术研究的进展[J].地震地质，2001，23(2)：131-137. WEI W B，DENG M，TAN H D，et al. Develo-pment of marine magnetotelluricprospe-cting technique in China[J]. Seismology a-nd Geology, 2001，23(2)：131-137. (In Chinese)

[3] 刘国栋. 我国大地电磁测深的发展[J]. 地球物理学报，1994，37(增刊1)：301-310. LIU G D. Delopment of magnetotelluric m-ethod in china[J]. Actageophysicasinic-a，1994，37(supp.1)：301-310. (In Chinese)

[4] 何展翔，贾进斗，苟量.非地震技术在油气勘探开发中的作用[J].石油勘探与开发，2001，28(4)：70-72. HE Z X, JIA J D, GOU L. The role of non-seismic techniques in exploration and development of oil and gas[J]. Petroleum E-xploration and Development，2001，28(4)：70-72. (In Chinese)

[5] 赵建良，陈天振，张晋，等. MT法在开封凹陷地热资源调查中的应用[J].物探与化探，2010，34(2)：163-166. ZHAO J L，CHEN T Z，ZHANG J,et al. The applic-ation of the MT method to the investin-gation of geothermal resources in Kaif-eng depression[J].Geophysical and Geoche-mical Exploration，2010，34(2)：163-166. (In Chinese)

[6] EVANS R L，LAW L K，LOUIS B S，et al.Theshallow porosity structure of the Eel- shelf, northern California: results of a towed electromagnetic survey[J]. Marine Geology，1999，154(1)：211-226.

[7] HOVERSTEN G H，CONSTABLE S，MORRISON H F. Marine magnetotellurics for base salt mapping: Gulf of Mexico field-test at the Gemini structure[J]. Geophysics，2000，65(5)：1476-1488.

[8] WORZEWSKI T，JEGEN K M，KOPP H，et al. Magnetotelluric image of the fluid cycle in the costa rican subduction zone[J]. Nature Geoscience，2011，4(2)：108-111.

[9] 李金铭.地电场与电法勘探[M].北京：地质出版社，2005. LI J M. Geoelectric field and electrical exploration[M]. BeiJing:Geological Publishing Ho-use，2005. (In Chinese)

[10]KAO D, RANKIN D.Magnetotelluricrespo-nse on inhomogeneous layered earth[J]. G-eophysics，1980，45: 1973-1802.

[11]KAO D. Magnetotelluric response on vertically inhomogeneous earth[J]. J. Geophys. Res，1981，86： 3027-3038.

[12]KAO D. Magnetotelluric response on vertically inhomogeneous earth having conductivity varying exponentially with depth[J]. Geophysics，1982，47：89-99.

[13]徐世浙，刘斌.电导率分层连续变化的水平层的大地电磁正演[J].地球物理学报，1995，38(2)：262-268. XU S Z，LIU B. A numerical method for calculating MT field on a layered model with continuous change of conductivity in each layer[J]. Actageophysicasinica，1995，38(2)：262-268. (In Chinese)

[14]李予国，徐世浙，刘斌,等.电导率分块连续变化的二维MT有限元模拟(II)[J]. 高校地质学报，1996，2(4)： 448-452. LI Y G，XU S Z，LIU B,et al. The finite element method for modeling 2-D MT fi-eld on a geoelectrical model with con-ductivity within each block[J]. Geologic-al Journal of China Universities，1996，2(4)：448-452.

[15]戴前伟，张富强，杨坤平，等.电导率分块线性变化的二维高频大地电磁法有限元正演模拟[J].物探化探计算技术，2012，34(5)：552-559. DAI Q W，ZHANG F Q，YANG K P. et al. Th-e finite element method for modeling 2-D high-frequency electromagnetic wit-h continuous of variation of conducti-vity within each block[J]. Computing tec-hniques for geophysical and geochemical exploration，2012，34(5)：552-559. (In Chinese)

[16]阮百尧，熊彬.电导率连续变化的三维电阻率测深有限元模拟[J].地球物理学报，2002，45(1)：131-138. RUAN B Y，XIONG B. A finite element mo-deling of three-dimensional resistive-ty sounding with continuous conductiv-ity[J]. Chinese journal of geophysics，2002，45(1)：131-138. (In Chinese)

[17]李勇，吴小平，林品荣. 基于二次场电导率分块连续变化的三维可控源电磁有限元数值模拟[J].地球物理学报，2015，58(3)：1072-1087. LI Y，WU X P，LIN P R. Three-dimensiona-l controlled source electromagnetic f-inite simulation using the secondary field for continuous variation of elec-trical conductivity within each block[J]. Chinese journal of geophysics，2015，58(3)：1072-1087. (In Chinese)

[18]KEY K，WEISS C. Adaptive finite-elemen-t using unstructured grids：The 2D magn-etotelluric example[J]. Geophysics，2006，71(6)：G291-G299.

[19]LI Y G，KEY K. 2D marine controlled so-urce electromagnetic modeling: Part 1-An adaptive finite element algorithm[J]. Geophysics，2007，72(2)：WA51-WA62.

[20]LI Y G，CONSTABLE S. 2D marine control-led source electromagnetic modeling: Part 2-The effect of bathymetry[J]. Geoph-ysics, 2007，72(2)：WA63-WA71.

[21]LI Y G，PEK J. Adaptive finite element modeling of two=dimensional magnetite-lluric fields in general anisotropic media[J]. Geophys J Int，2008，175(3)：942-954.

[22]LI Y G，DAI S K. Finite element modeli-ng of marine controlled-source electro-magnetic responses in two-dimensional dipping anisotropic conductivity struct-ures[J]. Geophys J Int，2011，185(2)： 622-636.

[23]赵慧，刘颖，李予国.自适应有限元海洋大地电磁场二维正演模拟[J].石油地球物理勘探，2014，49(3)： 578-585. ZHAO H，LIU Y，LI Y G. Adaptive finite element forward modeling for two-dimen-sional marine magnetotelluric field[J]. OGP，2014，49(3)：578-585. (In Chinese)

[24]徐世浙.地球物理中的有限单元法[M].北京：科学出版社，1994. XU S Z.Finite element method in geoph-ysics[M]. BeiJing:Science Publishing Company，1994. (In Chinese)

[25]刘颖. 海洋可控源电磁法二维有限元正演和反演 [D].青岛:中国海洋大学，2014. LIU Y. 2D finite element modeling and inversion for marine controlled-source electromagnetic fields[D]. Qindao: OUC，2014. (In Chinese)

[26]BANK R E ,XU J. Asymptotically exact a posteriori error estimators, Part I: Grids with superconvergence[J]. SIAM journal on numerical analysis, 2013,41(6):2294-2312.

[27]OVALL J S. Asymptotically exact functional error estimators based on superconvergent gradient recovery[J]. Numersische mathematic, 2006，102(3): 543-558.