基于GPU集群加速的电阻率三维数值模拟

杜 伟， 吴小平

(1.中国科学技术大学 地球和空间科学学院 地震与地球内部物理实验室，合肥 230026;2.蒙城地球物理国家野外科学观测研究站，蒙城 233500)

0 引言

直流电法作为一种重要的勘探手段，广泛应用于矿产资源勘察、水文地质等领域[1]。三维直流电法正演模拟作为反演的基础，计算速度直接影响反演解释的效率。正演主要的耗时步骤是大规模稀疏线性方程组的求解过程，在三维条件下共轭梯度迭代法较直接法更节省内存，计算时间更短，故被广泛采用[2-4]。

迭代法最后将稀疏线性方程组的求解归结为矩阵和向量的操作[14]。GPU作为一种向量处理机，适合大量并行线程同时进行，对于矩阵和向量的操作有天然的优势。CUDA(Compute Unified Device Architecture，统一计算架构)是NVIDIA公司推出的一种编程模型，将GPU的通用计算普遍化。CUDA在2006年刚推出时绑定了C语言，之后经过多年发展，现已支持MATLAB、Python、Fortran等语言。2009年PGI公司联合NVIDIA公司共同开发了支持FORTRAN的CUDA FORTRAN语言，保留了FORTRAN动态内存分配、模块、向量操作等特性；添加了可操作GPU的语句；提供了cuBLAS和cuSPARSE等函数库用于数值计算[5-6]。

国内、外学者在基于GPU的稀疏线性方程组求解方面做了很多研究，其工作主要围绕如何加快稀疏矩阵向量(Sparse matrix-vector multiplication, SpMV)，如何有效存储稀疏矩阵与如何使用GPU的不同层次的内存等问题展开[8,11]。目前，对于基于GPU集群的大规模线性方程组求解研究较少，主要有两个问题需要解决：①矩阵预处理，传统的IC/ILU/SSOR等预处理方法要求解三角线性方程组，其求解具有固有串行性[8]，不能有效地在多GPU上实现；②通信问题，NVIDIA推出的GPU-direct技术，实现了GPU在同一个节点内的GPU P2P直接通信，但跨节点的GPU数据传输需要将数据从GPU端拷贝到主机端，通过主机端的数据通信，然后拷贝到GPU端，数据通信延迟仍然是问题。

有学者使用了最简单的Jacobi预处理，在GPU集群上实现了共轭梯度法[9-10]，但Jacobi预处理在大多稀疏线性方程中效果不理想，有效的并行预处理方法有待研究。基于节点内GPU-GPU直接访问的技术，有学者实现了基于一个节点内的多GPU共轭梯度算法[9,11]。Cevahir 等[12]使用超图划分以及主机MPI通信实现了不同节点GPU的共轭梯度法；赵莲等[13]实现了基于多级k路图划分的GPU集群的近似逆预处理共轭梯度法，其他的基于GPU集群的共轭梯度法研究较少。以上的节点间GPU通信均通过CPU内存中转，效率较低。

MVAPICH2[19]是一个支持CUDA-Aware[7]的MPI通信实现，配合IB网络(InfiniBand network)可实现支持跨节点GPU到GPU直接通信。笔者使用可以并行的对称逐次超松弛迭代近似逆预处理技术，以及支持GPU-GPU通信的MVAPICH2 MPI，采用RCM算法将矩阵重新排序，减小矩阵带宽，提高数据局部性，成功解决了以上问题，并在GPU集群上获得了很好的扩展性。

1 三维电阻率数值模拟

当在地表使用双电极供电时，三维直流电阻率控制方程为：

▽·(σ▽φ)=-I[δ(r-r+)-δ(r-r-)]

(1)

其中：φ为电势；σ为电导率；r+和r-分别供电的正负电极位置；I为供电电流。采用非结构化网格离散研究区域，并在地表和其他边界面添加边界条件，采用有限元法求解上述控制方程的泛函极值最终得到大型稀疏线性方程组[3,23]：

Au=b

(2)

其中：u为三维离散网格各节点的电势；A为最终的组装矩阵；b为描述源分布的向量。A矩阵具有对称稀疏正定的特性(SPD)，且其维度较大，方程组一般采用稀疏存储并用迭代法求解。

2 SSORAI预处理

预处理可以降低原矩阵的条件数，加快迭代求解收敛。传统的SSOR预处理[14]具有构造简单、预处理效果较好的特点，但迭代过程中需要求解两个三角矩阵线性方程组，并行度不高。并行的预处理方法有矩阵稀疏近似逆(sparse approximate inverse，SAI)、多项式预处理(Polynomial Preconditioners)等[14]方法。对称逐次超松弛迭代近似逆[15](SSORAI)是一种近似逆方法，SSORAI预处理的思想即对SSOR预处理矩阵直接求逆，采用Neumann级数展开并截断的方法直接构造出近似逆矩阵。

对于对称矩阵A=E+D+F，考虑其SSOR预处理：

M=(D+ωE)D-1(D+ωF)=CCT

(3)

其中：D为对角线矩阵；E和F为上三角和下三角矩阵；0<ω<2为松弛因子，

C=(D+ωE)D-1/2

=D(I+ωD-1E)D-1/2

(4)

对式(4)求逆：

C-1=D1/2(I+ωD-1E)-1D-1

(5)

假设矩阵谱半径ρ(D-1E)<1，由Neumann级数展开：

C-1=D1/2(I+ωD-1E)-1D-1

=D1/2(I-ωD-1E+(ωD-1E)2-…)D-1

(6)

截取低阶项作为预处理矩阵的逆：

C-1≅D1/2(I-ωD-1E)D-1=K

(7)

所以SSOR预处理矩阵的近似逆为：

(8)

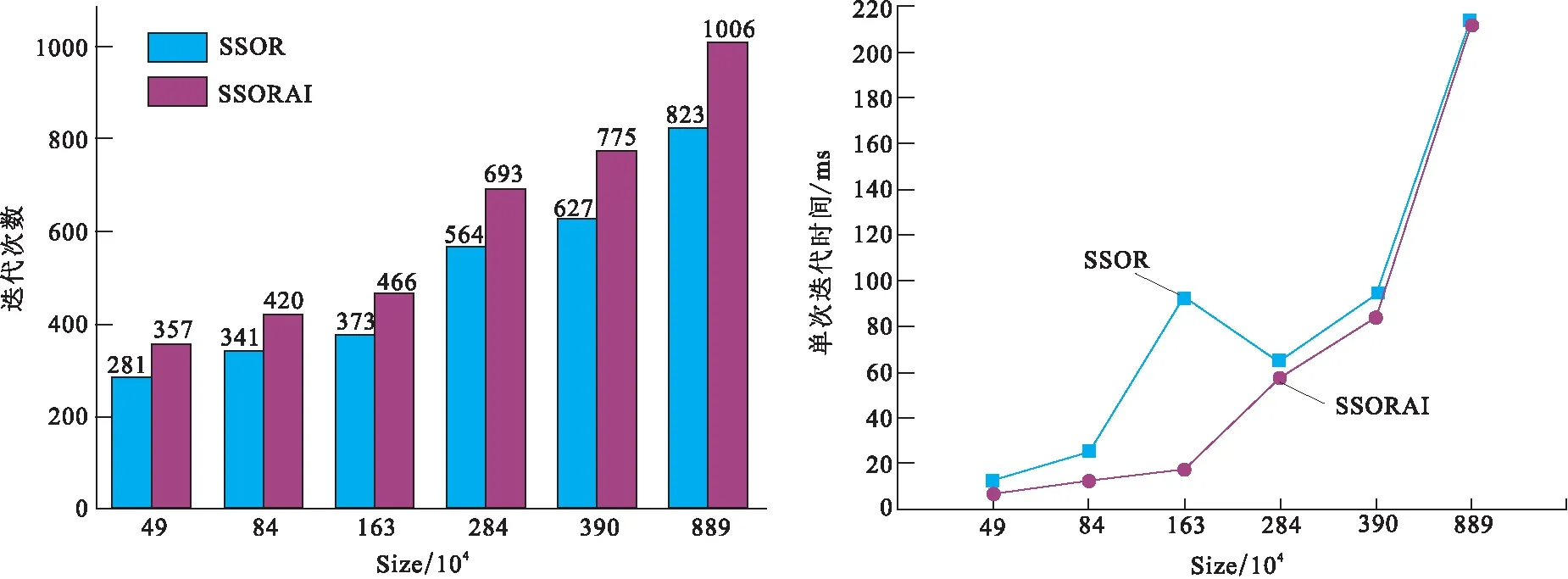
图1 SSOR预处理与SSORAI预处理效果对比Fig.1 Comparison of SSOR preconditioner and SSORAI preconditioner

图2 RCM排序效果对比Fig.2 Result of RCM sorting(a)未排序前；(b) RCM算法重排效果

3 基于GPU集群的实现

3.1 RCM排序

使用SSORAI预处理后矩阵可以采用矩阵行块划分的方式直接并行[17]，但是GPU间的通信仍是瓶颈。分析GPU间通信的原因，发现由于矩阵元素分布过于分散(图2(a))，迭代过程中SpMV需要使用到所有的向量，每次计算GPU都需要将所有的向量收集起来，导致通信量较大。为提高数据的局部性，减少GPU间数据通信，采用带宽缩减的方式减少矩阵带宽。常用的带宽缩减算法有CM算法[21](Cuthill-McKee algorithm)、RCM算法[16](reverse Cuthill-McKee algorithm)、GPS算法[22]等算法，考虑到RCM算法具有简单高效的特点，故采用之。

RCM算法将稀疏矩阵看作图的邻接矩阵，采用广度优先遍历的方式重新获取图的排列[16]，具体算法为：

1)确定一个起始节点r并令x1=r。

2)(主循环)从i=1、…、n，寻找所有与xi节点相邻并且未被编号的节点，并依次按照节点度增序编号。

3)(反序)将序列反序得到新的排序y1、y2、…、yn，其中yi=xn-i+1。

RCM算法时间复杂度与邻接矩阵的非零元个数成正比，计算时间较短,重排后的矩阵带宽极大地减少(表1)。

表1 RCM排序时间和带宽缩减对比Tab.1 Time of RCM sorting and bandwidth after the sorting

假设P为一个置换矩阵，则cond(PA)=cond(A),即置换矩阵作用于矩阵，变换后的矩阵条件数不变。RCM实质就是对矩阵进行置换操作，所以经过RCM排序后的矩阵条件数不变，即RCM排序不改变矩阵条件数，但可以极大地缩减矩阵带宽。

3.2 GPU集群计算和通信

经过RCM算法排序后的矩阵具有带宽有限的特征(图2(b))，在GPU集群上采用矩阵行块划分的方式，同时对相应的向量也进行连续划分，让各自的矩阵和向量在GPU内部使用，具体划分方式如图3所示。在共轭梯度算法中，向量的加减、内积等操作可以完全并行。但进行矩阵向量乘积时，每个GPU不仅需要自身的向量，还需要秩相邻的两个GPU的半带宽(half-band)的向量，例如秩为Rank 2的GPU进行SpMV时需要的向量为如图3中A+B+C的组合，需要通过MPI通信获取。MVAPICH2配合IB网络支持GPU到GPU的直接通信，但是通信时GPU设备空闲，造成资源浪费，通信延迟仍然是一个瓶颈。利用GPU通信和计算重叠，可以进一步提高程序效率。

为了利用通信计算重叠，将每个GPU负责的矩阵块划分为3部分(图3)矩阵块A、B、C，同时将向量也划分为三块，并在秩向量前后各扩展half-band的空间，以接收存储前后秩传递的数据。其中，各部分进行SPMV运算时，第一部分矩阵块A需要前一个秩的半个带宽向量，第二部分矩阵块B只需要自身的向量，第三部分C需要后一个秩的半个带宽的向量。为了编程的方便，在第一个秩前面和最后一个秩后面添加MPI的虚拟进程MPI_PROC_NULL[18](图3)。这样划分以后，计算和通信顺序为：计算矩阵块B的SpMV，同时通信向量第一块数据；等待通信结束，计算矩阵块C的SpMV，同时通信向量第三块数据；等待通信结束，计算矩阵块A的SpMV，从而完成整块矩阵的SpMV计算。

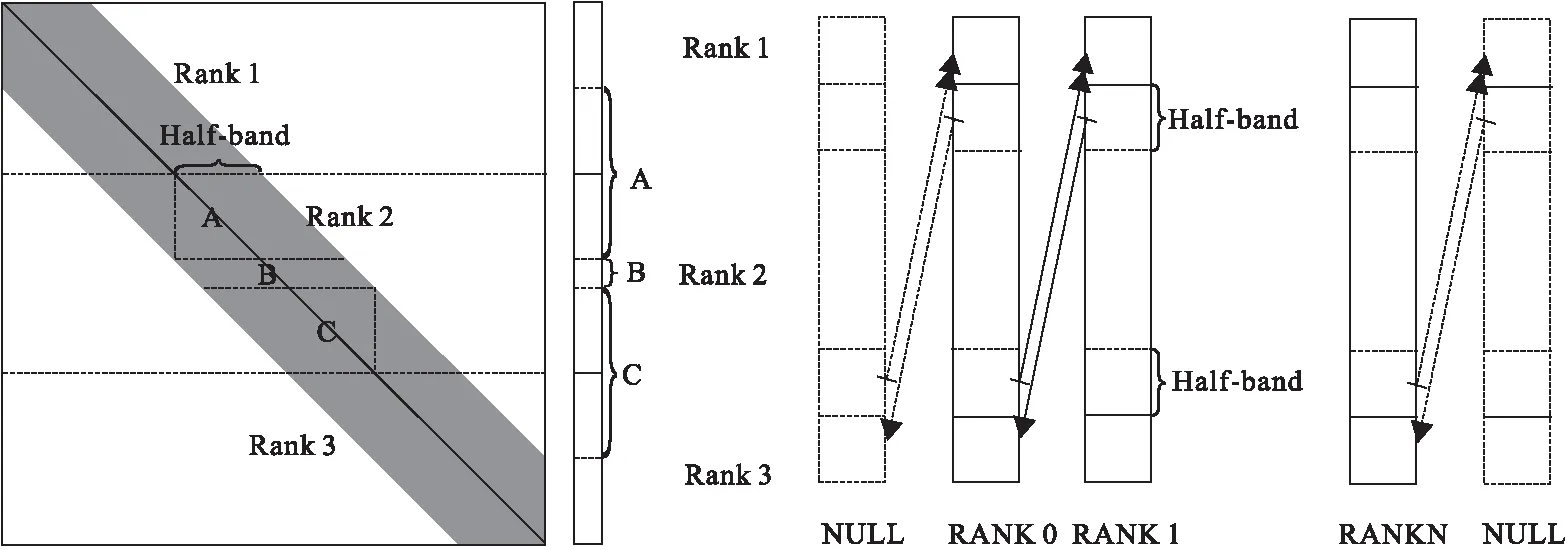
图3 矩阵行块划分及向量连续划分以及MPI通信示意图Fig.3 Partition of matrix and vector (left) anf data transmission in each node with MPI (right)

为了统一编程，在RANK0前面和RANKN后面分别添加一个MPI的虚拟进程NULL[18]。第一次通信：将自身前半个带宽向量通信到上一个秩向量列最后(矩阵第三块进行SpMV计算需要)；第二次通信：将自身后半个带宽向量通信到下一个秩列最前(矩阵第一块进行SpMV计算需要)。

4 实验结果

对三维直流电法模型研究区域使用TetGen[20]软件进行非结构化网格剖分，使用不同参数生成不同的网格数目进行测试。程序完全由FORTRAN和CUDA FORTRAN编写，实现了通用接口，可以方便地供现有FORTRAN程序调用。实验使用CentOS 6.5操作系统(CPU：Intel Xeon E5-2670 @ 2.60GHz)，GPU为NVIDIA Tesla K40c(2880 core@745MHz，Peak single precision floating point performance: 4.29 Tflops，Peak double precision floating point performance: 1.43 Tflops)，驱动版本为352.39 ，开发工具为CUDA Toolkit 7.5。实验中向量和稀疏矩阵运算调用NVIDIA函数库cuBLAS和cuSPARSE。GPU集群通信使用MVAPICH2-2.1配合Mellanox InfiniBand。编译使用PGI发布的支持CUDA FORTRAN的pgf90编译器。为保证计算精度，计算一律采用双精度浮点数和长整型整数。

图4 两层模型视电阻率计算结果Fig.4 Apparent resistivity of the two-layer model

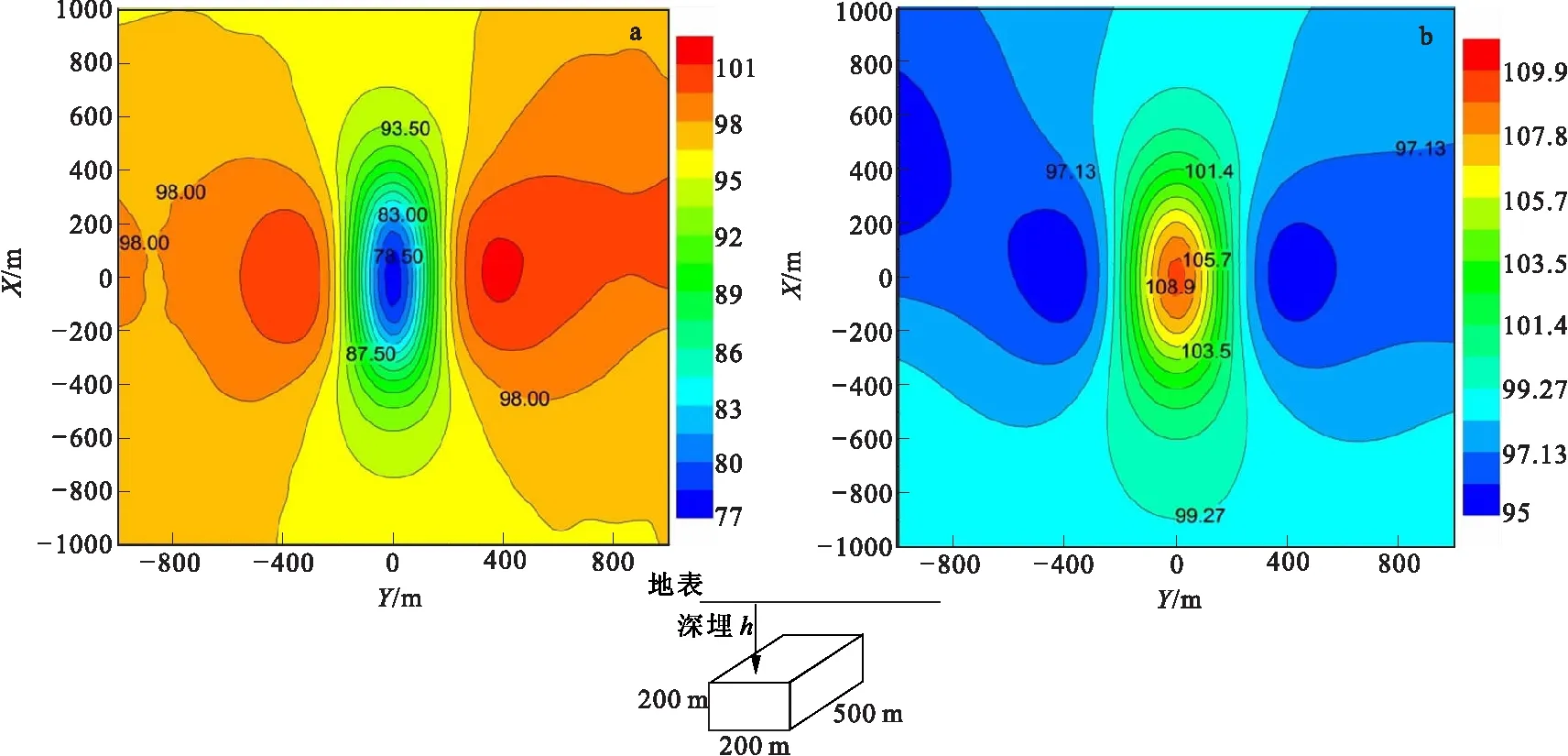
图5 低阻模型与高阻模型计算结果Fig.5 Results of the low resistivity model and the high resistivity model(a)低阻模型；(b)高阻模型

4.1 GPU计算结果及精度检验

为检验程序计算正确性和精度，本次实验设计了具有解析解的两层模型。取模型第一层电阻率为100 Ω·m ，层厚为 20 m ，第二层电阻率为10 Ω·m。点电源位于原点，电流强度为1 A ，限制迭代结束标志为 ‖Au-b‖/‖b‖ <10-10(所有计算均使用此收敛条件)。本程序计算的单极-单极视电阻率结果见图4。与解析解对比，靠近源数值计算误差较大，最大为3.39%，远离源误差不超过1.0%，计算视电阻率曲线与理论曲线趋势一致。

另外本程序计算两个典型的低阻和高阻模型(图5)，取供电电极AB=4 000 m，即A(0,2000,0)，B(0,2000,0)，埋深h=200 m。围岩电阻率为 100 Ω·m，低阻和高阻模型分别设置块体电阻率为 10 Ω·m 和1 000 Ω·m。地表四极观测的视电阻率如图5所示，可明显看出地下低阻体和高阻体的存在，视电阻率图对称性较好。从以上解析解对比及模型计算，可以看出本程序计算是正确可靠的。

4.2 多GPU扩展性研究

为研究GPU集群的扩展性，本次实验选用了不同大小的网格做测试(表2)。实验结果表明，在GPU上采用RCM排序后的SSORAI算法明显快于未排序的计算。原因是由于排序后，矩阵带宽明显减小，调用cuSPARSE库函数cusparseDcsrmv进行矩阵向量乘时，可以合并访存以及减少线程的分歧，进而减少计算时间。建议在非结构化网格剖分中，尽量使用带宽缩减算法减少带宽，以提高矩阵向量乘的性能。

表2 RCM排序后SSORAI-CG计算时间对比Tab.2 Time of SSORAI-CG algorithm with RCM sorting and without sorting

图6展示了笔者提出的方法对于大规模稀疏线性方程组的求解具有很好的扩展性。在较小矩阵规模时，由于通信占用时间较长，加速比较低；当矩阵规模增大时，加速比亦增大。在矩阵规模超过300×104时，2块GPU卡相对1块GPU卡有1.86倍的加速比，4块GPU卡相对于1块GPU卡有3.35倍加速比。本次试验中，最大矩阵维度约为900×104，此时2块GPU卡能能达到1.95倍加速比，4块GPU卡能达到3.76倍加速比，效果较为理想。

图6 GPU集群扩展性Fig.6 Expansibility of GPU clusters with our algorithm

5 总结

笔者采用SSORAI预处理共轭梯度法，求解直流电法正演生成的线性方程组，提高了预处理的并行性；该方法迭代次数较SSOR预处理略多，单次计算时间在小规模矩阵时较SSOR少；但随着矩阵规模增大，SpMV耗时增加，所以有使用多GPU加速的必要。

针对多GPU上负载均衡的问题，使用RCM算法进行矩阵重新排序，减少矩阵带宽，提高数据局部性。实验结果表明，RCM算法的时间与矩阵规模呈线性关系，耗时较少；同时，由于排序后矩阵数据局部性较好，计算的时间较未排序有明显地下降，随着矩阵规模增大能有1.6倍～3.9倍的加速。建议对于大带宽矩阵迭代求解时，先使用带宽缩减算法对矩阵进行带宽缩减，可以大幅提高计算性能。对排序后的矩阵采用矩阵行块划分，采用通信计算重叠，基于多GPU实现的预处理共轭梯度法获得了很好的加速比和可扩展性。基于2块GPU卡实现时，随着矩阵规模不同，能获得1.47～1.95的加速比；基于4块GPU卡实现时，在矩阵规模较小计算量较小时，通信所占比重较大，只能获得小于2倍的加速比，但随着矩阵规模增大，矩阵规模大于三百万时能获得3.35倍以上的加速比，本次实验中，在889×104规模时获得了3.76倍加速比。

致谢：

本论文的数值计算得到了中国科学技术大学超级计算中心的计算支持和帮助。

[1] 傅良魁.电法勘探教程[M]. 北京：地质出版社, 1983. FU L K, Electrical prospecting tutorials[M] . Beijing: Geological Publishing House, 1983. (In Chinese)

[2] WU XIAOPING. A 3-D finite-element algorithm for DC resistivity modeling using shifted incomplete cholesky conjugate gradient method[J]. Geophys. J. Int., 2003, 154 (3): 947-956.

[3] 王威, 吴小平. 电阻率任意各向异性三维有限元快速正演[J]. 地球物理学进展, 2010,25 (4): 1365-1371. WANG W, WU X P . Rapid finite element resistivity forward modeling for 3D arbitrary anisotropic structures[J]. Progress in Geophysics, 2010,25(4):1365-1371. (In Chinese)

[4] 吴小平.利用共扼梯度算法的电阻率三维有限元正演[J]. 地球物理学报, 2003，46(3):428-432. WU X P . A 3D finite element resistivity forward modeling using conjugate gradient algorithm[J]. Chinese Journal Geophysics, 2003,46(3): 428-432. (In Chinese)

[5] RUETSCH G, FATICA M. CUDA Fortran for scientists and engineers: best practices for efficient CUDA Fortran programming[M]. Elsevier, 2013.

[6]CUDA Fortran programming guide and reference,2016.[online]Available:https://www.pgroup.com/doc/pgicudaforug.pdf

[7] WANG H, POTLURI S, BUREDDY D, et al. GPU-aware MPI on RDMA-enabled clusters: Design, implementation and evaluation[J]. Parallel and Distributed Systems, IEEE Transactions on, 2014, 25(10): 2595-2605.

[8] LI R, SAAD Y. GPU-accelerated preconditioned iterative linear solvers[J]. The Journal of Supercomputing, 2013, 63(2): 443-466.

[9] GEORGESCU S, OKUDA H. Conjugate gradients on multiple GPUs[J]. International Journal for Numerical Methods in Fluids, 2010, 64(10‐12): 1254-1273.

[10]GRIEBEL M, ZASPEL P. A multi-GPU accelerated solver for the three-dimensional two-phase incompressible Navier-Stokes equations[J]. Computer Science-Research and Development, 2010, 25(1-2): 65-73.

[11]CEVAHIR A, NUKADA A, MATSUOKA S. Fast conjugate gradients with multiple GPUs[M]. Computational Science-ICCS. Springer Berlin Heidelberg, 2009.

[12]CEVAHIR A, NUKADA A, MATSUOKA S. High performance conjugate gradient solver on multi-GPU clusters using hypergraph partitioning[J]. Computer Science-Research and Development, 2010, 25(1-2): 83-91.

[13]赵莲, 赵永华, 陈尧, 等. GPU集群加速近似逆预条件CG并行求解器[J]. 计算机科学与探索, 2015, 9(9): 1084-1092. ZHAO L, ZHAO Y H, CHEN Y, et al. Approximate inverse preconditioned CG parallel solver on GPU cluster[J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(9): 1084-1092. (In Chinese)

[14]SAAD Y. Iterative methods for sparse linear systems[M]. Siam, 2003.

[15]HELFENSTEIN R, KOKO J. Parallel preconditioned conjugate gradient algorithm on GPU[J]. Journal of Computational and Applied Mathematics, 2012, 236(15): 3584-3590.

[16]GEORGE A, LIU J W. Computer solution of large sparse positive definite[M]. Prentice Hall Professional Technical Reference. 1981.

[17]陈国良. 并行计算: 结构· 算法· 编程[M]. 北京：高等教育出版社, 2011. CHEN G L. Parallel computing: structure, algorithm and programming [M]. Beijing: Higher Education Press, 2011. (In Chinese)

[18]都志辉, 李三立, 陈渝, 等. 高性能计算之并行编程技术--MPI 并行程序设计[M]. 北京: 清华大学出版社, 2001. DU Z H,LI S L,CHEN Y,et al. Parallel programming technology in highperformance computing- MPI parallel programming[M]. Beijing: Tsinghua University Press, 2001.(In Chinese)

[19]MVAPICH2: http://mvapich.cse.ohio-state.edu/

[20]TetGen: http://wias-berlin.de/software/tetgen/

[21] CUTHILL E, MCKEE J. Reducing the bandwidth of sparse symmetric matrices[C]. Proceedings of the 1969 24th national conference. ACM, 1969: 157-172.

[22] GIBBS N E, POOLE, JR W G, STOCKMEYER P K. An algorithm for reducing the bandwidth and profile of a sparse matrix[J]. SIAM Journal on Numerical Analysis, 1976, 13(2): 236-250.

[23]WANG W.,WU X.,SPITZER K. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids[J]. Geophys. J. Int,2013,193(2):734-746.