基于改进随机森林的洗钱交易角色识别应用
张 昊,黄 蔚,胡国超
(华北计算技术研究所,北京 100083)
0 引 言
洗钱犯罪严重破坏经济稳定,同时还为诸如毒品、恐怖活动犯罪、贪污腐败提供了便利,严重影响了社会稳定[1]。对于洗钱行为的发现一般流程是通过发现可疑交易,将可疑账号以及与该账号有交易关系的相关账号一并推送给公安机关进行立案分析,其中一个重要步骤是区分钱庄的经营账号以及与钱庄发生交易的客户账号。受限于信息化建设,对洗钱活动的线索挖掘仍处于人工判别的阶段。公安机关利用调查交易量较大的账户,通过审讯等手段进行分析。该方法大量依赖人力物力,分析周期长。
随着机器学习技术的发展,人们尝试在经济犯罪领域使用。这些研究多着眼于在大量交易中找出异常交易,但是对于找出的异常交易者进行身份判定的研究较少。近年来的研究包括Tang[2]提出的基于交易特征的交叉孤立点检测模型,李欣月等人[3]提出的基于CURE聚类算法的交易离群点识别。该类算法利用交易者的交易统计信息以及背景信息找出异于主体数据的个体以识别可疑交易。以上算法仅仅从交易统计的偏离度入手,并没有考虑到交易的时序性,也没有将与之交易的上下游纳入分析。张璐[4]利用小波分析,找出某个经济主体在时序上交易的突变,并利用突变的程度来判断是否涉及洗钱,但是在区分钱庄与客户时没有考虑交易网络结构,因此在实际使用中往往效果欠佳。
针对以往工作的不足,本文利用交易网络的拓扑特征,结合交易统计特点、交易特征的异常,从各个角度提取特征,设计一种基于随机森林的自动识别方法,并结合实际经验进行改进,得到一个有效的洗钱网络经营账户与客户账户判别的方法。
1 应用框架与关键特征
本文的主要处理对象为金融机构上报的可疑交易以及与该交易参与人有经济往来的一批经济主体的交易流水,并在此之上构建应用。依据经济学专家对洗钱行为的分析,交易主体的基础属性刻画了其身份背景,交易统计信息刻画了其交易习惯,交易偏离度刻画了其交易的异常程度,交易网络特征刻画了其在洗钱交易网络中的地位。以上4个方面都从一定角度反应了一个经济主体从事于洗钱犯罪中所处角色的可能性[4]。
本文从以上的各个角度提取出可以进行分类器训练的、有代表性的特征,并利用改进的随机森林算法在这些特征之上基于已有的数据训练出一个有效的分类模型。当模型训练完成后,通过对需要处理的同样类型数据经过相同的流程处理,就可以自动判别出这些参与洗钱者的身份。
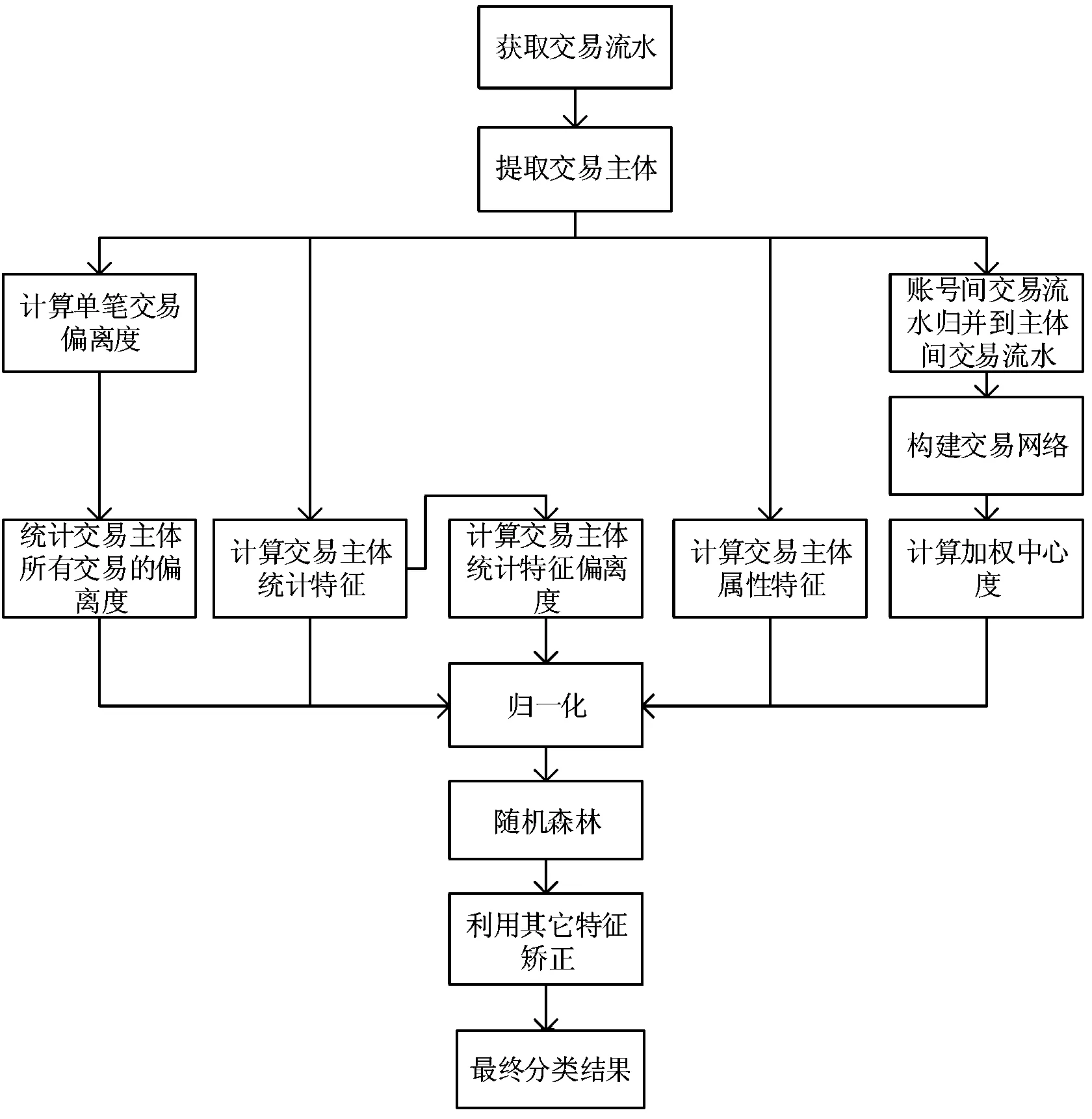
图1 角色识别流程图
1.1 属性特征
1.1.1 主体类别
根据银行账户的类别,经济主体可以是单一个体的自然人(或者是一个集体的公司)、组织机构,这两者一般在交易体量、其参数提取上有明显的区别,该特征用在决策树中可以让模型针对2种类别训练出不同的参数。该特征可以通过交易证件号码是否是身份证号,使用一个二值变量区分。
1.1.2 所在地
根据经验洗钱犯罪集团的成员往往有地域集中性[5],所以使用经济主体的籍贯有一定意义,一般认为沿海地区、经济发达地区更有从事洗钱的便利。籍贯地采自身份证前2位,而组织机构的交易所在地都是固定的,可以通过交易所在地按地域编码得到。
1.1.3 年龄
一般未成年人或是老年人参与洗钱犯罪的概率相对较低。年龄信息也可以从身份证号码中提取到。特征即是当前分析的时间减去出生年份得到。
1.2 交易的统计特征
数据的统计特征往往可以初步反映数据的分布情况,利用统计特征对一个经济主体的交易信息空间进行表示也可以大致描述该经济主体的交易模式。从某经济主体的一条交易记录提取出二元组(xi,ti),其中xi代表某次金额(收款为正,付款为负),t代表交易的时间。该经济主体的所有n次交易记录中的金额、时间可表示为(x1,t1),(x2,t2),…,(xn,tn),统计特征[5]计算方式如表1所示。
表1 统计特征

特征名称计算方式交易频率(tn-t1)/n交易次数n交易总额|x1|+|x2|+…+|xn|平均交易额(|x1|+|x2|+…+|xn|)/n交易留存率(x1+x2+…+xn)/n
同时,针对洗钱流转资金时常常使用外汇逃避金融机构的检测[7],外汇在交易中使用的占比也具有参考价值。
1.3 交易习惯的偏离度特征
洗钱交易一般与正常的交易有显著的区别,在所有的交易数据中,大量的交易都是正常交易,因此洗钱所产生的交易一般在整个交易中属于异常点[7]。钱庄经营账户由于大量参与洗钱交易,相比于客户账户这种偶尔参与的账户,交易行为会更加异常。
本文通过Isolation Forest算法[8]对偏离特征进行抽取。Isolation Forest用于挖掘异常数据,可以在包含所有样本的特征空间中找出空间中与大量数据距离较远的点[9]。该算法的空间、时间复杂度较低,在面对大量、复杂的交易数据时也可以快速有效地处理。
交易主体的异常程度可以从其交易统计值来刻画,同样也可以通过其每一笔交易的平均异常程度来刻画。
1.3.1 统计值异常度
交易主体偏离度依据交易的统计特征构成的特征空间来计算该经济主体的交易异常度。
1.3.2 单笔交易异常度均值
将每一笔交易的金额、双方交易地区域码等作为单笔交易的特征值,并在所有交易组成的数据集上计算交易的异常度,并以此计算某经济主体参与的所有交易异常度均值。
1.4 交易网络的中心度特征
交易网络是一个有向图,其中节点代表了一个交易主体,而2个交易主体之间的边则描述了这2个交易主体之间的交易行为,付款方以及收款方分别构成交易网络中的父节点与子节点。为了减少图的规模以及去掉干扰,需要对点的集合按照总交易次数、与边的集合按照单次交易金额进行筛选,并在成图之后剔除孤立点。对于被剔除的节点基本可以认为是非钱庄的经营者,其有网络计算得到的特征值可以由一个常数代替。
交易网络中边的权重可以从不同的角度进行度量:常数(单纯考虑由交易组成的关系网)、交易金额、交易次数、交易频率等。根据中心度的计算公式和代表意义,当图的权重不是常数时,边的权值越大则表明2点关系越紧密,这和中心度计算距离的方式相违背。所以本文在构建交易网络时对原有的权值W′为:
W′=1-ln (W)
(1)
其中W为原来的权值。
在图论与网络分析中,中心性(Centrality)是判定网络中节点重要性的指标,是节点重要性的量化。利用中心度,可以从网络结构入手分析网络中每个节点,对于网络的角色给定一个可以特征化的数值,从而丰富节点的特征信息。在刻画交易网络中,本文主要使用的中心性包括以下3种[10]。
1.4.1 点度中心度
如果一个账号与许多账号有交易关系,那么这个账号在整个交易网络中应该有更高的活跃度,理应受到更大的关注。点度中心度描绘了节点的出度、入度,认为一个节点如果有更多的节点与之相连,则认为这个节点在网络中更为重要[11]。
对于有N个节点的图G=(E,V),节点i∈V的点度中心度为:
Cd(i)=(deg (iin)+deg (iout))/(N-1)
(2)
其中deg(iin)为点i的入度,deg(iout)为点i的出度。
1.4.2 介数中心度
钱庄是整个网络的连接要点,处于钱庄资金流转的关键路径上。而这样的节点更多地出现在任意2个节点的最短路径上,因此引入介数中心度来衡量一个节点在这个网络中的重要程度[11]。介数中心度的核心是整个网络中的一个节点出现在任意2个节点的最短路径上的次数与所有最短路径的条数的占比。
在图G中,节点i的介数中心度为:
(3)
其中gjk为连接j,k两点最短路径的个数,gjk(i)为节点i位于最短路径的个数。
1.4.3 接近中心度
在交易网络中,钱庄账号节点的拓扑位置也具有一定价值,这里使用接近中心度来衡量一个账号的拓扑位置。接近中心度高的节点被认为更加处于网络的中心,因为它到其它节点的路径相对较短[11]。所以接近中心度核心是整个网络中的一个节点到其它节点的平均距离。在图G中,节点i的接近中心度为:
(4)
其中d(i,j)为节点i到节点j的最短路径长度。
1.4.4 交易主体的中心特征加权
在形成的交易网络中分别依据点定义计算出各个节点的中心度。根据实验,直接得到的中心度在区分部分特殊经济主体有欠缺,例如交易行为相对隐蔽的钱庄经营者或是交易相对频繁的企业账号,因此需要对中心度进行改进。中心度作为特征,其区分度没有足够显著的原因是中心度仅仅从交易网络的结构方面进行分析,而交易信息中还应该包含户主个人的历史交易流水信息。
在构建交易网络时分别使用了交易次数或是交易金额作为路径权值,所以本文提出使用路径权值外的另一个参数对中心度进行校正,即当使用交易次数作为路径权值时,将交易金额乘上中心度参数。将这个参数作为中心度的权值可以有效地抑制因其它原因与钱庄小额交易密切的正常账号或是不活跃的账户被识别成钱庄经营账户的概率,从而提升该参数对于特殊情况的区分能力。
1.5 参数归一化
为了提升模型的迁移能力,即是训练好分类器参数后的模型依旧适用于其它洗钱网络,需要对参与训练的非离散特征数值进行归一化处理。归一化后的特征值处理会将被线性地缩放到同一个度量尺度上[12]。
将以上计算得到的统计值、偏离度进行以下处理,得到归一化后的特征值λ′:
λ′=(λ-λmin)/(λmax-λmin)
(5)
其中λ为未经过归一化的原数值。
1.6 利用其它特征对特殊点进行校正
在试验过程中,发现部分识别错误的点有着与常识不符的特征,例如某个地下钱庄的经营者仅仅有数笔千余元的交易记录。对于这种情况,可以尝试利用交易记录中的其它信息对这类数据进行校正。
根据调查,地下钱庄一般呈现出家族性、区域性特点。对于未被随机森林判别成钱庄的,可以利用其交易记录中的交易方属性信息,与算法识别出的钱庄经营者的姓氏、身份证中的籍贯进行对比,如两者相同,则该户主与算法识别出的地下钱庄的经营者属于家族关系,同样有很大可能也是地下钱庄的经营者之一[5]。
2 改进的随机森林
随机森林具有较好的抗噪能力,针对洗钱交易规律复杂的特征有较好的预测能力,同时有特征选择能力,可以针对提出的各个特征的有效性进行验证,并且易于并行,适合处理大量数据[13]。
传统的随机森林[14]通过对输入的数据同时使用行采样与列采样。对于行采样,随机森林采用有放回的方式在N个样本中选取n个样本(n 为了提升随机森林在此应用中的准确率,特别是对钱庄经营者的识别率,本文对传统随机森林进行了改进。 考虑到各类数据样本数量不平衡,所以在训练决策树时引入虚拟少类向上采样(SMOTE)技术[15]。SMOTE通过在特征空间中,人工地在少数类样本点附近构建新的少数类样本,从而增加少数类样本数量,减少数据不平衡。 SMOTE的算法流程包括3个步骤:1)对于少数类的每一个样本x,选取距离最近的k个少数类样本;2)随机从k个邻近样本中选取一个,记为xi;3)新的样本xnew=x+rand(0,1)×x。 通过SMOTE技术扩充钱庄经营者的样本数量后再进行随机森林的训练,可以降低钱庄经营者数量远远小于客户的问题。 为了保证训练集与OOB中同时有2类样本,采样时分别从2类样本集合中以同样的概率进行采样,否则训练集有更大的概率采样到非钱庄样本,避免训练集对非钱庄经营者更加敏感而难以识别钱庄经营者。 当一棵决策树建立好之后,可以利用OOB数据对当前的决策树进行评估,从而给出这颗决策树在特定领域下的适应性。 传统的随机森林中每一棵决策树都有相同的投票权,参考高元等人[16]利用OOB数据提高随机森林的性能,在此对决策数的预测结果引入一个权值[17]。 因为该模型的重点在于找出钱庄的经营者,因此使用该决策树对OOB中钱庄经营者的识别率来衡量这棵决策树在森林中的重要程度。 设OOBi,j代表建立的第i棵决策树Treei时OOB中类别为j∈{钱庄经营者,钱庄客户}的样本集合,Treei对于样本x预测结果记为Pr ei,x。则定义OOB中钱庄经营者的识别率P为: (6) 其中I为指示函数。 当每棵决策树根据公式(6)计算出重要度后,依据归一化后的重要度作为每棵树投票的权重。 利用公安提供的几组实际洗钱案件交易数据,将以上得到的4类描述经济主体的特征值依照相同的顺序组成特征向量,所有涉及的经济主体的特征向量组成样本空间。利用查获的钱庄账户对每个样例进行标记。每次实验选取其中的一组数据作为训练集,另外的几组数据作为测试集。将账户在钱庄账户中的标签置为1,否则置为0。将所有样本的特征向量组成特征矩阵依据改进的随机森林模型进行训练。 所有经济主体上统计交易记录中的收付款次数、金额、留存、平均单次交易金额,结果如表2、表3所示。 表2 钱庄经营交易统计 统计值付款次数/次收款次数/次付款总额/万元收款总额/万元留存金额/万元平均金额/元均值1456.501155.0046.4835.53-10.94678.23方差1418.431115.5149.5847.4854.02698.22 表3 户交易统计 统计值付款次数/次收款次数/次付款总额/万元收款总额/万元留存金额/万元平均金额/元均值528.85454.7056.8345.51-11.315792.32方差1451.651223.6649.5861.2054.028733.29 传统的统计信息在2组账户之间有一定的差别,但是2组的统计值的方差都很大,数值交杂在一起,难以单独作为2种账户的判别标准。 首先利用实验数据构建交易网络。从实验样例中随机抽取20个钱庄经营账户以及20个客户账户,在构建的交易网络中计算以上40个样例的中心度,结果如图2所示,其中0~19号为经营账户,20~39号为客户账户。 图2 经济实体交易中心度特征 在所有交易记录中统计出这些账户的交易总额以及交易次数,按照计算其可疑度,作为各个中心度的权值。 图3 2组经济实体交易带权中心度特征 从上面的2个图中可以看出,经营账户的中心度在一定程度上比客户账户有更大的数值,但是其中仍然存在一些异常点,例如第1个、第6个、第9个钱庄经营账户的中心度较低,而第28个客户账户的中心度较高。 在引入可疑度作为中心度的权值后,大部分的经营账户与客户账户之间的数值差异进一步放大,可见加权后的中心度可以较好地作为经营账户的识别标志之一。 计算所有经济主体的统计信息构成特征空间,计算2组账号的偏离度,结果如表4所示。 表4 交易偏离度 统计值客户经营者平均值0.9259164.845249方差5.7523984.158647 从表4的结果可以看出,2组账号的偏离度具有不同的分布区间,钱庄账号的偏离度明显大于客户账户的偏离度。 3.4.1 特征贡献度 利用随机森林对特征的贡献度评估能力,在多个数据集合上经过多次实验得到各个类别特征的平均贡献度,如图4所示。 图4 4类特征的贡献度 从特征贡献度可以看出特征对分类结果都有一定贡献,特征之间关联较小。 3.4.2 分类性能分析 经过多次实验后得到分类的平均准确度、召回率、F1-score如表5所示。 表5 模型效果 准确度/%召回率/%F1⁃score/%93.8781.7287.37 3.4.3 与其它算法的对比 表6 效果比较 算法名称准确度/%召回率/%F1⁃score/%改进RF93.8781.7287.37RF91.2371.3580.07SVM89.7935.5650.94CURE聚类89.4365.3375.50 从表6的结果可以看出,在本文提出的特征集上使用随机森林模型进行分类预测有一定效果,特别是钱庄识别率均超过80%,使得该模型有投入实际使用的价值。特别地,对于CURE聚类算法不能找出的钱庄,因为其处于交易网络的中心,本应用也可以有效地发现。并且相比于传统的随机森林算法,改进的随机森林不仅对钱庄的识别率更高,还更加稳定。而常用的SVM算法对不平衡问题的适应性较差。基于CURE聚类的算法对差异明显的钱庄可以稳定识别,但是会将企业大量交易的账户也分到钱庄中,而钱庄中交易量相对较小的却不能识别出来。 本文依据公安现有办案的需求以及办案流程,通过提取交易数据中经济实体的属性特征、交易的统计特征、交易网络中的中心度特征、交易的偏离度特征,针对应用要求以及数据不平衡特点对随机森林算法进行了改进,并以此对可疑交易参与者的身份进行了分类,实验表明本文方法有一定的效果。 在实际办案过程中,本文方法用在实验的数据集不仅可以描述一个经济主体,而且利用该经济主体的身份证号码还可以利用其它数据对特征进行拓展。例如通过户口可以知道嫌疑人的现居住地址、社会经历、犯罪前科等信息。这些信息显然对判断一个经济主体是否涉嫌洗钱犯罪有着重要作用。 同时,随机森林算法有易于并行的优点,将本应用嵌入公安的研判系统中则必定会对实时性有要求,通过将随机森林算法的并行化以及使用图数据库进行图相关运算,则可以更大程度提升公安办案效率。 [1] 李云飞. 洗钱危害的二维性及对客体归类的影响[J]. 中国刑事法杂志, 2013,11(11):41-48. [2] Tang Jun. A cross datasets referring outlier detection model applied to suspicious financial transaction discrimination[C]// Lecture Notes in Computer Science. 2006,3917:58-65. [3] 李欣月,张高煜,彭兰舒,等. 基于聚类算法的金融交易离群点识别[J]. 电子技术, 2016(1):24-28. [4] 张璐. 数据挖掘技术在识别可疑金融交易中的应用[J]. 中文信息, 2015(1):73,291. [5] 李果仁. 反洗钱的现状与对策研究[J]. 广东经济管理学院学报, 2004,19(1):71-76. [6] 丁韶年,汪革清. 电子商务信用风险和特征分析[J]. 电子商务世界, 2004(5):72-73. [7] Alexander K. The International anti-money-laundering regime: The role of the financial action task force[J]. Journal of Money Laundering Control, 2001,7(3):195-196. [8] Liu F T, Ting Kaiming, Zhou Zhihua. Isolation-based anomaly detection[J]. ACM Transactions on Knowledge Discovery from Data, 2012,6(1):1-39. [9] 侯泳旭,段磊,秦江龙,等. 基于Isolation Forest的并行化异常探测设计[J]. 计算机工程与科学, 2017,39(2):236-244. [10] 付立东. 复杂网络中心性度量及社团检测算法研究[D]. 西安:西安电子科技大学, 2012. [11] Brandes U, Borgatti S P, Freeman L C. Maintaining the duality of closeness and betweenness centrality ☆[J]. Social Networks, 2016,44:153-159. [12] 杨慧中,卢鹏飞,张素贞,等. 网络泛化能力与随机扩展训练集[J]. 控制理论与应用, 2002,19(6):963-966. [13] Breiman L. Random forests[J]. Machine Learning, 2001,45(1):5-32. [14] 林成德,彭国兰. 随机森林在企业信用评估指标体系确定中的应用[J]. 厦门大学学报(自然版), 2007,46(2):199-203. [15] 王仁东. 基于数据挖掘技术的反洗钱监测研究[D]. 哈尔滨:哈尔滨工程大学, 2013. [16] 高元,刘柏嵩. 基于集成学习的标题分类算法研究[J]. 计算机应用研究, 2017,34(4):1004-1007. [17] 周浩. 基于随机森林的代价敏感特征选择研究[D]. 厦门:厦门大学, 2015.2.1 样本采样
2.2 利用OOB对建立的决策树加权
3 实验结果
3.1 统计信息分析
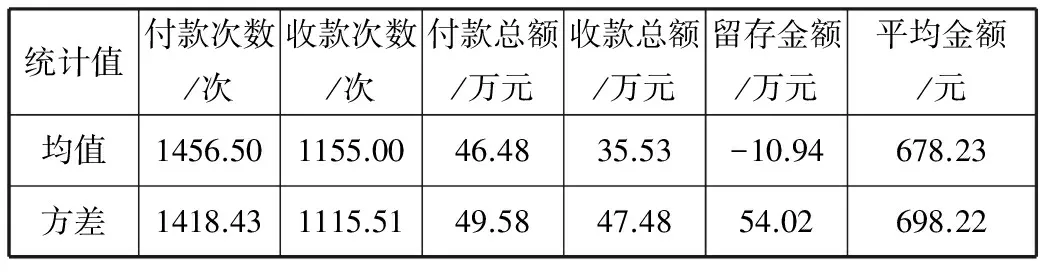
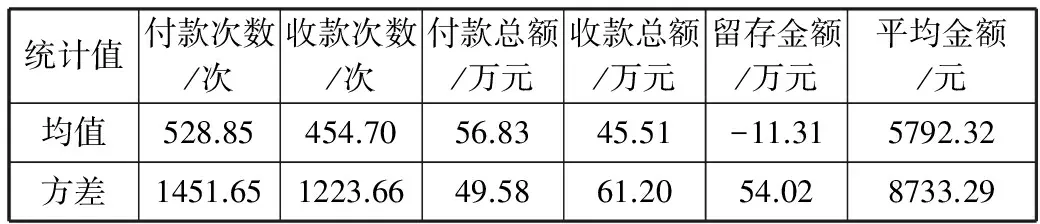
3.2 中心度以及加权中心度分析
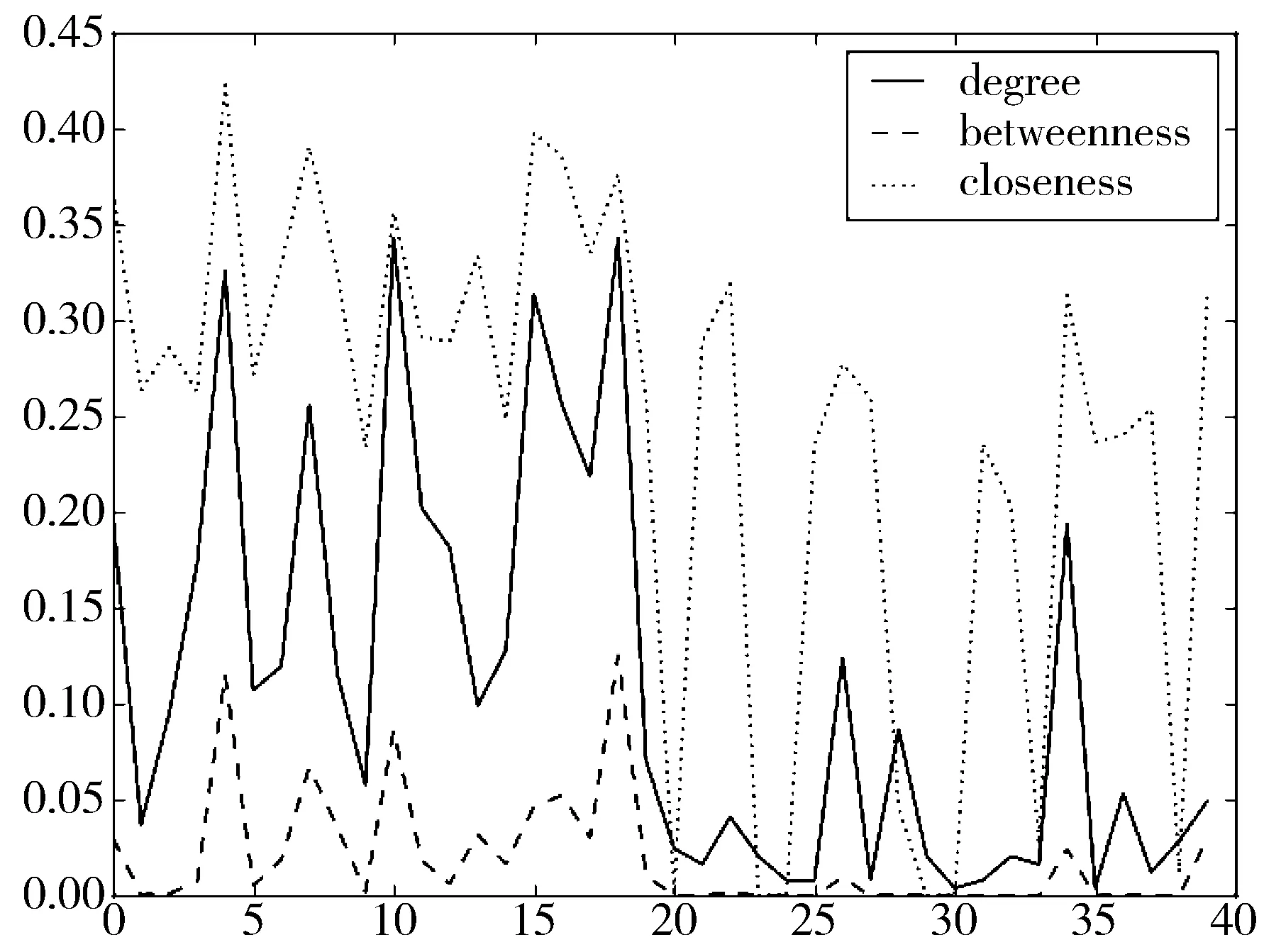
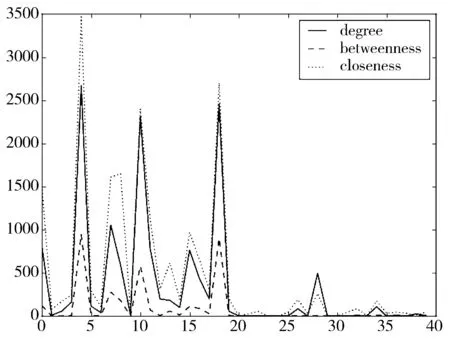
3.3 偏离度分析

3.4 分类结果分析
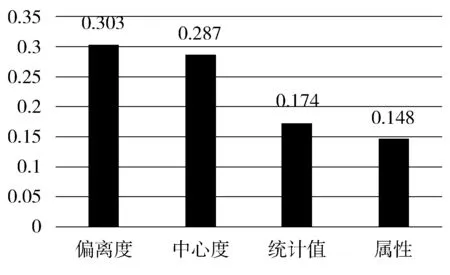

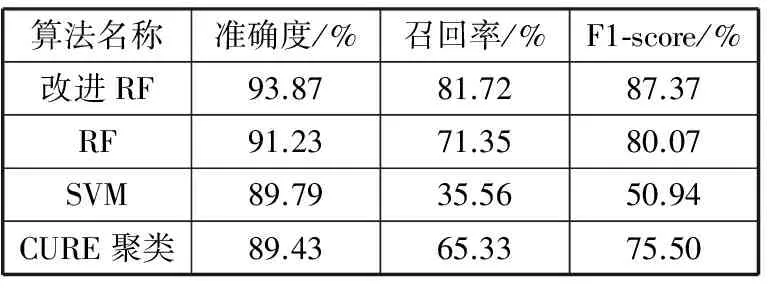
4 结束语

