一种基于策略集的概率缩域算法对多目标随机组卷问题的解决方案
周华君,丁爱芬,吕小俊
(云南大学旅游文化学院,云南 丽江 674100)
0 引 言
随着高校信息化教学的推进,电子考试系统在高校教考过程的展开,自动组卷是电子考试系统中一个非常重要的组成部分,保证自动组卷的科学性、随机性和高效性是自动组卷算法研究的一个难点[1-2]。当前自动组卷算法在研究组卷的随机性上基本采用随机洗牌算法[3-5]和模拟退火算法[6-8],随机洗牌算法在选题过程中较快,但是选择方法较单一,错误率较高;模拟退火算法本质上也是一种随机算法,其在局部上作出了优化改进,但仍然无法满足组卷整体上的科学性。在研究组卷的科学性方面(如满足试题的区分度、重复率、难易度比例、知识点分布)主要采用遗传算法[7,9-13]、回溯算法[2]。遗传算法在自动组卷的科学性主要体现为优秀遗传因子可以得到重用,即优秀试题组合可以得到重用,但无法满足题库抽取的随机性,且遗传算法的时间复杂性为O(2n);回溯算法遍历空间解的时间复杂度为O(n!),算法难度大,适合小题量的组卷。可以看出单一的组卷算法在保证组卷的科学性、随机性和高效性上都难以做到均衡。
自动组卷算法的随机性和高效性是基本要求。组卷算法的科学性是最终目标,组卷算法的科学性和高效性兼顾是难点。然而由于科学性的评定标准多样,通过制定构成组卷题目的知识点分布函数,对目标集重复使用随机算法和轮转均衡策略,可以有效保证组卷质量达到目标要求,满足了组卷的科学性;在组卷的随机抽取和轮转均衡过程中及时运用剪枝策略,缩小题库范围,提高组卷效率,二者结合能够有效满足组卷算法的科学性和高效性。
本文提出一种基于策略集的概率缩域算法,实现对多目标随机组卷问题的解决。首先通过对同组试题数据运用洗牌算法进行随机化,构成试题结果取值域,满足试卷抽取的随机性要求;其次通过构造满足用户需求的试题数据分布函数,实现对试题数据的均衡性选取;再次在选取过程中通过策略集对取值域进行提前剪枝,通过一定的概率密度,不断缩小取值域,直到结果集返回,满足组卷的高效率要求;最后对结果集进行均衡性量化,以一定的深度权重进行结果集的均衡化轮转处理[5],使抽取试卷的质量满足用户自定义策略要求,该算法的时间复杂性对试题数量的变化增量较小,适用于大规模题目的组卷工作。该算法与组卷份数存在着显著相关性,实验拟合结果符合二次曲线,即算法复杂度为O(n2),在试题数量为100000个、组卷份数为1000份的条件下,耗时仅为127 s,符合现代较大规模(题库量单位以万计)题库的自动组卷时效性要求。
1 组卷工作的基本模型
1.1 数据结构的基本定义
定义1试题题目结构定义为:
Q=
其中qid代表题目编号,qscore代表题目分值,qzid代表题目章节,qfacility代表题目难度,qfrequency代表题目抽取频度,dkeyword代表题目关键字。
定义2题型结构定义为:
T={txId,txScore,tmSize,tmList}
其中txId代表题型编号,txScore代表本题型构成分数,tmSize代表本题型所需题目数量,tmList代表本题型已选择题目队列。题目队列tmList={Qi},其中i属于N。
定义3试卷结构定义为:
E={eid,escore,Tlist}
其中Tlist={Ti}。
定义4题目库定义为:
tk={Qi},其中i属于N。将题目库划分为选中集TKchoose,待选集TKrest,剪枝集TKleft。
定义5策略结构定义为:
S={W,F1(TKchoose,TKrest,TkDelete,depth),F2(TKchoose,TKrest,TkDelete,depth),F3(TKchoose,TKrest,TkDelete,depth)}
其中W为策略权重,TKchoose为选中集和,TKrest为剩余集和,TKDelete为被剪枝集和,depth为回溯深度。F1,F2,F3为以depth深度对TKchoose,TKrest,TkDelete采用一定的策略进行选取、剪枝和调整操作。
定义6策略结合定义为:
Seqs={Si}
其中i属于N,Si代表单个策略。
1.2 概率分布密度函数的离散化
对任意概率密度函数Y=F(x)在x(a b)之内进行均匀取值,其中a,b分别对应试题某一属性的最小值和最大值,根据试题属性区间逐个取x得出Y对应的分布权重,通过权重需求构造分布区间,使抽取时按照该分布进行试题的抽取,满足试题抽取的策略性,具体构造算法过程如下:
1)通过SQL的Select distinct命令获取属性区间list,将list中最小值和最大值分别复制给min,max。
2)计算list各元素的最小间距l。
3)以l为距离单位,构造min,max间序列x1…xi…xn。
4)序列x1…xi…xn映射到a,b密度范围,分别求解对应密度序列y1…yi…yn。
5)yi即为任意分布函数对应的离散化密度序列。
2 组卷过程
2.1 试题自定义分布处理方法
1)如果是连续性分布,执行连续概率分布的离散化处理。
3)分布同样大小的数组Array。
4)填写yi个xi到数组Array。
5)对Array运用随机洗牌算法。
6)将洗牌后的Array加入指定策略集,等待策略集进行数据选取。
2.2 基本缩域算法
1)查询数据库获取组卷题目库,将试题取值域加入列表LinkedList
2)对mTiKuList进行快速排序,运用二叉排序树按分值大小进行降序排列,定义回溯深度depth。
3)初始化TKchoose为空,TKrest为全集,TkDelete为空。
4)定义组卷剩余分值restScore为题型分数txScore。
5)当restScore>0且TKrest.size()>0,则执行6)否则执行10),表明本试题分值不够且还有待选集。
6)应用策略函数在剩余集里随机取一个题目项tmp。
7)当tmp.getTimuscore()≤restScore,表明选中题目项的分值小于或等于剩余分值。
8)执行剩余分值调整,剩余分值=剩余分值-选择题目项分值。将题目项加入TKchoose,并从TKrest删除题目项。执行5)。
9)应用策略函数对TKrest执行一次剪枝,缩小选择域,将剪枝题目项放入TkDelete,执行5)。
10)判定题目数量TKrest.size()是否为0,如果是则执行11),否则,depth=depth-1。
11)判定回溯深度是否为0,如果是则返回false,否则执行3)。表明进行下一次的试探抽取,否则应用策略函数进行试题平衡化处理。平衡成功返回true,否则返回false。
2.3 基本剪枝策略
基本剪枝策略分为2种,一种是对试题抽取过程的尽快返回,一种是对选择区域的尽快缩小。
对试题抽取过程的尽快返回条件包括但不限于以下条件:
1)已抽取分值+剩余分值<题型需求分值;
2)已抽取试题个数+剩余试题个数<题型需求个数;
3)剩余题目不满足策略函数需求;
4)当前的剩余试题集不满足分布需求抽取要求。
对试题抽取域的缩小包括但不限于以下条件:
1)当前题目分值大于restScore,可以剔除待选序列;
2)当前策略集和已经满足,剩余满足的选项可以剔除待选序列。
通过定义策略集列表和策略处理响应逻辑,能够更快地实施对试题组的深度剪枝,加快算法对较大题库的快速求解,同时能够实现对算法处理过程的扩展。
2.4 自定义深度的均衡化轮转处理
均衡化轮转分为题型的选中题目个数与题型需求一致和不一致2种情形。一般先将不一致调整为一致,再进行后续调整,试题个数一致性调整过程如下:
1)定义测试深度outsizedeep。
2)当T.tmSize 3)开始合并,当TKrest.size≥2且outsizedeep>0则执行4),否则返回false。false代表本次调整失败。 4)在TKchoose集和的前1/2片段随机抽取题目A,B。 5)在TkDelete应用策略集抽取题目C,满足C.qscore=A.qscore+B.qscore;抽取到则执行6),否则outsizedeep=outsizedeep-1,执行3)。 6)在TKchoose集和中删除A,B,添加C。 7)开始分解,从TKchoose中随机选择A。 8)应用策略集在TkDelete和TKrest中找到题目B,C,满足A.qscore=B.qscore+C.qscore;否则outsizedeep=outsizedeep-1,执行3)。 9)从TKChoose中删除A,添加B,C;并从TkDelete和TKrest中删除B,C,执行3)。 在处理器为Intel(R) Core(TM) i7-4770CPU@3.40 GHz,内存为8 GB的Windows7 64位系统下,试题项的组成为每个试题的分值不超过20分,试卷分值为100分,每份试卷题目组题数为20个。使用Eclipse开发环境和Java语言,内存限制为500 MB,组卷份数以10为间距,题库题目数量以100为间距运行算法。实现结果如表1所示。 表1 不同题量与组卷份数耗时对比(ms) 抽取题目数量/道生成试卷份数/份14015016017018019020010057596472838383200313843465054593006470796274788540069769010110912313250070829410011312613560073809210611312413570072819310311112514180076849510411812914090079891011131191381451000829010211512413014711008997107117130138157120094104113125140161159130097106120131142154162140098109123131141157171150011611513614014816517416001081181281401551661821700113126137149163178190180011913113915416818419119001261361521651731912172000146161169181198208232 在题库题目数2000,抽取200份试卷的计算机耗时仅有230 ms左右,在本算法下,题库题目数量对组卷耗时的影响因子较小,相关因子为0.407,组卷份数对算法耗时影响较大,相关因子为0.861。 对组卷时间与组卷份数作回归分析,其二次、三次、复合函数描述散点图如图1所示。 图1 回归分析描述散点图 注:在题目量相同的情况下,v2代表组卷份数(份),v3代表消耗时间(ms),实线代表二次和三次曲线(两类曲线重合,根据调整后的R方的值,这里选择二次曲线),虚线代表复合曲线。 如图1所示,算法的组卷时间与组卷份数的变化趋势符合二次、三次曲线。结合调整后的R和方差检验,二次曲线更符合数据拟合要求。即算法效率与组卷份数呈现二次函数的变化趋势。算法效率与题库题目数量的变化较小,表明算法在题库题目数量增加较多的情况下变化不显著,算法适合较大题库的组卷要求。在增加内存为1 GB,题库量为100000个,组卷份数为1000份情况下,算法耗时为127 s。所以,基于策略集的概率缩域算法在解决多目标随机组卷问题上是可行的,能够同时满足时效性、均衡性要求。 本文提出了一种基于策略集的概率缩域算法对多目标组卷问题的解决方案。通过应用随机洗牌算法实现对试题数据选取的随机性,保证了试题抽取的随机性和均衡性;使用策略集实现对随机抽题的题项限定,达到试题选取符合用户指定分布的目标;运用策略集对目标待选集进行快速缩域,保证了算法执行的效率;运用策略集对结果进行轮转调整,既简化了试题组合效率,又使最终结果符合用户目标策略需求。最后以较大的题目量和一定的组卷步长,运用基于策略集的概率缩域算法检验抽题效率,实验结果符合较大规模题目的组卷实时性需求。 实验结果表明算法效率与组卷份数呈现二次函数的变化趋势,算法效率随题库题目数量的变化较小。即算法对组卷份数的时间复杂程度为O(n2);题库题目数量对组卷效率影响较小,算法适合较大题目量的组卷应用。由于算法的解决问题情景同样也可以应用于多目标的整数规划,研究多目标整数规划的快速解决方案是该算法的一般性应用研究方向。 [1] 袁桂霞. 自动组卷的建模和仿真研究[J]. 计算机仿真, 2011,28(11):370-373. [2] 高兴媛,古辉. 在线考试系统自动组卷技术的研究与实现[J]. 计算机与现代化, 2011(3):156-158. [3] 曹树国. 基于洗牌算法的快速个性化组卷方法的研究[J]. 计算机与信息技术, 2007(10):71-72. [4] 徐波,胡玉涛. 医药考试系统A1及A2题型的随机组卷算法研究[J]. 计算机与网络, 2016,42(21):63-65. [5] 魏波,喻飞,徐星,等. 基于改进轮盘赌策略的交互式演化算法[J]. 计算机与数字工程, 2014,42(10):1763-1767. [6] 吴焕,张琪君. 基于遗传退火算法的智能组卷系统研究[J]. 工业控制计算机, 2017,30(1):112-113. [7] 张辰,张艳群. 基于遗传和模拟退火算法的自动组卷系统设计与实现[J]. 计算机工程与科学, 2004,26(11):65-68. [8] 吴焕.张琪君. 基于遗传退火算法的智能组卷系统研究[J]. 工业控制计算机, 2017,30(1);112-113. [9] 张琨,杨会菊,宋继红,等. 基于遗传算法的自动组卷系统的设计与实现[J]. 计算机工程与科学, 2012,34(5):178-183. [10] 冯阿芳. 基于遗传算法的自动组卷策略[J]. 哈尔滨师范大学自然科学学报, 2008,24(4):27-30. [11] 吴飞. 自适应遗传算法解决组卷问题的探讨[J]. 重庆科技学院学报(自然科学版), 2007,9(2):132-135. [12] 许永达. 基于改进遗传算法的智能组卷研究[J]. 计算机与数字工程, 2013,41(2):176-178. [13] 薛方,苏虞磊. 基于改进遗传算法的试卷生成算法研究[J]. 现代电子技术, 2010,33(6):143-144. [14] 贺荣,陈爽. 在线组卷策略的研究与设计[J]. 计算机工程与设计, 2011,32(6):2183-2186. [15] 周艳聪,刘艳柳. 遗传模拟退火智能组卷策略研究[J]]. 计算机工程与设计, 2011,32(3):1066-1069. [16] 唐朝舜,董玉德. 在线随机组卷算法研究及实现[J]. 合肥工业大学学报(自然科学版), 2006,29(3):296-299. [17] 王晓东. 算法设计与分析[M]. 北京:清华大学出版社, 2010:195-273. [18] 余颖,李晓昀,左贵启,等. 基于自适应遗传算法的自动组卷策略研究[J]. 南华大学学报(自然科学版), 2016,30(3):61-65. [19] 顾玮. 遗传算法在试题自动组卷中的应用[J]. 办公自动化, 2016,21(18):57-58.3 实 验
3.1 实验条件
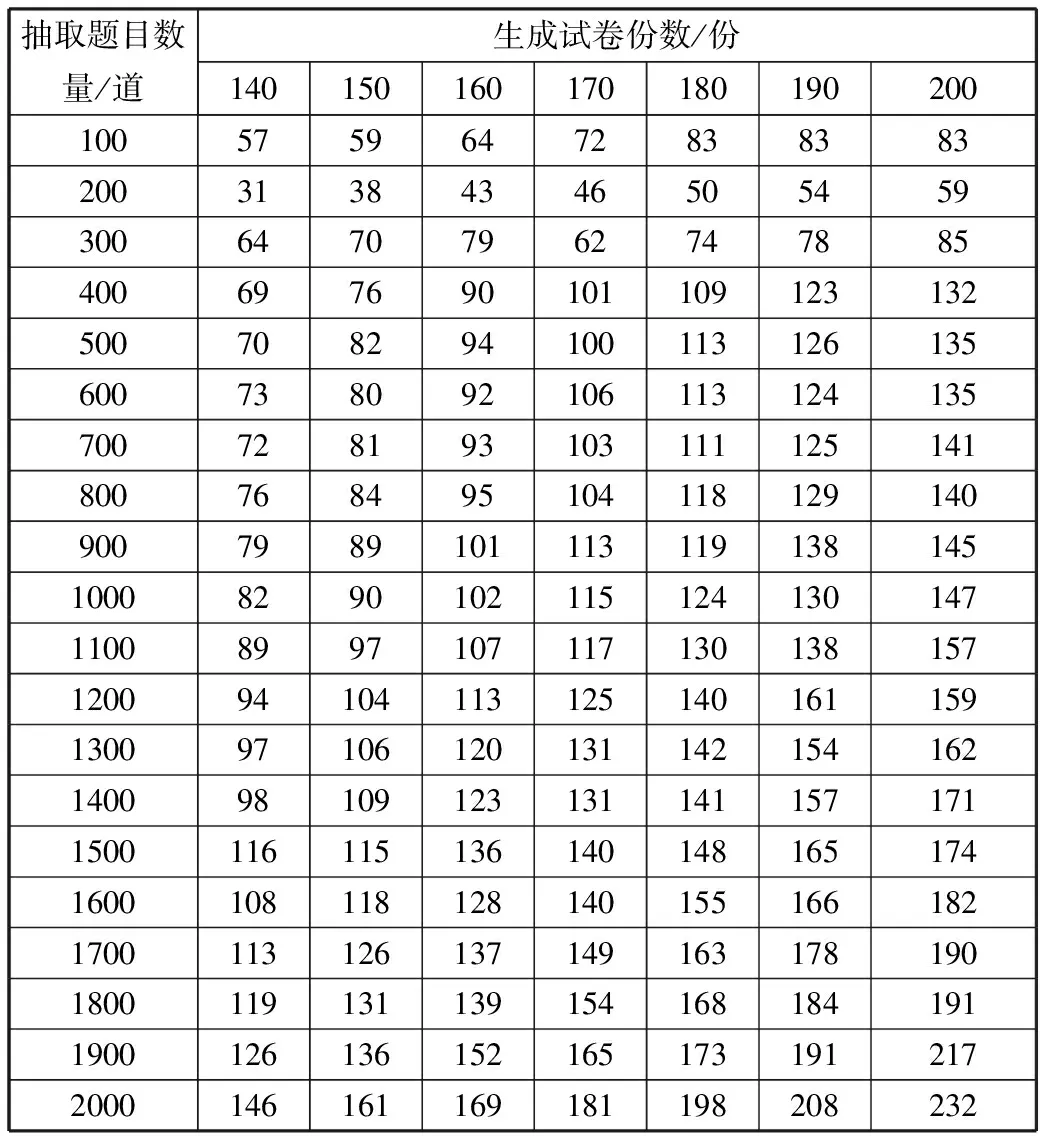
3.2 实验结果分析
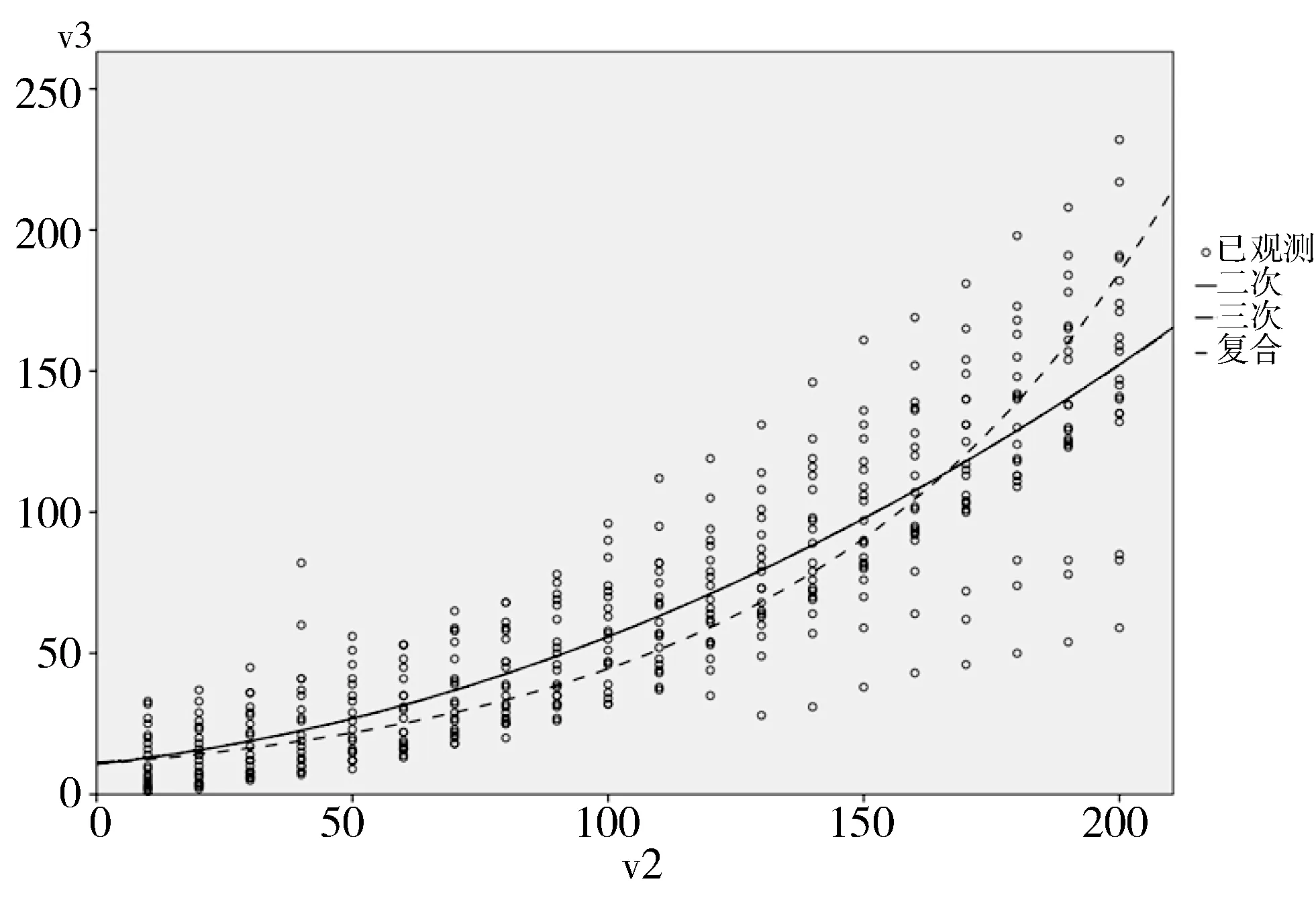
4 结束语

