改进FP-Growth算法在旅游线路规划中的应用研究

字云飞,李业丽,孙华艳,张莉婧

(北京印刷学院信息工程学院,北京 102600)

0 引 言

在物质生活不断提高的同时，人们对于精神享受的追求也更迫切了，旅行成为了人们追求高质量生活方式的最直接表达。大数据表明2016年国内旅游人数超过40亿，这一庞大的数据使旅游成为部分地方的支柱产业。但不管是旅游管理者还是旅行者，在充分利用资源的情况下制定旅游规划和选择旅行线路，并使自身利益最大化成为了当前最大的问题。当前的旅游市场主要是以传统的主题、超市、运筹学和市场导向为中心的线路规划，并没有利用信息技术革命中大数据挖掘和分析带来的优势，这在旅游线路规划中会造成一些不必要的损失。信息革命不断发展，人类进入工智能(AI)时代，大数据、数据挖掘及数据分析成为了智能旅游推荐系统的核心技术，同时得到了广泛应用。因此，通过对关联规则挖掘技术FP-tree算法的改进，应用挖掘的大数据进行分析和处理帮助旅游管理者和旅客规划出高效、科学及最大效益化的决策，这得到了旅游市场的强烈推荐。

1 FP-Growth算法及其改进

Agrawal等人提出的关联规则[1]挖掘技术Apriori算法[2]的缺点是对原始数据库多次重复遍历而产生大量候选集。针对Apriori算法的这一缺陷，Han等提出了通过树形结构来存储数据并进行频繁模式挖掘的算法—FP-tree算法。FP-tree算法是通过类似于数据结构中的树形结构来存储原始数据库的核心信息，采用逆寻方式来挖掘频繁项集，此算法只需对原数据库二次扫描且避免了产生大量候选项集。实验分析表明Apriori算法的性能比FP-tree算法慢一个数量级。虽然这2种算法的主要目的都是从数据库中挖掘出频繁项集，然而两者算法面对存有海量数据的数据库且支持度较小时，使用它们都是不现实的[3-6]。通过FP-Growth算法挖掘频繁项集时，不仅要多次递归条件模式树，且对树结构挖掘处理中会生成庞大的子集群，这会开销掉大量存储空间，使挖掘效率较低，并且需要占用大量的存储空间和多次递归建立条件模式树。本文将FP-tree树形条件模式库通过数据结构中的2个一维数组来存储[7-8]，极大减小了树形结构的存储开销，又通过FP-tree算法对节点进行预剪枝，可以减少对建立条件模式树和遍历子集次数，这对于算法挖掘数据的执行效率有极大提高[9-10]。

FP-Growth算法[11]的执行有2个核心过程：对于FP-tree算法的建树以及对树的逆寻递归挖掘。算法通过对原数据库的二次遍历，将这些数据存储在树结构的节点上，从而构建FP-tree前缀树，这也表明通过逆寻过程中前缀路径名共享实现了对数据的压缩。对已构建好的FP-tree树逆寻每个项的条件FP-tree、条件模式基以及通过遍历递归挖掘得到支持度-置信度模式的所有频繁项集。

本文将条件模式库通过数据结构的2个一维数组存放FP-tree树的节点信息，分别为支持度数组和索引数组作为改进。如频繁1项集L={I1,I2,…,In}，则支持度数组和索引数组长度等于n，数组下标从1开始，第0号另用。下面为构建FP-tree的过程：

首先，对1项集的求解。先将支持度数组设为0，然后通过逆寻遍历所寻项路径分支，分支各节点对应的位置进行支持度累加，扫描完所有分支后，在支持度数组中记录各节点的支持度，存储树节点的支持度。

其次，对于索引数组的处理。对每个节点不小于设置的支持度阈值的值从高到低有序存储于索引数组中，第0号标记中记录满足最小支持度(Minsup)的数量。这就使1项集在结构树中的信息按设定的支持度阈值从高到低有序存储于索引数组。

最后，构建FP-tree算法的In条件模式树，通过遍历In后缀路径对数组a[0]进行判断，看a[0]是否在树中存在对应节点，存在计入数组中，否则存储为0。当扫描结束后，项目In的条件模式树也就建成了。

采用此方法建树及其查找频繁项集，极大地节省了空间开销，提高了建树和查找频繁项集的效率。算法伪代码如下：

Input: constructed FP-tree of according to A database, and a min-sup ξ

Output: maximal frequent item sets(MFIS)

Method: improved FP- tree (FP-tree, α)

Procedure improved FP- tree (FP- tree, α)

{

1)if FP- tree only contains a path of single prex

2)then{

3)generate candidate of maximal frequent item sets β∪α, adjusted item;

4)If β∪α is not a subset of the maximal frequent item sets in MFIS;

5)Then MFIS=MFIS ∪β ∪α;

6)}

7)else{

8)to find nodes from nodes support≥min-sup ξ longest continuous path, record the corresponding item number in a header table as N0;

9)for(N=index array[0]; N≥N0;N--){

10)generate pattern β=an∪α and support=support(an);

11)use improved method of this paper to construct β’s conditional FP-tree Treeβ;

12)if Treeβ≠Ø

13)then call FP-tree(Treeβ, β);

14)Else{

15)If β is not a subset of MFIS that already has the largest number of frequent item sets;

16)Then MFIS=MFIS∪β;

例11 标准状况下,往100 mL0.2mol·L-1的FeBr2溶液中通入一定体积的Cl2,充分反应后,溶液中有50%的Br-被氧化。则通入的氯气的体积是( )。

17)}

18)}

19)}

2 案例分析

以旅游大省云南省为例，从旅游网站采集数据，通过算法来挖掘游客最喜欢的旅游线路，优化配置旅游市场资源，同时用于旅游行业的各项判断，寻找更好的商业契机。

2.1 算法比较分析

旅游信息系统中，在数据库D中有海量数据信息，本文通过表1和表2的数据进行算法分析。

表1 旅游目的地

项目编号项目I1昆明I2大理I3丽江I4香格里拉I5西双版纳

表2 旅游网数据库中用户兴趣地调查

TID用户希望旅游城市01I1，I2，I302I2，I3，I403I1，I504I1，I2，I3，I405I2，I306I1，I4，I507I1，I2，I3，I508I2I3I509I1I2I5

将表2的信息用邻接矩阵存储用户希望旅游城市之间的关系。如表3所示。

表3 邻接矩阵存储频繁1，2-项集

I1I2I3I4I5I164324I247623I336622I422231I543215

通过表3中的数据很容易搜索产生频繁1-项集和2-项集：

1)产生频繁1-项集。表3中邻接矩阵对角线上{Ii，Ii}对应的值就是1-项集的支持度，如表4所示。

表4 1-项集支持度表

项集支持度I16I27I36I43I55

2)频繁2-项集的挖掘。挖掘频繁2-项集{Ii,Ij}，只需要扫描邻接矩阵表中第i行和第j列对应数值，如表5所示。

表5 2-项集支持度表

根据产生FP-tree树[12-13]的2个步骤来建立本文案例树：

根据支持度数据表(表6)，构建FP-tree树(图1)，寻路共用相同前缀路径。

表6 支持度有序表

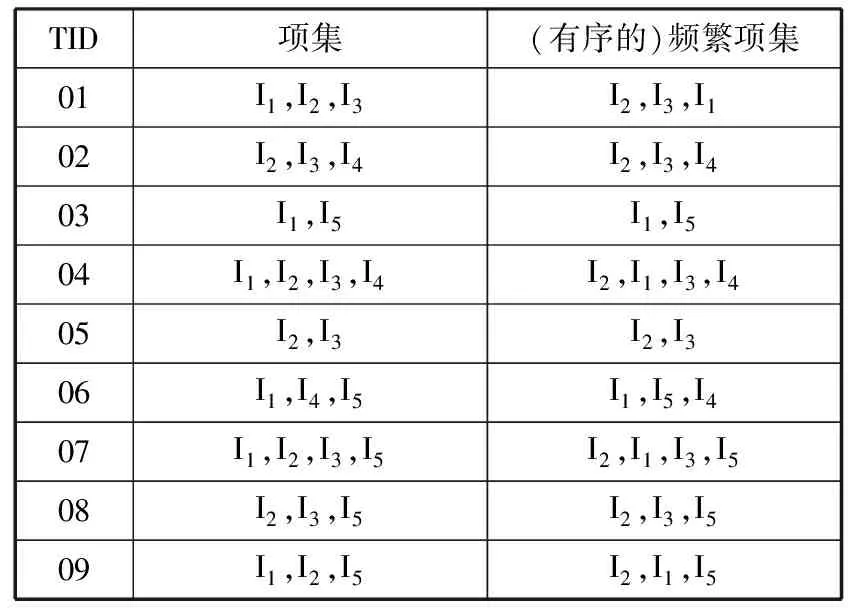
TID项集(有序的)频繁项集01I1，I2，I3I2，I3，I102I2，I3，I4I2，I3，I403I1，I5I1，I504I1，I2，I3，I4I2，I1，I3，I405I2，I3I2，I306I1，I4，I5I1，I5，I407I1，I2，I3，I5I2，I1，I3，I508I2，I3，I5I2，I3，I509I1，I2，I5I2，I1，I5

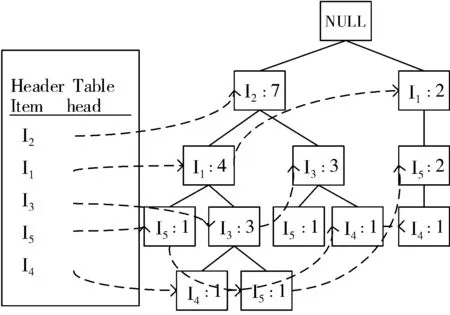
图1 构建FP-tree树

通过逆序HT(Header Table)表中的项，产生每个项的条件模式基(表7)，应用HT表中的项，逆寻遍历结构树找出对应项的全部前缀路径，该项(item)的条件模式基(CPB)就是这些前缀路径，该前缀路径上项(item)的频繁度为这些条件模式基(CPB)的频繁度构成。如图1构建的FP-tree树中，包含I4的其中一条路径是I2I1I3，该路径中I4的频繁度为1，则该CPB I2I1I3的频繁度为1。

表7 条件模式基

项集条件模式基I4I2I1I3：1， I2I3：1I5I2I1：1， I2I1I3I5：1， I2I3：1， I1：2I3I2I1：3， I2：3I1I2：4I2NULL

构造条件FP-tree(conditional FP-tree)。通过累加每个条件模式基(CPB)上的项(item)的频繁度，去除低于阈值的项(item)，从而构建FP-tree树。从而很容易在FP-tree树中得到频繁3-项集{Ii,Ij,Ik}或者更高频繁项集。通过设置的最小支持度在已构建的FP-tree中寻路获取频繁项集(图2)。

图2 挖掘频繁3-项集

假设设置最小支持度为3，则3-项集{I1，I2，I3}为最终频繁项集，对于N-项集不再为所需项集。改进后的算法，不但极大减少了频繁项集量，且对存储空间也是一个极大的释放，在计算支持度时，只需要扫描部分邻接矩阵和所构建FP-tree树。

然而，当挖掘对象为旅游网站的海量数据且支持度较小时，会产生大量频繁项集，内存开销很大。这时，可以通过索引改进方法弥补这一缺陷。

下面是挖掘项目I3为后缀的最大频繁集实验算法步骤。设置最小支持度为3。对2个数据结构数组初始值设为0，对I3为后缀的分支进行逆寻遍历并对数组做对应的更新，更新后支持度数组如图3所示。

063

图3 I3条件模式基中的支持度

满足最小支持度为3的支持度数组为[1]=6，[2]=3，这样让数组下标1，2存入索引数组中，如图4所示。

212

图4 索引数组

再对I3为后缀的路径进行逆寻遍历，抽取首次遍历的路径，把结构树中的节点信息存储于支持度数组中，如图5所示。

012

图5 取出路径(I2,I1)后的支持度数组

因此，以I3为后缀的最大频繁集为{I2,I1,I3}:3。以同样的方法挖掘以I5为后缀的最大频繁集所得{I1,I5}:4，以I1为后缀的最大频繁项目集{I2,I1}:4为已存在最大频繁项集的子集，故抛弃，其他为不满足最小支持度。至此本算法的挖掘过程结束，挖掘结果和FP-Growth算法挖掘结果相同。这一改进可以大大减小数据存储的内存开销以及提高执行效率。

优化算法的同时也需要得到精准的关联规则，当可信度和支持度挖掘出的关联规则完全无法满足游客对于旅行线路规划的判断时，引入了一个新的标准：通过兴趣度来更精准判定强关联规则。

兴趣度[14]的主要思想就是：通过支持度-置信度模式，若P(B|A)与P(B)的概率比较后相差较大，可以表明A的存在对B的存在影响很大，规则A=>B兴趣度很高，这也将给用户的各种选择及决策过程提供有意义的指导信息。以下为基于概率差值的兴趣度定义:

Interest(A->B)=P(B|A)-P(B)

Interest(A->B)的度量有2种可能的情况：

1)如果Interest>0，那么A和B正相关；

2)如果Interest<0，那么A和B负相关。

以表1中的数据作一个分析“去昆明(I1)-去大理、丽江(I2，I3)”其兴趣度为：

Interest(I1->I2，I3)=P(I2，I3|I1)-P(I2，I3)=1/3

由此得出，该规则体和结论是正相关的，反映正相关的规则体“去昆明(I1)-去大理、丽江(I2，I3)”应该加大投入。

2.2 实验结果与分析

对改进算法性能的分析评估是以Windows 7操作系统作为实验支撑，相关配置为Inter(R) Pentium CPU G2303主频3.00 GHz，4 GB内存，通过C++语言来实现。样本数据来源于UCI旅游数据集，抽取数据集中5672条记录。将改进算法与经典FP-Growth算法及Apriori算法进行比较，实验结果分析表明，改进算法数据挖掘效率明显优于FP-Growth算法及Apriori算法，算法比较分析如图6所示。

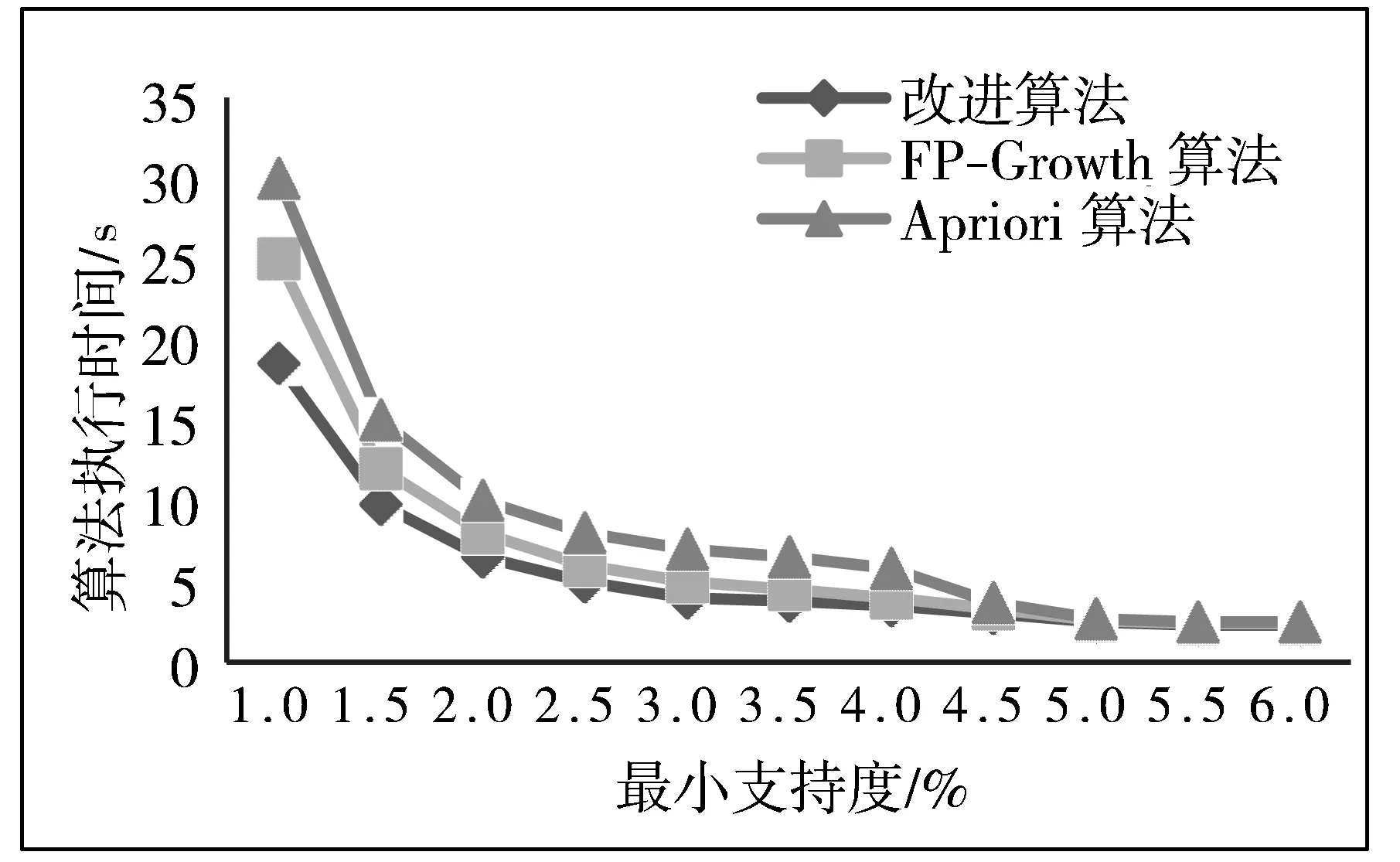
图6 算法执行效率比较

根据实验结果分析得到，面对海量数据，当最小支持度为1.0%时，改进算法的执行时间要比FP-Growth算法减少约38%，比Apriori算法减少约67%，表明当挖掘对象为海量数据且支持度越小时改进算法的高效性。然而当设定最小支持度≥4.5%时，遍历迭代次数急剧减少，所以这几种算法的执行效率相差从0.01%趋于0。

2.3 旅游线路规划中数据挖掘的结构性系统设计

基于数据挖掘技术在旅游市场及线路规划系统的在线模块[15]，能够为用户提供在线浏览最受欢迎的旅游线路，同时为商家提供游客最喜欢的线路，以便做好更好的服务和获得最大的收益。在线模块的具体结构如图7所示。

图7 系统体系结构

数据挖掘技术中的关联规则模块是通过对数据的清理、转换以及应用加载工具对初始数据库D的数据抽取，同时获得标准数据，对深入挖掘海量数据有极大的帮助。对于数据挖掘中的关联规则挖掘实施，可以通过对Apriori算法与FP-tree算法进行叠加，然后通过对已挖掘关联规则分析后写入规则库中。

旅游线路规划推荐模块让消费者通过Web或者APP来访问，后台数据库会通过大数据平台记录用户的访问信息，这样数据库记录生成相关联的数据，当网站浏览者不知如何规划旅游热线的时候，不需要用户更多的信息，即可为用户提出多条相关的旅游热线和游客最热衷的旅游热线，用户也不用担心个人信息的泄漏。这些体现了关联规则在旅游线路推荐系统中的智能[16]化特点。应用这一智能模块，系统可以存储消费者访问过程中搜索旅游线路的频繁数据，然后反馈到推荐模块，最后系统通过分析和预处理将以一定形式把处理好的数据推荐给用户，反馈数据以一定的形式返回给系统，从而实现旅游线路推荐的目的。

3 结束语

本文描述了数据挖掘FP-Growth算法及其相关改进，并且把基于关联规则挖掘技术应用到旅游线路挖掘中，挖掘最受游客喜爱的旅游线路。对旅游信息系统中的数据通过使用FP-tree算法及改进后的算法结果进行比较分析，表明改进后的建树方法提高了建树的效率、减少了内存开销同时也提高了查找效率，结果分析验证了改进后的FP-Growth算法的有效性。改进后的算法有着比较明显的优势，对于海量的用户数据存储和细化旅游线路执行效率有了更好的提高，这也可以更好地挖掘出消费者喜爱的旅游线路、目的地等重要信息，挖掘结果对旅游线路的设计及规划有重要的指导意义。但由于数据挖掘技术很多算法都是基于“支持度(support)-置信度(confidence)”这一框架，这样的模式结构同时也容易挖掘出精确度低或错误的数据规则，所以怎样使用户的极大需求和系统的高效性相结合，后续需要做更多的研究应用。

[1] Agrawal R, Imielinski T, Sami A． Mining association rules between sets of items in large database[C]// Proceedings of 1993 ACM SIGMOD International Conference on Management of Data. 1993:207-216．

[2] 马盈仓． 挖掘关联规则中Apriori算法的改进[J]． 计算机应用与软件， 2004,21(11):82-84．

[3] 刘娟,宋安军. 改进FP-Growth算法在气象预报中的应用[J]. 计算机系统应用, 2016,25(10):199-204.

[4] 廖友金. 基于有向图的关联规则挖掘研究与改进[D]. 南京:东南大学, 2015.

[5] 晏杰,亓文娟. 基于Aprior & FP-Growth算法的研究[J]. 计算机系统应用, 2013,22(5):122-125.

[6] 周茂恩,柳虹. Apriori和FP-Growth算法在软考数据分析中的应用[C]// 2010 International Conference on Management Science and Engineering. 2010:225-228.

[7] 纪怀猛. 基于改进FP-Tree的最大频繁项集高效挖掘算法[J]. 计算机与数字工程， 2014,42(6):959-963.

[8] 杨云,罗艳霞. FP-Growth算法的改进[J]. 计算机工程与设计, 2010,31(7):1506-1509.

[9] 黄剑,李明奇,郭文强. 并行FP-Growth算法在搜索引擎中的应用[J]. 计算机科学, 2015,42(S1):459-461.

[10] 侯长满,余彪. 关联规则算法FP-Growth的研究与分析[J]. 计算机与网络， 2016,42(24):58-61.

[11] 迟丽宁. 基于FP-Growth的分类规则挖掘算法及其应用[D]. 青岛:青岛大学, 2012.

[12] 刘喜苹. 基于FP-Growth算法的关联规则挖掘算法研究和应用[D]. 长沙:湖南大学, 2006.

[13] 李志云,周国祥. 基于FP-Growth的关联规则挖掘算法研究[C]// 全国第18届计算机技术与应用(CACIS)学术会议. 2007:204-206.

[14] 李伟东,倪志伟,刘晓． 基于兴趣度的关联规则挖掘[J]． 计算机技术与发展, 2007,17(6):80-82.

[15] 吴春阳,何友全. 数据挖掘技术及其在旅游线路规划系统的应用[J]. 计算机技术与发展, 2008，18(9):235-238.

[16] 朱全,廖光忠. 基于加权关联规则的智慧旅游推荐系统[J]． 工业控制计算机， 2014(9):116-118．