传输损耗条件下基于循环平稳检测的空时分组码盲识别方法

方 伟，闫文君，凌 青,张立民

(海军航空工程学院信息融合研究所,山东 烟台 264001)

0 引 言

非合作条件下的信号盲识别是现阶段研究的热点问题，其在军事领域还是民用领域应用都较为广泛，其中信号识别的一个新的重要研究方向就是空时分组码(Space-Time Block Code, STBC)盲识别问题[1]。

STBC是充分利用多天线系统进行传播的有效手段[2]，大大提高了无线通信的有效性和可靠性。多输入多输出(Multiple Input Multiple Output, MIMO)系统和STBC的结合是一项有前途的技术，这使得STBC的盲识别尤为关键[3]。现阶段主流的STBC盲识别方法主要有最大似然法[4]、二阶相关矩阵法[5]、高阶累积量[6-8]和循环平稳法[9-10]等。其中最大似然法能够给出正确识别概率的最优解，其识别效果在目前是最理想的，然而其识别之前需要预先知道信道信息、噪声信息和调制信息，且计算复杂度较高[4]。

上述的大部分算法都是在MIMO条件下进行识别[4-6,9-10]的，然而由于接收端功率或成本等因素限制，单接收天线是必然存在的情况，这就出现了专门研究单接收天线下STBC识别的算法[7-8,11]。

多接收天线下算法由于接收信号为矩阵信号，可以较为容易地依据空时分组码正交特性进行识别，而单接收天线的接收信号为非矩阵信号，无法利用空时分组码正交特性进行识别，因此许多算法多天线下能用，而单天线下不能用。单天线下算法主要考虑空时分组码矩阵内信号的相关特性作为特征参数，不仅适用于单接收天线，还适用于多接收天线下。基于正交特性识别的算法较为简单，基于相关特性识别的算法较为复杂。

同时，传输损耗是空时分组码盲识别中不可避免的问题，在传输损耗条件下，由于时延、相位和频率的偏移，其正交特性不再显著，传统的检测算法在低信噪比下不再适用。在上述算法中，只有文献[9]研究了传输损耗条件下的识别方法，该文献建立了空时分组码信号的传输损耗模型，使用基于二阶循环平稳的算法进行盲识别。然而，该算法不适用于单接收天线条件。

本文同时考虑单接收天线和传输损耗的条件，采用基于四阶循环平稳[12]的算法对空时分组码进行盲识别研究(按照惯例，研究对象为SM和Alamouti STBC)，本文算法有如下优点：

1)采用了传输损耗条件下STBC盲识别；

2)可在单接收天线下进行识别；

3)不需要预先知道信道信息、调制方式、载波相位和时间偏移，不需要精确知道载波频偏。

1 信号模型

考虑具有nt个发射天线，1个接收天线的无线通信系统。定义每组STBC需要传输的符号数为K，需传输的时隙为L，则STBC码矩阵的维数为nt×L，该STBC码矩阵传输的符号S=[s1,…，sK]。定义第b个传输块生成的编码矩阵为Cλ(Sb)，λ为编码矩阵类型，第b个传输块Xb=[sb,0,sb,1,…,sb,K-1]。

本文对SM和Alamouti STBC进行识别。SM码矩阵为：

CSM=[s1s2… snt]T

Alamouti码矩阵为[2]：

引入两发射天线系统，接收信号r(t)表示为：

r(t)=yλ(t)ej2π(Δfct+φ0+φ(t))+v(t)

(1)

式(1)中，Δfc是载波频偏；φ0是载波相位偏差；φ(t)是载波相位噪声；v(t)是零均值的高斯白噪声；yλ(t)是接收信号,其中λ∈{SM,AL}。y(t)可表示为：

(2)

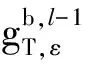
通过计算接收信号的四阶循环平稳，找出SM和Alamouti STBC不同的循环频率，以此作为特征参数。为此，作如下假设：

3)噪声是不相关的，即E[vi(t)vj(t+τ)]=0。

上述假设中i,j表示不同的符号(或噪声)的序号。

本文的目标是从接收信号中提取不同STBC的不同特征参数，从而进行STBC的识别。

2 四阶循环平稳

2.1 四阶循环累积量

接收信号r(t)的i阶循环矩Mi(α；τ)可以用四阶时变矩mi(t；τ)的傅里叶变换表示[13-14]：

mi(t;τ)=E[r(t)r(t+τ1)…r(t+τi-1)]

(3)

(4)

其中，α代表循环频率。

同样地，时变累积量ci(t;τ)可以用循环累积量Fi(α;τ)的傅里叶级数表示：

(5)

(6)

其中，Α是Fi(α;τ)≠0的循环频率的集合。

根据四阶循环累积量定义[15]：

F4(α,τ1,τ2,τ3)=M4(α,τ1,τ2,τ3)-

M2(α-β;τ2)M2(β;τ1-τ3)ejβτ3+

M2(α-β;τ3)M2(β;τ2-τ1)ejβτ1

(7)

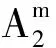
F4(α,τ1,τ2,τ3)=M4(α,τ1,τ2,τ3)

(8)

2.2 SM码的循环频率

由公式(1)、公式(2)和假设条件1，SM的四阶累积量为：

cSM(t,τ)=E[r(t)r(t+τ1)r(t+τ2)r(t+τ3)]=0

(9)

其中，延迟参数τi取任意数。由于SM不同的符号之间相互独立，因此不同的接收信号是相互独立的，即SM没有任何循环频率。

2.3 Alamouti STBC的循环频率

设τ2=0，τ1=τ3=τ，Alamouti STBC的四阶累积量表示为：

cAl(t,τ)=E[r(t)r(t+τ1)r(t+τ2)r(t+τ3)]

=E[yy(t)yy(t+τ)yy(t)yy(t+τ)]

=a(t,τ)b(t,τ)

(10)

式(10)中：yy(t)=yλ(t)ej2π(Δfct+φ0+φ(t))，且

(11)

(12)

θ(t,τ)=8πΔfct+4πΔfcτ+8φ0+4φ(t)+4φ(t+τ)

(13)

由式(12)可以观察到cAl(t,τ)是周期为2T的周期函数，对式(10)进一步变形为：

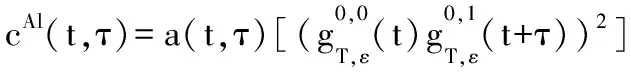
(14)

其中⊗表示克罗内克积，因此，cAl(t,τ)的傅里叶变换FAl(α,τ)可表示为：

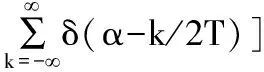
(15)

(16)

其中，A(α,τ)是a(t,τ)的傅立叶变换。如果A(α,τ)与α相互独立，显然可以得到FAl(α，τ)具有1/2T的整数倍的循环频率。

2.4 传输损耗的影响

在Alamouti STBC条件下，由式(15)可知，FAl(α,τ)由A(α,τ)和B(α,τ)的卷积组成。A(α,τ)对FAl(α,τ)只有乘积作用，包含的传输损耗因子有{h(t),Δfc,φ0,φ(t)}。由式(12)～式(16)可知：φ0会对FAl(α,τ)产生相位旋转，不会对循环频率的位置和幅度产生影响。而Δfc会使FAl(α,τ)的循环频率移动2Δfc，同时会产生相位旋转。φ(t)和h(t)会改变FAl(α,τ)幅度和相位，而且还会产生新的频率成分。B(α,τ)包含的传输损耗因子只有ε，而ε只改变FAl(α,τ)的相位，不会改变幅度。

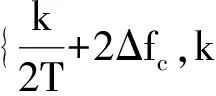
综上所述：

1)SM码FSM(α,τ)没有任何的循环频率；

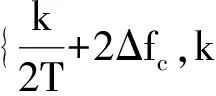
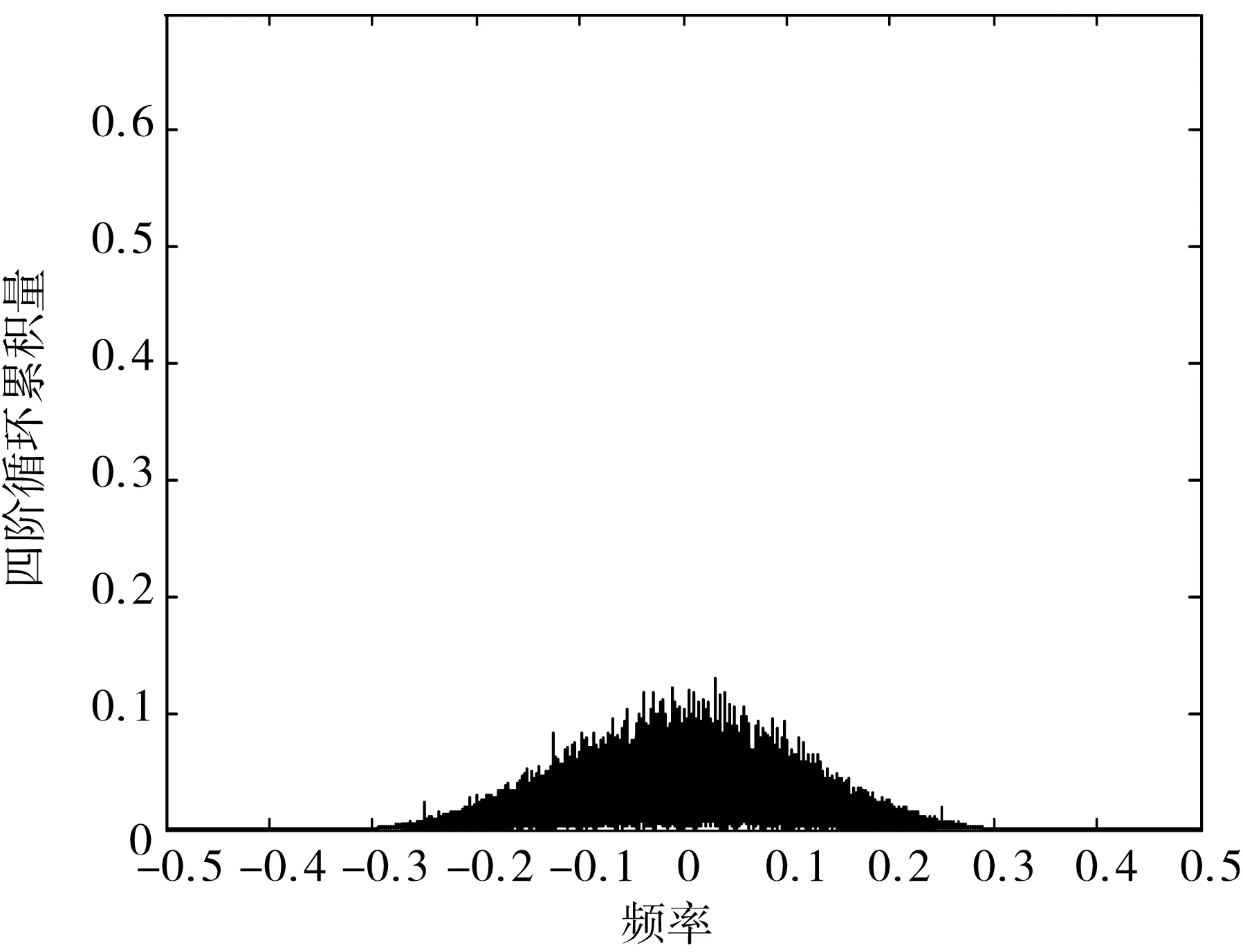
图1 SM的四阶循环累积量

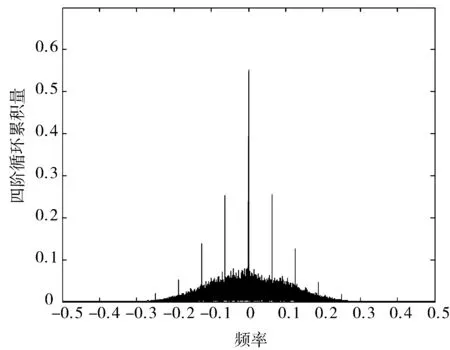
图2 Alamouti码的四阶循环累积量

3 循环平稳检测

由算法的流程可知，判定码型的分类，需要检测是否存在循环频率，循环频率的存在性检测通过循环平稳检测完成[12]。

假定α是任意一个待检测的循环频率，τ1,…,τIτ是时延，Iτ为时延的个数，接收信号四阶累积量估计值为：

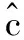
(17)

c4≜[Re {c4(α,τ1)},…,Re {c4(α,τIτ)},

Im {c4(α,τ1)},…,Im {c4(α,τIτ)}]

(18)

检验α是否为待检测的循环频率，假设检验为：

(19)

其中，A4是四阶循环频率的集合；ξ4为估计的错误向量，当接收信号时隙数N→，ξ4趋于零。

(20)

构造统计量T4如下：

(21)

(22)

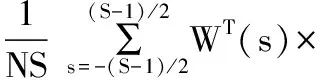
(23)

(24)

其中，m,n=1,…,Iτ，此处取时延τ=±T，因此Iτ=2。

(25)

式(23)、式(24)中，WT是长度为S的频谱窗，S为奇数。

在假定条件H0下，T4服从自由度为2Iτ的卡方分布。设定阈值Γ对假设检验进行判决分析，若T4≥Γ认为假设H1成立。则有：

(26)

虚警概率公式为Pfa=1-P(T4<Γ)，则阈值Γ可表示为：

Γ=-2ln (1-(1-Pfa)N)

(27)

4 仿真和结果分析

4.1 算法流程

1)在时延向量τ=(0,P,0,P)下计算接收信号的四阶循环累积量FAl(α,τ)；

3)根据公式(22)～公式(25)计算Σ4；

4)根据公式(21)计算统计量T4；

5)构造自由度为2Iτ的卡方分布，根据公式(26)求取阈值Γ；

6)判断α在时延τ=±T下是否是FAl(α,τ)的循环频率：若T4≥Γ认为α是循环频率，判定接收信号为Alamouti码，否则认为不是循环频率，判定接收信号为SM。

4.2 算法仿真

算法经过1000次蒙特卡洛仿真，频谱整形采用滚降系数为0.35的升余弦滤波器，过采样系数P=8，接收端采用13阶巴特沃斯低通滤波器，噪声为零均值高斯白噪声，信噪比范围为-10 dB～20 dB，信噪比计算公式为10log10(nt/σ2)，公式(23)和公式(24)中频谱窗WT采用长度为S=0.06N的凯泽窗，其整形参数为10。发射滤波器和接收滤波器的时延ε和载波相位偏差φ0分别取分布为[0,T)和[0,2π)的随机数，载波频偏Δfc=0.04/T。在上述条件下，若观察到的接收符号数Ns=1024，则接收端接收到的采样信号数为Ns×P=1024×8=8192。信道采用平坦衰落的瑞利信道，载波相位噪声φ(t)初始值设为0。正确识别概率公式定义为：P(λ|λ)，其中λ∈{SM,AL}。

4.2.1 不同接收信号数对识别性能的影响

仿真条件为信号采用QPSK调制方式进行调制，四阶累积量的时延τ=(0,P,0,P)，采用QPSK的调制方式，虚警概率Pf=0.001，接收符号数Ns分别为256,512,1024,2048和4096。

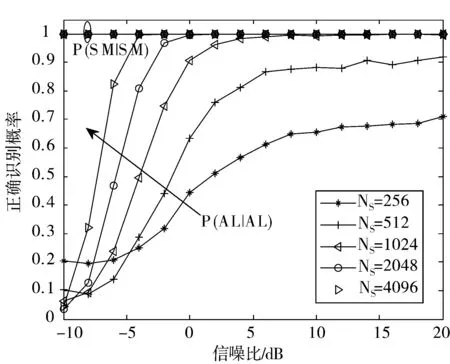
图3 不同接收符号数下的正确识别概率

仿真结果如图3所示。在较低的接收符号数下(256,512)，Alamouti码的识别误差较大，在较高的接收符号数下，Alamouti的识别效果较好。由于SM不具有循环频率，不同的接收符号数对于SM的识别没有影响。

4.2.2 不同虚警概率对识别性能的影响

仿真条件为信号采用QPSK调制方式进行调制，四阶累积量的时延τ=(0,P,0,P)，采用QPSK的调制方式，接收符号数Ns=1024，虚警概率Pf分别取0.0001,0.001和0.01。

仿真结果如图4所示。可以看出，随着虚警概率的增大，Alamouti码的识别能适应更低的信噪比，在低信噪比下，噪声会加大估计误差，较大的虚警概率改变了阈值，使得Alamouti的识别效果更好。对于SM码的识别，较大的识别概率减小了其正确识别概率，很显然，阈值的增大会影响到SM的正确识别。

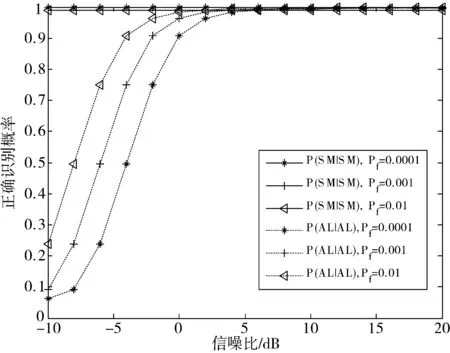
图4 不同虚警概率下正确识别概率

4.2.3 不同调制方式对识别性能的影响

仿真条件为信号分别采用QPSK、8PSK、16QAM和64QAM方式调制，虚警概率Pf=0.001，信号四阶累积量的时延τ=(0,P,0,P)，接收符号数Ns=1024。

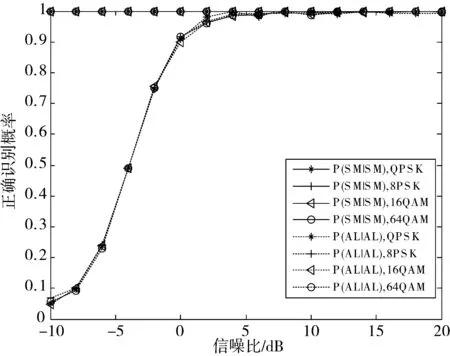
图5 不同调制方式下正确识别概率

仿真结果如图5所示，可以看出，本文算法对调制方式不敏感，不需要预先估计(或知道)传输信号的调制方式。

4.2.4 相位噪声和多普勒频移对识别性能的影响

仿真条件为信号采用QPSK调制，虚警概率Pf=0.001，信噪比为10 dB，信号四阶累积量的时延τ=(0,P,0,P)，接收符号数Ns=1024。定义相位噪声为偏移率为βT的维纳过程[16]，采用改进JAKES模型作为时变信道模型[17]。

仿真结果如图6所示，随着βT和fdT(fd为最大多普勒频移)变大，Alamouti码的识别效果变差，可以看出，为保证算法识别性能，应取βT0.001且fdT0.001。相位噪声和多普勒频移对SM没有影响。

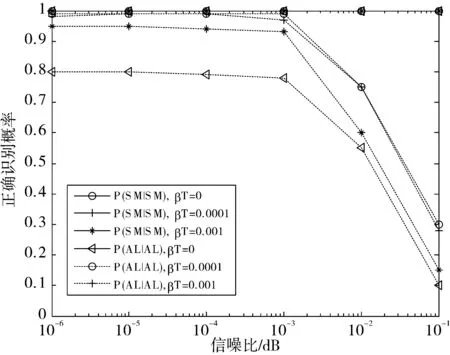
图6 不同相位噪声和多普勒频移下正确识别概率

4.2.5 不同算法识别性能的影响

本文选取2种研究单接收天线下STBC识别的文献进行比较[5,11],这2种算法均没有考虑传输损耗对识别算法的影响；同时选择仅有的1种研究传输损耗条件下的识别问题的算法进行性能比较[9]。其中文献[5]采用了基于FOLP的算法(FOLP)，文献[11]采用了基于K-S检测的算法(KS)，文献[9]采用了基于二阶循环平稳的算法(SC)。

仿真条件：信号分别采用QPSK调制，虚警概率Pf=0.001，信号四阶累积量的时延τ=(0,P,0,P)，接收符号数Ns=2048。

仿真结果如图7所示。可以看出，本文算法(PM，Proposed Method)对于Alamouti码的正确识别概率在-2dB时达到1。尽管PM考虑了传输损耗，算法性能依然优于其他2种未考虑传输损耗的算法[4,10]，PM性能比FOLP和KS的性能平均提高了2 dB左右。与考虑了2根接收天线且包含了传输损耗的算法相比[9]，算法性能提高了6 dB左右。PM优于FLOP、KS和SC。同时反映出，四阶循环平稳算法不仅适用于单接收天线条件下，在性能上也要优于二阶循环平稳算法，且两者的计算复杂度均为O(Nslog Ns)。

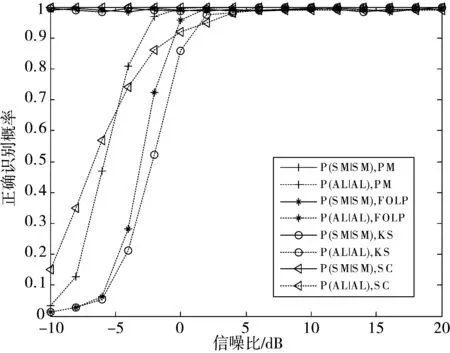
图7 不同算法正确识别概率

5 结束语

本文在单接收天线下，研究了传输损耗条件下空时分组码的识别问题，设计了基于四阶循环平稳的空时分组码识别算法，给出了实现流程和仿真结果。识别算法不需要知道调制信息、噪声信息、信道信息、载波相位和时延，也不需要确切知道载波频偏，算法对相位噪声和多普勒频移具有很好的适应性。与现有的单接收天线下没有考虑传输损耗的识别算法相比，本文算法在低信噪比下表现出更好的识别性能，算法性能提高了约2 dB；与现有的两接收天线且考虑了传输损耗的算法相比，本文算法性能大约提高了6 dB。

[1] 闫文君,张立民,凌青,等. 空时分组码盲识别技术综述[J]. 计算机与现代化, 2015(9):66-71.

[2] Alamouti S M. A simple transmit diversity technique for wireless communication[J]. IEEE Journal on Selected Areas in Communication, 1998,16(8):1451-1458.

[3] Marey M, Dobre O A. Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J]. IEEE Signal Processing Letters, 2014,21(9):1098-1102.

[4] Choqueuse V, Mazarin M, Collin L, et al. Blind recognition of linear space time block codes: A likelihood-based approach[J]. IEEE Transactions on Signal Processing, 2010,58(3):1290-1299.

[5] Eldemerdash Y A, Dobre O A, Liao B J. Blind identification of SM and Alamouti STBC-OFDM signals[J]. IEEE Transactions on Wireless Communications, 2015，14(2):972-982.

[6] 张立民,闫文君,凌青,等. 一种单接收天线下的空时分组码识别方法[J]. 电子与信息学报, 2015,37(11):2621-2627.

[7] Yan Wenjun, Zhang Limin, Ling Qing. An algorithm for space-time block code classification using higher-order statistics (HOS)[J]. Springer Plus, 2016,5(1):1-13.

[8] 闫文君,张立民,凌青,等. 基于高阶统计特征的空时分组码盲识别方法[J]. 电子与信息学报, 2016,38(3):668-673.

[9] Marey M, Dobre O A, Inkol R. Classification of space time block codes based on second-order cyclostationarity with transmission impairments[J]. IEEE Transactions on Wireless Communication, 2012,11(7):2574-2584.

[10] Karami E, Dobre O A. Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity[J]. IEEE Transactions on Vehicular Technology, 2015,64(3):942-953.

[11] Mohammadkarimi M, Dobre O A. Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov(K-S) test[J]. IEEE Communications Letters, 2014,18(10):1711-1714.

[12] Dandawate A V, Giannakis G B. Statistical test for presence of cyclostationarity[J]. IEEE Transactions on Signal Processing, 1994,42(9):2355-2359.

[13] Gardner W, Spooner C. The cumulants theory of cyclostationarity time-series, Part I: Foundation[J]. IEEE Transactions on Signal Processing, 1994,42(12):3387-3408.

[14] Serpedin E, Panduru F, Sari I, et al. Bibliography on cyclostationarity[J]. Signal Processing, 2005,85(12):2234-2303.

[15] 张贤达. 信号分析与处理[M]. 北京：清华大学出版社， 2011.

[16] Demir A, Mehrotra A, Roychowdhury A. Phase noise in oscillators: A unifying theory and numerical methods for characterization[J]. IEEE Transactions on Circuits and Systems, 2000,47(5):655-674.

[17] Zheng Yahong, Xiao Chengshan. Simulation models with correct statistical properties for Rayleigh fading channels[J]. IEEE Transactions on Communications, 2003,51(6):920-928.