精密复杂零件数控加工在线检测与误差补偿技术研究*

毛文亮，杨小平

(1.甘肃机电职业技术学院，甘肃 天水 741001； 2.甘肃农业大学 科研处，甘肃 兰州 730000)

0 引 言

航空发动机叶片、大型舰船螺旋桨、高精密模具等复杂零件制造是一个国家制造业水平的集中体现。随着我国数控技术的飞速发展，对精密复杂零件数控加工检测技术提出了更高要求。虽然三坐标测量机的出现大大提高了检测精度，但由于存在二次装夹定位误差和尺寸受限等缺点，无法得到广泛应用。近年国内许多学者对在线检测系统进行了深入研究，马云辉等[1]利用数控机床和加工中心上的位置检测系统实现了工件线性尺寸、孔、柱的测量；刘利剑等[2]用VB6.0编制的测量软件完成了长度、角度、位置度、形状度的自动测量。国外在线检测技术发展较快，CHO等[3]开发了轮廓铣削在线检测系统；T.R.Kramer等[4]用软件生成的DMIS格式文件,可直接在机床上完成从加工到检测全过程,并实时反馈加工。与国外相比，我国在线检测系统功能相对单一，对复杂曲面零件的在线检测系统开发较少，如何实现精密复杂零件数控加工“加工-测量-补偿加工”的闭环制造，是我国数字化制造中亟需解决的一项重要课题。

1 数控加工在线检测及误差补偿原理

将测头安装在数控机床刀库中，跟加工工件一样，数控机床从刀库调出测头，由程序控制测头自动测量，将测量结果反馈给数控机床控制系统，数控系统将此时的测球中心坐标通过串行通讯接口传输给计算机，利用检测软件对测量结果进行分析，并进行误差补偿，精密复杂零件数控加工在线检测及误差补偿原理如图1所示。

2 确定性复杂曲面回归模型的建立

将测点数据的确定性复杂曲面定义在 CAD 系统中，用A(u,v)表示实际加工曲面，B(u,v)表示理想复杂曲面，ds(u,v)表示复杂零件数控加工的系统误差，dr(u,v)表示复杂零件数控加工的随机误差，u、v表示两个参数，则：

A(u,v)=B(u,v)+ds(u,v)+dr(u,v)

(1)

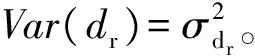
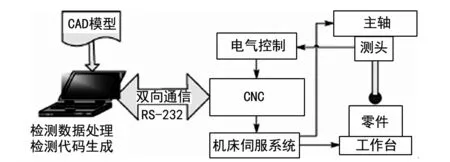
图1 精密复杂零件数控加工在线检测及误差补偿原理

用双三次B样条曲面描述确定性曲面模型，在空间给定(n+1)(m+1)个点Gij(i=0,1,…,n;j=0,1,…,m)，可逼近生成一个n×m次的 Bézier曲面片，多个三次B样条曲面片的表达式为[5]：

(2)

式中:Ui(u)和Vj(v)为B样条基函数；Rij为控制点，曲面片的数量为h×l。控制点与基函数张量积的线性组合就是曲面模型。因此，式(2)可表示为[5]：

(3)

式中:Xk为B样条基函数的张量积；Rk=(xrk,yrk,zrk)T为相应的控制点；F=(h+3)(l+3)为控制点的数量。

设Pw(w=0,1,…,z)为实际曲面z个测点的坐标，矩阵X为每个测点相关的张量积，则确定性曲面控制点的线性回归模型可表示为[6]：

P=XR

(4)

最小二乘估计值为：

(5)

(6)

由于零件表面上加工误差远小于零件尺寸，所以，回归模型测点的u、v参数可以用检测时的理想曲面参数u、v代替，确定性曲面的估计回归模型可表示为[6]：

(7)

残差可表示为：

(8)

3 加工误差分解

(9)

(10)

式中:ωij表示在位置点i处，位置j对它的空间作用的度量权重系数。检验统计量可表示为：

(11)

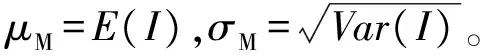
(12)

对确定性曲面回归分析模型进行迭代求取，采用单侧检验。取显著性水平为0.01，其标准正态分布的临界值T0.01的值则为2.33[7]，如果TT0.01，要重新建立回归模型进行检验统计，直到取样点法向残余偏差服从空间独立分布，把误差分解为系统误差和随机误差为止。

4 在线检测系统误差补偿

根据精密复杂零件数控加工系统误差与补偿点之间的补偿量关系，建立补偿点计算数学模型，公式(13)为补偿点的计算公式[7]：

(13)

根据补偿点公式计算结果，修改NC代码，将理想曲面刀具路径偏移一个系统误差值，生成新的刀具路径，重新走刀加工，即可实现曲面加工误差补偿。

5 试验验证

为验证有效性，采用 FANUC 0i VMC-850B三轴立式加工中心，TP60型触发式测头，对大量精密复杂零件数控加工进行了在线检测及误差补偿试验，并将试验零件在三坐标测量机上进行测量，结果显示，试验零件各项数据符合技术要求，与三坐标测量机测量结果基本一致，误差测头在线检测如图2所示，精密复杂零件数控加工补偿前后数据与CMM检测数据的对比如表1所示。

图2 误差测头在线检测

6 结 语

针对精密复杂零件数控加工在线检测及误差补偿中存在的问题，构建了基于B样条曲面的确定性曲面回归分析模型，通过空间独立性分析，将精密复杂零件的数控加工误差分解成系统误差和随机误差，通过补偿点偏差计算，修改数控加工程序，对系统误差进行了补偿，实现了精密复杂零件数控加工“加工-测量-补偿加工”的闭环制造，有效提高了精密复杂零件数控加工的精度。

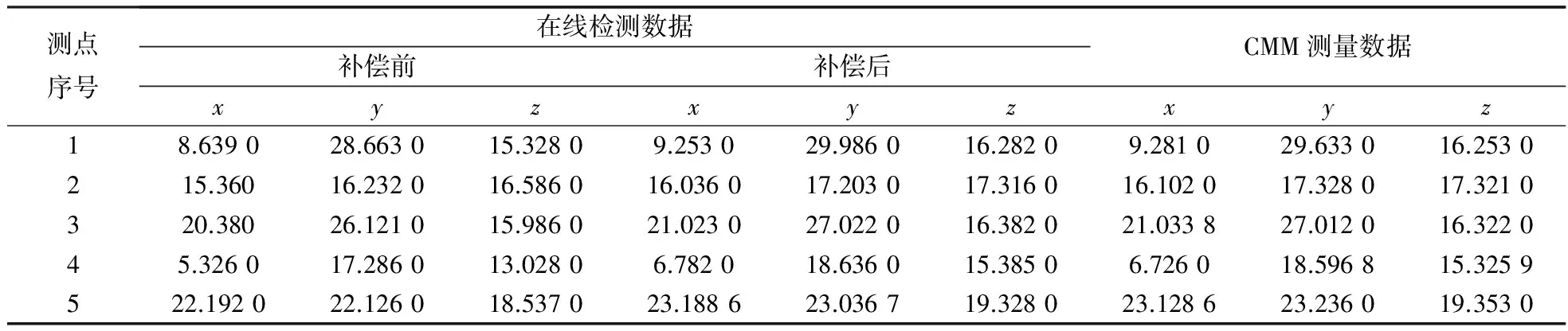
表1 精密复杂零件数控加工在线检测数据与CMM检测数据比较 /mm

[1] 马云辉.数控机床用在线检测系统的研究[J].组合机床与自动化加工技术,1990(8):45-47.

[2] 刘利剑.加工中心在线测量功能的实现[J].机械工程师,2002(12):501-504.

[3] Cho M W，Kim G H，Seo T I，et al. Integrated machining error compensation method using OMM data and modified PNN algorithm[J].International Journal of Machine Tools and Manufacture，2006，46(12-13)：1417-27.

[4] Kramer T.R. HH, Mession E., Proctor F.M., Scott H.A feature-based inspection and machining system[J].Computer-Aided Design, 2001, (33):653-669.

[5] Yan Z，Menq C H. Uncertainty analysis and variation reduction of three dimensional coordinate metrology，part 1： Geometric error decomposition[J].International Journal of Machine Tools and Manufacture，1999，39(8)：1199-1217.

[6] 陈岳坪，高 健，邓海祥，等.复杂曲面零件在线检测与误差补偿方法[J].机械工程学报，2012，48(23)：146.

[7] Yang B D，Meng C H. Compensation for form error of end-milled sculptured surfaces using discrete measurement data[J].International Journal of Machine Tools and Manufacture，1993，33(5)：725-740.